- 製造業出身のデータサイエンティストがお送りする記事
- 今回はscikit-learnを活用して様々な回帰モデルを実装し整理しました。
はじめに
今回は、機械学習の回帰モデルをscikit-learnを活用して実装してみました。
また、各手法を使用する際のポイントについても纏めてみました。
回帰モデル構築の一連の手順
回帰モデルを構築するにあたって一連の流れを下記に整理します。
各フェーズにおいて各々重要なことがありますが、詳細は別途整理します。
(1) 課題の整理 :解決すべきビジネス課題を明確にする
(2) データの収集 :入手可能なデータを整理し、目標達成が可能か評価する
(3) データの基礎集計 :分析するデータの特徴を可視化し、基礎集計を合わせて分析する
(4) データの前処理 :データに潜むゴミを取り除いてデータを綺麗にする
(5) 特徴量の抽出 :不要な特徴量を取り除いて必要な説明変数のみにする
(6) データの正規化 :特徴量のスケールを合わせるためにデータの正規化する
(7) 手法の選定 :データに合わせて適切な手法を選定する
(8) モデルの学習 :データの規則を選択した手法で学習する
(9) モデルの検証・評価:学習した手法の回帰精度を確認し、モデルの妥当性を評価する
scikit-learnについて
scikit-learnは、Pythonの機械学習ライブラリーです。
データの収集
今回はUCI Machine Learning Repositoryで公開されているボストン住宅の価格データを用いて予測モデルを構築します。
| 項目 | 概要 |
|---|---|
| データセット | ・boston house-price |
| サンプル数 | ・506個 |
| カラム数 | ・14個 |
pythonのコードは下記の通りです。
# 必要なライブラリーのインポート
import pandas as pd
import numpy as np
from sklearn.datasets import load_boston
# データセットの読込み
boston = load_boston()
# データフレームの作成
# 説明変数の格納
df = pd.DataFrame(boston.data, columns = boston.feature_names)
# 目的変数の追加
df['MEDV'] = boston.target
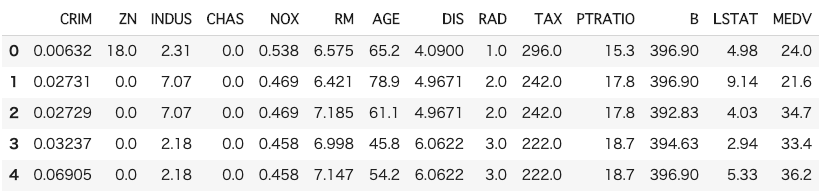
# データの中身を確認
df.head()
各カラム名の説明は省略します。
・説明変数:13個
・目的変数:1個(MEDV)
データの基礎集計
今回、説明変数が13個ありますので、効率的に各説明変数や目的変数間の関係を見るために多変量連関図を用います。
今回はseabornというライブラリーを活用して可視化を行ってみたいと思います。
まずは多変量連関図を作成します。
# 必要なライブラリーのインポート
import seaborn as sns
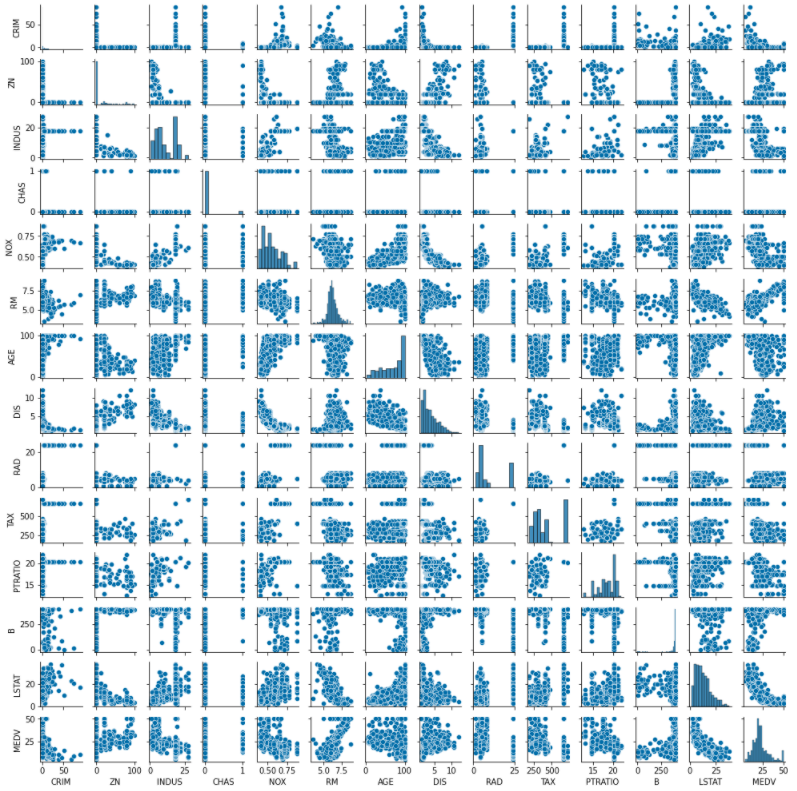
# 多変量連関図
sns.pairplot(df, size=1.0)
ぱっと見るとRM(1住戸あたりの平均部屋数)とMEDV(住宅価格)は正の相関がありそうですね。
二つに絞ってもう少し詳しく分析してみます。
# RM(1住戸あたりの平均部屋数)とMEDV(住宅価格)の関係
sns.regplot('RM','MEDV',data = df)
このように詳細に関係性を見るとRM(1住戸あたりの平均部屋数)とMEDV(住宅価格)は相関関係がありそうに見えます。
次に相関係数行列を求めてみたいと思います。
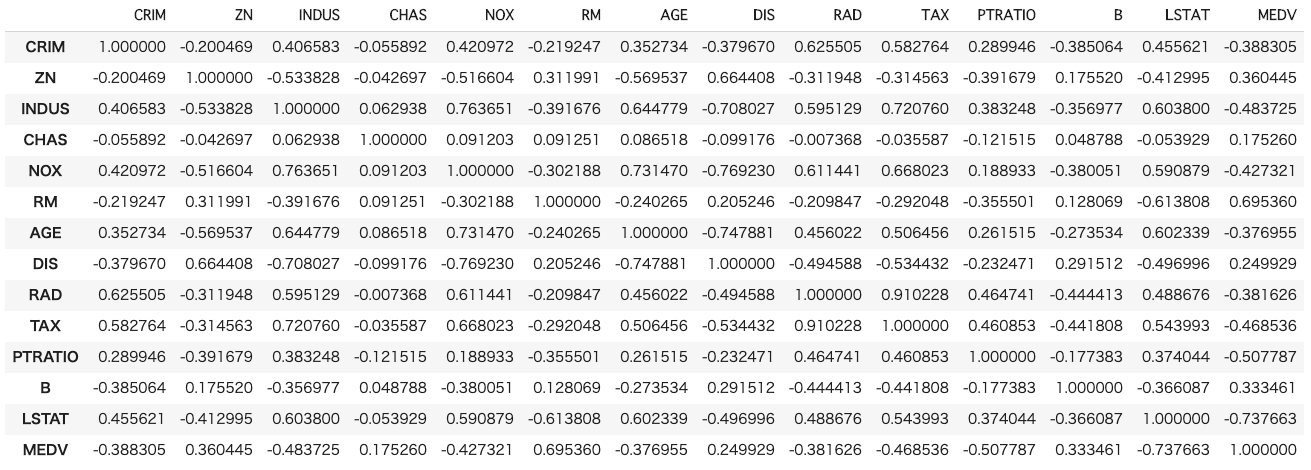
# 相関係数行列を算出
df.corr()
データの前処理
前処理ではデータに潜むゴミ(外れ値、異常値、欠損値)の除去を行う必要があります。
前処理はデータ分析において重要ですが、今回は欠損値有無だけ確認することとします。
# 欠損値の確認
df.isnull().sum()
CRIM 0
ZN 0
INDUS 0
CHAS 0
NOX 0
RM 0
AGE 0
DIS 0
RAD 0
TAX 0
PTRATIO 0
B 0
LSTAT 0
MEDV 0
dtype: int64
ボストン住宅の価格データは欠損値は無いため、このまま分析をすることにします。
データの正規化
今回は特徴量エンジニアリングは除きます(本当は実施するべきです)。
次は線形回帰モデルを構築するにあたってデータを学習データと評価データに分割します。
その後、説明変数のスケールを合わせるために正規化(標準化)を行います。
# ライブラリーのインポート
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# 学習データと評価データを作成
x_train, x_test, y_train, y_test = train_test_split(df.iloc[:, 0:13], df.iloc[:, 13],
test_size=0.2, random_state=1)
# データを標準化
sc = StandardScaler()
sc.fit(x_train) #学習用データで標準化
x_train_std = sc.transform(x_train)
x_test_std = sc.transform(x_test)
ここまで完了したら、手法の選択を行って回帰モデルを構築していきます。
今回は下記手法を実装することにしました。
- 線形回帰(重回帰)
- Ridge回帰
- Lasso回帰
- ElasticNet回帰
- RandomForest回帰
- GBDT(勾配ブースティング木)
- SVR(サポートベクターマシーン)
1. 線形回帰について
線形回帰の一般的な回帰式は下記のようになります。
\begin{eqnarray}
y = \sum_{i=1}^{n}(w_{i}x_{i})+b=w_{1}x_{1}+w_{2}x_{2}+・・・+w_{n}x_{n}+b
\end{eqnarray}
$w_i$ : 説明変数$x_i$に対する重み(回帰係数)
$b$ : バイアス(切片)
# ライブラリーのインポート
from sklearn.linear_model import LinearRegression
# スコア計算のためのライブラリ
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_error
# モデルの学習
lr = LinearRegression()
lr.fit(x_train_std, y_train)
# 回帰
pred_lr = lr.predict(x_test_std)
# 評価
# 決定係数(R2)
r2_lr = r2_score(y_test, pred_lr)
# 平均絶対誤差(MAE)
mae_lr = mean_absolute_error(y_test, pred_lr)
print("R2 : %.3f" % r2_lr)
print("MAE : %.3f" % mae_lr)
# 回帰係数
print("Coef = ", lr.coef_)
# 切片
print("Intercept =", lr.intercept_)
出力結果は下記です。
R2 : 0.779
MAE : 3.113
Coef = [-0.93451207 0.85487686 -0.10446819 0.81541757 -1.90731862 2.54650028
0.25941464 -2.92654009 2.80505451 -1.95699832 -2.15881929 1.09153332
-3.91941941]
Intercept = 22.44133663366339
評価指標の数字だけで判断するとまずいので、予測値と実測値を散布図で表してみようと思います。
# ライブラリーのインポート
import matplotlib.pyplot as plt
%matplotlib inline
plt.xlabel("pred_lr")
plt.ylabel("y_test")
plt.scatter(pred_lr, y_test)
plt.show()
この結果を見るとそこまで変な予測は行っていないと思います。
本当はここで精度向上に向けて詳細検討を行っていきますが、今回は別の手法を試してみます。
2. Ridge回帰について
Ridge回帰は線形回帰の損失関数に対して正則化項を付与したものになります。
線形回帰の損失関数は下記のようになります。
\begin{eqnarray}
L = (\boldsymbol{y} - X\boldsymbol{w})^{T}(\boldsymbol{y}-X\boldsymbol{w})
\end{eqnarray}
$\boldsymbol{y}$ : 目的変数の実測値をベクトル化したもの
$\boldsymbol{w}$ : 回帰係数をベクトル化したもの
$X$ : サンプル数$n$個、説明変数の数$m$個の実測値を行列化したもの
Ridge回帰では損失関数が下記のように変わります。
\begin{eqnarray}
L = (\boldsymbol{y} - X\boldsymbol{w})^{T}(\boldsymbol{y}-X\boldsymbol{w}) + λ||\boldsymbol{w}||_{2}^{2}
\end{eqnarray}
Ridge回帰では、上記のように重み$\boldsymbol{w}$のL2ノルムの2乗を加えることで正則化します。
pythonのコードは下記の通りです。scikit-learnを使用すると簡単です。
# ライブラリーのインポート
from sklearn.linear_model import Ridge
# モデルの学習
ridge = Ridge(alpha=10)
ridge.fit(x_train_std, y_train)
# 回帰
pred_ridge = ridge.predict(x_test_std)
# 評価
# 決定係数(R2)
r2_ridge = r2_score(y_test, pred_ridge)
# 平均絶対誤差(MAE)
mae_ridge = mean_absolute_error(y_test, pred_ridge)
print("R2 : %.3f" % r2_ridge)
print("MAE : %.3f" % mae_ridge)
# 回帰係数
print("Coef = ", ridge.coef_)
正則化パラメータは適当に設定しております(scikit-learnのデフォルトはalpha=1.0)
出力結果は下記です。
R2 : 0.780
MAE : 3.093
Coef = [-0.86329633 0.7285083 -0.27135102 0.85108307 -1.63780795 2.6270911
0.18222203 -2.64613645 2.17038535 -1.42056563 -2.05032997 1.07266175
-3.76668388]
予測値と実測値を散布図で表してみようと思います。
plt.xlabel("pred_ridge")
plt.ylabel("y_test")
plt.scatter(pred_ridge, y_test)
plt.show()
パラメータチューニングや変数選択を行っていないので、線形回帰とあまり変わらないですね。
3. Lasso回帰について
Lasso回帰とRidge回帰では、正則化項の部分が異なります。
Lasso回帰では損失関数が下記のように変わります。
\begin{eqnarray}
L = \frac{1}{2}(\boldsymbol{y} - X\boldsymbol{w})^{T}(\boldsymbol{y}-X\boldsymbol{w}) + λ||\boldsymbol{w}||_{1}
\end{eqnarray}
Lasso回帰では、正則化項がL1ノルムになっている部分がRidge回帰と異なります。
細かい部分は今回は省略します。
pythonのコードは下記の通りです。
# ライブラリーのインポート
from sklearn.linear_model import Lasso
# モデルの学習
lasso = Lasso(alpha=0.05)
lasso.fit(x_train_std, y_train)
# 回帰
pred_lasso = lasso.predict(x_test_std)
# 評価
# 決定係数(R2)
r2_lasso = r2_score(y_test, pred_lasso)
# 平均絶対誤差(MAE)
mae_lasso = mean_absolute_error(y_test, pred_lasso)
print("R2 : %.3f" % r2_lasso)
print("MAE : %.3f" % mae_lasso)
# 回帰係数
print("Coef = ", lasso.coef_)
正則化パラメータは適当に設定しております(scikit-learnのデフォルトはalpha=1.0)
出力結果は下記です。
R2 : 0.782
MAE : 3.071
Coef = [-0.80179157 0.66308749 -0.144492 0.81447322 -1.61462819 2.63721307
0.05772041 -2.64430158 2.11051544 -1.40028941 -2.06766744 1.04882786
-3.85778379]
予測値と実測値を散布図で表してみようと思います。
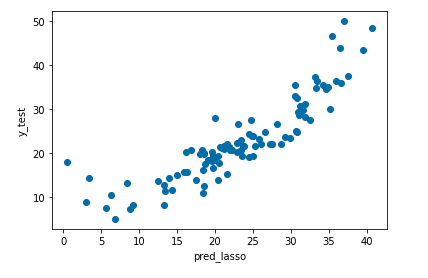
plt.xlabel("pred_lasso")
plt.ylabel("y_test")
plt.scatter(pred_lasso, y_test)
plt.show()
Lasso回帰もあまり変わらないですね。
4. ElasticNet回帰について
ElasticNet回帰とL1正則化とL2正則化を組み合わせた手法です。
pythonのコードは下記の通りです。
# ライブラリーのインポート
from sklearn.linear_model import ElasticNet
# モデルの学習
elasticnet = ElasticNet(alpha=0.05)
elasticnet.fit(x_train_std, y_train)
# 回帰
pred_elasticnet = elasticnet.predict(x_test_std)
# 評価
# 決定係数(R2)
r2_elasticnet = r2_score(y_test, pred_elasticnet)
# 平均絶対誤差(MAE)
mae_elasticnet = mean_absolute_error(y_test, pred_elasticnet)
print("R2 : %.3f" % r2_elasticnet)
print("MAE : %.3f" % mae_elasticnet)
# 回帰係数
print("Coef = ", elasticnet.coef_)
正則化パラメータは適当に設定しております(scikit-learnのデフォルトはalpha=1.0)
出力結果は下記です。
R2 : 0.781
MAE : 3.080
Coef = [-0.80547228 0.64625644 -0.27082019 0.84654972 -1.51126947 2.66279832
0.09096052 -2.51833347 1.89798734 -1.21656705 -2.01097151 1.05199894
-3.73854124]
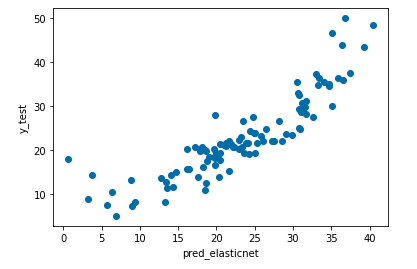
予測値と実測値を散布図で表してみようと思います。
plt.xlabel("pred_elasticnet")
plt.ylabel("y_test")
plt.scatter(pred_elasticnet, y_test)
plt.show()
ElasticNet回帰もあまり変わらなかったですね。
5. RandomForest回帰について
次は決定木系の回帰モデルを構築していきます。
まずは、RandomForest回帰です。
RandomForestとは、アンサンブル学習のバギングをベースに、異なる決定木をたくさん集めたものです。
決定木単体では過学習しやすいという欠点がありますが、RandomForestではこの問題に対応できる方法の1つです。
pythonのコードは下記の通りです。
# ライブラリーのインポート
from sklearn.ensemble import RandomForestRegressor
# モデルの学習
RF = RandomForestRegressor()
RF.fit(x_train_std, y_train)
# 回帰
pred_RF = RF.predict(x_test_std)
# 評価
# 決定係数(R2)
r2_RF = r2_score(y_test, pred_RF)
# 平均絶対誤差(MAE)
mae_RF = mean_absolute_error(y_test, pred_RF)
print("R2 : %.3f" % r2_RF)
print("MAE : %.3f" % mae_RF)
# 変数重要度
print("feature_importances = ", RF.feature_importances_)
パラメータはデフォルトのままです。
出力結果は下記です。
R2 : 0.899
MAE : 2.122
feature_importances = [0.04563176 0.00106449 0.00575792 0.00071877 0.01683655 0.31050293
0.01897821 0.07745557 0.00452725 0.01415068 0.0167309 0.01329619
0.47434878]
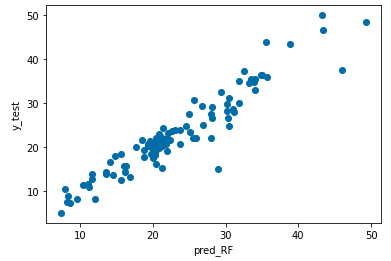
予測値と実測値を散布図で表してみようと思います。
plt.xlabel("pred_RF")
plt.ylabel("y_test")
plt.scatter(pred_RF, y_test)
plt.show()
回帰系のモデル(線形回帰、Ridge回帰、Lasso回帰、ElasticNet回帰)よりは良さそうですね。
RandomForestでも回帰はできるということを知っておくと便利だと思います。
また、RandomForestでは回帰係数は分からないため、変数重要度を見てモデルの妥当性とかを評価したりします。
6. GBDT(勾配ブースティング木)について
次はGBDT(勾配ブースティング木)です。
GBDTもアンサンブル学習の一つで、ある決定木の間違いを修正するような決定木を逐次的につくることで、汎化性能の向上を目指すアルゴリズムです。
pythonのコードは下記の通りです。
# ライブラリーのインポート
from sklearn.ensemble import GradientBoostingRegressor
# モデルの学習
GBDT = GradientBoostingRegressor()
GBDT.fit(x_train_std, y_train)
# 回帰
pred_GBDT = GBDT.predict(x_test_std)
# 評価
# 決定係数(R2)
r2_GBDT = r2_score(y_test, pred_GBDT)
# 平均絶対誤差(MAE)
mae_GBDT = mean_absolute_error(y_test, pred_GBDT)
print("R2 : %.3f" % r2_GBDT)
print("MAE : %.3f" % mae_GBDT)
# 変数重要度
print("feature_importances = ", GBDT.feature_importances_)
パラメータはデフォルトのままです。
出力結果は下記です。
R2 : 0.905
MAE : 2.097
feature_importances = [0.03411472 0.00042674 0.00241657 0.00070636 0.03040394 0.34353116
0.00627447 0.10042527 0.0014266 0.0165308 0.03114765 0.01129208
0.42130366]
予測値と実測値を散布図で表してみようと思います。
plt.xlabel("pred_GBDT")
plt.ylabel("y_test")
plt.scatter(pred_GBDT, y_test)
plt.show()
今までの手法の中で一番精度が良いですね。
ただ、GBDTはパラメータ設定をきちっとしないと過学習しやすいので気をつけてください。
7. SVR(サポートベクターマシーン)について
最後はSVR(サポートベクターマシーン)です。
サポートベクターマシーン(SVM)はもともと2値分類問題を解くために開発されたアルゴリズムです。そのため、分類問題しか使えないと思っている方もいるのではないでしょうか。
実は、SVMは回帰問題にも対応できるように、目的変数を連続値へ拡張したSVRがあります。SVRは非線形な回帰問題を比較的精度良く解ける特徴があります。
pythonのコードは下記の通りです。
# ライブラリーのインポート
from sklearn.svm import SVR
# モデルの学習
SVR = SVR(kernel='linear', C=1, epsilon=0.1, gamma='auto')
SVR.fit(x_train_std, y_train)
# 回帰
pred_SVR = SVR.predict(x_test_std)
# 評価
# 決定係数(R2)
r2_SVR = r2_score(y_test, pred_SVR)
# 平均絶対誤差(MAE)
mae_SVR = mean_absolute_error(y_test, pred_SVR)
print("R2 : %.3f" % r2_SVR)
print("MAE : %.3f" % mae_SVR)
# 回帰係数
print("Coef = ", SVR.coef_)
今回、カーネル関数は(linear:線形回帰)を使用しました。
他にも4種類のカーネル関数があるため、パラメータチューニングは必要です。
出力結果は下記です。
R2 : 0.780
MAE : 2.904
Coef = [[-1.18218512 0.62268229 0.09081358 0.4148341 -1.04510071 3.50961979
-0.40316769 -1.78305137 1.58605612 -1.78749695 -1.54742196 1.01255493
-2.35263548]]
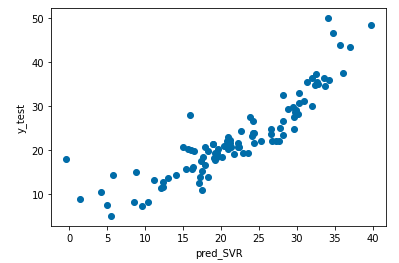
予測値と実測値を散布図で表してみようと思います。
plt.xlabel("pred_SVR")
plt.ylabel("y_test")
plt.scatter(pred_SVR, y_test)
plt.show()
SVRはRandomForestやGBDTと比べるとそこまで精度は良く無いですね。
スクリプトの纏め
今までのスクリプトを整理します。
# スコア計算のためのライブラリ
import pandas as pd
import numpy as np
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.svm import SVR
def preprocess_sc(df):
"""データを学習データと評価データに分割し、標準化を行う
Parameters
----------
df (pd.DataFrame) : データセット(説明変数+目的変数)
Returns
-------
x_train_std (pd.DataFrame) : 標準化後の学習データ(説明変数)
x_test_std (pd.DataFrame) : 標準化後の評価データ(説明変数)
y_train (pd.DataFrame) : 学習データ(目的変数)
y_test (pd.DataFrame) : 評価データ(目的変数)
"""
x_train, x_test, y_train, y_test = train_test_split(df.iloc[:, 0:13], df.iloc[:, 13],
test_size=0.2, random_state=1)
#データを標準化
sc = StandardScaler()
sc.fit(x_train) #学習用データで標準化
x_train_std = sc.transform(x_train)
x_test_std = sc.transform(x_test)
return x_train_std, x_test_std, y_train, y_test
def Linear_Regression(x_train_std, y_train, x_test_std):
"""線形回帰で予測する
Parameters
----------
x_train_std (pd.DataFrame) : 標準化後の学習データ(説明変数)
y_train (pd.DataFrame) : 学習データ(目的変数)
x_test_std (pd.DataFrame) : 標準化後の評価データ(説明変数)
Returns
-------
pred_lr (pd.DataFrame) : 線形回帰の予測結果
"""
lr = LinearRegression()
lr.fit(x_train_std, y_train)
pred_lr = lr.predict(x_test_std)
return pred_lr
def Ridge_Regression(x_train_std, y_train, x_test_std, ALPHA=10.0):
"""Ridge回帰で予測する
Parameters
----------
x_train_std (pd.DataFrame) : 標準化後の学習データ(説明変数)
y_train (pd.DataFrame) : 学習データ(目的変数)
x_test_std (pd.DataFrame) : 標準化後の評価データ(説明変数)
ALPHA (float) : 正則化パラメータα
Returns
-------
pred_ridge (pd.DataFrame) : Ridge回帰の予測結果
"""
ridge = Ridge(alpha=ALPHA)
ridge.fit(x_train_std, y_train)
pred_ridge = ridge.predict(x_test_std)
return pred_ridge
def Lasso_Regression(x_train_std, y_train, x_test_std, ALPHA=0.05):
"""Lasso回帰で予測する
Parameters
----------
x_train_std (pd.DataFrame) : 標準化後の学習データ(説明変数)
y_train (pd.DataFrame) : 学習データ(目的変数)
x_test_std (pd.DataFrame) : 標準化後の評価データ(説明変数)
ALPHA (float) : 正則化パラメータα
Returns
-------
pred_lasso (pd.DataFrame) : Lasso回帰の予測結果
"""
lasso = Lasso(alpha=ALPHA)
lasso.fit(x_train_std, y_train)
pred_lasso = lasso.predict(x_test_std)
return pred_lasso
def ElasticNet_Regression(x_train_std, y_train, x_test_std, ALPHA=0.05):
"""ElasticNet回帰で予測する
Parameters
----------
x_train_std (pd.DataFrame) : 標準化後の学習データ(説明変数)
y_train (pd.DataFrame) : 学習データ(目的変数)
x_test_std (pd.DataFrame) : 標準化後の評価データ(説明変数)
ALPHA (float) : 正則化パラメータα
Returns
-------
pred_elasticnet (pd.DataFrame) : ElasticNet回帰の予測結果
"""
elasticnet = ElasticNet(alpha=ALPHA)
elasticnet.fit(x_train_std, y_train)
pred_elasticnet = elasticnet.predict(x_test_std)
return pred_elasticnet
def RandomForest_Regressor(x_train_std, y_train, x_test_std):
"""RandomForest回帰で予測する
Parameters
----------
x_train_std (pd.DataFrame) : 標準化後の学習データ(説明変数)
y_train (pd.DataFrame) : 学習データ(目的変数)
x_test_std (pd.DataFrame) : 標準化後の評価データ(説明変数)
Returns
-------
pred_RF (pd.DataFrame) : RandomForest回帰の予測結果
"""
RF = RandomForestRegressor()
RF.fit(x_train_std, y_train)
pred_RF = RF.predict(x_test_std)
return pred_RF
def GradientBoosting_Regressor(x_train_std, y_train, x_test_std):
"""GBDTで予測する
Parameters
----------
x_train_std (pd.DataFrame) : 標準化後の学習データ(説明変数)
y_train (pd.DataFrame) : 学習データ(目的変数)
x_test_std (pd.DataFrame) : 標準化後の評価データ(説明変数)
Returns
-------
pred_GBDT (pd.DataFrame) : GBDTの予測結果
"""
GBDT = GradientBoostingRegressor()
GBDT.fit(x_train_std, y_train)
pred_GBDT = GBDT.predict(x_test_std)
return pred_GBDT
def SVR_Regression(x_train_std, y_train, x_test_std):
"""SVRで予測する
Parameters
----------
x_train_std (pd.DataFrame) : 標準化後の学習データ(説明変数)
y_train (pd.DataFrame) : 学習データ(目的変数)
x_test_std (pd.DataFrame) : 標準化後の評価データ(説明変数)
Returns
-------
pred_SVR (pd.DataFrame) : SVRの予測結果
"""
svr = SVR()
svr.fit(x_train_std, y_train)
pred_SVR = svr.predict(x_test_std)
return pred_SVR
def main():
# データセットの読込み
boston = load_boston()
# データフレームの作成
# 説明変数の格納
df = pd.DataFrame(boston.data, columns = boston.feature_names)
# 目的変数の追加
df['MEDV'] = boston.target
# データの前処理
x_train_std, x_test_std, y_train, y_test = preprocess_sc(df)
pred_lr = pd.DataFrame(Linear_Regression(x_train_std, y_train, x_test_std))
pred_ridge = pd.DataFrame(Ridge_Regression(x_train_std, y_train, x_test_std, ALPHA=10.0))
pred_lasso = pd.DataFrame(Lasso_Regression(x_train_std, y_train, x_test_std, ALPHA=0.05))
pred_elasticnet = pd.DataFrame(ElasticNet_Regression(x_train_std, y_train, x_test_std, ALPHA=0.05))
pred_RF = pd.DataFrame(RandomForest_Regressor(x_train_std, y_train, x_test_std))
pred_GBDT = pd.DataFrame(GradientBoosting_Regressor(x_train_std, y_train, x_test_std))
pred_SVR = pd.DataFrame(SVR_Regression(x_train_std, y_train, x_test_std))
pred_all = pd.concat([pred_lr, pred_ridge, pred_lasso, pred_elasticnet, pred_RF, pred_GBDT, pred_SVR], axis=1, sort=False)
pred_all.columns = ["pred_lr", "pred_ridge", "pred_lasso", "pred_elasticnet", "pred_RF", "pred_GBDT", "pred_SVR"]
return pred_all
if __name__ == "__main__":
pred_all = main()
さいごに
最後まで読んで頂き、ありがとうございました。
ただ、回帰モデルを構築すると言っても様々な手法があることが分かっていただけたかなと思います。
また、scikit-learnを活用できることで簡単にどれも実装できる事が分かっていただけたかと思います。
実務ではここから、各モデルの評価やパラメータチューニング、特徴量エンジニアリング等をさらに行って
精度向上をしていく必要があります。
訂正要望がありましたら、ご連絡頂けますと幸いです。