Outline
- イントロ
- 多目的最適化
- 多目的ベイズ最適化
- 既存手法
イントロ
今回は**「多目的ベイズ最適化」**というテーマについて記事を書いていきます。多目的最適化に関しては詳しく説明しますが、ベイズ最適化に関しては以前自分が書いたこの記事で詳しく触れているので踏み込んだ説明はしません。
本記事の目的
- 多目的ベイズ最適化のモチベーションや評価方法を知ってもらう
多目的最適化が実世界への応用先が多いということ、そして単一の最適化とは最適解の定義が異なるということを知って欲しいという思いがあります。
多目的最適化
ということでまずは多目的最適化に関して説明していきます。読んで字のごとく、最適化したい目的関数が複数存在します。これらの目的関数を$f_1,\ldots,f_L$と表記します。各目的関数ごとに最小化なのか最大化なのかは異なる設定もありうると思うのですが、説明を簡単にするために今回はすべての目的関数で最小化を目的とします。つまり、すべての目的関数を同時に最小化する大域的最適解$x^{*}$を獲得するのが理想となります。
$$x^{*} = \arg\min_{x\in \mathcal{X}}f_{1},\ldots,f_{L}$$
しかし、多目的最適化のゴールは$x^{*}$を獲得することではありません。そもそも$x^{*}$が必ず存在するわけではありません。では多目的最適化のゴールは何かと言うと...
パレート最適解を全て獲得すること
です。というわけでパレート最適解に関して説明していきます。
パレート最適解
現実世界の多目的最適化問題では、目的関数間にトレードオフの関係があることが多いです。
料理の総合的な評価を例にしてみましょう。料理に対する評価というのは複数の項目によってなされます。一例ですが、
- 味
- 見た目
- 香り
- 値段 (外食の場合)
といった項目を同時に最適化しようと思った時に、理想は1~4全部最適な料理を作ることです。しかし世の中そんなに甘くありません。例えば味や見た目にこだわろうと食材に上等なものをふんだんに使ってしまうとその分値段をあげないといけなくなります。香りにこだわりすぎると見た目や味が悪くなってしまうかもしれません。といった風にどれかをよくしようとすると他の目的関数が悪くなってしまうことがありうるわけです。なので理想解$x^{*}$の代わりにパレート最適解というのを定義します。その準備段階として支配関係というものを定義します。
支配関係
支配関係は目的関数空間上の任意の2点間で定義される関係です。ここからは入力空間上のある2点$x_{i}$, $x_{j}$に対応する目的関数 $f(x_i) = [f_{1}(x_{i}), f_2(x_i)]^{\top}$, $f(x_j) = [f_{1}(x_{j}), f_2(x_j)]^{\top}$
平たくいうと**$x_{j}$が全ての目的関数で$x_i$に負けてるとき、$x_i$は$x_j$を支配している**と言います。下の図がそれを示したもので、最小化の文脈で$x_i$の方が$f_1$, $f_2$どちらの値も$x_j$より小さいです。
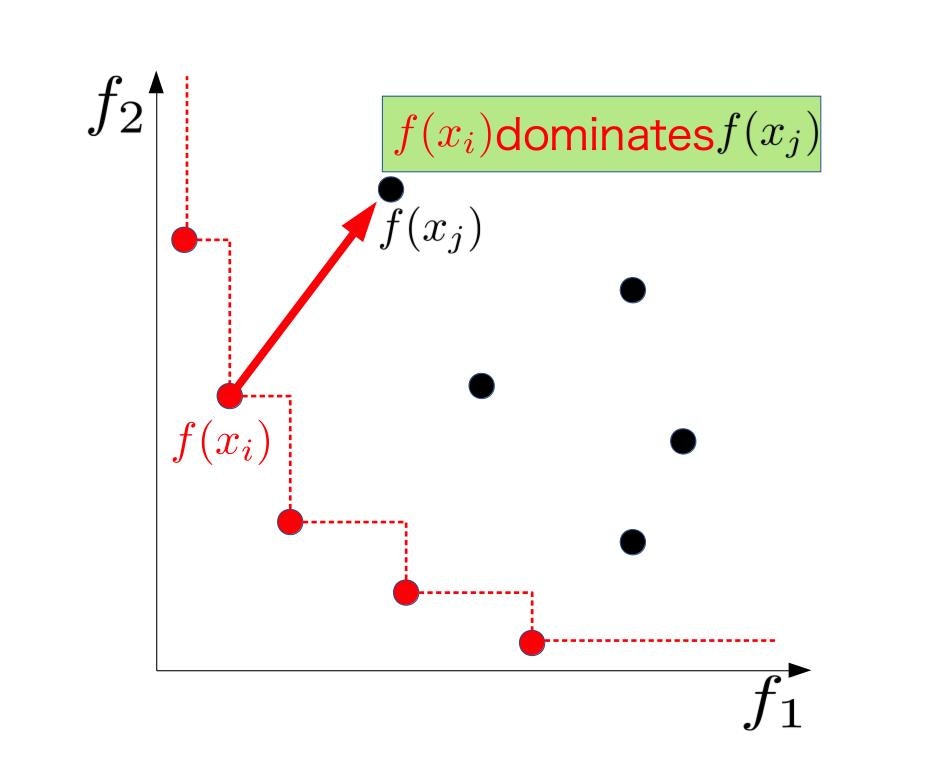
この支配関係を$x_i \succeq x_j$と表記することにします。数式できちんと定義すると、
$$x_i \succeq x_j \Leftrightarrow f_l(x_i) \le f_l(x_j), \forall l \in 1,\ldots,L,$$と定義できます。
パレート最適
いよいよパレート最適の説明をしていきます。ある点$x_i$が他のどの点にも支配されていないとき、$x_i$はパレート最適であると定義されます。先ほどの図中の赤い点は全てパレート最適の定義を満たしています。一般にパレート最適解は複数存在し、その集合をパレートセット$\mathcal{X}^{*}$, 対応する目的関数値の集合をパレートフロンティア$\mathcal{F}^{*}$とします。$\mathcal{X}^{*}$の定義は以下の通りです。
$$\mathcal{X}^{*} = \{x \in \mathcal{X}\mid \forall x^{\prime} \in \mathcal{X} \backslash \{x\}, x^{\prime}\not\succeq x \}$$
というわけで、多目的最適化のゴールは、
パレートセットの要素を全て獲得することです。
ゴールがはっきりしたところで、では最適化がどれだけ達成されているかをどう評価するかを説明していきます。多目的最適化では様々な評価指標があるのですが、今回はパレート超体積という指標を紹介します。
まず、現在観測ずみのデータ集合内で定義されるパレートフロンティアをCurrent Pareto Frontier、空間全体で定義される真のパレートフロンティアをTrue Pareto Frontierと呼ぶことにします。下に示した図の青い点がCurrent Pareto Frontier、黒い点がすでに他の点に支配されているパレート最適ではない点です。このとき図の赤い点のような基準点を設けることで複数の超直方体を組み合わせたような図形ができます。この図形の超体積をパレート超体積と呼びます。このパレート超体積は単調増加でTrue Pareto Frontierを全て獲得した際に最大となります。
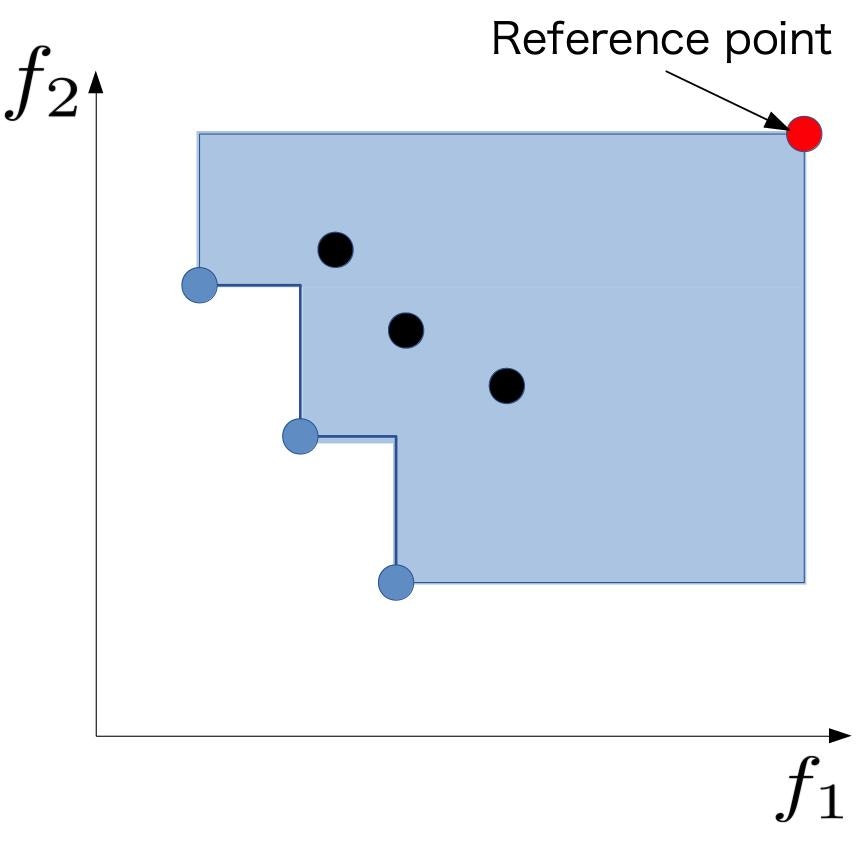
多目的ベイズ最適化
多目的ベイズ最適化は読んで字のごとし、多目的最適化をベイズ最適化の枠組みで解きます。ベイズ最適化が用いられる際の問題設定をおさらいしておきましょう。
- 最適化したい目的関数がブラックボックス
- 一回の観測に膨大なコストがかかる
これらの設定から、獲得関数という指標に基づいてより少ない観測回数で最適化を達成することがベイズ最適化の目的でした。
つまりさきほどの多目的最適化のゴールから、多目的ベイズ最適化は
すべてのパレート最適解を少ない観測回数で獲得すること
が目的であると言えます。ここで最適化対象である目的関数にいくつかの仮定を置いておきます。
- L個の目的関数はそれぞれ独立なガウス過程に従う
- 観測の際に乗るノイズはすべての目的関数で共通の大きさ
- ある入力で実験を行うとすべての目的関数の値が同時に得られる
というわけでここから多目的ベイズ最適化の獲得関数を3つほど紹介していきます。
既存手法
ParEGO
元論文 : ParEGO: a hybrid algorithm with on-line landscape approximation for expensive multiobjective optimization problems
ParEGOはベイズ最適化の手法の中で最も古典的な手法です。
ParEGOのコンセプトはズバリ線形化。多目的最適化問題を単一目的関数の最適化問題に落とし込みます。具体的にどう線形化するのか説明するために一つ新たな定義をば...
すでに観測ずみの入力点がN個、$x_1,\ldots,x_N$とそれに対応する目的関数値のベクトルを$f(x_1),\ldots,f(x_N)$とします。ここで各$x$に関して以下のような重み付き線形和を考えます。
$$f_\theta(x_{i}) = \max_{l\in1,\ldots,L} \theta_l f_l(x_i) + \rho\sum_{l=1}^{L}\theta_l f_l (x_i) $$
ただし、$\theta_l$は一様分布からサンプリングされる重みで、$\rho$はハイパーパラメータです。元論文では0.05に設定されていました。この線形化によって得られる$f_{\theta}$に関してベイズ最適化を適用します。ParEGOのメリットの一つは計算コストの軽さです。線形化することによりガウス過程回帰の事後分布の計算を目的関数の個数分する必要がありません。獲得関数自体も単一のベイズ最適化なので後述の手法に比べると軽いです。その一方で本来の最適化対象を最適化しているわけではないのでパレート解の網羅的探索という観点からは良い性能を示さないこともあります。
Expected Hypervolume Improvement (EHI)
元論文 : The computation of the expected improvement in dominated hypervolume of Pareto front approximations
EHIは単一のベイズ最適化のポピュラーな獲得関数であるEIのアイデアを多目的最適化に応用させたものです。EHIのアイデアは、パレート超体積の増加量の期待値が最大の点を獲得することです。
EHIは獲得関数自体は解析的な形で書けるのですが、目的関数の数が増えるにつれてその計算コストが指数的に増加していきます。そのため目的関数が4個以上の設定でEHIの実験を行なっている論文はあまりありません。しかし、EHIの計算の高速化を図る研究もなされているようです。
S-metric Selection Efficient Grobal Optimization (SMSego)
元論文 : Multiobjective Optimization on a Limited Budget of Evaluations Using Model-Assisted S-Metric Selection
最後にSMSegoを紹介します。これもEHIと同様超体積を軸に獲得関数を設計します。ある入力$x$に関してガウス過程回帰によって計算される事後平均と分散をそれぞれ$\mu(x)$, $\sigma^{2}(x)$とすると、
$$\mu(x) - \alpha \sigma(x)$$という下側信頼区間を考えます。現在の観測ずみデータ集合にこの下側信頼区間を加えた時に、最もパレート超体積を増加させる点を次に観測します。これは各点が超体積をどれだけ増加させるかを楽観的に見積もっていることになります。$\alpha$はハイパーパラメータです。SMSegoはEHI同様目的関数の数が増えると計算コストが重くなります。そもそもパレート超体積の計算自体が重いため、超体積を指標とするとどうしても計算コストと戦う宿命にあるのでしょう。ただパレート超体積の効率的な計算法は、それだけでも一つの論文にできるような結構重要なトピックでもあります。
終わりに
というわけで多目的ベイズ最適化に関してつらつらと説明してきましたが、もし質問やご指摘などありましたらコメントいただけると嬉しいです。
また、今回紹介した3つの手法に関してはpythonでの実装をGithubにてまとめてあるのでもしよかったら遊んでみてください。
Github