ベイズ最適化に関するまとめ

はじめに

この記事は, ベイズ最適化という言葉を聞いたことがあるけど中身をよく知らない, 実際に使ってみたいけどどんな手法があるか分からない, といった方をターゲットにしています.
記事の流れとしては,
1. はじめに
2. 問題設定
3. ガウス過程回帰
4. ベイズ最適化の手法紹介
5. まとめ

問題設定

まずはベイズ最適化が考えている問題設定と達成したいゴールに関してここで整理しておきます.

ブラックボックス関数の最適化

ベイズ最適化は, ブラックボックス関数の最適化に適用されます.
最適化というのは目的関数 $f(x)$の最適解$x^{*}$を手に入れることが目的です.
最適解を求める方法はいくつかありますが, $f(x)$の微分を利用するのがわかりやすいと思います. (数理最適化に関してはあまり詳しくないのでこれ以上の言及はやめておきます)
その一方でブラックボックス関数というのは微分ができません. つまり関数の形状が分からないのです. 具体例をあげると, 化学とか材料分野の実験結果 (結晶格子を色々変えた時の燃料電池のエネルギーなど...)はブラックボックスですね. 最近ホットな話題だとニューラルネットをはじめとする, ハイパーパラメータチューニングが必要な機械学習手法の予測精度もそうです.
後者の話題に関してはPFNがOptunaというツールを出しています. (公式が詳しいドキュメントを公開しているのでこちらを読んでみてください)
こういったブラックボックス関数の最適化が通常どういう風に行われるかというのをニューラルネットのハイパーパラメータチューニングを例に説明していきます.

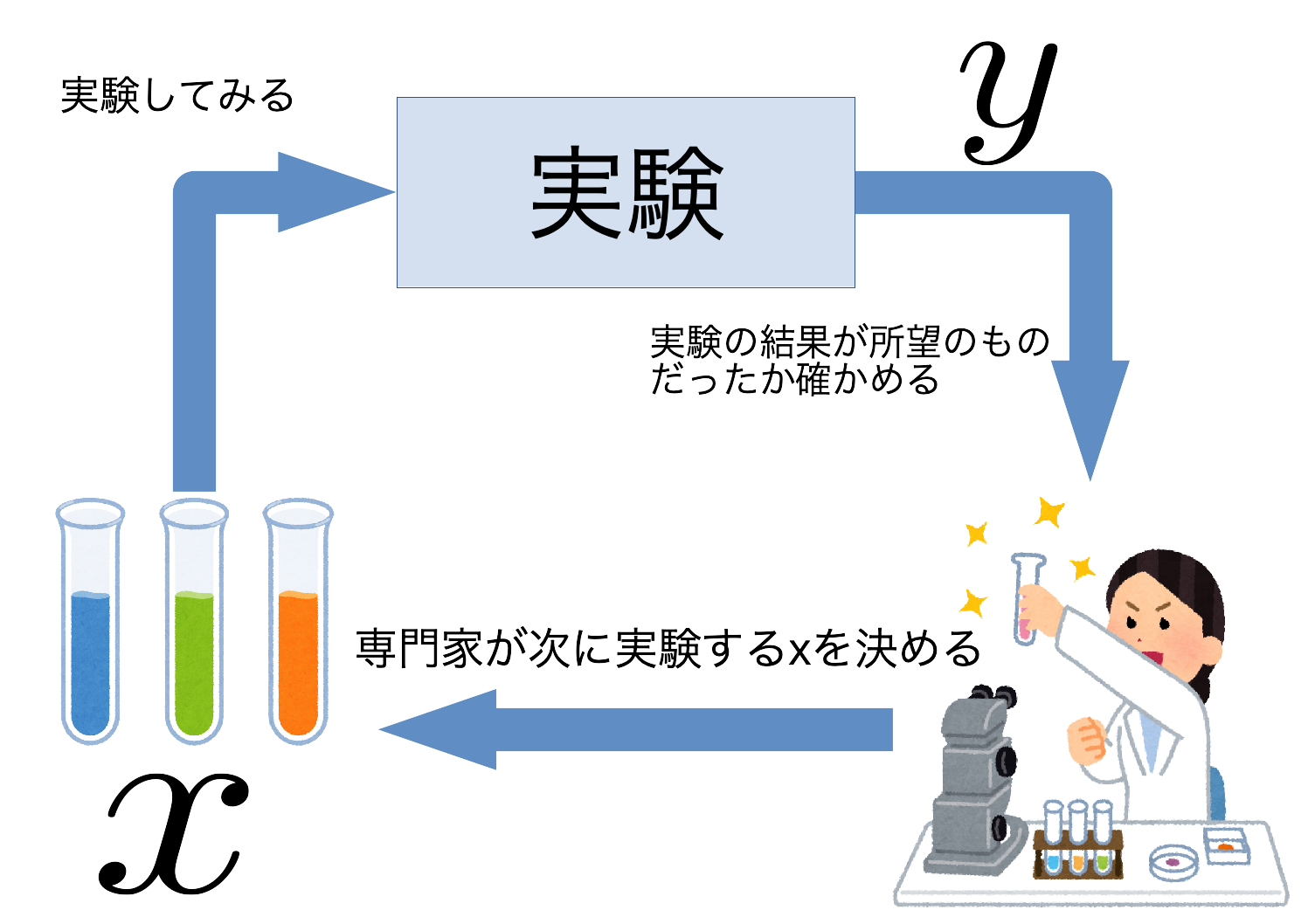
ハイパーパラメータを$x \in \mathbb{R}^{d}$, その$x$で実験した際の予測精度を$f(x) \in \mathbb{R}$とします. 予測精度は実際に学習と予測をやってみないと分からないため目星をつけた$x$に対して一度実験を回す必要があります. その結果得られた$f(x)$が所望の値でなかったとき, 次に実験する$x$を決めてまた実験を回す...というサイクルを, $x^{*}$が得られるまで繰り返します. 次に実験する$x$の決め方に関しては, パラメータの範囲をグリッドに切って網羅的に組み合わせを試したり, 専門家の知見を元に決めたりします. しかし, 化学実験やニューラルネットの学習と予測にはコスト(お金や時間)がかかる場合が多いです. そのため網羅的にやるのは現実的ではなく, 出来るだけ実験回数を減らして所望の$x^{*}$を手に入れたいわけです.
これがベイズ最適化の目的となります.
まとめると,
1. ベイズ最適化ではブラックボックス関数の最適化を目的とする.
2. $f(x)$の観測回数はなるべく少なくしたい.

獲得関数

ベイズ最適化の問題設定と目的に関して説明しましたが,
じゃあどうやって観測回数を減らすの？
という話を次にしていきます.
結論から言うと, 最適化に有益そうな点を優先的に観測します.
最適化に有益そうってどんな点やねんというのは後々説明しますが, 今までは専門家が有益そう, もしくは最適解っぽいと思う$x$を観測したわけですが, ベイズ最適化では獲得関数と呼ばれる指標を導入し, 獲得関数を最大化する$x$を次に観測します. この獲得関数をどう設計するかというのがベイズ最適化の肝になっています.

ガウス過程回帰

ベイズ最適化では, 目的関数$f(x)$の回帰モデルを構築し, そのモデルによる予測を基に獲得関数を計算します. 今回はベイズ最適化でよく用いられるガウス過程回帰に関して説明していきます.
ただカーネル関数の話や事後分布の導出に関しては割愛します.
まず, 入力$x$と対応する観測値$y \in \mathbb{R}$の間に次のような関係を仮定します.
$$y = f(x) + \varepsilon$$
$\varepsilon$というのは観測ノイズで, 平均0, 分散$\sigma^{2}_{\rm noise}$の正規分布から発生します. 普通の線形回帰では, $x$に対して$f(x)$の予測値を推定するようなモデルを構築します. その一方でガウス過程回帰では, $f(x)$がガウス分布に従うと仮定しデータから$f(x)$を確率分布の形で推定します. データ集合$\mathcal{D}$が得られたときの$f(x)$は次のような正規分布に従います.
$$f(x) | x, \mathcal{D} \sim \mathcal{N}(\mu (x), \sigma^{2}(x))$$
このとき, $\mu(x)$, $\sigma^{2}(x)$をそれぞれ予測平均, 予測分散と呼びます.
ガウス過程回帰のメリットとして, 回帰の不確かさを評価することができることが挙げられます.

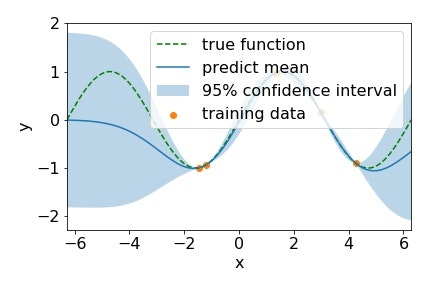
上の具体例でそのメリットに関して説明していきます.
このグラフは緑点線の真の関数を, オレンジの訓練データから予測したものです. 青実線が平均, 薄青の領域が95%信頼区間となっていて, 平均と信頼区間の幅が不確かさの度合いを表しています. すでに獲得できている点やその近傍では不確かさが残っておらず, 平均も真の関数の形状を捉えられています. その一方で全く点が獲得できていない範囲では, 不確かさが大きく残っており平均も真の関数から離れています. このように目的関数を確率的なモデルで回帰することで得られる不確かさの情報をベイズ最適化では獲得関数の中でフル活用しています.
ガウス過程回帰, およびガウス過程に関してはガウス過程と機械学習という本が非常にわかりやすく参考になると思うので, ぜひ読んでみてください.

ベイズ最適化の手法紹介

というわけでここからが本題. ベイズ最適化の手法に関して紹介をしていくのですが, その前にベイズ最適化における重要な考え方"探索と活用"という考え方を導入しておきます.

探索と活用とは

まずそれぞれの意味合いから説明します.

• 探索

  • まだデータが全然獲得できていない部分 (不確かさが大きく残っている)の点を獲得すること

• 活用

  • 現状得られているデータで最適解っぽい点の近くの点を獲得すること

この二つの方針のどちらを重視すべきかというのは, 最適化の進み具合によって変わってきます.

最適化の序盤, すなわちまだ獲得データ数が少ないとき

データ数が少ないということはまだ最適解がいそうな範囲の目星もついていないわけです. この段階で今持ってるデータから最適解っぽいとこを取ってきても, 見当違いな可能性の方が高そうです. むしろまだ全然情報が集まってない範囲から点を取ってきて, 早いところ最適解がいそうな範囲の目星をつけたいですよね? なので活用よりかは探索に重きをおきたくなります.

最適化の終盤, そこそこデータが集まってきたとき

ある程度のデータが集まり, 予測平均から最適解の目星をつけれそうになってきたら, いよいよそれを参考に最適解を当てにいきたいと思うわけです. つまり探索より活用に重きをおきます.

一言でまとめると,
初めは探索して最適解の目星がついたら当てにいく

探索と活用というのはトレードオフの関係にあるため, 片方を重視するともう片方がおろそかになってしまいます. ここからベイズ最適化の有名な獲得関数に関して紹介していきますが, 今回はこの探索と活用の観点を重視していきたいと思います. また, 獲得関数の計算の詳細は元論文を参照してください.
以降獲得関数を$\alpha(x)$, 次に観測する点を$x_{\rm next}$と表記し, $f(x)$の最大化問題を考えることにします.

Probability of Improvement (PI)

参考文献

まずはもっとも古典的な獲得関数であるPIから, PIは現状獲得できている中での最大値$y_{\rm max}$よりも大きくなる確率が最大の点を選択します. 式で書くと,
$$x_{\rm next} = \arg max_{x } P(f(x) \ge y_{\rm max}), $$
となります. これは$f(x)$の予測平均と予測分散を用いて簡単に計算することができます.
PIはかなり活用に寄った手法で局所解にハマりやすい性質があります.

Expected Improvement (EI)

参考文献

EIは$y_{\rm max}$からどれだけ改善するかの期待値を獲得関数とします.

$$x_{\rm next} = \arg max_{x } \mathbb{E}[\max(f(x) - y_{\rm max}, 0)], $$

$f(x) - y_{\rm max}$というのが現状持ってる最大値からの改善量です. この値が負になると, 改善する見込みがないということなので$0$にしています. PIが$y_{\rm max}$を改善するかどうかしか見ていないのに対して, EIは$y_{\rm max}$からどれだけ改善するかを指標としているので, PIよりかは局所解にハマりにくいです. それでも活用に重きを置いているというのが自分の印象ですが...

Gaussian Process Upper Confidence Bound (GP-UCB)

参考文献
続いてGP-UCBですが, これは探索と活用のトレードオフをハイパーパラメータによって制御しています. 式で書くとこんな感じ.
$$x_{\rm next} = \arg max_{x} \mu(x) + \beta^{1/2}_{t}\sigma(x). $$

$\beta_{t}$というのがパラメータになっていて, 添字の$t$はイテレーション数を示しています.

$\beta_{t}$が小さいとき

獲得関数としては予測平均$\mu(x)$が支配的になるため, 活用に重きが置かれます.

$\beta_{t}$が大きいとき

先ほどとは別に予測偏差$\sigma(x)$が支配的になるため, 探索に重きが置かれます.

このことから, ハイパーパラメータ$\beta_{t}$が探索と活用のトレードオフを制御していることがわかります. この$\beta_{t}$ですが, イテレーションに対してlogスケールで増加していくように設定することが多いそうです.
GP-UCBのアドバンテージとして, 理論解析が論文中で多くなされていることが挙げられます. (これも詳細は割愛)

Predictive Entropy Search (PES)

参考文献
PESは, 最適解$x^{*}$と獲得関数を計算しようとしている$x$の目的関数値$f(x)$の相互情報量を獲得関数とします.
$$x_{\rm next} = \arg max_{x} I({x, f(x)}; x^{*}|\mathcal{D})$$
この相互情報量というのは条件付きエントロピーの形で以下のように分解することができます.

\begin{align}
I({x, f(x)}; x^{*}|\mathcal{D}) &= H(f(x) | x, \mathcal{D})  \\ 
&- \mathbb{E}_{x^{*}}[H(f(x)|x, \mathcal{D}, x^{*})]
\end{align}

今, $f(x)$というのは正規分布に従う確率変数なのでそのエントロピーというのは容易に計算できます. ところが第二項の$x^{*}$によって条件づけられると扱いが難しくなります. PESではこの第二項の計算を, Random Feature mapやExpectation Propagationといった手法を利用して近似計算しています. GP-UCBのような理論解析はないのですが, 実践的にはPESが他の手法よりも優れたパフォーマンスを出すことが知られています.

Max-value Entropy Search (MES)

参考文献
最後にMESを紹介します. MESは 最適値$f^{*}$と獲得関数を計算しようとしている$x$の目的関数値$f(x)$の相互情報量を獲得関数とします.
$$x_{\rm next} = \arg max_{x} I({x, f(x)}; f^{*}|\mathcal{D})$$
PESが入力空間での最適解を考えていたのに対して, MESは出力空間に目を向けています. この式もPESのとき同様, 条件付きエントロピーに分解することができます.

\begin{align}
I({x, f(x)}; f^{*}|\mathcal{D}) &= H(f(x) | x, \mathcal{D})  \\ 
&- \mathbb{E}_{f^{*}}[H(f(x)|x, \mathcal{D}, f^{*})]
\end{align}

やはり第二項の計算を工夫する必要があるのですが, MESはPESに比べるとリーズナブルな近似をしており, 直感的にも分かりやすい計算方法になっています. (要望があれば詳細を書きます)
PESとMES両方に言えることなのですが, 最適解(or 最適値)との相互情報量というのは空間全体を考慮できている大域的な指標になっています. さらに, GP-UCBのようなハイパーパラメータが存在しないにも関わらず, 探索と活用のトレードオフを考慮できていることが強みとなっています.

まとめ

という訳で今回はベイズ最適化の代表的な手法を簡単に紹介しました. どの手法に関してもお気持ち程度にしか触れていないので詳しいことは元論文を読むと分かると思います. 質問などありましたらコメントお願いします.