はじめに
実務でベイズ推論をやる必要があるので、事前知識として「ベイズ推論による機械学習入門」を読んで実装しています。
https://www.amazon.co.jp/dp/4061538322/ref=cm_sw_r_tw_dp_U_x_mxt0CbTB5QCRP
この本の5.3隠れマルコフモデルの実装を、自分の備忘録を兼ねてやってみます。今回は、隠れマルコフモデルによりサンプルを生成してプロットしてみるところをやります。次回以降で、そのデータを(パラメータは知らないものとして)推論してみることにします。余裕があれば、何か実データ(株価など?)もやってみることにします。
モデルの詳細の説明は本と被ってしまうので、興味のある方は本を読んでみてください。この記事は実装中心です。
隠れマルコフモデル概要
確率モデルの1つで、時系列の相関を含むモデルです。音声認識、バイオインフォマティクス、形態素解析(自然言語処理)、楽譜追跡、部分放電など、時系列パターンの認識に応用されている(wikipediaより)とのことです。株価などにも応用できそうですね。

隠れマルコフモデル
時系列で状態 $s$ (潜在変数)が変化し、その状態 $s$に基づいて $x$ が生成されます。潜在変数sは、初期値のみカテゴリ分布に従って生成されます。
$$
p(s_1|\pi) = Cat(s_1|\pi)
$$
$\pi$ には事前分布としてディリクレ分布を導入
$$
p(\pi) = Dir(\pi|\alpha)
$$
時系列の次のデータからは、直前の潜在変数 $s_{n-1}$ の値により潜在変数 $s_{n}$ が生成されます。
$$
p(\boldsymbol{S}|\pi, \boldsymbol{A}) = p(s_1|\pi)\prod_{n=2}^N{p(s_n|s_{n-1, \boldsymbol{A}})}
$$
$\boldsymbol{A}$はK×Kのサイズの状態遷移確率。
$x$はこのカテゴリsに基づいて生成されるが、生成モデルはポアソン分布でもガウス分布でも選べます。例えばポアソン分布を仮定すると、
$$
p(x_n|s_n, \lambda) = \prod_{k=1}^N{Poi(x_n|\lambda_k)^{s_{n,k}}}
$$
また、パラメータ $\lambda_k$ の事前分布として、ガンマ分布を導入することにします。
$$
p(\lambda_k)=Gam(\lambda_k|a,b)
$$
事前準備
このモデルに従って、サンプルを生成してプロットしてみることにします。隠れマルコフモデルは混合モデルなので、事前準備として、必要な基本の確率モデルを実装してみます。
ディリクレ分布
カテゴリ分布のパラメータπの事前分布であるディリクレ分布を実装します。ディリクレ分布は以下のような分布です。
$$
Dir(\pi|\alpha) = C_D(\alpha)\prod_{k=1}^{K}\pi_k^{\alpha_k-1}
$$
ただし
$$
C_D(\alpha)=\frac{\Gamma(\sum_{k=1}^{K}\alpha_k)}{\prod_{k=1}^{K}\Gamma(\alpha_k)}
$$
αの値に応じて、πの確率をプロットするコードを書いてみます。今回は、カテゴリ数は3にしてみました。
def plot_dir_ln(alpha):
pi0 = np.arange(0,1, 0.05)
pi1 = np.arange(0,1, 0.05)
#指数や階乗が出てきて途中でオーバーフローしやすいので、対数をとって計算します。
lncd_c=1
for i in range(1, np.sum(alpha)): lncd_c+=math.log(i)
lncd_p = 1
for i in range(len(alpha)):
for j in range(1, alpha[i]):
lncd_p+=math.log(j)
lncd = lncd_c-lncd_p
p=np.zeros((len(pi0),len(pi1)))
x=np.zeros((len(pi0)*len(pi1)))
y=np.zeros((len(pi0)*len(pi1)))
z=np.zeros((len(pi0)*len(pi1)))
k=0
for i in range(len(pi0)):
for j in range(len(pi1)):
if pi0[i]>0 and pi1[j] and 1-pi0[i]-pi1[j] >0:
lnp = lncd + (alpha[0]-1)*math.log(pi0[i]) + (alpha[1]-1)*math.log(pi1[j]) + (alpha[2]-1)*math.log(1-pi0[i]-pi1[j])
p[i][j]=math.exp(lnp)
x[k]=pi0[i]
y[k]=pi1[j]
k+=1
k=0
for j in range(len(p)):
for i in range(len(p)):
z[k]=p[i][j]
k+=1
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.bar3d(x, y, 0, 0.04, 0.04, z)
plot_dir_ln([10,10,10])
plot_dir_ln([10,30,20])
以下のように出力されました!
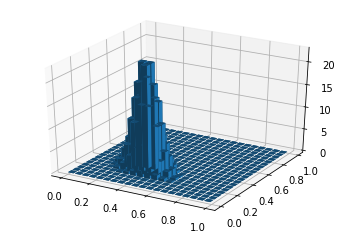
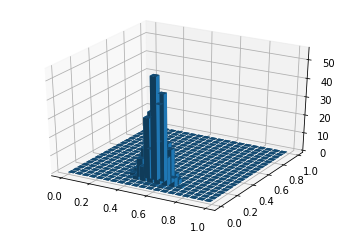
例えば、パラメータα=[10,10,10]のときは、確率が最大となるπはπ=[0.33, 0.33, 0.33]位、α=[10,30,20]のときは、π=[0.15, 0.5, 0.35]位になるようです。ちなみにπ=[0.33, 0.33, 0.33]のカテゴリ分布というのは、3つのカテゴリが同じ確率で出現するということです。
ガンマ分布
次はポアソン分布のパラメータλの事前分布であるガンマ分布を実装します。ガンマ分布は以下のような分布です。
$$
Gam(\lambda|a,b) = C_G(a,b)\lambda^{a-1}e^{-b\lambda}
$$
ただし
$$
C_G(a,b)=\frac{b^a}{\Gamma(a)}
$$
パラメータa, bの値に応じて、λの確率をプロットするコードを書いてみます。
def plot_gam(a, b):
lam = np.arange(1,100, 0.1)
#こちらもオーバーフローしやすいので対数をとって計算
lna = 0
#本当はガンマ関数ですが、aを整数に限ることにして階乗で計算
for i in range(1, a): lna+=math.log(i)
lncg = a*math.log(b)-lna
p = []
for item in lam:
lnp = lncg+(a-1)*math.log(item)-b*item
p.append(math.exp(lnp))
plt.plot(lam,p)
plt.show
plot_gam(1200,20)
plot_gam(450,15)
plot_gam(20, 4)
このようにプロットされました!
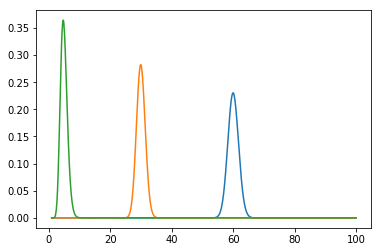
[a,b] = [1200,20]のが青、[450,15]のがオレンジ、[20, 4]のが緑です。ガンマ分布の期待値はa/bになるので、合っていそうです。
サンプルデータの生成
これらの事前分布を使って、サンプルを生成してみます。
カテゴリ分布のパラメータπの生成
まずは、最初のサンプルのカテゴリをカテゴリ分布により生成するため、カテゴリ分布のパラメータπを、事前分布であるディリクレ分布により生成します。本当は、確率なので、ディリクレ分布に従って確率的に生成しますが、今回はそこは端折って、確率が最大に近いπに決めてしまうことにします。
alpha = [50,30,10] #事前分布のパラメータはとりあえず決め打ちする
lncd_c=1
for i in range(1, np.sum(alpha)): lncd_c+=math.log(i)
lncd_p = 1
for i in range(len(alpha)):
for j in range(1, alpha[i]):
lncd_p+=math.log(j)
lncd = lncd_c-lncd_p
p_max = 0
for i in range(1, 100):
ii = i/100
for j in range(1, 100):
jj = j/100
if 1-ii-jj >0:
lnp = lncd + (alpha[0]-1)*math.log(ii) + (alpha[1]-1)*math.log(jj) + (alpha[2]-1)*math.log(1-ii-jj)
p=math.exp(lnp)
if p>p_max:
p_max=p
pi0 = ii
pi1 = jj
pi = [pi0, pi1, 1-pi0-pi1]
print("pi:", pi)
あまりコードがきれいじゃなくてすみません。上記のコードを実行すると、πの値は
π = [0.57, 0.33, 0.10]
のように生成されました。カテゴリが3つなので、1つ目のカテゴリになる確率が57%位、2番目が33%位、3番目が10%位ということになります。
最初のカテゴリの生成
先ほど生成したπにより最初のカテゴリを生成します。ここはちゃんと確率的に、乱数を使ってカテゴリを生成しました。
s=[]
r = random.random()
if r<=pi[0]: s.append(0)
elif r<=pi[0]+pi[1]: s.append(1)
else: s.append(2)
print("最初のカテゴリ:", s[0])
もちろん、確率的にカテゴリ0, 1, 2の中から選ばれますが、今回の私の実行では一番確率の高い「0」が生成されました。
2番目以降のカテゴリの生成
2番目以降のカテゴリは、状態遷移確率Aによって生成されます。このコードを書いて2番目から100番目のカテゴリを生成してみます。
※追記:後から分かったのですが、本の推論の方では、AもK次元のディリクレ分布から生成していました。とりあえずサンプルデータ生成はこのままで進めます。
※追記2:後、本ではAの行列が逆ですね。
A=[[0.95, 0.045, 0.005],[0.025, 0.95, 0.025],[0.005, 0.045, 0.95]]
for i in range(1, 100):
r = random.random()
if r<A[s[i-1]][0]: s.append(0)
elif r<A[s[i-1]][0]+A[s[i-1]][1]: s.append(1)
else: s.append(2)
t = range(0, len(s))
plt.plot(t,s)
plt.show()
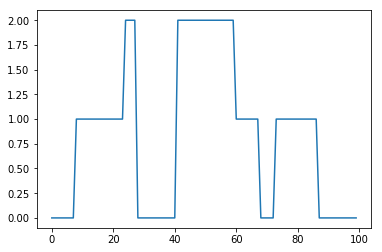
Aの値により、状態の遷移の仕方が色々変わります。今回は、いちどその状態になったら、あまり変化しないようにしてみました。このようにしてできたsをプロットしてみると以下のようになりました。
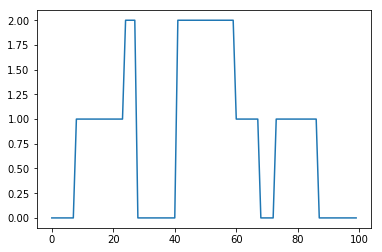
ポアソン分布のパラメータλを生成
次に、各カテゴリのポアソン分布のパラメータλを、事前分布のガンマ分布より生成します。こちらも、本当は確率的に生成する必要がありますが、端折って確率が最大になるλ(整数)を選択してしまうことにします。
# 事前分布のパラメータa,bを、カテゴリーごとに決め打ち
a = [20, 450, 1200]
b = [4, 15, 20]
lam=[0]*3
for i in range(len(a)):
lna = 0
#本当はガンマ関数ですが、aを整数に限ることにして階乗で計算
for j in range(1, a[i]): lna+=math.log(j)
lncg = a[i]*math.log(b[i])-lna
pmax=0
for j in range(1, 100):
lnp = lncg+(a[i]-1)*math.log(j)-b[i]*j
p=math.exp(lnp)
if p>pmax:
pmax=p
lam[i] = j
print(lam)
λ=[5, 30, 60]
のように生成されました。ポアソン分布の期待値はλなので、λ=5、30のときのポアソン分布は以下のようになります。(ここはコードには書いてありません)
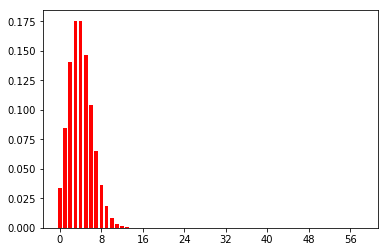
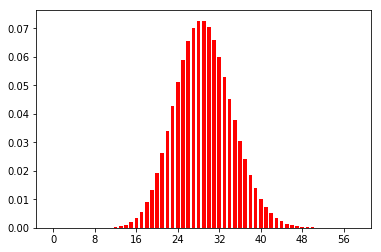
サンプルxの生成
最後に、各時系列のカテゴリ(潜在変数)と、各カテゴリのパラメータλにより、ポアソン分布でサンプルxを生成してプロットしてみます。(先ほど生成したカテゴリと並べてみます)
x = []
for i in range(len(s)):
while True:
x_tmp = random.randint(0,100)
p=lam[s[i]]**x_tmp/math.factorial(x_tmp)*np.exp(-lam[s[i]])
r = random.random()
if r<=p:
x.append(x_tmp)
break
plt.plot(t,s)
plt.show()
plt.plot(t,x)
plt.show()
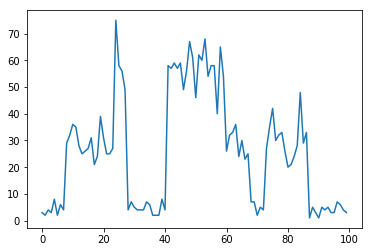
このような感じで、カテゴリとポアソン分布に基づいて、データが生成できました。※カテゴリのプロットとの対応が分かりやすいように、恣意的にλの値を生成しましたので(カテゴリが小さい=λが小さい)λの値によってはもちろんこのようにはなりません。
次はこのサンプルデータを、パラメータは未知として推論してみることにします。