概要
有限要素法を使って解析したいと思ったときは既存のソルバーを使うことが一般的だと思います。
ソルバー内部の処理はブラックボックス化されているため、内部の処理を知らなくても
解析を行うことが可能です。
しかし、技術者なら内部がどんな処理をしているのか知りたいと思うこともあると思います。
そこで、今回は解析の内部の処理をpythonで実装してみて、どんな処理が実装されているのか確かめてみようと思います。
ただ、解析にも様々な種類があるので、今回は構造解析でよく用いられる6面体要素の弾塑性解析を実装してみます。
そして、処理があっているかAbaqusを使用して検証してみます。
また、実装にはPythonを用います。
Pythonを使う理由としては、数値計算のライブラリが豊富で
行列の演算の処理を書きやすいことや、ライブラリの計算精度や処理時間も
申し分ない性能なので、今回のような実験的なコードを書くのに適していると感じたためです。
全体の処理
解く非線形方程式
今回の有限要素法では下記の非線形方程式を解くことが目的になります。
\boldsymbol{Q}(\tilde{\boldsymbol{U}}) = \boldsymbol{f} \\
\begin{align}
&\boldsymbol{Q}(\tilde{\boldsymbol{U}}) : 内力ベクトル \\
&\boldsymbol{f} : 等価節点力 \\
&\tilde{\boldsymbol{U}} : 全節点の変位をまとめたベクトル
\end{align}
ここで、$\boldsymbol{Q}(\tilde{\boldsymbol{U}})$、$\boldsymbol{f}$は下記のように表されます。
\boldsymbol{Q}(\tilde{\boldsymbol{U}}) = \sum_e \boldsymbol{q_e}(\tilde{\boldsymbol{u}}) \\
\boldsymbol{f} = \sum_e \boldsymbol{f_e} \\
\boldsymbol{q_e}(\tilde{\boldsymbol{u}}) = \boldsymbol{f_e} \\
\begin{align}
&\boldsymbol{q_e} : 要素内力ベクトル \\
&\boldsymbol{f_e} : 要素の等価節点力
\end{align}
また、$\boldsymbol{q_e}$は下記のように表されます。
\boldsymbol{q_e}(\tilde{\boldsymbol{u}}) = \int_v \boldsymbol{B}^T \sigma (\tilde{\boldsymbol{u}}) dV \\
\begin{align}
&\boldsymbol{B} : Bマトリクス \\
& \sigma : 要素内の応力
\end{align}
導出についていは下記の記事を参照ください。
有限要素法の弾塑性解析をPythonで実装する(1次元トラス要素)
ニュートン・ラプソン法
非線形方程式を解くためにニュートン・ラプソン法を使用します。
残差力ベクトルを下記のように定義し、ニュートン・ラプソン法で残差力が$0$になる$\tilde{\boldsymbol{U}}$を求めます。
\boldsymbol{R}(\tilde{\boldsymbol{U}}) = \boldsymbol{Q}(\tilde{\boldsymbol{U}}) - \boldsymbol{f} \\
\boldsymbol{R} : 残差力ベクトル
収束演算は下記のように計算することができます。
\tilde{\boldsymbol{U}}_{i+1} = \tilde{\boldsymbol{U}}_{i} + \Delta \tilde{\boldsymbol{U}} \\
\Delta \tilde{\boldsymbol{U}} = - \boldsymbol{K_t}^{-1}(\tilde{\boldsymbol{U}}_{i}) \boldsymbol{R}(\tilde{\boldsymbol{U}}_{i}) \\
\boldsymbol{K_t}(\tilde{\boldsymbol{U}}_{i}) = \frac{\partial \boldsymbol{Q}}{\partial \tilde{\boldsymbol{U}}}(\tilde{\boldsymbol{U}}_{i}) \\
\quad \\
\boldsymbol{K_t} : 接線剛性マトリクス
また、接線剛性マトリクスは下記の式で求めることができます。
\boldsymbol{K_t}(\tilde{\boldsymbol{U}}_{i}) = \sum_e \boldsymbol{K_{et}}(\tilde{\boldsymbol{u}}_{i}) \\
\boldsymbol{K_{et}}(\tilde{\boldsymbol{u}}_{i}) = \frac{\partial \boldsymbol{q_e}}{\partial \tilde{\boldsymbol{u}}}(\tilde{\boldsymbol{u}}_{i}) \\
\boldsymbol{K_{et}} : 要素接線剛性マトリクス
ここで、六面体要素の要素接線剛性マトリクスは下記の式で表されます。
\boldsymbol{K_{et}} = \int_v \boldsymbol{B}^T \boldsymbol{D} \boldsymbol{B} dV
\\
\boldsymbol{D} : Dマトリクス
全体の処理の流れ
一般的な弾塑性解析では増分解法を用いた解析が行われます。
増分解法では荷重もしくは強制変位を幾つかに分割し、段階的に荷重を負荷させて、変位、ひずみ、応力などを求める手法です。Abaqusではこの分割をインクリメントと呼んでいるので、本稿でもインクリメントと呼ぶことにします。
ここで、解析の全体の処理の流れを下記に示します。
①. 荷重をインクリメント毎に分割する。(今回は等分割)
②. 変位$\tilde{\boldsymbol{U}}$を初期化する。
\tilde{\boldsymbol{U}} = \boldsymbol{0}
③. $i$インクリメントの残差力$\boldsymbol{R}$を初期化する。
\boldsymbol{R} = \boldsymbol{f}^{i} - \boldsymbol{f}^{i-1} \\
\boldsymbol{f}^i : iインクリメントの荷重
④. 接線剛性マトリクス$\boldsymbol{K_t}$を計算する。
\boldsymbol{K_t} = \sum_e \boldsymbol{K_{et}} \\
⑤. 接線剛性マトリクス$\boldsymbol{K_t}$と残差力$\boldsymbol{R}$に境界条件の処理を行う。
⑥. 変位の増分$\Delta \tilde{\boldsymbol{U}}$を求めて、変位$\tilde{\boldsymbol{U}}$を更新する。
\Delta \tilde{\boldsymbol{U}} = -\boldsymbol{K_t}^{-1} \boldsymbol{R}(\tilde{\boldsymbol{U}}_{i}) \\
\tilde{\boldsymbol{U}}_{j+1} = \tilde{\boldsymbol{U}}_j + \Delta \tilde{\boldsymbol{U}}
⑦. 要素のひずみを計算する。
\epsilon = \boldsymbol{B}\tilde{\boldsymbol{U}}
⑧. リターンマッピング法により、要素の塑性ひずみ$\epsilon_p$、応力$\sigma$などを求める。
⑨. 内力ベクトルを計算する。
\boldsymbol{Q}= \sum_e \boldsymbol{q_e} \\
\boldsymbol{q_e} = \int_v \boldsymbol{B}^T \sigma dV
⑩. 残差力$\boldsymbol{R}$を計算する。
\boldsymbol{R} = \boldsymbol{Q} - \boldsymbol{f}^i
⑪. 収束判定を行う。
収束判定を満たしていなければ④に戻る。
⑫. インクリメントが最後の場合は処理を終了する。そうでなければ、$i = i+1$として③に戻る。
上記の収束演算の一回の試行をイテレーションと呼ぶことにします。
そして、収束演算は1次元の変位の図で記載すると下記のように表すことができます。

リターンマッピング法
リターンマッピング法は要素が塑性変形中は必ず降伏関数が0になるという条件のもとで塑性ひずみと応力を求めるアルゴリズムです。
ここで、材料の1軸での応力、ひずみ関係は下記のように多直線で近似されているとします。
3次元のリターンマッピング法では、偏差応力$\boldsymbol{s}$と相当塑性ひずみ$\bar{\epsilon}_p$を使って降伏関数$f$を下記のように定義します。
\begin{align}
&f(\boldsymbol{s}, \bar{\epsilon}_p) = ||\boldsymbol{s}||_F - \sqrt{\frac{2}{3}}k(\bar{\epsilon}_p) \tag{1}\\
&k(\bar{\epsilon}_p) : \bar{\epsilon}_pのときの降伏応力
\end{align}
ここで、$||\boldsymbol{s}||_F$は行列$\boldsymbol{s}$のフロベニウスノルムになります。
また、偏差応力$\boldsymbol{s}$、相当塑性ひずみ$\bar{\epsilon}_p$は下記の式で定義されます。
\boldsymbol{s} =
\begin{bmatrix}
\sigma_{xx} - \sigma_{m} && \sigma_{xy} && \sigma_{xz} \\
\sigma_{xy} && \sigma_{yy} - \sigma_{m} && \sigma_{yz} \\
\sigma_{xz} && \sigma_{yz} &&\sigma_{zz} - \sigma_{m}
\end{bmatrix}
\\
\sigma_m = \frac{1}{3}(\sigma_{xx} + \sigma_{yy} + \sigma_{zz}) \\
\sigma_m : 静水圧応力
\begin{align}
\bar{\epsilon}_p = \int_0^t \dot{\bar{\epsilon}}_p dt \tag{2} \\
\dot{\bar{\epsilon}}_p = \sqrt{\frac{2}{3}} || \dot{\epsilon}_p||_F \tag{3} \\
\dot{\bar{\epsilon}}_p : 相当塑性ひずみ速度 \\
\dot{\epsilon}_p : 塑性ひずみ速度
\end{align}
偏差応力はテンソルですが、行列としても処理に影響はないので、ここでは行列として扱います。
ここで、流れ則の理論によると、下記の式が定義されます。
\begin{align}
\dot{\epsilon}_p = \dot{\gamma} \frac{\partial f}{\partial \boldsymbol{s}} \tag{4}
\end{align}
\\
\dot{\epsilon}_p : 塑性ひずみ速度 \\
\dot{\gamma} : 塑性乗数
$\dot{\gamma}$は塑性乗数と言われ、$\dot{\gamma} \geq 0$となります。
降伏関数の偏差応力に関する偏微分は計算すると下記の式のようになります。
\begin{align}
\frac{\partial f}{\partial \boldsymbol{s}} = \frac{\boldsymbol{s}}{||\boldsymbol{s}||_F} \tag{5}
\end{align}
これを流れ則の式(4)に代入すると、下記の式のようになります。
\begin{align}
\dot{\epsilon}_p = \dot{\gamma} \frac{\boldsymbol{s}}{||\boldsymbol{s}||_F} \tag{6}\\
\end{align}
この式を使うと、相当塑性ひずみ速度は下記の式で表すことができます。
\begin{align}
\dot{\bar{\epsilon}}_p = \sqrt{\frac{2}{3}} || \dot{\epsilon}_p||_F =
\sqrt{\frac{2}{3}}|| (\dot{\gamma} \frac{\boldsymbol{s}}{||\boldsymbol{s}||_F}) ||_F =
\sqrt{\frac{2}{3}} \dot{\gamma} \tag{7}
\end{align}
ここで、$||\frac{\boldsymbol{s}}{||\boldsymbol{s}||_F}||_F$は$1$なので、消去することができます。
ここで、後退Euler法により、$i+1$番目の相当塑性ひずみを下記のように定義します。
\begin{align}
\bar{\epsilon}_{p, i+1} = \bar{\epsilon}_{p, i} + \dot{\bar{\epsilon}}_{p, i+1} \Delta t \tag{8}
\end{align}
\\
\Delta t : iからi+1の間の時間
先ほどの塑性ひずみ速度の式(7)を代入すると、下記のように表せます。
\begin{align}
\bar{\epsilon}_{p, i+1} &= \bar{\epsilon}_{p, i} + \sqrt{\frac{2}{3}} \dot{\gamma}_{i+1} \Delta t \\
&= \bar{\epsilon}_{p, i} + \sqrt{\frac{2}{3}} \Delta \gamma_{i+1} \tag{9}
\end{align}
\\
\Delta\gamma_{i+1} = \dot{\gamma}_{i+1} \Delta t
また、同じく後退Euler法により、$i+1$番目の塑性ひずみを定義することができます。
\begin{align}
\boldsymbol{\epsilon}_{p, i+1} &= \boldsymbol{\epsilon}_{p, i} + \dot{\boldsymbol{\epsilon}}_{p, i+1} \Delta t \\
&= \boldsymbol{\epsilon}_{p, i} + \dot{\gamma}_{i+1} \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} \Delta t \\
&= \boldsymbol{\epsilon}_{p, i} + \dot{\gamma}_{i+1} \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} \Delta t
\\
&= \boldsymbol{\epsilon}_{p, i} + \Delta\gamma_{i+1} \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} \tag{10}
\end{align}
次に、偏差応力は下記の式で表せるという特徴があります。
\begin{align}
\boldsymbol{s} = 2G(\boldsymbol{e} - \boldsymbol{\epsilon}_p) \tag{11}
\end{align}
\\
G : 横弾性係数 \\
\boldsymbol{e} : 偏差ひずみ \\
\boldsymbol{\epsilon}_p : 塑性ひずみ
偏差ひずみは下記の式で定義されます。
\boldsymbol{e} =
\begin{bmatrix}
\epsilon_{xx} - \epsilon_{m} && \epsilon_{xy} && \epsilon_{xz} \\
\epsilon_{xy} && \epsilon_{yy} - \epsilon_{m} && \epsilon_{yz} \\
\epsilon_{xz} && \epsilon_{yz} && \epsilon_{zz} - \epsilon_{m} \\
\end{bmatrix}
\\
\epsilon_m = \frac{1}{3}(\epsilon_{xx} + \epsilon_{yy} + \epsilon_{zz})
\\
ここで、i+1番目の試行応力$\boldsymbol{s}^{tri}_{i+1}$を下記のように定義します。
\begin{align}
\boldsymbol{s}^{tri}_{i+1} = \boldsymbol{s}_i + 2G(\boldsymbol{e}_{i+1} - \boldsymbol{e}_i) \tag{12}
\end{align}
そして、i+1番目の偏差応力を式変形してみます。
\begin{align}
\boldsymbol{s}_{i+1} &= 2G(\boldsymbol{e}_{i+1} - \boldsymbol{\epsilon}_{p,i+1}) \\
&= 2G(\boldsymbol{e}_{i+1} - \boldsymbol{e}_i + \boldsymbol{e}_i - \boldsymbol{\epsilon}_{p,i+1}) \\
&= 2G(\boldsymbol{e}_{i+1} - \boldsymbol{e}_i) + 2G(\boldsymbol{e}_i - \boldsymbol{\epsilon}_{p,i+1}) \\
&= \boldsymbol{s}^{tri}_{i+1} - \boldsymbol{s}_i + 2G \{ \boldsymbol{e}_i - \boldsymbol{\epsilon}_{p, i} - \Delta\gamma_{i+1} \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} \\
&= \boldsymbol{s}^{tri}_{i+1} - \boldsymbol{s}_i + 2G(\boldsymbol{e}_i - \boldsymbol{\epsilon}_{p, i}) - 2G \Delta\gamma_{i+1} \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} \\
&= \boldsymbol{s}^{tri}_{i+1} - \boldsymbol{s}_i + \boldsymbol{s}_i - 2G \Delta\gamma_{i+1} \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} \\
&= \boldsymbol{s}^{tri}_{i+1} - 2G \Delta\gamma_{i+1} \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} \tag{13}
\end{align}
ここで、式を下記のように変形してみます。
\begin{align}
||\boldsymbol{s}_{i+1}||_F \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} = ||\boldsymbol{s}^{tri}_{i+1}|| _F\frac{\boldsymbol{s}^{tri}_{i+1}}{||\boldsymbol{s}^{tri}_{i+1}||_F} - 2G \Delta\gamma_{i+1} \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} \\
(||\boldsymbol{s}_{i+1}||_F + 2G \Delta\gamma_{i+1}) \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} = ||\boldsymbol{s}^{tri}_{i+1}||_F \frac{\boldsymbol{s}^{tri}_{i+1}}{||\boldsymbol{s}^{tri}_{i+1}||_F} \tag{14}
\end{align}
ここで、$\Delta\gamma_{i+1}$は前の定義より必ず0以上なので、式(14)は$(||\boldsymbol{s}_{i+1}||_F + 2G \Delta\gamma_{i+1}) \geq 0$, $||\boldsymbol{s}^{tri}_{i+1}||_F \geq 0$となります。
そのため、下記の式が成り立ちます。
\begin{align}
\frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} = \frac{\boldsymbol{s}^{tri}_{i+1}}{||\boldsymbol{s}^{tri}_{i+1}||_F} \tag{15}\\
||\boldsymbol{s}_{i+1}||_F = ||\boldsymbol{s}^{tri}_{i+1}||_F - 2G \Delta\gamma_{i+1} \tag{16}
\end{align}
ここで、求まった$||\boldsymbol{s}_{i+1}||_F$(式(16))と$\boldsymbol{\epsilon}_{p, i+1}$(式(9))を降伏関数(式(1))に代入してみます。
\begin{align}
f(\boldsymbol{s}_{i+1}, \bar{\epsilon}_{p,i+1}) &= ||\boldsymbol{s}_{i+1}||_F - \sqrt{\frac{2}{3}}k(\bar{\epsilon}_{p,i+1}) \\
&= ||\boldsymbol{s}^{tri}_{i+1}||_F - 2G \Delta\gamma_{i+1} - \sqrt{\frac{2}{3}}k(\bar{\epsilon}_{p, i} + \sqrt{\frac{2}{3}} \Delta\gamma_{i+1}) \tag{17}
\end{align}
ここで、式(17)の右辺の第3項を1次のテイラー展開で近似します。
\begin{align}
k(\bar{\epsilon}_{p, i} + \sqrt{\frac{2}{3}} \Delta\gamma_{i+1}) \approx k(\bar{\epsilon}_{p, i} ) + \sqrt{\frac{2}{3}} \Delta\gamma_{i+1} k'(\bar{\epsilon}_{p, i})
\tag{18}
\end{align}
\\
k' : kの一次微分
次に下記のように$f^{tri}_{i+1}$を定義します。
\begin{align}
f^{tri}_{i+1} = f(\boldsymbol{s}^{tri}_{i+1}, \bar{\epsilon}_{p,i})
= ||\boldsymbol{s}^{tri}_{i+1}||_F - \sqrt{\frac{2}{3}}k(\bar{\epsilon}_{p,i}) \tag{19}
\end{align}
式(17)に式(18)、(19)を代入すると下記の式が得られます。
\begin{align}
f(\boldsymbol{s}_{i+1}, \bar{\epsilon}_{p,i+1}) &= ||\boldsymbol{s}^{tri}_{i+1}||_F - 2G \Delta\gamma_{i+1} - \sqrt{\frac{2}{3}}k(\bar{\epsilon}_{p, i} + \sqrt{\frac{2}{3}} \Delta\gamma_{i+1}) \\
&= ||\boldsymbol{s}^{tri}_{i+1}||_F - \sqrt{\frac{2}{3}}k(\bar{\epsilon}_{p, i})- 2G \Delta\gamma_{i+1} - \frac{2}{3} \Delta\gamma_{i+1} k'(\bar{\epsilon}_{p, i}) \\
&= f^{tri}_{i+1} - 2G\Delta\gamma_{i+1} - \frac{2}{3} \Delta\gamma_{i+1} k'(\bar{\epsilon}_{p, i}) \tag{20}
\end{align}
式(20)より、弾性変形のとき($\Delta\gamma_{i+1} = 0$)は、$f(\boldsymbol{s}_{i+1}, \bar{\epsilon}_{p,i+1}) = f^{tri}_{i+1} $となります。また、塑性変形のとき($\Delta\gamma_{i+1} > 0$)は$f(\boldsymbol{s}_{i+1}, \bar{\epsilon}_{p,i+1}) < f^{tri}\_{i+1} $となるため、$f^{tri}\_{i+1} > 0$となります。
そのため、$f^{tri}_{i+1}$が0より大きいか小さいかで弾性変形か塑性変形かの判断をすることができます。
ただし、上記の判断は軟化する場合($k' < 0$)では成り立たないことに注意が必要です。
そして、塑性変形だった場合は、$\Delta\gamma_{i+1}$を求める必要があります。
塑性変形の際は式(17)が0となるので、
\begin{align}
f(\boldsymbol{s}_{i+1}, \bar{\epsilon}_{p,i+1}) &= ||\boldsymbol{s}^{tri}_{i+1}||_F - 2G \Delta\gamma_{i+1} - \sqrt{\frac{2}{3}}k(\bar{\epsilon}_{p, i} + \sqrt{\frac{2}{3}} \Delta\gamma_{i+1}) = 0 \tag{21}
\end{align}
式(21)を満たす$\Delta\gamma_{i+1}$を求めます。ただ、式(21)は非線形方程式なので、求めるのにニュートン・ラプソン法を用います。
ここで、ニュートン・ラプソン法では$f(x) = 0$となる解は下記のように収束演算で求めることができます。
x_0 = 0 \\
x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} \\
x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} \\
\vdots \\
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
$f(x_n) < tol(tol : 収束判定のパラメータ)$のとき、収束したとみなして、$x = x_n$とします。
これと全く同じ操作を行えば求めることが可能です。
f(\Delta \gamma_{i+1}) = ||\boldsymbol{s}^{tri}_{i+1}||_F - 2G \Delta\gamma_{i+1} - \sqrt{\frac{2}{3}}k(\bar{\epsilon}_{p, i} + \sqrt{\frac{2}{3}} \Delta\gamma_{i+1}) \\
f'(\Delta \gamma_{i+1}) = -2G - \sqrt{\frac{2}{3}} k'(\bar{\epsilon}_{p, i} + \sqrt{\frac{2}{3}} \Delta\gamma_{i+1})
最後に偏差応力を元の応力に戻す方法ですが、リターンマッピング法により静水圧応力$\sigma_m$は変化しないという特徴があるため、下記の式で求めることが可能です。
\boldsymbol{\sigma}_{i+1} = \boldsymbol{s}_{i+1} + \sigma_m \boldsymbol{I}_3 \\
\sigma_m = K \epsilon_m \\
\epsilon_m = \frac{1}{3}(\epsilon_{xx, i+1} + \epsilon_{yy, i+1} + \epsilon_{zz, i+1})
\\
K : 体積弾性率
定式化は以上になります。最後に処理をまとめてみます。
① 試行応力$\boldsymbol{s}^{tri}_{i+1}$を計算する
\boldsymbol{s}^{tri}_{i+1} = \boldsymbol{s}_i + 2G(\boldsymbol{e}_{i+1} - \boldsymbol{e}_{p,i})
② $f^{tri}_{i+1}$を計算する
f^{tri}_{i+1} = f(\boldsymbol{s}^{tri}_{i+1}, \bar{\epsilon}_{i,p})
= ||\boldsymbol{s}^{tri}_{i+1}||_F - \sqrt{\frac{2}{3}}k(\bar{\epsilon}_{p,i})
③ $f^{tri}_{i+1} \leq 0$ならば$\Delta \gamma = 0$、$f^{tri}_{i+1} > 0$ならばニュートン・ラプソン法で下記の式を満たす$\Delta \gamma$を計算する
f(\boldsymbol{s}_{i+1}, \bar{\epsilon}_{p,i+1}) =
||\boldsymbol{s}^{tri}_{i+1}||_F - 2G \Delta\gamma_{i+1} - \sqrt{\frac{2}{3}}k(\bar{\epsilon}_{p, i} + \sqrt{\frac{2}{3}} \Delta\gamma_{i+1}) = 0
④塑性ひずみ$\boldsymbol{\epsilon}_{p, i+1}$と相当塑性ひずみ$\bar{\epsilon}_{p, i+1}$と偏差応力$\boldsymbol{s}_{i+1}$を計算する
\boldsymbol{s}_{i+1} = \boldsymbol{s}^{tri}_{i+1} - 2G \Delta\gamma_{i+1} \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} \\
\boldsymbol{\epsilon}_{p, i+1} = \boldsymbol{\epsilon}_{p, i} + \Delta\gamma_{i+1} \frac{\boldsymbol{s}_{i+1}}{||\boldsymbol{s}_{i+1}||_F} \\
\bar{\epsilon}_{p, i+1} = \bar{\epsilon}_{p, i} + \sqrt{\frac{2}{3}} \Delta\gamma_{i+1}
⑤応力$\boldsymbol{\sigma}_{i+1}$を計算する
\boldsymbol{\sigma}_{i+1} = \boldsymbol{s}_{i+1} + \sigma_m \boldsymbol{I}_3
整合接線係数
弾性状態では応力とひずみは下記の式で表すことができます。
\boldsymbol{\sigma} = \boldsymbol{D} \boldsymbol{\epsilon} \\
\boldsymbol{D} =
\frac{E}{(1+\nu)(1-2\nu)}
\begin{bmatrix}
1-\nu && \nu && \nu && 0 && 0 && 0 \\
\nu && 1-\nu && \nu && 0 && 0 && 0 \\
\nu && \nu && 1-\nu && 0 && 0 && 0 \\
0 && 0 && 0 && \frac{1-2\nu}{2} && 0 && 0 \\
0 && 0 && 0 && 0 && \frac{1-2\nu}{2} && 0 \\
0 && 0 && 0 && 0 && 0 && \frac{1-2\nu}{2}
\end{bmatrix}
ここで、$\boldsymbol{D}$は無限小の$\boldsymbol{\sigma}$と$\boldsymbol{\epsilon}$の偏微分として下記のように表されます。
\boldsymbol{D} = \frac{\partial \boldsymbol{\sigma}}{\partial \boldsymbol{\epsilon}}
しかし、リターンマッピング法では弾塑性状態の時に$\boldsymbol{\sigma}_{i+1}$と$\boldsymbol{\epsilon}_{i+1}$を降伏関数が0になるという条件のもとで求めました。
そのため、塑性状態のときはDマトリクスを下記の式で求められる整合接線係数$\boldsymbol{D}_{ep}$に置き換えます。
\boldsymbol{D}_{ep} = \frac{\partial \boldsymbol{\sigma}_{i+1}}{\partial
\boldsymbol{\epsilon}_{i+1}}
この式は微小な$\delta \boldsymbol{\sigma}_{i+1}$と$\delta \boldsymbol{\epsilon}_{i+1}$をリターンマッピングの式から求め、除算することで求めることができます。
この式の導出過程は複雑になるので、ここでは結果だけ示すことにします。
書籍「計算破壊力学のための応用有限要素法プログラム実装」によると、整合接線係数$\boldsymbol{D}_{ep}$は下記の式で求めることが可能です。
\boldsymbol{D}_{ep} = \boldsymbol{A} - \frac{\boldsymbol{A} \{ \boldsymbol{\sigma}' \} \{ \boldsymbol{\sigma}'\}^T \boldsymbol{A}}{\frac{4}{9} a k'(\bar{\epsilon}_{p, i}) \bar{\sigma}^2 + \{ \boldsymbol{\sigma}'\}^T \boldsymbol{A} \{\boldsymbol{\sigma}'\}} \\
\boldsymbol{A} = (\boldsymbol{D}^{-1} + \gamma' \boldsymbol{P})^{-1} \\
\{\boldsymbol{\sigma}'\} = \boldsymbol{P} \{ \boldsymbol{\sigma}_i \} \\
\gamma' = \frac{3(\bar{\epsilon}_{p, i+1} - \bar{\epsilon}_{p, i})}{2\bar{\sigma}} \\
a = (1 - \frac{2}{3} \gamma' k'(\bar{\epsilon}_{p, i}))^{-1} \\
\bar{\sigma} = \sqrt{\frac{3}{2}||\boldsymbol{s}_i||_F} \qquad : ミーゼス応力 \\
\boldsymbol{P} =
\frac{1}{3}
\begin{bmatrix}
2 && -1 && -1 && 0 && 0 && 0 \\
-1 && 2 && -1 && 0 && 0 && 0 \\
-1 && -1 && 2 && 0 && 0 && 0 \\
0 && 0 && 0 && 6 && 0 && 0 \\
0 && 0 && 0 && 0 && 6 && 0 \\
0 && 0 && 0 && 0 && 0 && 6 \\
\end{bmatrix}
\\
\{\boldsymbol{\sigma}_i\}
=
\begin{bmatrix}
\sigma_{xx,i} \\
\sigma_{yy,i} \\
\sigma_{zz,i} \\
\sigma_{yz,i} \\
\sigma_{xz,i} \\
\sigma_{xy,i}
\end{bmatrix}
リターンマッピング法をPythonで実装する
上記のリターンマッピング法の処理をPythonで実装します。
この処理を実装するためにDマトリクスを計算するクラスDmatrixを用意します。
Dmatrix.py
import numpy as np
# Dマトリクスを計算するためのクラス
class Dmatrix:
# コンストラクタ
# young : ヤング率
# poisson : ポアソン比
def __init__(self, young, poisson):
self.young = young
self.poisson = poisson
# 弾性状態のDマトリクスを作成する
def makeDematrix(self):
tmp = self.young / ((1.0 + self.poisson) * (1.0 - 2.0 * self.poisson))
matD = np.array([[1.0 - self.poisson, self.poisson, self.poisson, 0.0, 0.0, 0.0],
[self.poisson, 1.0 - self.poisson, self.poisson, 0.0, 0.0, 0.0],
[self.poisson, self.poisson, 1.0 - self.poisson, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.5 * (1.0 - 2.0 * self.poisson), 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.5 * (1.0 - 2.0 * self.poisson), 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.5 * (1.0 - 2.0 * self.poisson)]])
matD = tmp * matD
return matD
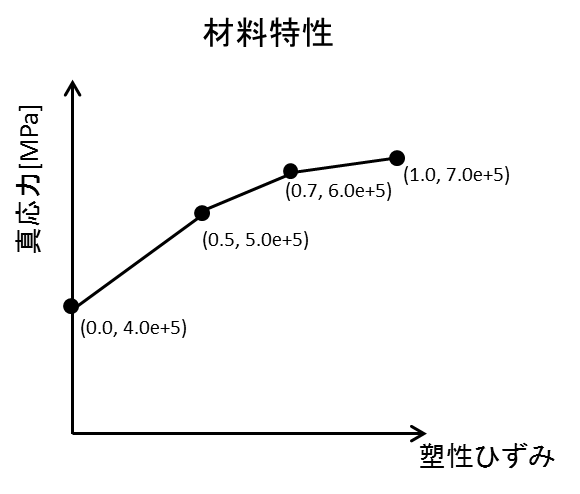
リターンマッピング法と整合接線係数を計算するためにMisesMaterialクラスを実装します。材料情報として1軸の塑性ひずみ、真応力を下記の図のようにポイントで入力します。入力はaddStressPStrainLine関数で塑性ひずみが昇順になる順番で入力します。リターンマッピング法の計算はreturnMapping3D関数で行い、応力と各ひずみに加えて整合接線係数を返すようにしています。その他の関数は上記の関数を計算するために用意しています。

MisesMaterial.py
import numpy as np
import numpy.linalg as LA
from Dmatrix import Dmatrix
# Misesモデルの構成則を計算するためのクラス
class MisesMaterial:
# コンストラクタ
# young : ヤング率
# poisson : ポアソン比
def __init__(self, young, poisson):
# インスタンス変数を定義する
self.young = young # ヤング率
self.poisson = poisson # ポアソン比
self.G = young / (2.0 * (1.0 + poisson)) # 横弾性係数
self.K = young / (3.0 * (1.0 - 2.0 * poisson)) # 体積弾性率
self.stressLine = [] # 真応力-塑性ひずみ多直線の真応力データ
self.pStrainLine = [] # 真応力-塑性ひずみ多直線の塑性ひずみデータ
self.itrNum = 100 # ニュートン・ラプソン法の収束回数の上限
self.tol = 1.0e-6 # ニュートン・ラプソン法の収束基準
# 真応力-塑性ひずみ多直線のデータを追加する
# (入力されるデータはひずみが小さい順になり、最初の塑性ひずみは0.0にならなければいけない)
# (塑性係数は正になる前提)
# stress : 真応力
# pStrain : 塑性ひずみ
def addStressPStrainLine(self, stress, pStrain):
# 入力チェック
if len(self.pStrainLine) == 0:
if not pStrain == 0.0 :
raise ValueError("応力-ひずみ多直線データの最初のひずみは0.0になる必要があります。")
elif self.pStrainLine[-1] > pStrain:
raise ValueError("応力-ひずみ多直線データの入力順序が間違っています。")
# 最初の入力の場合は降伏応力を格納する
if len(self.stressLine) == 0:
self.yieldStress = stress # 降伏応力
self.stressLine.append(stress)
self.pStrainLine.append(pStrain)
# 降伏関数を計算する
# mStress : 相当応力
# ePStrain : 相当塑性ひずみ
def yieldFunction(self, mStress, ePStrain):
f = 0.0
if hasattr(self, 'yieldStress'):
f = mStress - self.makeYieldStress(ePStrain)
return f
# 降伏応力を求める
# ePStrain : 相当塑性ひずみ
def makeYieldStress(self, ePStrain):
yieldStress = 0.0
if hasattr(self, 'yieldStress'):
# pStrainが何番目のデータの間か求める
no = None
for i in range(len(self.pStrainLine) - 1):
if self.pStrainLine[i] <= ePStrain and ePStrain <= self.pStrainLine[i+1]:
no = i
break
if no is None :
raise ValueError("相当塑性ひずみが定義した範囲を超えています。")
hDash = self.makePlasticModule(ePStrain)
yieldStress = hDash * (ePStrain - self.pStrainLine[no]) + self.stressLine[no]
return yieldStress
# 塑性係数を求める
# ePStrain : 相当塑性ひずみ
def makePlasticModule(self, ePStrain):
# epが何番目のデータの間か求める
no = None
for i in range(len(self.pStrainLine) - 1):
if self.pStrainLine[i] <= ePStrain and ePStrain <= self.pStrainLine[i+1]:
no = i
if no is None :
raise ValueError("相当塑性ひずみが定義した範囲を超えています。")
# 塑性係数を計算する
h = (self.stressLine[no+1] - self.stressLine[no]) / (self.pStrainLine[no+1] - self.pStrainLine[no])
return h
# Return Mapping法により、3次元の応力、塑性ひずみ、相当塑性ひずみ、降伏判定を計算する
# vecStrain : 全ひずみ
# vecPrevPStrain : 前回の塑性ひずみ
# prevEPStrain : 前回の相当塑性ひずみ
def returnMapping3D(self, vecStrain, vecPrevPStrain, prevEPStrain):
# 偏差ひずみのテンソルを求める
mStrain = (1.0 / 3.0) * (vecStrain[0] + vecStrain[1] + vecStrain[2])
tenStrain = np.array([[vecStrain[0], vecStrain[5] * 0.5, vecStrain[4] * 0.5],
[vecStrain[5] * 0.5, vecStrain[1], vecStrain[3] * 0.5],
[vecStrain[4] * 0.5, vecStrain[3] * 0.5, vecStrain[2]]])
tenDStrain = tenStrain - mStrain * np.eye(3)
# 前回の塑性ひずみのテンソルを求める
tenPrevPStrain = np.array([[vecPrevPStrain[0], vecPrevPStrain[5] * 0.5, vecPrevPStrain[4] * 0.5],
[vecPrevPStrain[5] * 0.5, vecPrevPStrain[1], vecPrevPStrain[3] * 0.5],
[vecPrevPStrain[4] * 0.5, vecPrevPStrain[3] * 0.5, vecPrevPStrain[2]]])
# 試行弾性偏差応力のテンソルを求める
tenTriDStress = 2.0 * self.G * (tenDStrain - tenPrevPStrain)
# 試行弾性応力のミーゼス応力を求める
mTriStress = np.sqrt(3.0 / 2.0) * LA.norm(tenTriDStress, "fro")
# 降伏関数を計算する
triF = self.yieldFunction(mTriStress, prevEPStrain)
# 降伏判定を計算する
if triF > 0.0:
yieldFlg = True
else:
yieldFlg = False
# ΔGammaをニュートン・ラプソン法で計算する
deltaGamma = 0.0
if triF > 0.0 :
normTriDStress = LA.norm(tenTriDStress, "fro")
# 収束演算を行う
for i in range(self.itrNum):
# yを計算する
yieldStress = self.makeYieldStress(prevEPStrain + np.sqrt(2.0 / 3.0) * deltaGamma)
y = normTriDStress - 2.0 * self.G * deltaGamma - np.sqrt(2.0 / 3.0) * yieldStress
# y'を計算する
hDash = self.makePlasticModule(prevEPStrain + np.sqrt(2.0 / 3.0) * deltaGamma)
yDash = - 2.0 * self.G - (2.0 / 3.0) * hDash
# 収束判定を行う
if np.abs(y) < self.tol:
break
elif (i + 1) == self.itrNum:
raise ValueError("ニュートン・ラプソン法が収束しませんでした。")
# ΔGammaを更新する
deltaGamma -= y / yDash
# ΔGammaの値をチェックする
if deltaGamma < 0:
raise ValueError("ΔGammaが負になりました。")
# テンソルNを計算する
tenN = tenTriDStress / LA.norm(tenTriDStress, "fro")
# 塑性ひずみのテンソルを計算する
tenPStrain = tenPrevPStrain + tenN * deltaGamma
# 弾性ひずみのテンソルを計算する
tenEStrain = tenStrain - tenPStrain
# 応力のテンソルを計算する
vStrain = vecStrain[0] + vecStrain[1] + vecStrain[2]
mSigma = self.K * vStrain
tenDStress = 2.0 * self.G * (tenDStrain - tenPStrain)
tenStress = tenDStress + mSigma * np.eye(3)
# 相当塑性ひずみを計算する
ePStrain = prevEPStrain + np.sqrt(2.0 / 3.0) * deltaGamma
# 応力を求める
vecStress = np.array([tenStress[0,0],
tenStress[1,1],
tenStress[2,2],
tenStress[1,2],
tenStress[0,2],
tenStress[0,1]])
# 弾性ひずみを求める
vecEStrain = np.array([tenEStrain[0,0],
tenEStrain[1,1],
tenEStrain[2,2],
2.0 * tenEStrain[1,2],
2.0 * tenEStrain[0,2],
2.0 * tenEStrain[0,1]])
# 塑性ひずみを求める
vecPStrain = np.array([tenPStrain[0,0],
tenPStrain[1,1],
tenPStrain[2,2],
2.0 * tenPStrain[1,2],
2.0 * tenPStrain[0,2],
2.0 * tenPStrain[0,1]])
# 整合接線係数を求める
if yieldFlg == True:
matDep = self.makeDepmatrix3D(vecStress, ePStrain, prevEPStrain)
else:
matDep = Dmatrix(self.young, self.poisson).makeDematrix()
return vecStress, vecEStrain, vecPStrain, ePStrain, yieldFlg, matDep
# 3次元のミーゼス応力を計算する
# vecStress : 応力ベクトル(np.array型)
def misesStress3D(self, vecStress):
tmp1 = np.square(vecStress[0] - vecStress[1]) + np.square(vecStress[1] - vecStress[2]) + np.square(vecStress[2] - vecStress[0])
tmp2 = 6.0 * (np.square(vecStress[3]) + np.square(vecStress[4]) + np.square(vecStress[5]))
mises = np.sqrt(0.5 * (tmp1 + tmp2))
return mises
# 塑性状態のDマトリクスを作成する
# vecStress : 応力
# ePStrain : 相当塑性ひずみ
# prevEPStrain : 前の相当塑性ひずみ
def makeDepmatrix3D(self, vecStress, ePStrain, prevEPStrain):
# Deマトリクスを計算する
matDe = Dmatrix(self.young, self.poisson).makeDematrix()
# gammmaDashを計算する
deltaEPStrain = ePStrain - prevEPStrain
mStress = self.misesStress3D(vecStress)
gammaDash = 3.0 * deltaEPStrain / (2.0 * mStress)
matP = (1.0 / 3.0) * np.array([[2.0, -1.0, -1.0, 0.0, 0.0, 0.0],
[-1.0, 2.0, -1.0, 0.0, 0.0, 0.0],
[-1.0, -1.0, 2.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 6.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 6.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 6.0]])
matA = LA.inv(LA.inv(matDe) + gammaDash * matP)
hDash = self.makePlasticModule(ePStrain)
a = np.power(1.0 - (2.0 / 3.0) * gammaDash * hDash, -1)
vecDStress = matP @ vecStress
tmp1 = np.array(matA @ (np.matrix(vecDStress).T * np.matrix(vecDStress)) @ matA)
tmp2 = (4.0 / 9.0) * a * hDash * mStress ** 2 + (np.matrix(vecDStress) @ matA @ np.matrix(vecDStress).T)[0,0]
matDep = np.array(matA - tmp1 / tmp2)
return matDep
6面体要素
正規化座標系
6面体要素は下記のように正規化座標系に変換することが可能です。
座標変換は下記の式で表されます。
x = \sum_{i=1}^8 N_i x_i \\
y = \sum_{i=1}^8 N_i y_i \\
z = \sum_{i=1}^8 N_i z_i \\
\begin{align}
&& N_1 = \frac{(1-a)(1-b)(1-c)}{8} && N_2 = \frac{(1+a)(1-b)(1-c)}{8} \\
&& N_3 = \frac{(1+a)(1+b)(1-c)}{8} && N_4 = \frac{(1-a)(1+b)(1-c)}{8} \\
&& N_5 = \frac{(1-a)(1-b)(1+c)}{8} && N_6 = \frac{(1+a)(1-b)(1+c)}{8} \\
&& N_7 = \frac{(1+a)(1+b)(1+c)}{8} && N_8 = \frac{(1-a)(1+b)(1+c)}{8} \\
\end{align}
\begin{align}
&x_i : i節点のx座標 \\
&y_i : i節点のy座標 \\
&z_i : i節点のz座標 \\
&N_i : 形状関数
\end{align}
ヤコビ行列
座標変換のヤコビ行列は下記の式で表されます。
\boldsymbol{J}=
\begin{bmatrix}
\frac{\partial x}{\partial a} && \frac{\partial y}{\partial a} && \frac{\partial z}{\partial a} \\
\frac{\partial x}{\partial b} && \frac{\partial y}{\partial b} && \frac{\partial z}{\partial b} \\
\frac{\partial x}{\partial c} && \frac{\partial y}{\partial c} && \frac{\partial z}{\partial c}
\end{bmatrix}
\\
\begin{align}
&\frac{\partial x}{\partial a} = \sum_{i=1}^8 \frac{\partial N_i}{\partial a}x_i & \frac{\partial x}{\partial b} = \sum_{i=1}^8 \frac{\partial N_i}{\partial b}x_i & & \frac{\partial x}{\partial c} = \sum_{i=1}^8 \frac{\partial N_i}{\partial c}x_i \\
&\frac{\partial y}{\partial a} = \sum_{i=1}^8 \frac{\partial N_i}{\partial a}y_i & \frac{\partial y}{\partial b} = \sum_{i=1}^8 \frac{\partial N_i}{\partial b}y_i & & \frac{\partial y}{\partial c} = \sum_{i=1}^8 \frac{\partial N_i}{\partial c}y_i\\
&\frac{\partial z}{\partial a} = \sum_{i=1}^8 \frac{\partial N_i}{\partial a}z_i & \frac{\partial z}{\partial b} = \sum_{i=1}^8 \frac{\partial N_i}{\partial b}z_i & & \frac{\partial z}{\partial c} = \sum_{i=1}^8 \frac{\partial N_i}{\partial c}z_i\\
\end{align}
Bマトリクス
Bマトリクスは形状関数の偏微分で求めることができます。
\boldsymbol{B} =
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && 0 && 0 && \dots && \frac{\partial N_8}{\partial x} && 0 && 0 \\
0 && \frac{\partial N_1}{\partial y} && 0 && \dots && 0 && \frac{\partial N_8}{\partial y} && 0 \\
0 && 0 && \frac{\partial N_1}{\partial z} && \dots && 0 && 0 && \frac{\partial N_8}{\partial z} \\
0 && \frac{\partial N_1}{\partial z} && \frac{\partial N_1}{\partial y} && \dots && 0 && \frac{\partial N_8}{\partial z} && \frac{\partial N_8}{\partial y} \\
\frac{\partial N_1}{\partial z} && 0 && \frac{\partial N_1}{\partial x} && \dots && \frac{\partial N_8}{\partial z} && 0 && \frac{\partial N_8}{\partial x} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial x} && 0 && \dots && \frac{\partial N_8}{\partial y} && \frac{\partial N_8}{\partial x} && 0
\end{bmatrix}
\\
\begin{bmatrix}
\frac{\partial N_i}{\partial x} \\
\frac{\partial N_i}{\partial y} \\
\frac{\partial N_i}{\partial z}
\end{bmatrix}
=
\boldsymbol{J}^{-1}
\begin{bmatrix}
\frac{\partial N_i}{\partial a} \\
\frac{\partial N_i}{\partial b} \\
\frac{\partial N_i}{\partial c}
\end{bmatrix}
要素剛性マトリクス
要素剛性マトリクスは下記の式で求めることが可能です。
\boldsymbol{K_e} = \int_v \boldsymbol{B}^T \boldsymbol{D}' \boldsymbol{B} dV \\
\boldsymbol{D}' = \boldsymbol{D} : 弾性状態のとき \\
\boldsymbol{D}' = \boldsymbol{D}_{ep} : 塑性状態のとき
変数変換とガウス求積を使用すると下記のように変形できます。
\begin{align}
\boldsymbol{K_e} &= \int \int \int_v \boldsymbol{B}^T\boldsymbol{D}'\boldsymbol{B} dV \\
&= \int_{-1}^1 \int_{-1}^{1} \int_{-1}^{1} \boldsymbol{B}^T\boldsymbol{D}'\boldsymbol{B} \begin{vmatrix} \boldsymbol{J} \end{vmatrix} dadbdc \\
&= \sum_{i=1}^2 \sum_{j=1}^2 \sum_{k=1}^2 w_i w_j w_k \boldsymbol{B}(a_i,b_i,c_i)^T\boldsymbol{D}'\boldsymbol{B}(a_i,b_i,c_i) \begin{vmatrix} \boldsymbol{J}(a_i,b_i,c_i) \end{vmatrix}
\end{align}
\\
w_i : 重み係数 \\
\begin{align}
w_1 = 1 & &&a_1 = b_1 = c_1 = -\sqrt{\frac{1}{3}} \\
w_2 = 1 & &&a_2 = b_2 = c_2 = \sqrt{\frac{1}{3}}
\end{align}
B-bar要素
上記の処理で6面体要素の解析を行うことが可能ですが、計算結果をAbaqusと比較すると微妙に異なった値になります。
実はAbaqusでは6面体要素に体積ロッキングを防ぐためにB-bar法による選択的低減積分が実装されています。
今回はAbaqusに習って同様のB-bar法を実装してみます。
B-bar法は要素内で体積ひずみを一定にするという処理を組み込みます。
これは、これまで使用してきたBマトリクスを下記で定義される$\bar{\boldsymbol{B}}$マトリクスに変更するだけで実装することができます。
\begin{align}
\bar{\boldsymbol{B}} &= \boldsymbol{B} + \bar{\boldsymbol{B}}_v - \boldsymbol{B}_v \\
\bar{\boldsymbol{B}}_v &= \frac{1}{V} \int_v \boldsymbol{B}_v \begin{vmatrix} \boldsymbol{J} \end{vmatrix} dV \\
&= \frac{1}{V} \int^{1}_{-1} \int^{1}_{-1} \int^{1}_{-1} \boldsymbol{B}_v \begin{vmatrix} \boldsymbol{J} \end{vmatrix} dadbdc \\
&= \frac{1}{V} \sum_{i=1}^2 \sum_{j=1}^2 \sum_{k=1}^2 w_i w_j w_k \boldsymbol{B}_v(a_i,b_i,c_i)\begin{vmatrix} \boldsymbol{J}(a_i,b_i,c_i) \end{vmatrix}
\end{align}
\\
\boldsymbol{B}_v = \frac{1}{3}
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && \frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial z} && \dots && \frac{\partial N_8}{\partial x} && \frac{\partial N_8}{\partial y} && \frac{\partial N_8}{\partial z} \\
\frac{\partial N_1}{\partial x} && \frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial z} && \dots && \frac{\partial N_8}{\partial x} && \frac{\partial N_8}{\partial y} && \frac{\partial N_8}{\partial z} \\
\frac{\partial N_1}{\partial x} && \frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial z} && \dots && \frac{\partial N_8}{\partial x} && \frac{\partial N_8}{\partial y} && \frac{\partial N_8}{\partial z} \\
0 && 0 && 0 && \dots && 0 && 0 && 0 \\
0 && 0 && 0 && \dots && 0 && 0 && 0 \\
0 && 0 && 0 && \dots && 0 && 0 && 0 \\
\end{bmatrix}
\\
V : 要素の体積
6面体要素をPythonで実装する
上記の6面体要素の計算を行うクラスをPythonで実装します。
このクラスを実装するためにまずは節点を格納するクラスNodeを実装します。
Node.py
# 3次元節点格納用のクラス
class Node:
# コンストラクタ
# no : 節点番号
# x : x座標
# y : y座標
# z : z座標
def __init__(self, no, x, y, z):
self.no = no # 節点番号
self.x = x # x座標
self.y = y # y座標
self.z = z # z座標
次に6面体要素の計算を行うクラスC3D8を実装します。
makeKetmatrix関数で要素接線剛性マトリクスを計算します。
update関数は要素の節点の変位からリターンマッピング法により、要素内の積分点の応力、各ひずみ、Dマトリクスを計算します。また引数incNoは増分解析で使用されるインクリメントの番号で0から始まる整数値を入力します。
makeqVector関数は現在の要素の応力の状態から要素内の内力ベクトルを計算します。
C3D8.py
import numpy as np
import numpy.linalg as LA
from Dmatrix import Dmatrix
from ElementOutputData import ElementOutputData
# 6面体8節点要素のクラス
class C3D8:
# コンストラクタ
# no : 要素番号
# nodes : 節点の集合(Node型のリスト)
# matSec : # 材料情報(MaterialSet型)
def __init__(self, no, nodes, matSet):
# インスタンス変数を定義する
self.nodeNum = 8 # 節点の数
self.nodeDof = 3 # 節点の自由度
self.no = no # 要素番号
self.nodes = nodes # 節点の集合(Node型のリスト)
self.young = matSet.young # ヤング率
self.poisson = matSet.poisson # ポアソン比
self.density = matSet.density # 密度
self.material = matSet.material # 材料の構成則
self.ipNum = 8 # 積分点の数
self.w1 = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # 積分点の重み係数1
self.w2 = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # 積分点の重み係数2
self.w3 = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0] # 積分点の重み係数3
self.ai = np.array([-np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), -np.sqrt(1.0 / 3.0), # 積分点の座標(a,b,c座標系, np.array型のリスト)
-np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), -np.sqrt(1.0 / 3.0)])
self.bi = np.array([-np.sqrt(1.0 / 3.0), -np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), # 積分点の座標(a,b,c座標系, np.array型のリスト)
-np.sqrt(1.0 / 3.0), -np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0)])
self.ci = np.array([-np.sqrt(1.0 / 3.0), -np.sqrt(1.0 / 3.0), -np.sqrt(1.0 / 3.0), -np.sqrt(1.0 / 3.0), # 積分点の座標(a,b,c座標系, np.array型のリスト)
np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0)])
self.incNo = 0 # インクリメントのNo
# 要素内の変位、応力、塑性ひずみを初期化する
self.vecDisp = np.zeros(self.nodeNum * self.nodeDof) # 要素内の変位
self.yeildFlgList = [] # 要素が降伏しているか判定するフラグ
self.vecEStrainList = [] # 要素内の弾性ひずみ(np.array型のリスト)
self.vecPStrainList = [] # 要素内の塑性ひずみ(np.array型のリスト)
self.ePStrainList = [] # 要素内の相当塑性ひずみ(リスト)
self.vecStressList = [] # 要素内の応力(np.array型のリスト)
self.misesList = [] # 要素内のミーゼス応力(リスト)
for i in range(self.ipNum):
self.yeildFlgList.append(False)
self.vecEStrainList.append(np.zeros(6))
self.vecPStrainList.append(np.zeros(6))
self.ePStrainList.append(0.0)
self.vecStressList.append(np.zeros(6))
self.misesList.append(0.0)
# 前回のインクリメントのひずみを初期化する
self.vecPrevEStrainList = [] # 要素内の弾性ひずみ(np.array型のリスト)
self.vecPrevPStrainList = [] # 要素内の塑性ひずみ(np.array型のリスト)
self.prevEPStrainList = [] # 要素内の相当塑性ひずみ(リスト)
for i in range(self.ipNum):
self.vecPrevEStrainList.append(np.zeros(6))
self.vecPrevPStrainList.append(np.zeros(6))
self.prevEPStrainList.append(0.0)
# Dマトリクスを初期化する
self.matD = []
for i in range(self.ipNum):
self.matD.append(self.makeDematrix())
# 要素接線剛性マトリクスKetを作成する
def makeKetmatrix(self):
# ヤコビ行列を計算する
matJ = []
for i in range(self.ipNum):
matJ.append(self.makeJmatrix(self.ai[i], self.bi[i], self.ci[i]))
# Bbarマトリクスを計算する
matBbar = []
for i in range(self.ipNum):
matBbar.append(self.makeBbarmatrix(self.ai[i], self.bi[i], self.ci[i]))
# Ketマトリクスをガウス積分で計算する
matKet = np.zeros([self.nodeDof * self.nodeNum, self.nodeDof * self.nodeNum])
for i in range(self.ipNum):
matKet += self.w1[i] * self.w2[i] * self.w3[i] * matBbar[i].T @ self.matD[i] @ matBbar[i] * LA.det(matJ[i])
return matKet
# 弾性状態のDマトリクスを作成する
def makeDematrix(self):
matD = Dmatrix(self.young, self.poisson).makeDematrix()
return matD
# ヤコビ行列を計算する
# a : a座標値
# b : b座標値
# c : c座標値
def makeJmatrix(self, a, b, c):
# dNdabを計算する
matdNdabc = self.makedNdabc(a, b, c)
# xi, yi, ziの行列を計算する
matxiyizi = np.array([[self.nodes[0].x, self.nodes[0].y, self.nodes[0].z],
[self.nodes[1].x, self.nodes[1].y, self.nodes[1].z],
[self.nodes[2].x, self.nodes[2].y, self.nodes[2].z],
[self.nodes[3].x, self.nodes[3].y, self.nodes[3].z],
[self.nodes[4].x, self.nodes[4].y, self.nodes[4].z],
[self.nodes[5].x, self.nodes[5].y, self.nodes[5].z],
[self.nodes[6].x, self.nodes[6].y, self.nodes[6].z],
[self.nodes[7].x, self.nodes[7].y, self.nodes[7].z]])
# ヤコビ行列を計算する
matJ = matdNdabc @ matxiyizi
# ヤコビアンが負にならないかチェックする
if LA.det(matJ) < 0:
raise ValueError("要素の計算に失敗しました")
return matJ
# Bマトリクスを作成する
# a : a座標値
# b : b座標値
# c : c座標値
def makeBmatrix(self, a, b, c):
# dNdabcの行列を計算する
matdNdabc = self.makedNdabc(a, b, c)
# ヤコビ行列を計算する
matJ = self.makeJmatrix(a, b, c)
# matdNdxyz = matJinv * matdNdabc
matdNdxyz = LA.solve(matJ, matdNdabc)
# Bマトリクスを計算する
matB = np.empty((6,0))
for i in range(self.nodeNum):
matTmp = np.array([[matdNdxyz[0, i], 0.0, 0.0],
[0.0, matdNdxyz[1, i], 0.0],
[0.0, 0.0, matdNdxyz[2, i]],
[0.0, matdNdxyz[2, i], matdNdxyz[1, i]],
[matdNdxyz[2, i], 0.0, matdNdxyz[0, i]],
[matdNdxyz[1, i], matdNdxyz[0, i], 0.0]])
matB = np.hstack((matB, matTmp))
return matB
# Bbarマトリクスを作成する
# a : a座標値
# b : b座標値
# c : c座標値
def makeBbarmatrix(self, a, b, c):
# Bマトリクスを作成する
matB = self.makeBmatrix(a, b, c)
# Bvマトリクスを作成する
matBv = self.makeBvmatrix(a, b, c)
# Bvbarマトリクスを作成する
matBvbar = self.makeBvbarmatrix()
# Bbarマトリクスを計算する
matBbar = matBvbar + matB - matBv
return matBbar
# Bvマトリクスを作成する
# a : a座標値
# b : b座標値
# c : c座標値
def makeBvmatrix(self, a, b, c):
# dNdabcの行列を計算する
matdNdabc = self.makedNdabc(a, b, c)
# ヤコビ行列を計算する
matJ = self.makeJmatrix(a, b, c)
# matdNdxyz = matJinv * matdNdabc
matdNdxyz = LA.solve(matJ, matdNdabc)
# Bvマトリクスを計算する
matBv = np.empty((6,0))
for i in range(self.nodeNum):
matTmp = np.array([[matdNdxyz[0, i], matdNdxyz[1, i], matdNdxyz[2, i]],
[matdNdxyz[0, i], matdNdxyz[1, i], matdNdxyz[2, i]],
[matdNdxyz[0, i], matdNdxyz[1, i], matdNdxyz[2, i]],
[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0]])
matBv = np.hstack((matBv, matTmp))
matBv *= 1.0 / 3.0
return matBv
# Bvbarマトリクスを作成する
def makeBvbarmatrix(self):
# 体積を計算する
v = self.getVolume()
# Bvマトリクスを計算する
matBv = []
for i in range(self.ipNum):
matBv.append(self.makeBvmatrix(self.ai[i], self.bi[i], self.ci[i]))
# ヤコビ行列を計算する
matJ = []
for i in range(self.ipNum):
matJ.append(self.makeJmatrix(self.ai[i], self.bi[i], self.ci[i]))
# ガウス積分でBvbarマトリクスを計算する
Bvbar = np.zeros([6, self.nodeNum * self.nodeDof])
for i in range(self.ipNum):
Bvbar += self.w1[i] * self.w2[i] * self.w3[i] * matBv[i] * LA.det(matJ[i])
Bvbar *= 1.0 / v
return Bvbar
# dNdabcの行列を計算する
# a : a座標値
# b : b座標値
# c : c座標値
def makedNdabc(self, a, b, c):
# dNi/da, dNi/db, dNi/dcを計算する
dN1da = -0.125 * (1.0 - b) * (1.0 - c)
dN2da = 0.125 * (1.0 - b) * (1.0 - c)
dN3da = 0.125 * (1.0 + b) * (1.0 - c)
dN4da = -0.125 * (1.0 + b) * (1.0 - c)
dN5da = -0.125 * (1.0 - b) * (1.0 + c)
dN6da = 0.125 * (1.0 - b) * (1.0 + c)
dN7da = 0.125 * (1.0 + b) * (1.0 + c)
dN8da = -0.125 * (1.0 + b) * (1.0 + c)
dN1db = -0.125 * (1.0 - a) * (1.0 - c)
dN2db = -0.125 * (1.0 + a) * (1.0 - c)
dN3db = 0.125 * (1.0 + a) * (1.0 - c)
dN4db = 0.125 * (1.0 - a) * (1.0 - c)
dN5db = -0.125 * (1.0 - a) * (1.0 + c)
dN6db = -0.125 * (1.0 + a) * (1.0 + c)
dN7db = 0.125 * (1.0 + a) * (1.0 + c)
dN8db = 0.125 * (1.0 - a) * (1.0 + c)
dN1dc = -0.125 * (1.0 - a) * (1.0 - b)
dN2dc = -0.125 * (1.0 + a) * (1.0 - b)
dN3dc = -0.125 * (1.0 + a) * (1.0 + b)
dN4dc = -0.125 * (1.0 - a) * (1.0 + b)
dN5dc = 0.125 * (1.0 - a) * (1.0 - b)
dN6dc = 0.125 * (1.0 + a) * (1.0 - b)
dN7dc = 0.125 * (1.0 + a) * (1.0 + b)
dN8dc = 0.125 * (1.0 - a) * (1.0 + b)
# dNdabcを計算する
dNdabc = np.array([[dN1da, dN2da, dN3da, dN4da, dN5da, dN6da, dN7da, dN8da],
[dN1db, dN2db, dN3db, dN4db, dN5db, dN6db, dN7db, dN8db],
[dN1dc, dN2dc, dN3dc, dN4dc, dN5dc, dN6dc, dN7dc, dN8dc]])
return dNdabc
# 体積を求める
def getVolume(self):
# ヤコビ行列を計算する
matJ = []
for i in range(self.ipNum):
matJ.append(self.makeJmatrix(self.ai[i], self.bi[i], self.ci[i]))
# ガウス積分で体積を計算する
volume = 0
for i in range(self.ipNum):
volume += self.w1[i] * self.w2[i] * self.w3[i] * LA.det(matJ[i])
return volume
# 要素内の変数を更新する
# vecDisp : 要素節点の変位ベクトル(np.array型)
# incNo : インクリメントNo
def update(self, vecDisp, incNo):
self.returnMapping(vecDisp, incNo)
self.vecDisp = vecDisp
self.incNo = incNo
# Return Mapping法により、応力、塑性ひずみ、降伏判定を更新する
# vecDisp : 要素節点の変位ベクトル(np.array型)
# incNo : インクリメントNo
def returnMapping(self, vecDisp, incNo):
# 各積分点の全ひずみを求める
vecStrainList = self.makeStrainVector(vecDisp)
# リターンマッピング法により、応力、塑性ひずみ、降伏判定を求める
for i in range(self.ipNum):
# リターンマッピング法を計算する
if self.incNo == incNo: # 前回と同じインクリメントの場合
vecStress, vecEStrain, vecPStrain, ePStrain, yieldFlg, matDep = \
self.material.returnMapping3D(vecStrainList[i],
self.vecPrevPStrainList[i],
self.prevEPStrainList[i])
else: # 前回と異なるインクリメントの場合
self.vecPrevEStrainList = self.vecEStrainList
self.vecPrevPStrainList = self.vecPStrainList
self.prevEPStrainList = self.ePStrainList
vecStress, vecEStrain, vecPStrain, ePStrain, yieldFlg, matDep = \
self.material.returnMapping3D(vecStrainList[i],
self.vecPStrainList[i],
self.ePStrainList[i])
self.vecStressList[i] = vecStress
self.vecEStrainList[i] = vecEStrain
self.vecPStrainList[i] = vecPStrain
self.ePStrainList[i] = ePStrain
self.yeildFlgList[i] = yieldFlg
self.misesList[i] = self.misesStress(vecStress)
self.matD[i] = matDep
# 内力ベクトルqを作成する
def makeqVector(self):
# ヤコビ行列を計算する
matJ = []
for i in range(self.ipNum):
matJ.append(self.makeJmatrix(self.ai[i], self.bi[i], self.ci[i]))
# Bbarマトリクスを計算する
matBbar = []
for i in range(self.ipNum):
matBbar.append(self.makeBbarmatrix(self.ai[i], self.bi[i], self.ci[i]))
# 内力ベクトルqを計算する
vecq = np.zeros(self.nodeDof * self.nodeNum)
for i in range(self.ipNum):
vecq += self.w1[i] * self.w2[i] * self.w3[i] * matBbar[i].T @ self.vecStressList[i] * LA.det(matJ[i])
return vecq
# 積分点のひずみベクトルのリストを作成する
# vecDisp : 要素節点の変位のリスト
def makeStrainVector(self, vecDisp):
# Bbarマトリクスを計算する
matBbar = []
for i in range(self.ipNum):
matBbar.append(self.makeBbarmatrix(self.ai[i], self.bi[i], self.ci[i]))
# 積分点のひずみを計算する
vecIpStrains = []
for i in range(self.ipNum):
vecIpStrains.append(np.array(matBbar[i] @ vecDisp))
return vecIpStrains
# ミーゼス応力を計算する
# vecStress : 応力ベクトル(np.array型)
def misesStress(self, vecStress):
tmp1 = np.square(vecStress[0] - vecStress[1]) + np.square(vecStress[1] - vecStress[2]) + np.square(vecStress[2] - vecStress[0])
tmp2 = 6.0 * (np.square(vecStress[3]) + np.square(vecStress[4]) + np.square(vecStress[5]))
mises = np.sqrt(0.5 * (tmp1 + tmp2))
return mises
# 要素の出力データを作成する
def makeOutputData(self):
output = ElementOutputData(self,
self.vecStressList,
self.vecEStrainList,
self.vecPStrainList,
self.ePStrainList,
self.misesList)
return output
最後にmakeOutputData関数は要素の出力データを返す関数です。
解析結果を出力する際に使用します。
要素の出力データはElementOutputDataクラスの形式で返します。
ElementOutputDataは下記のように実装しています。
ElementOutputData.py
# 要素の出力データを格納するクラス
class ElementOutputData:
# コンストラクタ
# element : 要素のクラス
# vecElemDisp : 要素節点の変位のリスト
# vecStressList : 積分点の応力のリスト(np.array型のリスト)
# vecEStrainList : 積分点の弾性ひずみのリスト(np.array型のリスト)
# vecPStrainList : 積分点の塑性ひずみのリスト(np.array型のリスト)
# ePStrainList : 相当塑性ひずみのリスト
# misesList : ミーゼス応力のリスト
def __init__(self, element, vecStressList, vecEStrainList, vecPStrainList, ePStrainList, misesList):
# インスタンス変数を定義する
self.element = element
# 積分点の応力、ひずみを計算する
self.vecIpPStrainList = vecPStrainList # 積分点の塑性ひずみ
self.vecIpStrainList = [] # 積分点のひずみベクトルのリスト(np.arrayのリスト型)
for i in range(len(vecEStrainList)):
vecIpStrain = vecEStrainList[i] + vecPStrainList[i]
self.vecIpStrainList.append(vecIpStrain)
self.ipEPStrainList = ePStrainList # 積分点の相当塑性ひずみ
self.vecIpStressList = vecStressList # 積分点の応力ベクトルのリスト(np.arrayのリスト型)
self.ipMiseses = misesList # 積分点のミーゼス応力
解析を行う処理をPythonで実装する
上記で実装したクラスを使って解析を行うための処理をPythonで実装します。
そのために境界条件を格納するためのクラスBoundaryを実装します。
addSPC関数で節点の拘束を追加し、makeDispVector関数で追加した拘束の変位を表すベクトルを返します。
荷重も同様でaddForce関数で節点の荷重を追加し、makeForceVector関数で荷重ベクトルを返します。
Boundary.py
import numpy as np
# 境界条件を格納するクラス
class Boundary:
# コンストラクタ
# nodeNum : 節点数
def __init__(self, nodeNum):
# インスタンス変数を定義する
self.nodeNum = nodeNum # 全節点数
self.nodeDof = 3 # 節点の自由度
self.vecDisp = np.array(nodeNum * self.nodeDof * [None]) # 単点拘束の強制変位
self.vecForce = np.array(nodeNum * self.nodeDof * [0.0]) # 荷重ベクトル
# 単点拘束を追加する
# nodeNo : 節点番号
# dispX : x方向の強制変位
# dispY : y方向の強制変位
# dispZ : z方向の強制変位
def addSPC(self, nodeNo, dispX, dispY, dispZ):
self.vecDisp[self.nodeDof * (nodeNo - 1) + 0] = dispX
self.vecDisp[self.nodeDof * (nodeNo - 1) + 1] = dispY
self.vecDisp[self.nodeDof * (nodeNo - 1) + 2] = dispZ
# 単点拘束条件から変位ベクトルを作成する
def makeDispVector(self):
return self.vecDisp
# 荷重を追加する
def addForce(self, nodeNo, fx, fy, fz):
self.vecForce[self.nodeDof * (nodeNo - 1) + 0] = fx
self.vecForce[self.nodeDof * (nodeNo - 1) + 1] = fy
self.vecForce[self.nodeDof * (nodeNo - 1) + 2] = fz
# 境界条件から荷重ベクトルを作成する
def makeForceVector(self):
return self.vecForce
次に陰解法の解析を行うFEMクラスを実装します。
コンストラクタで解析を行う全節点と全要素、境界条件とインクリメント数を指定します。
荷重はインクリメントによって等分割され、それぞれニュートン法により計算されます。
impAnalysis関数で解析を行います。解析の結果はoutputTxt関数でテキスト形式で出力することが可能です。
また、接線剛性マトリクスの計算及び境界条件の処理の詳細に関しては有限要素法の弾塑性解析をPythonで実装する(1次元トラス要素)を参照ください。
FEM.py
import numpy as np
import numpy.linalg as LA
class FEM:
# コンストラクタ
# nodes : 節点は1から始まる順番で並んでいる前提(Node型のリスト)
# elements : 要素は種類ごとにソートされている前提(C3D8型のリスト)
# bound : 境界条件(d2Boundary型)
# incNum : インクリメント数
def __init__(self, nodes, elements, bound, incNum):
# インスタンス変数を定義する
self.nodeDof = 3 # 節点の自由度
self.nodes = nodes # 節点は1から始まる順番で並んでいる前提(Node2d型のリスト)
self.elements = elements # 要素は種類ごとにソートされている前提(リスト)
self.bound = bound # 境界条件(d2Boundary型)
self.incNum = incNum # インクリメント数
self.itrNum = 100 # ニュートン法のイテレータの上限
self.rn = 0.005 # ニュートン法の残差力の収束判定のパラメータ
self.cn = 0.01 # ニュートン法の変位の収束判定のパラメータ
# 陰解法で解析を行う
def impAnalysis(self):
self.vecDispList = [] # インクリメント毎の変位ベクトルのリスト(np.array型のリスト)
self.vecRFList = [] # インクリメント毎の反力ベクトルのリスト(np.array型のリスト)
self.elemOutputDataList = [] # インクリメント毎の要素出力のリスト(makeOutputData型のリストのリスト)
# 荷重をインクリメント毎に分割する
vecfList = []
for i in range(self.incNum):
vecfList.append(self.makeForceVector() * (i + 1) / self.incNum)
# ニュートン法により変位を求める
vecDisp = np.zeros(len(self.nodes) * self.nodeDof) # 全節点の変位ベクトル
vecR = np.zeros(len(self.nodes) * self.nodeDof) # 残差力ベクトル
for i in range(self.incNum):
vecDispFirst = vecDisp.copy() # 初期の全節点の変位ベクトル
vecf = vecfList[i] # i+1番インクリメントの荷重
vecBoundDisp = self.bound.makeDispVector()
# 境界条件を考慮しないインクリメント初期の残差力ベクトルRを作成する
if i == 0:
vecR = vecfList[0]
else:
vecR = vecfList[i] - vecfList[i - 1]
# 収束演算を行う
for j in range(self.itrNum):
# 接線剛性マトリクスKtを作成する
matKt = self.makeKtmatrix()
# 境界条件を考慮したKtcマトリクス、Rcベクトルを作成する
matKtc, vecRc = self.setBoundCondition(matKt, vecR, vecBoundDisp, vecDisp)
# Ktcの逆行列が計算できるかチェックする
if np.isclose(LA.det(matKtc), 0.0) :
raise ValueError("有限要素法の計算に失敗しました。")
# 変位ベクトルを計算する
vecd = LA.solve(matKtc, vecRc)
vecDisp += vecd
# 全ての要素内の変数を更新する
self.updateElements(vecDisp, i)
# 新たな残差力ベクトルRを求める
vecQ = np.zeros(len(self.nodes) * self.nodeDof)
for elem in self.elements:
vecq = elem.makeqVector()
for k in range(len(elem.nodes)):
for l in range(elem.nodeDof):
vecQ[(elem.nodes[k].no - 1) * self.nodeDof + l] += vecq[k * elem.nodeDof + l]
vecR = vecf - vecQ
# 新たな境界条件を考慮したRcベクトルを作成する
matKt = self.makeKtmatrix()
matKtc, vecRc = self.setBoundCondition(matKt, vecR, vecBoundDisp, vecDisp)
# 時間平均力を計算する
aveForce = 0.0
cnt = len(self.nodes) * self.nodeDof
for k in range(len(vecQ)):
aveForce += np.abs(vecQ[k])
for k in range(len(vecf)):
if not vecf[k] == 0.0:
aveForce += np.abs(vecf[k])
cnt+= 1
aveForce = aveForce / cnt
# 収束判定を行う
if np.allclose(vecRc, 0.0):
break
if np.isclose(LA.norm(vecd), 0.0):
break
dispRate = LA.norm(vecd) / LA.norm(vecDisp - vecDispFirst)
ResiForceRate = np.abs(vecRc).max() / aveForce
if dispRate < self.cn and ResiForceRate < self.rn:
break
# インクリメントの最終的な変位べクトルを格納する
self.vecDispList.append(vecDisp.copy())
# 変位ベクトルから要素の出力データを計算する
elemOutputDatas = []
for elem in self.elements:
elemOutputData = elem.makeOutputData()
elemOutputDatas.append(elemOutputData)
self.elemOutputDataList.append(elemOutputDatas)
# 節点反力を計算する
vecRF = np.array(vecQ - vecf).flatten()
# インクリメントの最終的な節点反力を格納する
self.vecRFList.append(vecRF)
# 接線剛性マトリクスKtを作成する
def makeKtmatrix(self):
matKt = np.matrix(np.zeros((len(self.nodes) * self.nodeDof, len(self.nodes) * self.nodeDof)))
for elem in self.elements:
# ketマトリクスを計算する
matKet = elem.makeKetmatrix()
# Ktマトリクスに代入する
for c in range(len(elem.nodes) * self.nodeDof):
ct = (elem.nodes[c // self.nodeDof].no - 1) * self.nodeDof + c % self.nodeDof
for r in range(len(elem.nodes) * self.nodeDof):
rt = (elem.nodes[r // self.nodeDof].no - 1) * self.nodeDof + r % self.nodeDof
matKt[ct, rt] += matKet[c, r]
return matKt
# 節点に負荷する荷重、等価節点力を考慮した荷重ベクトルを作成する
def makeForceVector(self):
# 節点に負荷する荷重ベクトルを作成する
vecCondiForce = self.bound.makeForceVector()
vecf = vecCondiForce
return vecf
# Kマトリクス、荷重ベクトルに境界条件を考慮する
# matKt : 接線剛性マトリクス
# vecR : 残差力ベクトル
# vecBoundDisp : 節点の境界条件の変位ベクトル
# vecDisp : 全節点の変位ベクトル(np.array型)
def setBoundCondition(self, matKt, vecR, vecBoundDisp, vecDisp):
matKtc = np.copy(matKt)
vecRc = np.copy(vecR)
# 単点拘束条件を考慮したKマトリクス、荷重ベクトルを作成する
for i in range(len(vecBoundDisp)):
if not vecBoundDisp[i] == None:
# Kマトリクスからi列を抽出する
vecx = np.array(matKt[:, i]).flatten()
# 変位ベクトルi列の影響を荷重ベクトルに適用する
vecRc = vecRc - (vecBoundDisp[i] - vecDisp[i]) * vecx
# Kマトリクスのi行、i列を全て0にし、i行i列の値を1にする
matKtc[:, i] = 0.0
matKtc[i, :] = 0.0
matKtc[i, i] = 1.0
for i in range(len(vecBoundDisp)):
if not vecBoundDisp[i] == None:
vecRc[i] = vecBoundDisp[i] - vecDisp[i]
return matKtc, vecRc
# 全ての要素内の変数を更新する
# vecDisp : 全節点の変位ベクトル(np.array型)
# incNo : インクリメントの番号
def updateElements(self, vecDisp, incNo):
for elem in self.elements:
vecElemDisp = np.zeros(len(elem.nodes) * self.nodeDof)
for i in range(len(elem.nodes)):
for j in range(elem.nodeDof):
vecElemDisp[i * elem.nodeDof + j] = vecDisp[(elem.nodes[i].no - 1) * self.nodeDof + j]
elem.update(vecElemDisp, incNo)
# 解析結果をテキストファイルに出力する
def outputTxt(self, filePath):
# ファイルを作成し、開く
f = open(filePath + ".txt", 'w')
# 出力する文字の情報を定義する
columNum = 20
floatDigits = ".10g"
# 入力データのタイトルを書きこむ
f.write("*********************************\n")
f.write("* Input Data *\n")
f.write("*********************************\n")
f.write("\n")
# 節点情報を出力する
f.write("***** Node Data ******\n")
f.write("No".rjust(columNum) + "X".rjust(columNum) + "Y".rjust(columNum) + "Z".rjust(columNum) + "\n")
f.write("-" * columNum * 4 + "\n")
for node in self.nodes:
strNo = str(node.no).rjust(columNum)
strX = str(format(node.x, floatDigits).rjust(columNum))
strY = str(format(node.y, floatDigits).rjust(columNum))
strZ = str(format(node.z, floatDigits).rjust(columNum))
f.write(strNo + strX + strY + strZ + "\n")
f.write("\n")
# 要素情報を出力する
nodeNoColumNum = 36
f.write("***** Element Data ******\n")
f.write("No".rjust(columNum) + "Type".rjust(columNum) + "Node No".rjust(nodeNoColumNum) +
"Young".rjust(columNum) + "Poisson".rjust(columNum) + "Thickness".rjust(columNum) +
"Area".rjust(columNum) + "Density".rjust(columNum) + "\n")
f.write("-" * columNum * 7 + "-" * nodeNoColumNum + "\n")
for elem in self.elements:
strNo = str(elem.no).rjust(columNum)
strType = str(elem.__class__.__name__ ).rjust(columNum)
strNodeNo = ""
for node in elem.nodes:
strNodeNo += " " + str(node.no)
strNodeNo = strNodeNo.rjust(nodeNoColumNum)
strYoung = str(format(elem.young, floatDigits).rjust(columNum))
strPoisson = "None".rjust(columNum)
if hasattr(elem, 'poisson'):
strPoisson = str(format(elem.poisson, floatDigits).rjust(columNum))
strThickness = "None".rjust(columNum)
if hasattr(elem, 'thickness'):
strThickness = str(format(elem.thickness, floatDigits).rjust(columNum))
strArea = "None".rjust(columNum)
if hasattr(elem, 'area'):
strArea = str(format(elem.area, floatDigits).rjust(columNum))
strDensity = "None".rjust(columNum)
if not elem.density is None:
strDensity = str(format(elem.density, floatDigits).rjust(columNum))
f.write(strNo + strType + strNodeNo + strYoung + strPoisson +
strThickness + strArea + strDensity + "\n")
f.write("\n")
# 単点拘束情報を出力する
f.write("***** SPC Constraint Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Displacement".rjust(columNum) + "Y Displacement".rjust(columNum) +
"Z Displacement".rjust(columNum) + "\n")
f.write("-" * columNum * 4 + "\n")
vecBoundDisp = self.bound.makeDispVector()
for i in range(self.bound.nodeNum):
strFlg = False
for j in range(self.bound.nodeDof):
if not vecBoundDisp[i * self.bound.nodeDof + j] is None:
strFlg = True
if strFlg == True:
strNo = str(i + 1).rjust(columNum)
strXDisp = "None".rjust(columNum)
if not vecBoundDisp[i * self.bound.nodeDof] is None:
strXDisp = str(format(vecBoundDisp[i * self.bound.nodeDof], floatDigits).rjust(columNum))
strYDisp = "None".rjust(columNum)
if not vecBoundDisp[i * self.bound.nodeDof + 1] is None:
strYDisp = str(format(vecBoundDisp[i * self.bound.nodeDof + 1], floatDigits).rjust(columNum))
strZDisp = "None".rjust(columNum)
if not vecBoundDisp[i * self.bound.nodeDof + 2] is None:
strZDisp = str(format(vecBoundDisp[i * self.bound.nodeDof + 2], floatDigits).rjust(columNum))
f.write(strNo + strXDisp + strYDisp + strZDisp + "\n")
f.write("\n")
# 荷重条件を出力する(等価節点力も含む)
f.write("***** Nodal Force Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Force".rjust(columNum) + "Y Force".rjust(columNum) +
"Z Force".rjust(columNum) + "\n")
f.write("-" * columNum * 4 + "\n")
vecf = self.makeForceVector()
for i in range(len(self.nodes)):
strFlg = False
for j in range(self.bound.nodeDof):
if not vecf[i * self.bound.nodeDof + j] == 0.0:
strFlg = True
if strFlg == True:
strNo = str(i + 1).rjust(columNum)
strXForce = str(format(vecf[i * self.bound.nodeDof], floatDigits).rjust(columNum))
strYForce = str(format(vecf[i * self.bound.nodeDof + 1], floatDigits).rjust(columNum))
strZForce = str(format(vecf[i * self.bound.nodeDof + 2], floatDigits).rjust(columNum))
f.write(strNo + strXForce + strYForce + strZForce + "\n")
f.write("\n")
# 結果データのタイトルを書きこむ
f.write("**********************************\n")
f.write("* Result Data *\n")
f.write("**********************************\n")
f.write("\n")
for i in range(self.incNum):
f.write("*Increment " + str(i + 1) + "\n")
f.write("\n")
# 変位のデータを出力する
f.write("***** Displacement Data ******\n")
f.write("NodeNo".rjust(columNum) + "Magnitude".rjust(columNum) + "X Displacement".rjust(columNum) +
"Y Displacement".rjust(columNum) + "Z Displacement".rjust(columNum) + "\n")
f.write("-" * columNum * 5 + "\n")
for j in range(len(self.nodes)):
strNo = str(j + 1).rjust(columNum)
vecDisp = self.vecDispList[i]
mag = np.linalg.norm(np.array((vecDisp[self.nodeDof * j], vecDisp[self.nodeDof * j + 1], vecDisp[self.nodeDof * j + 2])))
strMag = str(format(mag, floatDigits).rjust(columNum))
strXDisp = str(format(vecDisp[self.nodeDof * j], floatDigits).rjust(columNum))
strYDisp = str(format(vecDisp[self.nodeDof * j + 1], floatDigits).rjust(columNum))
strZDisp = str(format(vecDisp[self.nodeDof * j + 2], floatDigits).rjust(columNum))
f.write(strNo + strMag + strXDisp + strYDisp + strZDisp + "\n")
f.write("\n")
# 応力データを出力する
f.write("***** Stress Data ******\n")
f.write("Element No".rjust(columNum) + "Integral No".rjust(columNum) + "Stress XX".rjust(columNum) + "Stress YY".rjust(columNum) +
"Stress ZZ".rjust(columNum) + "Stress XY".rjust(columNum) + "Stress XZ".rjust(columNum) + "Stress YZ".rjust(columNum) +
"Mises".rjust(columNum) + "\n")
f.write("-" * columNum * 9 + "\n")
for elemOutputData in self.elemOutputDataList[i]:
elem = elemOutputData.element
strElemNo = str(elem.no).rjust(columNum)
for j in range(elem.ipNum):
strIntNo = str(j + 1).rjust(columNum)
strStressXX = str(format(elemOutputData.vecIpStressList[j][0], floatDigits).rjust(columNum))
strStressYY = str(format(elemOutputData.vecIpStressList[j][1], floatDigits).rjust(columNum))
strStressZZ = str(format(elemOutputData.vecIpStressList[j][2], floatDigits).rjust(columNum))
strStressXY = str(format(elemOutputData.vecIpStressList[j][5], floatDigits).rjust(columNum))
strStressXZ = str(format(elemOutputData.vecIpStressList[j][4], floatDigits).rjust(columNum))
strStressYZ = str(format(elemOutputData.vecIpStressList[j][3], floatDigits).rjust(columNum))
strMises = str(format(elemOutputData.ipMiseses[j], floatDigits).rjust(columNum))
f.write(strElemNo + strIntNo + strStressXX + strStressYY + strStressZZ +
strStressXY + strStressXZ + strStressYZ + strMises + "\n")
f.write("\n")
# 全ひずみデータを出力する
f.write("***** Strain Data ******\n")
f.write("Element No".rjust(columNum) + "Integral No".rjust(columNum) + "Strain XX".rjust(columNum) + "Strain YY".rjust(columNum) +
"Strain ZZ".rjust(columNum) + "Strain XY".rjust(columNum) + "Strain XZ".rjust(columNum) + "Strain YZ".rjust(columNum) + "\n")
f.write("-" * columNum * 8 + "\n")
for elemOutputData in self.elemOutputDataList[i]:
elem = elemOutputData.element
strElemNo = str(elem.no).rjust(columNum)
for j in range(elem.ipNum):
strIntNo = str(j + 1).rjust(columNum)
strStrainXX = str(format(elemOutputData.vecIpStrainList[j][0], floatDigits).rjust(columNum))
strStrainYY = str(format(elemOutputData.vecIpStrainList[j][1], floatDigits).rjust(columNum))
strStrainZZ = str(format(elemOutputData.vecIpStrainList[j][2], floatDigits).rjust(columNum))
strStrainXY = str(format(elemOutputData.vecIpStrainList[j][5], floatDigits).rjust(columNum))
strStrainXZ = str(format(elemOutputData.vecIpStrainList[j][4], floatDigits).rjust(columNum))
strStrainYZ = str(format(elemOutputData.vecIpStrainList[j][3], floatDigits).rjust(columNum))
f.write(strElemNo + strIntNo + strStrainXX + strStrainYY + strStrainZZ +
strStrainXY + strStrainXZ + strStrainYZ +"\n")
f.write("\n")
# 塑性ひずみデータを出力する
f.write("***** Plastic Strain Data ******\n")
f.write("Element No".rjust(columNum) + "Integral No".rjust(columNum) + "PStrain XX".rjust(columNum) + "PStrain YY".rjust(columNum) +
"PStrain ZZ".rjust(columNum) + "PStrain XY".rjust(columNum) + "PStrain XZ".rjust(columNum) + "PStrain YZ".rjust(columNum) +
"Equivalent Plastic Strain".rjust(30) + "\n")
f.write("-" * (columNum * 8 + 30) + "\n")
for elemOutputData in self.elemOutputDataList[i]:
elem = elemOutputData.element
strElemNo = str(elem.no).rjust(columNum)
for j in range(elem.ipNum):
strIntNo = str(j + 1).rjust(columNum)
strPStrainXX = str(format(elemOutputData.vecIpPStrainList[j][0], floatDigits).rjust(columNum))
strPStrainYY = str(format(elemOutputData.vecIpPStrainList[j][1], floatDigits).rjust(columNum))
strPStrainZZ = str(format(elemOutputData.vecIpPStrainList[j][2], floatDigits).rjust(columNum))
strPStrainXY = str(format(elemOutputData.vecIpPStrainList[j][5], floatDigits).rjust(columNum))
strPStrainXZ = str(format(elemOutputData.vecIpPStrainList[j][4], floatDigits).rjust(columNum))
strPStrainYZ = str(format(elemOutputData.vecIpPStrainList[j][3], floatDigits).rjust(columNum))
strEPStrain = str(format(elemOutputData.ipEPStrainList[j], floatDigits).rjust(30))
f.write(strElemNo + strIntNo + strPStrainXX + strPStrainYY + strPStrainZZ +
strPStrainXY + strPStrainXZ + strPStrainYZ + strEPStrain + "\n")
f.write("\n")
# 反力のデータを出力する
f.write("***** Reaction Force Data ******\n")
f.write("NodeNo".rjust(columNum) + "Magnitude".rjust(columNum) + "X Force".rjust(columNum) + "Y Force".rjust(columNum) +
"Z Force".rjust(columNum) + "\n")
f.write("-" * columNum * 5 + "\n")
for j in range(len(self.nodes)):
strNo = str(j + 1).rjust(columNum)
vecRF = self.vecRFList[i]
mag = np.linalg.norm(np.array((vecRF[self.nodeDof * j], vecRF[self.nodeDof * j + 1], vecRF[self.nodeDof * j + 2])))
strMag = str(format(mag, floatDigits).rjust(columNum))
strXForce = str(format(vecRF[self.nodeDof * j], floatDigits).rjust(columNum))
strYForce = str(format(vecRF[self.nodeDof * j + 1], floatDigits).rjust(columNum))
strZForce = str(format(vecRF[self.nodeDof * j + 2], floatDigits).rjust(columNum))
f.write(strNo + strMag + strXForce + strYForce + strZForce + "\n")
f.write("\n")
# ファイルを閉じる
f.close()
サンプルを解く
解析モデル
上記で実装したクラスを使って下記の簡単なサンプルを解いてみます。
曲げ変形が支配的になるので、本来であればもっと細かく要素分割する必要がありますが、今回は計算が正しいか確認するだけなので、このモデルで解析を行ってみます。
サンプルを解く処理を実装する
上記のサンプルを解く処理を実装します。
main.py
from Node import Node
from MaterialSet import MaterialSet
from MisesMaterial import MisesMaterial
from Boundary import Boundary
from FEM import FEM
from C3D8 import C3D8
# メインの処理
def main():
# 節点リストを定義する
node1 = Node(1, 0.0, 0.0, 0.0)
node2 = Node(2, 1.0, 0.0, 0.0)
node3 = Node(3, 2.0, 0.0, 0.0)
node4 = Node(4, 3.0, 0.0, 0.0)
node5 = Node(5, 0.0, 0.0, 1.0)
node6 = Node(6, 1.0, 0.0, 1.0)
node7 = Node(7, 2.0, 0.0, 1.0)
node8 = Node(8, 3.0, 0.0, 1.0)
node9 = Node(9, 0.0, 1.0, 0.0)
node10 = Node(10, 1.0, 1.0, 0.0)
node11 = Node(11, 2.0, 1.0, 0.0)
node12 = Node(12, 3.0, 1.0, 0.0)
node13 = Node(13, 0.0, 1.0, 1.0)
node14 = Node(14, 1.0, 1.0, 1.0)
node15 = Node(15, 2.0, 1.0, 1.0)
node16 = Node(16, 3.0, 1.0, 1.0)
nodes = [node1, node2, node3, node4, node5, node6, node7, node8,
node9, node10, node11, node12, node13, node14, node15, node16]
nodes1 = [node1, node2, node10, node9, node5, node6, node14, node13]
nodes2 = [node2, node3, node11, node10, node6, node7, node15, node14]
nodes3 = [node3, node4, node12, node11, node7, node8, node16, node15]
# 材料特性を定義する
young = 210000.0
poisson = 0.3
mat = MisesMaterial(young, poisson)
mat.addStressPStrainLine(400000, 0.0)
mat.addStressPStrainLine(500000, 0.5)
mat.addStressPStrainLine(600000, 0.7)
mat.addStressPStrainLine(700000, 1.0)
matSet = MaterialSet("None", young, poisson, material=mat)
# 要素リストを定義する
elem1 = C3D8(1, nodes1, matSet)
elem2 = C3D8(2, nodes2, matSet)
elem3 = C3D8(3, nodes3, matSet)
elems = [elem1, elem2, elem3]
# 境界条件を定義する
bound = Boundary(len(nodes))
bound.addSPC(1, 0.0, 0.0, 0.0)
bound.addSPC(5, 0.0, 0.0, 0.0)
bound.addSPC(9, 0.0, 0.0, 0.0)
bound.addSPC(13, 0.0, 0.0, 0.0)
bound.addForce(4, 0.0, 0.0, -10000.0)
bound.addForce(8, 0.0, 0.0, -10000.0)
bound.addForce(12, 0.0, 0.0, -10000.0)
bound.addForce(16, 0.0, 0.0, -10000.0)
# 解析を実行する
fem = FEM(nodes, elems, bound, 1)
fem.impAnalysis()
# 結果を出力する
fem.outputTxt("test")
if __name__ == '__main__':
main()
解析結果はtest.txtに出力されます。
Abaqus Student Edition2021と計算結果を比較する
上記の計算結果が正しいか確認するためにAbaqusを使用して確かめてみます。
Abaqusで同様のサンプルの入力ファイルを作成し、結果を確認してみます。
Abqusの入力ファイル
*node
1, 0.0, 0.0, 0.0
2, 1.0, 0.0, 0.0
3, 2.0, 0.0, 0.0
4, 3.0, 0.0, 0.0
5, 0.0, 0.0, 1.0
6, 1.0, 0.0, 1.0
7, 2.0, 0.0, 1.0
8, 3.0, 0.0, 1.0
9, 0.0, 1.0, 0.0
10, 1.0, 1.0, 0.0
11, 2.0, 1.0, 0.0
12, 3.0, 1.0, 0.0
13, 0.0, 1.0, 1.0
14, 1.0, 1.0, 1.0
15, 2.0, 1.0, 1.0
16, 3.0, 1.0, 1.0
*element, type=C3D8, elset=elems
1, 1, 2, 10, 9, 5, 6, 14, 13
2, 2, 3, 11, 10, 6, 7, 15, 14
3, 3, 4, 12, 11, 7, 8, 16, 15
*material, name=mat
*elastic
210000, 0.3
*plastic
400000, 0.0
500000, 0.5
600000, 0.7
700000, 1.0
*solid section, material=mat, elset=elems
*boundary
1, 1, 3
5, 1, 3
9, 1, 3
13, 1, 3
*step
*static, direct
1.0, 1.0
*cload
4, 3, -10000,0
8, 3, -10000,0
12, 3, -10000,0
16, 3, -10000,0
*matrix generate, stiffness
*element matrix output, elset=elems, stiffness=yes, outputfile=user
*end step
各節点の変位量を比較してみます。
Abaqusとは収束条件が違うため、完全一致はしませんが、有効数字3桁まで一致します。
参考文献
The Equivalence of the Radial Return and Mendelson Methods for Integrating the Classical Plasticity Equations
計算破壊力学のための応用有限要素法プログラム実装



