概要
有限要素法の弾塑性解析をPythonで実装してみます。
ただ、最初から多次元の弾塑性を考えるのは難しいので、まずは1次元で実装してみます。
本来は大変形解析になるので、有限ひずみ理論を使う必要がありますが、今回は簡単のため微小ひずみ理論に基づいた陰解法で実装します。
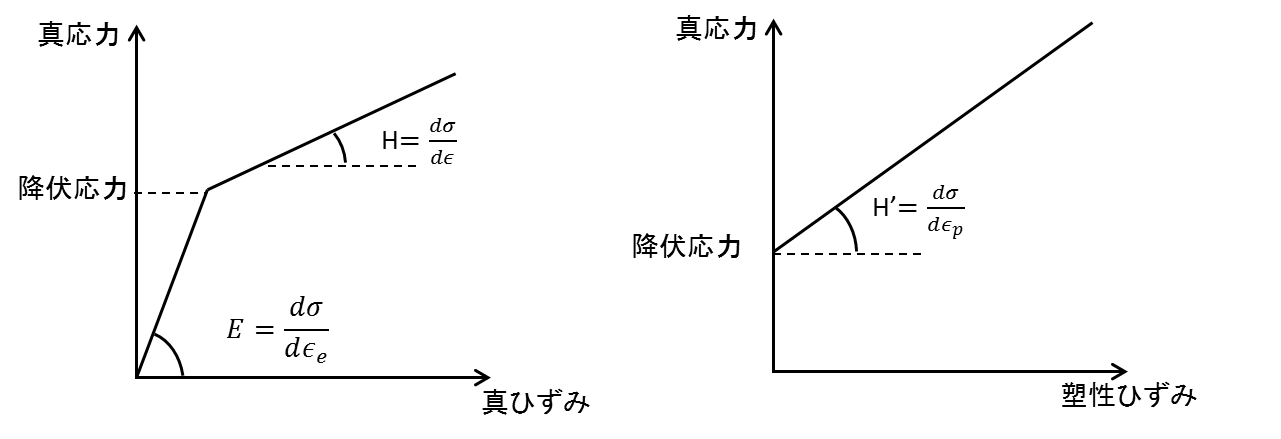
また、材料の特性は下記のように線形硬化で表せる前提です。

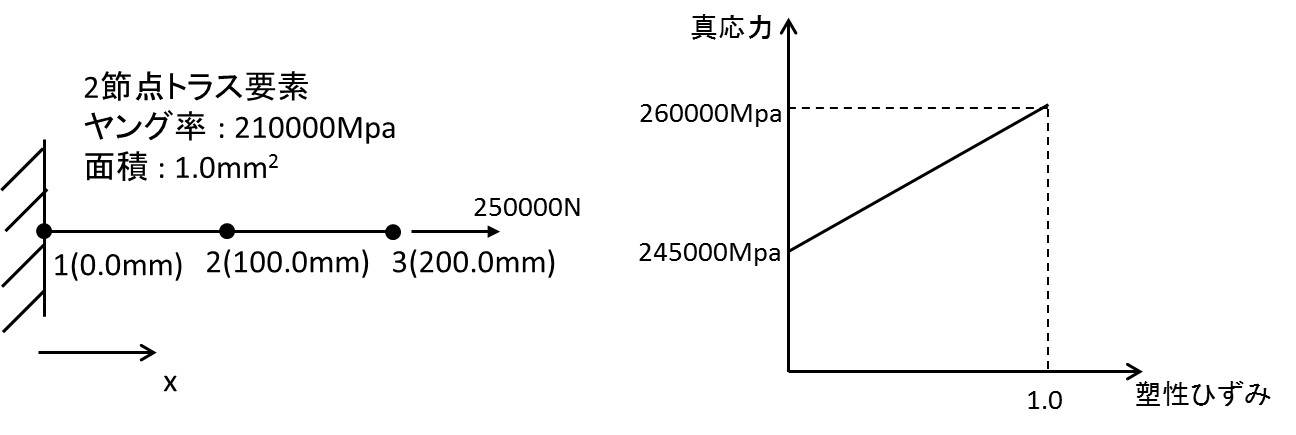
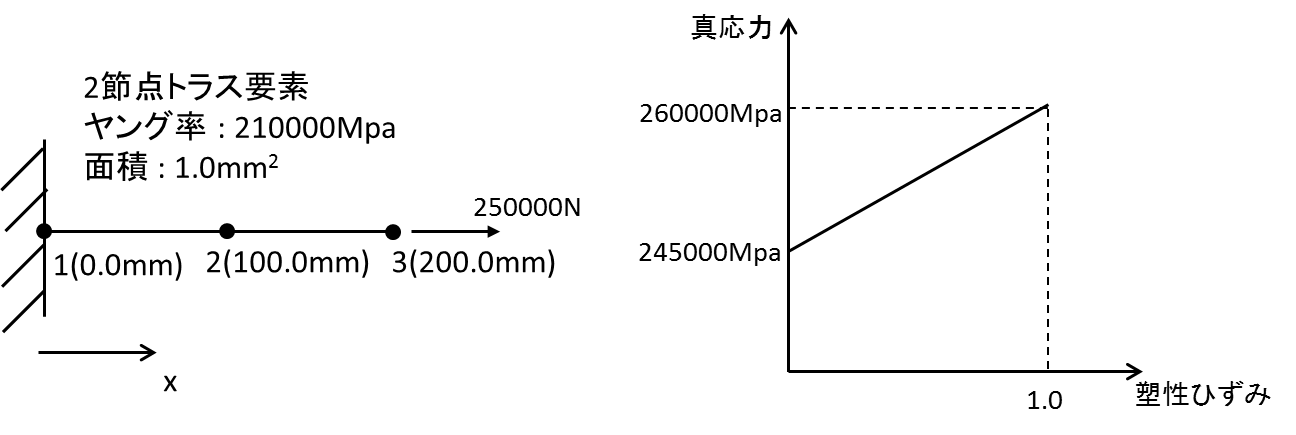
また、この記事では下記の例題を解いてみます。
履歴
続編として非線形硬化に対応した材料の弾塑性解析の記事を作成しました。
有限要素法の弾塑性解析をPythonで実装する(1次元トラス要素、非線形硬化)
弾塑性解析の処理の流れ
弾塑性解析では、増分解法を用いた解析が行われます。
増分解法では荷重もしくは強制変位を幾つかに分割し、段階的に荷重を負荷させて、変位、ひずみ、応力などを求める手法です。Abaqusではこの分割をインクリメントと呼んでいるので、本稿でもインクリメントと呼ぶことにします。
荷重をインクリメント毎に分割した後、仮想仕事の原理から導かれる力のつり合い式を使って節点の変位を求めることになりますが、弾塑性では材料が非線形なため、力のつり合い式が非線形になります。
そこで、力のつり合い式を解くためにニュートン・ラプソン法による収束演算を行います。
この収束演算の内の一回の計算のことをAbaqusでは、イテレーションと呼んでいます。
このイテレーションで変位が計算された後に、次のイテレーションで変位を計算するために必要な値をリターンマッピング法によって求めます。
このイテレーションとインクリメントを繰り返すことによって最終的な変位、ひずみ、応力を求めることができます。

弾塑性の応力とひずみの関係
まずは、弾塑性状態の式を導出してみます。
弾塑性では、応力とひずみの関係は下記の図のようになります。
ここで、弾塑性での全ひずみ$\epsilon$は弾性ひずみ$\epsilon_e$と塑性ひずみ$\epsilon_p$を使った下記の式で表されます。
\epsilon = \epsilon_e + \epsilon_p
ここで、ひずみ増分理論により、増分形式を使った下記の式が与えられています。
\left\{
\begin{array}{ll}
d\sigma = E d\epsilon_e \\
d\sigma = H' d\epsilon_p \\
d\sigma = H d\epsilon \\
d\epsilon = d\epsilon_e + d\epsilon_p \\
\end{array}
\right.
\\
\begin{align}
& E &: ヤング率 \\
& H' &: 塑性係数 \\
& H &: 接線係数
\end{align}
ここで、塑性係数$H'$は応力-塑性ひずみ曲線における傾きを表す値で、接線係数$H$は応力-全ひずみ曲線における傾きを表す値です。式を変形すると、$H$は$E$、$H'$から求めることが可能です。
d\epsilon_e = \frac{1}{E} d\sigma \\
d\epsilon_p = \frac{1}{H'} d\sigma \\
d\epsilon = \frac{1}{H} d\sigma \\
\frac{1}{H} d\sigma = \frac{1}{E} d\sigma + \frac{1}{H'} d\sigma \\
\frac{1}{H} = \frac{1}{E} + \frac{1}{H'} \\
H = \frac{EH'}{E + H'}
上記の式から、応力とひずみは下記の式で表せます。
d\sigma = E d\epsilon \quad (弾性のとき)\\
d\sigma = H d\epsilon \quad (塑性のとき)\\
仮想仕事の原理(弾塑性)
次に、仮想仕事の原理を使って弾塑性の力のつり合い式を求めます。
要素内の仮想仕事の原理の式は下記のようになります。
\int_v \delta \boldsymbol{\epsilon}^T \boldsymbol{\sigma} dV =
\int_v \delta \boldsymbol{u}^T \boldsymbol{b} dV + \int_s \delta \boldsymbol{u}^T \boldsymbol{t} dS
\\
\delta \boldsymbol{\epsilon} : 仮想ひずみ \\
\delta \boldsymbol{u} : 仮想変位 \\
\boldsymbol{b} : 物体力 \\
\boldsymbol{t} : 表面力 \\
仮想仕事の原理の導出については下記を参照ください
・仮想仕事の原理
・有限要素法解析Part 1:仮想仕事の原理 - YouTube
ここで、要素内の変位とひずみは節点の変位$\tilde{\boldsymbol{u}}$で下記のように表すことができるという特徴があります。
\boldsymbol{u} = \boldsymbol{N} \tilde{\boldsymbol{u}} \\
\boldsymbol{\epsilon} = \boldsymbol{B} \tilde{\boldsymbol{u}} \\
\begin{align}
&\tilde{\boldsymbol{u}} : 要素節点の変位をまとめたベクトル \\
&\boldsymbol{N} : 形状関数のマトリクス \\
&\boldsymbol{B} : Bマトリクス
\end{align}
上記の導出についてはこちらの記事を参照ください。上記の式を代入すると下記のように表せます。
\delta \tilde{\boldsymbol{u}}^T \int_v \boldsymbol{B}^T \boldsymbol{\sigma} dV = \delta \tilde{\boldsymbol{u}}^T \int_v \boldsymbol{N}^T \boldsymbol{b} dV + \delta \tilde{\boldsymbol{u}}^T \int_s \boldsymbol{N}^T \boldsymbol{t} dS \\
\int_v \boldsymbol{B}^T \boldsymbol{\sigma} dV = \int_v \boldsymbol{N}^T \boldsymbol{b} dV + \int_s \boldsymbol{N}^T \boldsymbol{t} dS \\
ここで、下記のように式を置き換えます。
\boldsymbol{q_e}(\tilde{\boldsymbol{u}}) = \int_v \boldsymbol{B}^T \sigma (\tilde{\boldsymbol{u}}) dV \\
\boldsymbol{f_e} = \int_v \boldsymbol{N}^T \boldsymbol{b} dV + \int_s \boldsymbol{N}^T \boldsymbol{t} dS \\
\boldsymbol{q_e}(\tilde{\boldsymbol{u}}) = \boldsymbol{f_e} \\
\boldsymbol{q_e} : 要素内力ベクトル \\
\boldsymbol{f_e} : 要素の等価節点力
要素内力ベクトル$\boldsymbol{q_e}$内の応力$\boldsymbol{\sigma}$は弾塑性と応力の関係の式より、変位(ひずみ)に依存して式が変わるので、要素内力ベクトル$\boldsymbol{q_e}$は変位(ひずみ)に依存しているとみなすことができます。
上記の式は1つの要素内の式なので、全要素の$\boldsymbol{q_e}$、$\boldsymbol{f_e}$全てまとめて下記のように表すことができます。
\boldsymbol{Q}(\tilde{\boldsymbol{U}}) = \boldsymbol{f} \\
\boldsymbol{Q}(\tilde{\boldsymbol{U}}) = \sum_e \boldsymbol{q_e}(\tilde{\boldsymbol{u}}) \\
\boldsymbol{f} = \sum_e \boldsymbol{f_e} \\
\boldsymbol{Q}(\tilde{\boldsymbol{U}}) : 内力ベクトル \\
\tilde{\boldsymbol{U}} : 全節点の変位をまとめたベクトル \\
\boldsymbol{f} : 等価節点力
ニュートン・ラプソン法
ニュートン・ラプソン法はある関数$f(\boldsymbol{x}) = \boldsymbol{0}$となる$\boldsymbol{x}$を収束演算により求めます。今回の場合は下記の式を解くことが目的となるので、
\boldsymbol{Q}(\tilde{\boldsymbol{U}}) = \boldsymbol{f}
$\boldsymbol{R}$を下記のように定義します。
\boldsymbol{R}(\tilde{\boldsymbol{U}}) = \boldsymbol{Q}(\tilde{\boldsymbol{U}}) - \boldsymbol{f}
$\boldsymbol{R}$は残差力ベクトルと呼ばれます。
この残差力ベクトル$\boldsymbol{R}(\tilde{\boldsymbol{U}})=\boldsymbol{0}$となる$\tilde{\boldsymbol{U}}$が$\boldsymbol{Q}(\tilde{\boldsymbol{U}}) = \boldsymbol{f}$の式を満たすわけです。
ここで、イテレーション$i$番目の$\tilde{\boldsymbol{U}}_i$が既知で、より$\boldsymbol{R}(\tilde{\boldsymbol{U}})=\boldsymbol{0}$になる$\tilde{\boldsymbol{U}}_{i+1}$を求めることを考えてみます。$\tilde{\boldsymbol{U}}_{i+1}$は下記の式で表すことができます。
\tilde{\boldsymbol{U}}_{i+1} = \tilde{\boldsymbol{U}}_{i} + \Delta \tilde{\boldsymbol{U}}
ここで、$\boldsymbol{R}(\tilde{\boldsymbol{U}}_{i+1})$をテイラー展開して、1次の式で近似してみます。
\boldsymbol{R}(\tilde{\boldsymbol{U}}_{i+1}) = \boldsymbol{R}(\tilde{\boldsymbol{U}}_{i} + \Delta \tilde{\boldsymbol{U}})
\approx
\boldsymbol{R}(\tilde{\boldsymbol{U}}_{i}) + \frac{\partial \boldsymbol{R}}{\partial \tilde{\boldsymbol{U}}}(\tilde{\boldsymbol{U}}_{i}) \Delta \tilde{\boldsymbol{U}} = \boldsymbol{0}
すると、下記のように式変形して$\Delta \tilde{\boldsymbol{U}}$を求めることができます。
\frac{\partial \boldsymbol{R}}{\partial \tilde{\boldsymbol{U}}}(\tilde{\boldsymbol{U}}_{i}) \Delta \tilde{\boldsymbol{U}} = - \boldsymbol{R}(\tilde{\boldsymbol{U}}_{i}) \\
\frac{\partial \boldsymbol{Q}}{\partial \tilde{\boldsymbol{U}}}(\tilde{\boldsymbol{U}}_{i}) \Delta \tilde{\boldsymbol{U}} = - \boldsymbol{R}(\tilde{\boldsymbol{U}}_{i}) \\
\Delta \tilde{\boldsymbol{U}} = - (\frac{\partial \boldsymbol{Q}}{\partial \tilde{\boldsymbol{U}}}(\tilde{\boldsymbol{U}}_{i}) )^{-1} \boldsymbol{R}(\tilde{\boldsymbol{U}}_{i}) \\
\Delta \tilde{\boldsymbol{U}} = - \boldsymbol{K_t}^{-1}(\tilde{\boldsymbol{U}}_{i}) \boldsymbol{R}(\tilde{\boldsymbol{U}}_{i}) \\
\boldsymbol{K_t}(\tilde{\boldsymbol{U}}_{i}) = \frac{\partial \boldsymbol{Q}}{\partial \tilde{\boldsymbol{U}}}(\tilde{\boldsymbol{U}}_{i}) \\
\quad \\
\boldsymbol{K_t} : 接線剛性マトリクス
ここで、$\boldsymbol{K_t}$は接線剛性マトリクスと呼ばれ、全要素の要素接線剛性マトリクス$\boldsymbol{K_{et}}$を足し合わせることで求めることができます。
\boldsymbol{K_t}(\tilde{\boldsymbol{U}}_{i}) = \sum_e \boldsymbol{K_{et}}(\tilde{\boldsymbol{u}}_{i}) \\
\boldsymbol{K_{et}}(\tilde{\boldsymbol{u}}_{i}) = \frac{\partial \boldsymbol{q_e}}{\partial \tilde{\boldsymbol{u}}}(\tilde{\boldsymbol{u}}_{i})
また、要素接線剛性マトリクス$\boldsymbol{K_{et}}$は下記の式で求めることができます。
\begin{align}
\boldsymbol{K_{et}} &= \frac{\partial }{\partial \tilde{\boldsymbol{u}}}
\int_v \boldsymbol{B}^T \sigma dV \\
&= \frac{\partial }{\partial \tilde{\boldsymbol{u}}}
\int_v \boldsymbol{B}^T D\epsilon dV \\
&= \frac{\partial }{\partial \tilde{\boldsymbol{u}}}
\int_v \boldsymbol{B}^T D \boldsymbol{B} \tilde{\boldsymbol{u}} dV \\
&= \int_v \boldsymbol{B}^T D \boldsymbol{B} dV
\end{align}
\\
D = E \quad (弾性のとき) \\
D = H \quad (塑性のとき)
上記の式より、要素が弾性状態か塑性状態かによって$\boldsymbol{K_{et}}$の式が変わることが分かります。
弾性か塑性かは前回のイテレーションで求まった変位により、要素が降伏しているかどうかで求めることができます。
上記の式より、$i+1$イテレーションの$\tilde{\boldsymbol{U}}_{i+1}$は$\boldsymbol{K_t}(\tilde{\boldsymbol{U}}_{i})$、$\boldsymbol{R}(\tilde{\boldsymbol{U}}_{i})$により、求まることができます。
そして、次のイテレーションでは残差力ベクトル$\boldsymbol{R}(\boldsymbol{U}_{i+1})$が必要となります。
この残差力は内力ベクトル$\boldsymbol{Q}(\tilde{\boldsymbol{U}}_{i+1})$から求めれば良いのですが、$\boldsymbol{Q}(\tilde{\boldsymbol{U}}_{i+1})$の式は下記のように要素の応力の成分が含まれています。
\boldsymbol{Q}(\tilde{\boldsymbol{U}}_{i+1}) = \sum_e \boldsymbol{q_e}(\tilde{\boldsymbol{u}}_{i+1}) \\
\boldsymbol{q_e}(\tilde{\boldsymbol{u}}_{i+1}) = \int_v \boldsymbol{B}^T \sigma (\tilde{\boldsymbol{u}}_{i+1}) dV
ここで、応力は変位の経路に依存して変化するため、変位$\tilde{\boldsymbol{u}}_{i+1}$だけでは応力は求めることができません。
また、変位だけでは塑性ひずみ$\epsilon_p$を求めることができません。
そこで、これらの値を求めるためにリターンマッピング法というアルゴリズムを使います。
リターンマッピング法(1次元)
定式化
リターンマッピング法は塑性変形中は必ず降伏関数が0になるという条件のもと、塑性ひずみ$\epsilon_p$と応力$\sigma$を求めます。
降伏関数は下記のように表されます。
f(\sigma, \epsilon_p) = |\sigma| - (\sigma_y + H'|\epsilon_p|) \\
\sigma_y : 降伏応力
この降伏関数が0より小さければ変形は弾性、0より大きければ変形は塑性になります。
そして、塑性変形中は降伏関数が0になるという特徴があります。
ここで、流れ則という理論によると、塑性ひずみ速度$\dot{\epsilon}_p$は下記のように表されます。
\dot{\epsilon}_p = \dot{\gamma} \frac{\partial f}{\partial \sigma} \\
\dot{\gamma} : 塑性乗数
ここで、$\dot{\epsilon}_p$は下記の式で表すことができます。
\dot{\epsilon}_p = |\dot{\epsilon}_p| sign(\sigma) \\
ここで、$sign$は符号関数になります。
上記の式を使って塑性乗数$\dot{\gamma}$は下記の式で表せます。
\frac{\partial f}{\partial \sigma} = sign(\sigma) \\
|\dot{\epsilon}_p| sign(\sigma) = \dot{\gamma} sign(\sigma) \\
\dot{\gamma} = |\dot{\epsilon}_p|
上の式から塑性乗数$\dot{\gamma}$は塑性ひずみ速度の絶対値$|\dot{\epsilon}_p|$と等価なことがわかります。
次に塑性ひずみ$\epsilon_p$を求めることを考えてみます。ニュートン・ラプソン法により、イテレーション$i$の塑性ひずみ$\epsilon_{p,i}$が求められたとき、次の塑性ひずみ$\epsilon_{p,i+1}$は下記の式で求めることにします。
\epsilon_{p,i+1} = \epsilon_{p,i} + \Delta \epsilon_{p} \\
\Delta \epsilon_{p} = \dot{\epsilon}_{p,i+1} \Delta t \\
\Delta t : イテレーション間の時間
ここで、$\Delta \epsilon_{p}$を求めるために、$\dot{\epsilon}_{p,i+1}$の値を使っているので、後退Euler法と呼ばれます。陰解法では後退Euler法を使いますが、陽解法では逆の前進Euler法を使います。
今回は陰解法なので、後退Euler法です。
ここで、$\Delta \epsilon_{p}$の式をこれまでの式を使って変形すると下記の式で表すことができます。
\begin{align}
\Delta \epsilon_{p} &= \dot{\epsilon}_{p,i+1} \Delta t \\
&= |\dot{\epsilon}_{p,i+1}| sign(\sigma_{i+1}) \Delta t \\
&= \dot{\gamma}_{i+1} sign(\sigma_{i+1}) \Delta t \\
&= \Delta \gamma sign(\sigma_{i+1}) \\
\end{align}
\\
\Delta \gamma = \dot{\gamma}_{i+1} \Delta t
さらに絶対値を付け加えた$|\epsilon_{p,i+1}|$も後退Euler法により下記のように表すことができます。
\begin{align}
|\epsilon_{p,i+1}| &= |\epsilon_{p,i}| + |\dot{\epsilon}_{p,i+1}| \Delta t \\
&= |\epsilon_{p,i}| + |\Delta \epsilon_{p}| \\
&= |\epsilon_{p,i}| + \Delta \gamma
\end{align}
次に、イテレーション$i+1$の応力$\sigma_{i+1}$を考えてみます。イテレーション$i+1$の応力$\sigma_{i+1}$は下記の式で与えられます。
\sigma_{i+1} = E \epsilon_{e,i+1} = E (\epsilon_{i+1} - \epsilon_{p,i+1})
ここで、$\epsilon^{tri}_{i+1}$、$\sigma^{tri}_{i+1}$を下記のように定義してみます。
\epsilon^{tri}_{i+1} = \epsilon_{i+1} - \epsilon_{p,i} \\
\sigma^{tri}_{i+1} = E \epsilon^{tri}_{i+1}
$\epsilon^{tri}_{i+1}$は試行ひずみ、$\sigma^{tri}_{i+1}$は試行応力と呼ばれます。
この式を使うと、応力$\sigma_{i+1}$は下記の式で表すことができます。
\begin{align}
\sigma_{i+1} &= E (\epsilon_{i+1} - \epsilon_{p,i+1}) \\
&= E (\epsilon_{i+1} - \epsilon_{p,i} + \epsilon_{p,i} - \epsilon_{p,i+1}) \\
&= E (\epsilon^{tri}_{i+1} - \Delta \epsilon_{p}) \\
&= \sigma^{tri}_{i+1} - E \Delta \gamma sign(\sigma_{i+1})
\end{align}
次に上の式の各項に符号関数が付くように変形してみます。
\sigma_{i+1} = \sigma^{tri}_{i+1} - E \Delta \gamma sign(\sigma) \\
|\sigma_{i+1}|sign(\sigma_{i+1}) = |\sigma^{tri}_{i+1}|sign(\sigma^{tri}_{i+1}) - E \Delta \gamma sign(\sigma_{i+1}) \\
(|\sigma_{i+1}| + E \Delta \gamma)sign(\sigma_{i+1}) = |\sigma^{tri}_{i+1}|sign(\sigma^{tri}_{i+1})
ここで、$\Delta \gamma$は下記のように定義されるので必ず0以上の値になることが分かります。
\begin{align}
\Delta \gamma &= \dot{\gamma}_{p,i+1} \Delta t \\
&= |\dot{\epsilon}_{p,i+1}| \Delta t
\end{align}
すると先ほどの式は符号関数以外の部分が正となるので、下記のように表すことができます。
(|\sigma_{i+1}| + E \Delta \gamma)sign(\sigma_{i+1}) = |\sigma^{tri}_{i+1}|sign(\sigma^{tri}_{i+1}) \\
|\sigma_{i+1}| + E \Delta \gamma \geq 0 \\
|\sigma^{tri}_{i+1}| \geq 0 \\
sign(\sigma_{i+1}) = sign(\sigma^{tri}_{i+1}) \\
|\sigma_{i+1}| + E \Delta \gamma = |\sigma^{tri}_{i+1}|
ここで、降伏関数に$\sigma^{tri}_{i+1}$、$\epsilon_{p, i}$を代入した$f^{tri}_{i+1}$を以下のように定義します。
f^{tri}_{i+1} = f(\sigma^{tri}_{i+1} ,\epsilon_{p, i}) = |\sigma^{tri}_{i+1}| - (\sigma_y + H'|\epsilon_{p,i}|) \\
この$f^{tri}_{i+1}$は0より小さければ弾性変形、0より大きければ塑性変形と判定することができます。
理由については下記で導出します。ここで、本来の$f(\sigma_{i+1}, \epsilon_{p, i+1})$を使えば弾性、塑性の判断ができるわけですが、$\sigma_{i+1}$は残念ながらまだ分かっていません。
そこで、$f(\sigma_{i+1}, \epsilon_{p, i+1})$の式をこれまでの式を使って変形してみます。
\begin{align}
f(\sigma_{i+1}, \epsilon_{p, i+1}) &= |\sigma_{i+1}| - (\sigma_y + H'|\epsilon_{p,i+1}|) \\
&= |\sigma^{tri}_{i+1}| - E \Delta \gamma - (\sigma_y + H'|\epsilon_{p,i+1}|) \\
&= |\sigma^{tri}_{i+1}| - E \Delta \gamma - \{\sigma_y + H'(|\epsilon_{p,i}| + \Delta \gamma)\} \\
&= |\sigma^{tri}_{i+1}| - (\sigma_y + H'|\epsilon_{p,i}|) - (E + H')\Delta \gamma \\
&= f^{tri}_{i+1} - (E + H')\Delta \gamma
\end{align}
ここで、$\Delta \gamma$は弾性変形のときは$0$になり、塑性変形のときは$0$以上になるので、弾性変形のときは$f(\sigma_{i+1}, \epsilon_{p, i+1}) = f^{tri}_{i+1}$となり、$f^{tri}_{i+1}$と一致します。また、塑性変形の時は$\Delta \gamma$は正で$E$, $H'$も正となるので、$f(\sigma_{i+1}, \epsilon_{p, i+1}) \leq f^{tri}_{i+1}$となります。このため、$f^{tri}_{i+1}$の値を使って、弾性か塑性か判断することが可能となります。
また、塑性変形中は$f(\sigma_{i+1}, \epsilon_{p, i+1}) = 0$となるので、
f^{tri}_{i+1} - (E + H')\Delta \gamma = 0 \\
\Delta \gamma = \frac{f^{tri}_{i+1}}{E + H'}
より、$\Delta \gamma$を求めることができます。すると、塑性ひずみ$\epsilon_{p, i+1}$と応力$\sigma_{i+1}$はこれまでの式を使って下記の式で求めることができます。
\sigma_{i+1} = \sigma^{tri}_{i+1} - E \Delta \gamma sign(\sigma_{i+1}) = \sigma^{tri}_{i+1} - E \Delta \gamma sign(\sigma^{tri}_{i+1}) \\
\epsilon_{p,i+1} = \epsilon_{p,i} + \Delta \epsilon_{p} = \epsilon_{p,i} + \Delta \gamma sign(\sigma_{i+1}) = \epsilon_{p,i} + \Delta \gamma sign(\sigma^{tri}_{i+1})
これでようやくリターンマッピング法の定式化ができたので、アルゴリズムをまとめてみます。
① 試行応力$\sigma_{i+1}^{tri}$を計算する
\sigma^{tri}_{i+1} = E (\epsilon_{i+1} - \epsilon_{p,i})
② $f^{tri}_{i+1}$を計算する
f^{tri}_{i+1} = f(\sigma^{tri}_{i+1} ,\epsilon_{p, i}) = |\sigma^{tri}_{i+1}| - (\sigma_y + H'|\epsilon_{p,i}|) \\
③ $f^{tri}_{i+1} \leq 0$ならば$\Delta \gamma = 0$、$f^{tri}_{i+1} > 0$ならば下記の式で$\Delta \gamma$を計算する
\Delta \gamma = \frac{f^{tri}_{i+1}}{E + H'}
④塑性ひずみ$\epsilon_{p, i+1}$と応力$\sigma_{i+1}$を計算する
\sigma_{i+1} = \sigma^{tri}_{i+1} - E \Delta \gamma sign(\sigma^{tri}_{i+1}) \\
\epsilon_{p,i+1} = \epsilon_{p,i} + \Delta \gamma sign(\sigma^{tri}_{i+1})
Pythonで実装する
この処理をPythonでMaterialクラスとして実装してみます。
ここで、塑性係数$H'$を求めるために弾塑性の材料情報を入力する必要がありますが、Abaqusの仕様にならって、データを下記の図のように入力します。

入力ポイントの追加はaddStressPStrainLine関数で実装しています。
後は、 returnMapping関数で全ひずみとひとつ前のイテレーションで求めた塑性ひずみを入力することで塑性ひずみと応力、降伏判定を返すように作成しています。
このクラスを要素のクラスから呼び出すことで要素の塑性ひずみと応力が計算できるように作成しています。
Material.py
import numpy as np
# 材料情報を格納するクラス
class Material:
# コンストラクタ
# young : ヤング率
# area : 面積
def __init__(self, young, area):
# インスタンス変数を定義する
self.young = young # ヤング率
self.area = area # 面積
self.stressLine = [] # 応力-塑性ひずみ多直線の応力データ
self.pStrainLine = [] # 応力-塑性ひずみ多直線の塑性ひずみデータ
# 応力-塑性ひずみ直線のデータを追加する
# (入力されるデータは塑性ひずみが小さい順になり、最初の塑性ひずみは0.0にならなければいけない)
# (入力データは2個だけになる前提)
# (塑性係数は正になる前提)
# stress : 応力(正の前提)
# pStrain : 塑性ひずみ(正の前提)
def addStressPStrainLine(self, stress, pStrain):
# 入力チェック
if len(self.pStrainLine) == 0:
if not pStrain == 0.0 :
raise ValueError("応力-塑性ひずみ直線データの最初のひずみは0.0になる必要があります。")
elif self.pStrainLine[-1] > pStrain:
raise ValueError("応力-塑性ひずみ直線データの入力順序が間違っています。")
elif len(self.pStrainLine) == 2:
raise ValueError("3個以上のデータは入力できません。")
# 最初の入力の場合は降伏応力を格納する
if len(self.stressLine) == 0:
self.yieldStress = stress # 降伏応力
self.stressLine.append(stress)
self.pStrainLine.append(pStrain)
# 降伏関数を計算する
# (0より大きければ降伏している)
# stress : 応力
# pStrain : 塑性ひずみ
def yieldFunction(self, stress, pStrain):
if hasattr(self, 'yieldStress'):
hDash = self.makePlasticModule(pStrain)
f = np.abs(stress) - (self.yieldStress + hDash * np.abs(pStrain))
else:
return 0.0
return f
# 塑性係数を求める
# pStrain : 塑性ひずみ
def makePlasticModule(self, pStrain):
# pStrainが何番目のデータの間か求める
no = None
for i in range(len(self.pStrainLine) - 1):
if self.pStrainLine[i] <= np.abs(pStrain) and np.abs(pStrain) <= self.pStrainLine[i+1]:
no = i
if no is None :
raise ValueError("塑性ひずみが定義した範囲を超えています。")
# 塑性係数を計算する
h = (self.stressLine[no+1] - self.stressLine[no]) / (self.pStrainLine[no+1] - self.pStrainLine[no])
return h
# Return Mapping法により、ひずみ増分、降伏判定を更新する
# strain : 全ひずみ
# prevPStrain : 前回の塑性ひずみ
def returnMapping(self, strain, prevPStrain):
# 試行弾性応力を求める
triStrain = strain - prevPStrain
triStress = self.young * triStrain
# 降伏関数を計算する
triF = self.yieldFunction(triStress, np.abs(prevPStrain))
# 降伏判定を計算する
if triF > 0.0 :
yeildFlg = True
else:
yeildFlg = False
# 塑性ひずみの増分量を計算する
deltaGamma = 0.0
if triF > 0.0 :
hDash = self.makePlasticModule(prevPStrain)
deltaGamma = triF / (self.young + hDash)
deltaPStrain = deltaGamma * np.sign(triStress)
# 塑性ひずみを計算する
pStrain = prevPStrain + deltaPStrain
# 応力を計算する
stress = triStress - self.young * deltaPStrain
return stress, pStrain, yeildFlg
定式化は少し難しいですが、アルゴリズム自体は結構単純です。
トラス要素(弾塑性)
ここでは、トラス要素の要素接線剛性マトリクス$\boldsymbol{K_{et}}$と要素内力ベクトル$\boldsymbol{q_e}$を求める処理を実装します。
要素内力ベクトル
要素内力ベクトル$\boldsymbol{q_e}$は下記の式で表すことができました。
\boldsymbol{q_e} = \int_v \boldsymbol{B}^T \sigma dV \\
上の式の$\sigma$はリターンマッピング法により求めることが可能です。
ただ、$\boldsymbol{q_e}$はこのままでは積分が入っていて少し求めるのが面倒です。
そこで、要素内力ベクトル$\boldsymbol{q_e}$を正規座標系$a$に変数変換してガウス求積を使って求めます。
\begin{align}
\boldsymbol{q_e} &= \int_v \boldsymbol{B}^T \sigma dV \\
&= A \int \boldsymbol{B}^T \sigma dx \\
&= A \int_{-1}^{1} \boldsymbol{B}^T \sigma \frac{dx}{da} da \\
&= A w \boldsymbol{B}^T \sigma \frac{dx}{da}
\end{align}
\\
\boldsymbol{B} =
\begin{bmatrix}
-\frac{1}{-x_1 + x_2} && \frac{1}{-x_1 + x_2} \\
\end{bmatrix}
\\
\frac{d x}{d a} = \frac{1}{2}(-x_1 + x_2)
\\
x_i : i節点のx座標値 \\
A : 断面積 \\
w = 2.0 : 重み係数
$\boldsymbol{B}$マトリクスの導出、正規座標系についてはこちらの記事を参照ください。
要素接線剛性マトリクス
トラス要素の接線剛性マトリクスは上述の通り、下記の式で表されます。
\begin{align}
\boldsymbol{K_{et}} = \int_v \boldsymbol{B}^T D \boldsymbol{B} dv
\end{align}
\\
D = E \quad (弾性のとき) \\
D = H \quad (塑性のとき)
ここで、トラス要素の節点を正規座標系$a$に変数変換してガウス求積を使うと、下記のように求めることができます。
\begin{align}
\boldsymbol{K_{et}} &= \int_v \boldsymbol{B}^T D \boldsymbol{B} dv \\
&= A \int \boldsymbol{B}^TD\boldsymbol{B} dx \\
&= A \int_{-1}^{1} \boldsymbol{B}^TD\boldsymbol{B} \frac{d x}{d a} da \\
&= Aw \boldsymbol{B}^T D\boldsymbol{B} \frac{d x}{d a}
\end{align}
\\
A : 断面積 \\
w = 2.0 : 重み係数
Pythonで実装する
上記の計算を行うトラス要素のクラスd1t2と節点を格納するクラスNode1dを作成してみます。
Node1dクラスは基本的には節点情報を格納するだけです。
d1t2クラスはコンストラクタで先ほど作成したMaterialクラスを引数にとり、要素接線剛性マトリクスの計算などで使用します。
また、インスタンス変数に塑性ひずみと応力の値を持っており、returnMapping関数を呼び出すことで更新します。
makeKetmatrix関数で要素接線剛性マトリクス、makeqVector関数で要素内力ベクトルを計算します。
Noded1.py
class Node1d:
# コンストラクタ
# no : 節点番号
# x : x座標
def __init__(self, no, x):
self.no = no # 節点番号
self.x = x # x座標
# 節点の情報を表示する
def printNode(self):
print("Node No: %d, x: %f" % (self.no, self.x))
d1t2.py
import numpy as np
import numpy.linalg as LA
# 1次元2節点トラス要素のクラス
class d1t2:
# コンストラクタ
# no : 要素番号
# nodes : 節点のリスト(Node1d型のリスト)
# material : 材料特性(Material型)
def __init__(self, no, nodes, material):
# インスタンス変数を定義する
self.no = no # 要素番号
self.nodes = nodes # 節点のリスト(Node1d型のリスト形式)
self.mat = material # 材料データ(Material型)
self.area = material.area # 断面積
self.young = material.young # ヤング率
self.ipNum = 1 # 積分点の数
self.w = 2.0 # 積分点の重み係数
self.yeildFlg = False # 要素が降伏しているか判定するフラグ
self.pStrain = 0.0 # 要素内の塑性ひずみ
self.stress = 0.0 # 要素内の応力
# Bマトリクスを計算する
self.matB = self.makeBmatrix()
# 要素接線剛性マトリクスKetを作成する
def makeKetmatrix(self):
# dxdaを計算する
dxda = -0.5 * self.nodes[0].x + 0.5 * self.nodes[1].x
# 降伏状態を判定し、Dを作成する
if self.yeildFlg == False:
D = self.young
else:
hDash = self.mat.makePlasticModule(self.pStrain)
D = self.young * hDash / (self.young + hDash)
# 要素接線剛性マトリクスKetを計算する
matKet = self.area * self.w * self.matB.T * D * self.matB * dxda
return matKet
# Bマトリクスを作成する
def makeBmatrix(self):
# Bマトリクスを計算する
dN1dx = -1 / (-self.nodes[0].x + self.nodes[1].x)
dN2dx = 1 / (-self.nodes[0].x + self.nodes[1].x)
matB = np.matrix([[dN1dx, dN2dx]])
return matB
# Return Mapping法により、ひずみ増分、降伏判定を更新する
# vecElemDisp : 要素節点の変位ベクトル(np.array型)
def returnMapping(self, vecElemDisp):
# ひずみを求める
strain = np.array(self.matB @ vecElemDisp).flatten()
# リターンマッピング法により、応力、塑性ひずみ、降伏判定を求める
stress, pStrain, yieldFlg = self.mat.returnMapping(strain, self.pStrain)
self.stress = stress
self.pStrain = pStrain
self.yeildFlg = yieldFlg
# 内力ベクトルqを作成する
def makeqVector(self):
# dxdaを計算する
dxda = -0.5 * self.nodes[0].x + 0.5 * self.nodes[1].x
# 内力ベクトルqを計算する
vecq = np.array(self.area * self.w * self.matB.T @ self.stress * dxda).flatten()
return vecq
接線剛性マトリクス
次は接線剛性マトリクスを作成します。
接線剛性マトリクス$\boldsymbol{K_t}$は1次元の場合、全節点数を$N$とすると下記のように表されます。
\boldsymbol{K_t}=
\begin{bmatrix}
K_{11} && K_{12} && \cdots && K_{1, N} \\
K_{21} && K_{22} && \cdots && K_{2, N} \\
\vdots && \vdots && \ddots && \vdots \\
K_{N, 1} && K_{N, 2} && \cdots && K_{N, N}
\end{bmatrix}
上記のように、$N×N$の行列になります。ここで、トラス要素の要素接線剛性マトリクスは節点数2個なので$2×2$の行列になります。そのため、接線剛性マトリクスに足し合わせるために対応する行列の位置を求める必要があります。
トラス要素の節点番号を$i$, $j$とすると、接線剛性マトリクスに格納する位置は下記のように表すことができます。
\boldsymbol{K_{et}}=
\begin{bmatrix}
K_{i, i} && K_{i, j} \\
K_{i, j} && K_{j, j} \\
\end{bmatrix}
境界条件の処理
上記によって、$\boldsymbol{K_t}$が求まり、いよいよ$\Delta \tilde{\boldsymbol{U}}$の計算の準備が整ったわけですが、その前に境界条件を考慮する必要があります。
今回は$\boldsymbol{K_t} \Delta \tilde{\boldsymbol{U}}= \boldsymbol{R}$に単点拘束の境界条件を考慮した処理を行います。
単点拘束とは一つの節点自由度で構成される拘束のことで、例えば$u_1 = 0(u_1: 節点1の変位)$などの拘束を言います。
ここで、例として、接線剛性マトリクスが$3×3$で既知量$u_2 = \bar{u}$の場合で考えます。
すると、下記のように表すことができます。
\begin{bmatrix}
K_{11} && K_{12} && K_{13} \\
K_{21} && K_{22} && K_{23} \\
K_{31} && K_{32} && K_{33} \\
\end{bmatrix}
\begin{bmatrix}
u_1 \\
\bar{u} \\
u_3 \\
\end{bmatrix}
=
\begin{bmatrix}
r_1 \\
r_2 \\
r_3 \\
\end{bmatrix}
\\
K_{11} u_1 + K_{12} \bar{u} + K_{13} u_3 = r_1 \\
K_{21} u_1 + K_{22} \bar{u} + K_{23} u_3 = r_2 \\
K_{31} u_1 + K_{32} \bar{u} + K_{33} u_3 = r_3 \\
既知量を右に移動すると
K_{11} u_1 + K_{13} u_3 = r_1 - K_{12} \bar{u} \\
K_{21} u_1 + K_{23} u_3 = r_2 - K_{22} \bar{u} \\
K_{31} u_1 + K_{33} u_3 = r_3 - K_{32} \bar{u}
となり、真ん中の式を省いて代わりに、$u_2 = \bar{u}$を代入すると、
K_{11} u_1 + K_{13} u_3 = r_1 - K_{12} \bar{u} \\
u_2 = \bar{u} \\
K_{31} u_1 + K_{33} u_3 = r_3 - K_{32} \bar{u} \\
\begin{bmatrix}
K_{11} && 0 && K_{13} \\
0 && 1 && 0 \\
K_{31} && 0 && K_{33}
\end{bmatrix}
\begin{bmatrix}
u_1 \\
\bar{u} \\
u_3
\end{bmatrix}
=
\begin{bmatrix}
r_1 \\
\bar{u} \\
r_3
\end{bmatrix}
-
\begin{bmatrix}
K_{12} \\
0 \\
K_{32}
\end{bmatrix}
\bar{u}
とすることができます。ここで、式を一つ省くことを行っていますが、一般に節点が拘束されている点の荷重値(反力)は未知数なので、未知の値$f_2$を行列から消して変位を求めることが可能となります。
このような処理をすることで、$\boldsymbol{K_t} \Delta \tilde{\boldsymbol{U}}= \boldsymbol{R}$の式を解くことが可能となります。
ここで境界条件を格納するクラスとしてBoundary1dクラスを実装します。(境界条件の処理を行うクラスは後に実装します。)
基本的には境界条件を格納するだけのクラスです。
addSPC関数で単点拘束を追加、addForce関数で荷重を追加します。makeDispVector関数、makeForceVector関数は設定した拘束条件をベクトルの形で返します。
Boundary1d.py
import numpy as np
class Boundary1d:
# コンストラクタ
# nodeNum : 節点数
def __init__(self, nodeNum):
# インスタンス変数を定義する
self.nodeNum = nodeNum # 全節点数
self.dispNodeNo = [] # 単点拘束の節点番号
self.dispX = [] # 単点拘束の強制変位x
self.forceNodeNo = [] # 荷重が作用する節点番号
self.forceX = [] # x方向の荷重
self.matC = np.empty((0, self.nodeNum)) # 多点拘束用のCマトリクス
self.vecd = np.empty(0) # 多点拘束用のdベクトル
# 単点拘束を追加する
# nodeNo : 節点番号
# x : 強制変位量
def addSPC(self, nodeNo, x):
self.dispNodeNo.append(nodeNo)
self.dispX.append(x)
# 単点拘束条件から変位ベクトルを作成する
def makeDispVector(self):
vecd = np.array([None] * self.nodeNum)
for i in range(len(self.dispNodeNo)):
vecd[(self.dispNodeNo[i] - 1)] = self.dispX[i]
return vecd
# 荷重を追加する
# nodeNo : 節点番号
# fx : 荷重値
def addForce(self, nodeNo, fx):
self.forceNodeNo.append(nodeNo)
self.forceX.append(fx)
# 境界条件から荷重ベクトルを作成する
def makeForceVector(self):
vecf = np.array(np.zeros([self.nodeNum]))
for i in range(len(self.forceNodeNo)):
vecf[(self.forceNodeNo[i] - 1)] += self.forceX[i]
return vecf
# 拘束条件を出力する
def printBoundary(self):
print("Node Number: ", self.nodeNum)
print("SPC Constraint Condition")
for i in range(len(self.dispNodeNo)):
print("Node No: " + str(self.dispNodeNo[i]) + ", x: " + str(self.dispX[i]))
print("Force Condition")
for i in range(len(self.forceNodeNo)):
print("Node No: " + str(self.forceNodeNo[i]) + ", x: " + str(self.forceX[i]))
解析を行うクラスをPythonで実装する
解析を行うクラスの実装を行います。
ここで、弾塑性解析を行う全体の処理の内容をまとめてみます。
①. 荷重をインクリメント毎に分割する。(今回は等分割)
②. 変位$\tilde{\boldsymbol{U}}$を初期化する。
\tilde{\boldsymbol{U}} = \boldsymbol{0}
③. $i$インクリメントの残差力$\boldsymbol{R}$を初期化する。
\boldsymbol{R} = \boldsymbol{f}^{i} - \boldsymbol{f}^{i-1} \\
\boldsymbol{f}^i : iインクリメントの荷重
④. 接線剛性マトリクス$\boldsymbol{K_t}$を計算する。
\boldsymbol{K_t} = \sum_e \boldsymbol{K_{te}} \\
⑤. 接線剛性マトリクス$\boldsymbol{K_t}$と残差力$\boldsymbol{R}$に境界条件の処理を行う。
⑥. 変位の増分$\Delta \tilde{\boldsymbol{U}}$を求めて、変位$\tilde{\boldsymbol{U}}$を更新する。
\Delta \tilde{\boldsymbol{U}} = -\boldsymbol{K_t}^{-1} \boldsymbol{R}(\tilde{\boldsymbol{U}}_{i}) \\
\tilde{\boldsymbol{U}}_{j+1} = \tilde{\boldsymbol{U}}_j + \Delta \tilde{\boldsymbol{U}}
⑦. 要素のひずみを計算する。
\epsilon = \boldsymbol{B}\tilde{\boldsymbol{U}}
⑧. リターンマッピング法により、要素の塑性ひずみ$\epsilon_p$、応力$\sigma$を求める。
⑨. 内力ベクトルを計算する。
\boldsymbol{Q}= \sum_e \boldsymbol{q_e} \\
\boldsymbol{q_e} = \int_v \boldsymbol{B}^T \sigma dV
⑩. 残差力$\boldsymbol{R}$を計算する。
\boldsymbol{R} = \boldsymbol{Q} - \boldsymbol{f}^i
⑪. 収束判定を行う。
収束判定を満たしていなければ④に戻る。
⑫. インクリメントが最後の場合は処理を終了する。そうでなければ、$i = i+1$として③に戻る。
上述で実装したクラスを使って解析を行うためのクラスFEM1dを実装します。
コンストラクタで全節点、全要素、境界条件、インクリメント数を引数にとります。
そして、impAnalysis関数で解析を実行し、outputTxt関数で処理の結果をtxt形式で出力できます。
ここで、荷重はインクリメント毎に等分割されるように設定されています。
また、収束判定は求まった変位が初期状態の変位より十分小さいかどうかで判定しています。
FEM1d.py
import numpy as np
import numpy.linalg as LA
class FEM1d:
# コンストラクタ
# nodes : 節点リスト(節点は1から始まる順番で並んでいる前提(Node1d型のリスト))
# elements : 要素のリスト(d1t2型のリスト)
# boundary : 境界条件(d1Boundary型)
# incNum : インクリメント数
def __init__(self, nodes, elements, boundary, incNum):
self.nodes = nodes # 節点は1から始まる順番で並んでいる前提(Node1d型のリスト)
self.elements = elements # 要素のリスト(d1t2型のリスト)
self.bound = boundary # 境界条件(d1Boundary型)
self.incNum = incNum # インクリメント数
self.itrNum = 100 # ニュートン法のイテレータの上限
self.cn = 0.001 # ニュートン法の変位の収束判定のパラメータ
# 陰解法で解析を行う
def impAnalysis(self):
self.vecDispList = [] # インクリメント毎の変位ベクトルのリスト(np.array型のリスト)
self.vecRFList = [] # インクリメント毎の反力ベクトルのリスト(np.array型のリスト)
# 荷重をインクリメント毎に分割する
vecfList = []
for i in range(self.incNum):
vecfList.append(self.makeForceVector() * (i + 1) / self.incNum)
# ニュートン法により変位を求める
vecDisp = np.zeros(len(self.nodes)) # 全節点の変位ベクトル
vecR = np.zeros(len(self.nodes)) # 残差力ベクトル
for i in range(self.incNum):
vecDispFirst = vecDisp # 初期の全節点の変位ベクトル
vecf = vecfList[i] # i+1番インクリメントの荷重
# 境界条件を考慮しないインクリメント初期の残差力ベクトルRを作成する
if i == 0:
vecR = vecfList[0]
else:
vecR = vecfList[i] - vecfList[i - 1]
# 収束演算を行う
for j in range(self.itrNum):
# 接線剛性マトリクスKtを作成する
matKt = self.makeKtmatrix()
# 境界条件を考慮したKtcマトリクス、Rcベクトルを作成する
matKtc, vecRc = self.setBoundCondition(matKt, vecR)
# Ktcの逆行列が計算できるかチェックする
if np.isclose(LA.det(matKtc), 0.0) :
raise ValueError("有限要素法の計算に失敗しました。")
# 変位ベクトルを計算する
vecd = LA.solve(matKtc, vecRc)
vecDisp += vecd
# 要素内の塑性ひずみ、応力を更新する
self.returnMapping(vecDisp)
# 新たな残差力ベクトルRを求める
vecQ = np.zeros(len(self.nodes))
for elem in self.elements:
vecq = elem.makeqVector()
for k in range(len(elem.nodes)):
vecQ[(elem.nodes[k].no - 1)] += vecq[k]
vecR = vecf - vecQ
# 収束判定を行う
if np.isclose(LA.norm(vecd), 0.0):
break
dispRate = (LA.norm(vecd) / LA.norm(vecDisp - vecDispFirst))
if dispRate < self.cn:
break
# インクリメントの最終的な変位べクトルを格納する
self.vecDispList.append(vecDisp.copy())
# 節点反力を計算する
vecRF = np.array(vecQ - vecf).flatten()
# インクリメントの最終的な節点反力を格納する
self.vecRFList.append(vecRF)
# ReturnMapping法により、要素内の塑性ひずみを更新する
# vecDisp : 全節点の変位ベクトル(np.array型)
def returnMapping(self, vecDisp):
# ReturnMapping法により、要素内の塑性ひずみを更新する
for elem in self.elements:
vecElemDisp = np.zeros(len(elem.nodes))
for i in range(len(elem.nodes)):
vecElemDisp[i] = vecDisp[(elem.nodes[i].no - 1)]
elem.returnMapping(vecElemDisp)
# 接線剛性マトリクスKtを作成する
def makeKtmatrix(self):
matKt = np.matrix(np.zeros((len(self.nodes), len(self.nodes))))
for elem in self.elements:
# ketマトリクスを計算する
matKet = elem.makeKetmatrix()
# Ktマトリクスに代入する
for c in range(len(elem.nodes)):
ct = (elem.nodes[c].no - 1)
for r in range(len(elem.nodes)):
rt = (elem.nodes[r].no - 1)
matKt[ct, rt] += matKet[c, r]
return matKt
# 節点に負荷する荷重ベクトルを作成する
def makeForceVector(self):
vecf = self.bound.makeForceVector()
return vecf
# 接線剛性マトリクス、残差力ベクトルに境界条件を考慮する
# matKt : 接線剛性マトリクス
# vecR : 残差力ベクトル
def setBoundCondition(self, matKt, vecR):
matKtc = np.copy(matKt)
vecRc = np.copy(vecR)
# 単点拘束条件を考慮したKマトリクス、荷重ベクトルを作成する
vecDisp = self.bound.makeDispVector()
for i in range(len(vecDisp)):
if not vecDisp[i] == None:
# Ktマトリクスからi列を抽出する
vecx = np.array(matKt[:, i]).flatten()
# 変位ベクトルi列の影響を荷重ベクトルに適用する
vecRc = vecRc - vecDisp[i] * vecx
# Ktマトリクスのi行、i列を全て0にし、i行i列の値を1にする
matKtc[:, i] = 0.0
matKtc[i, :] = 0.0
matKtc[i, i] = 1.0
for i in range(len(vecDisp)):
if not vecDisp[i] == None:
vecRc[i] = vecDisp[i]
return matKtc, vecRc
# 解析結果をテキストファイルに出力する
# filePath : ファイルを出力するパス(.txtは不要)
def outputTxt(self, filePath):
# ファイルを作成し、開く
f = open(filePath + ".txt", 'w')
# 出力する文字の情報を定義する
columNum = 20
floatDigits = ".10g"
# 入力データのタイトルを書きこむ
f.write("*********************************\n")
f.write("* Input Data *\n")
f.write("*********************************\n")
f.write("\n")
# 節点情報を出力する
f.write("***** Node Data ******\n")
f.write("No".rjust(columNum) + "X".rjust(columNum) + "\n")
f.write("-" * columNum * 2 + "\n")
for node in self.nodes:
strNo = str(node.no).rjust(columNum)
strX = str(format(node.x, floatDigits).rjust(columNum))
f.write(strNo + strX + "\n")
f.write("\n")
# 要素情報を出力する
nodeNoColumNum = columNum
f.write("***** Element Data ******\n")
f.write("No".rjust(columNum) + "Type".rjust(columNum) + "Node No".rjust(nodeNoColumNum) +
"Young".rjust(columNum) + "Area".rjust(columNum) + "\n")
f.write("-" * columNum * 4 + "-" * nodeNoColumNum + "\n")
for elem in self.elements:
strNo = str(elem.no).rjust(columNum)
strType = str(elem.__class__.__name__ ).rjust(columNum)
strNodeNo = ""
for node in elem.nodes:
strNodeNo += " " + str(node.no)
strNodeNo = strNodeNo.rjust(nodeNoColumNum)
strYoung = str(format(elem.young, floatDigits).rjust(columNum))
strArea = str(format(elem.area, floatDigits).rjust(columNum))
f.write(strNo + strType + strNodeNo + strYoung + strArea + "\n")
f.write("\n")
# 単点拘束情報を出力する
f.write("***** SPC Constraint Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Displacement".rjust(columNum) + "\n")
f.write("-" * columNum * 2 + "\n")
for i in range(len(self.bound.dispNodeNo)):
strNo = str(self.bound.dispNodeNo[i]).rjust(columNum)
strXDisp = "None".rjust(columNum)
if not self.bound.dispX[i] is None:
strXDisp = str(format(self.bound.dispX[i], floatDigits).rjust(columNum))
f.write(strNo + strXDisp + "\n")
f.write("\n")
# 荷重条件を出力する(等価節点力も含む)
f.write("***** Nodal Force Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Force".rjust(columNum) + "\n")
f.write("-" * columNum * 2 + "\n")
vecf = self.makeForceVector()
for i in range(len(self.nodes)):
if not vecf[i] == 0 :
strNo = str(i + 1).rjust(columNum)
strXForce = str(format(vecf[i], floatDigits).rjust(columNum))
f.write(strNo + strXForce + "\n")
f.write("\n")
# 結果データのタイトルを書きこむ
f.write("**********************************\n")
f.write("* Result Data *\n")
f.write("**********************************\n")
f.write("\n")
for i in range(self.incNum):
f.write("*Increment " + str(i + 1) + "\n")
f.write("\n")
# 変位のデータを出力する
f.write("***** Displacement Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Displacement".rjust(columNum) + "\n")
f.write("-" * columNum * 2 + "\n")
for j in range(len(self.nodes)):
strNo = str(j + 1).rjust(columNum)
vecDisp = self.vecDispList[i]
strXDisp = str(format(vecDisp[j], floatDigits).rjust(columNum))
f.write(strNo + strXDisp + "\n")
f.write("\n")
# 反力のデータを出力する
f.write("***** Reaction Force Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Force".rjust(columNum) + "\n")
f.write("-" * columNum * 2 + "\n")
for j in range(len(self.nodes)):
strNo = str(j + 1).rjust(columNum)
vecRF = self.vecRFList[i]
strXForce = str(format(vecRF[j], floatDigits).rjust(columNum))
f.write(strNo + strXForce + "\n")
f.write("\n")
# ファイルを閉じる
f.close()
例題を解いてみる
ようやく解析を行うクラスの実装ができたので簡単な例題を解いています。
今回は下の図の例題を解いてみます。
2節点のトラス要素2つが繋がっている構造です。
この例題ではトラス要素に250000Mpaの応力が発生するので、塑性変形するはずです。
Pythonのメインの処理
この例題を解くためのmain.pyを実装します。
main.py
from Node1d import Node1d
from Material import Material
from d1t2 import d1t2
from Boundary1d import Boundary1d
from FEM1d import FEM1d
# メインの処理
def main():
# 節点リストを定義する
node1 = Node1d(1, 0.0)
node2 = Node1d(2, 100.0)
node3 = Node1d(3, 200.0)
nodes = [node1, node2, node3]
nodes1 = [node1, node2]
nodes2 = [node2, node3]
# 材料情報を定義する
area = 1.0
young = 210e3
mat = Material(young, area)
mat.addStressPStrainLine(245e3, 0.0)
mat.addStressPStrainLine(260e3, 1.0)
# 要素リストを定義する
elem1 = d1t2(1, nodes1, mat)
elem2 = d1t2(2, nodes2, mat)
elems = [elem1, elem2]
# 境界条件を定義する
bound = Boundary1d(len(nodes))
bound.addSPC(1, 0.0)
bound.addForce(3, 255e3)
# 解析を行う
fem = FEM1d(nodes, elems, bound, 10)
fem.impAnalysis()
fem.outputTxt("output")
main()
Abaqus Student Edition2021と比較する
解析結果が合っているか確認するためにAbaqus Student Edition2021で検証します。
Abaqusの入力ファイルは下記の通りです。
*node
1, 0.0
2, 100.0
3, 200.0
*element, type=t2d2, elset=elems
1, 1, 2
2, 2, 3
*material, name=mat
*elastic
210e3
*plastic
245e3, 0.0
260e3, 1.0
*solid section, elset=elems, material=mat
1.0
*boundary
1, 1, 1
*step
*static, direct
0.1, 1.0
*cload
3, 1, 255e3
*end step
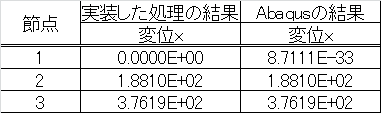
変位の結果を比較してみます。
$10^{-2}$オーダーで一致することが確認できます。
参考文献
Integration Algorithms for Rate-independent Plasticity (1D)
Return Mapping Algorithms and Stress Predictors for Failure Analysis in Geomechanics
U&C 誌上セミナー
有限要素法とは
Solution Methods for Nonlinear
Finite Element Analysis (NFEA)
Solution of the Nonlinear Finite Element Equations in Static AnalysisPart I
On Teaching Finite Element Method in Plasticity With Mathematica
Nonlinear analysis formulation > Elastic-plastic procedures > Tangent (variable)-stiffness method
弾塑性FEMの陰的アルゴリズム① - onigiri_note’s diary
非線形有限要素法のための連続体力学(第2版)