概要
有限要素法で使われる要素の式についてまとめた記事が欲しいなと思ったので作成しました。
有限要素法の各要素をプログラムで実装したい人向けの内容です。
2次元弾性解析限定で要素を実装する際に必要となる式をまとめて記載してみます。
この記事では下記の要素を定式化します。
- 三角形要素
- 三角形2次要素
- 四角形要素
- 四角形2次要素
- トラス要素
- トラス2次要素
また、最初に有限要素法の簡単な定式化を記載します。
有限要素法の定式化(線形弾性)
応力とひずみの関係式
要素内の応力とひずみの関係は下記のように表されます。
\boldsymbol{\sigma} = \boldsymbol{D} \boldsymbol{\epsilon} \\
\boldsymbol{\sigma} =
\begin{bmatrix}
\sigma_x \\
\sigma_y \\
\tau_{xy}
\end{bmatrix}
,
\boldsymbol{\epsilon} =
\begin{bmatrix}
\epsilon_x \\
\epsilon_y \\
\gamma_{xy}
\end{bmatrix}
\\
\quad
\\
\begin{align}
&\sigma_x : x方向の垂直応力 \\
&\sigma_y : y方向の垂直応力 \\
&\tau_{xy} : せん断応力 \\
&\epsilon_x : x方向の垂直ひずみ \\
&\epsilon_y : y方向の垂直ひずみ \\
&\gamma_{xy} : 工学せん断ひずみ \\
&\boldsymbol{D} : 応力-ひずみマトリクス(Dマトリクス)
\end{align}
$\boldsymbol{D}$マトリクスは平面応力状態か平面ひずみ状態かで異なった値となります。
Dマトリクス
平面応力状態
\boldsymbol{D} =
\frac{E}{1-\nu^2}
\begin{bmatrix}
1 && \nu && 0 \\
\nu && 1 && 0 \\
0 && 0 && \frac{1-\nu}{2} \\
\end{bmatrix}
\\
\quad
\\
\begin{align}
&E : ヤング率 \\
&\nu : ポアソン比
\end{align}
平面ひずみ状態
\boldsymbol{D} =
\frac{E}{(1-2\nu)(1+\nu)}
\begin{bmatrix}
1-\nu && \nu && 0 \\
\nu && 1-\nu && 0 \\
0 && 0 && \frac{1-2\nu}{2} \\
\end{bmatrix}
ひずみと変位の関係式
要素内のひずみと変位の関係は下記のように表されます。
\boldsymbol{\epsilon} = \boldsymbol{B} \tilde{\boldsymbol{u}} \\
\boldsymbol{\epsilon} =
\begin{bmatrix}
\epsilon_x \\
\epsilon_y \\
\gamma_{xy}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial u}{\partial x} \\
\frac{\partial v}{\partial y} \\
\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}
\end{bmatrix}
\\
\tilde{\boldsymbol{u}} =
\begin{bmatrix}
u_1 \\
v_1 \\
\vdots \\
u_N \\
v_N
\end{bmatrix}
\\
\quad
\\
\begin{align}
&\boldsymbol{B} : ひずみ-変位マトリクス(Bマトリクス) \\
&u : x方向の変位 \\
&v : y方向の変位 \\
&u_i : i節点のx方向の変位 \\
&v_i : i節点のy方向の変位 \\
&N : 要素の節点数
\end{align}
ここで、$\boldsymbol{B}$マトリクスは要素毎に異なる値になるので、後に要素毎に導出します。
仮想仕事の原理
下の図のように一つの要素に荷重が負荷しているときの仮想仕事の原理を適用してみます。

仮想仕事の原理は仮想的な変位を使って力のつり合い式を表現するために使用されます。
式は下記のように与えられます。
\int_v \delta \boldsymbol{\epsilon}^T \boldsymbol{\sigma} dV =
\int_v \delta \boldsymbol{u}^T \boldsymbol{b} dV + \int_s \delta \boldsymbol{u}^T \boldsymbol{t} dS
\\
\delta \boldsymbol{\epsilon} : 仮想ひずみ \\
\delta \boldsymbol{u} : 仮想変位 \\
\boldsymbol{b} : 物体力 \\
\boldsymbol{t} : 表面力 \\
仮想仕事の原理の導出については下記を参照ください
・仮想仕事の原理
・有限要素法解析Part 1:仮想仕事の原理 - YouTube
ここで、要素内の変位は形状関数$N_i(i = 1 \cdots k)$と節点の変位$\tilde{\boldsymbol{u}}$で表すことができるという特徴があります。
\boldsymbol{u} = \boldsymbol{N} \tilde{\boldsymbol{u}} \\
\boldsymbol{N} =
\begin{bmatrix}
N_1 && 0 && N_2 && 0 && \cdots && N_k && 0 \\
0 && N_1 && 0 && N_2 && \cdots && 0 && N_k \\
\end{bmatrix}
また、要素内の応力は上記の$\boldsymbol{B}$マトリクス、$\boldsymbol{D}$マトリクスを使って下記の式で表すことができます。
\boldsymbol{\sigma} = \boldsymbol{D} \boldsymbol{\epsilon} =
\boldsymbol{D} \boldsymbol{B} \tilde{\boldsymbol{u}} \\
ここで、上記の式を先ほどの仮想仕事の式に代入すると、
\delta \boldsymbol{\epsilon} = \boldsymbol{B} \delta \tilde{\boldsymbol{u}} \\
\delta \boldsymbol{u} = \boldsymbol{N} \delta \tilde{\boldsymbol{u}} \\
\int_v \delta \boldsymbol{\epsilon}^T \boldsymbol{\sigma} dV =
\int_v \delta \boldsymbol{u}^T \boldsymbol{b} dV + \int_s \delta \boldsymbol{u}^T \boldsymbol{t} dS \\
\int_v (\boldsymbol{B} \delta \tilde{\boldsymbol{u}} )^T \boldsymbol{D} \boldsymbol{B} \tilde{\boldsymbol{u}} dV = \int_v (\boldsymbol{N} \delta \tilde{\boldsymbol{u}})^T \boldsymbol{b} dV + \int_s (\boldsymbol{N} \delta \tilde{\boldsymbol{u}})^T \boldsymbol{t} dS \\
\delta \tilde{\boldsymbol{u}} : 要素の節点の仮想変位
となります。ここで、$\delta \tilde{\boldsymbol{u}}$、$\tilde{\boldsymbol{u}}$は節点の変位なので要素内で一定となります。したがって、積分の外に出すことができます。
\delta \tilde{\boldsymbol{u}}^T \int_v \boldsymbol{B}^T \boldsymbol{D} \boldsymbol{B} dV \tilde{\boldsymbol{u}} = \delta \tilde{\boldsymbol{u}}^T \int_v \boldsymbol{N}^T \boldsymbol{b} dV + \delta \tilde{\boldsymbol{u}}^T \int_s \boldsymbol{N}^T \boldsymbol{t} dS \\
$\delta \tilde{\boldsymbol{u}}^T$をはずして式を置き換えます。
\int_v \boldsymbol{B}^T \boldsymbol{D} \boldsymbol{B} dV \tilde{\boldsymbol{u}} = \int_v \boldsymbol{N}^T \boldsymbol{b} dV + \int_s \boldsymbol{N}^T \boldsymbol{t} dS \\
\boldsymbol{K_e} \tilde{\boldsymbol{u}} = \boldsymbol{f_e} \\
\boldsymbol{K_e} = \int_v \boldsymbol{B}^T \boldsymbol{D} \boldsymbol{B} dV \\
\boldsymbol{f_e} = \int_v \boldsymbol{N}^T \boldsymbol{b} dV + \int_s \boldsymbol{N}^T \boldsymbol{t} dS \\
\boldsymbol{K_e} : 要素剛性マトリクス \\
\boldsymbol{f_e} : 等価節点力
ここで、$\boldsymbol{K_e}$は要素剛性マトリクス、$\boldsymbol{f_e}$は等価節点力と呼ばれます。
$\boldsymbol{K_e}$を全体剛性マトリクス$\boldsymbol{K}$に、等価節点力$\boldsymbol{f_e}$を全体荷重ベクトル$\boldsymbol{f}$にまとめることで、全節点の変位$\tilde{\boldsymbol{U}}$を解くことができます。
\boldsymbol{K}\tilde{\boldsymbol{U}} = \boldsymbol{f} \\
\boldsymbol{K} = \sum_e \boldsymbol{K_e} \\
\boldsymbol{f} = \sum_e \boldsymbol{f_e} \\
\tilde{\boldsymbol{U}} : 全節点の変位をまとめたベクトル
有限要素法では$\boldsymbol{K}\tilde{\boldsymbol{U}} = \boldsymbol{f}$を解くことが目的なので、要素毎に$\boldsymbol{K_e}$を求めることが必要となります。$\boldsymbol{K_e}$は要素毎に異なった値となるので、それぞれの要素に対して$\boldsymbol{K_e}$の導出を行います。
要素剛性マトリクス
今回扱う要素は2次元なので要素剛性マトリクス$\boldsymbol{K_e}$は下記の式で表せます。
\boldsymbol{K_e} = \int_V \boldsymbol{B}^T\boldsymbol{D}\boldsymbol{B} dV = t\int \int \boldsymbol{B}^T\boldsymbol{D}\boldsymbol{B} dxdy \\
\\
\quad
\\
\begin{align}
&t : 要素の厚さ
\end{align}
要素剛性マトリクス$\boldsymbol{K_e}$は$\boldsymbol{B}$マトリクス、$\boldsymbol{D}$マトリクスから求めることができますが、xy座標系で求めるのは難しいので、正規化座標系a,bに変数変換して求めます。
正規化座標系では-1から1の範囲の積分になるので、ガウス求積を使うことが可能となります。
そのため、上記は下記のように式変形することができます。
\begin{align}
t\int \int \boldsymbol{B}(x,y)^T\boldsymbol{D}\boldsymbol{B}(x,y) dxdy &=
t\int_{-1}^1 \int_{-1}^1 \boldsymbol{B}(a,b)^T\boldsymbol{D}\boldsymbol{B}(a,b)|\boldsymbol{J}(a,b)| dadb \\
&= t\sum_{i=1}^{N_I} w_i \boldsymbol{B}(a_i,b_i)^T\boldsymbol{D}\boldsymbol{B}(a_i,b_i)|\boldsymbol{J}(a_i,b_i)|
\end{align}
\begin{align}
&\boldsymbol{J} : xy座標系から正規化座標系a,bに変数変換するためのヤコビ行列 \\
&N_I : 積分点の数 \\
&w_i : i番目の積分点の重み係数 \\
&(a_i,b_i) : i番目の積分点の座標
\end{align}
このため、要素の計算は下記の手順で行います。
- $\boldsymbol{D}$マトリクスの計算
- ヤコビ行列$\boldsymbol{J}(a_i,b_i)$の計算
- $\boldsymbol{B}(a_i,b_i)$マトリクスの計算
- 要素剛性マトリクス$\boldsymbol{K_e}$の計算
三角形要素
要素内が定ひずみとなる要素で節点は3個、積分点は1点だけです。
正規化座標系
要素の積分を計算しやすくするために正規化座標系に変換します。

座標変換は形状関数$N_i$を使用した下記の式で与えられます。
\left\{
\begin{array}{ll}
x(a,b) = N_1 x_1 + N_2 x_2 + N_3 x_3 \\
y(a,b) = N_1 y_1 + N_2 y_2 + N_3 y_3 \\
\end{array}
\right.
\\
N_1 = a \\
N_2 = b \\
N_3 = 1 - a - b
要素内の変位は下記の式で与えられます。
\\
\left\{
\begin{array}{ll}
u(a,b) = N_1 u_1 + N_2 u_2 + N_3 u_3 \\
v(a,b) = N_1 v_1 + N_2 v_2 + N_3 v_3 \\
\end{array}
\right.
Bマトリクス
要素内の変位の式から$\boldsymbol{B}$マトリクスは下記の式で与えられます。
\begin{bmatrix}
\epsilon_x \\
\epsilon_y \\
\gamma_{xy}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial u}{\partial x} \\
\frac{\partial v}{\partial y} \\
\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && 0 && \frac{\partial N_2}{\partial x} && 0 && \frac{\partial N_3}{\partial x} && 0 \\
0 && \frac{\partial N_1}{\partial y} && 0 && \frac{\partial N_2}{\partial y} && 0 && \frac{\partial N_3}{\partial y} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial x} &&
\frac{\partial N_2}{\partial y} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_3}{\partial x}
\end{bmatrix}
\begin{bmatrix}
u_1 \\
v_1 \\
u_2 \\
v_2 \\
u_3 \\
v_3
\end{bmatrix}
\\
\boldsymbol{B} =
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && 0 && \frac{\partial N_2}{\partial x} && 0 && \frac{\partial N_3}{\partial x} && 0 \\
0 && \frac{\partial N_1}{\partial y} && 0 && \frac{\partial N_2}{\partial y} && 0 && \frac{\partial N_3}{\partial y} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial x} &&
\frac{\partial N_2}{\partial y} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_3}{\partial x}
\end{bmatrix}
ヤコビ行列
ヤコビ行列$\boldsymbol{J}$は形状関数$N_i$を偏微分した下記の式で与えられます。
\begin{bmatrix}
\frac{\partial N_i}{\partial a} \\
\frac{\partial N_i}{\partial b}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial x}{\partial a} && \frac{\partial y}{\partial a} \\
\frac{\partial x}{\partial b} && \frac{\partial y}{\partial b}
\end{bmatrix}
\begin{bmatrix}
\frac{\partial N_i}{\partial x} \\
\frac{\partial N_i}{\partial y}
\end{bmatrix}
\\
\begin{bmatrix}
\frac{\partial N_i}{\partial a} \\
\frac{\partial N_i}{\partial b}
\end{bmatrix}
=
\boldsymbol{J}
\begin{bmatrix}
\frac{\partial N_i}{\partial x} \\
\frac{\partial N_i}{\partial y}
\end{bmatrix}
\\
\boldsymbol{J}=
\begin{bmatrix}
\frac{\partial x}{\partial a} && \frac{\partial y}{\partial a} \\
\frac{\partial y}{\partial b} && \frac{\partial y}{\partial b}
\end{bmatrix}
=
\begin{bmatrix}
x_1 - x_3 && y_1 - y_3 \\
x_2 - x_3 && y_2 - y_3
\end{bmatrix}
形状関数の偏微分
形状関数$N_i$の$x$,$y$に関する偏微分はヤコビ行列$\boldsymbol{J}$を使って下記の式で与えられます。
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial x}\\
\frac{\partial N_1}{\partial y} && \frac{\partial N_2}{\partial y} &&
\frac{\partial N_3}{\partial y}\\
\end{bmatrix}
=
\boldsymbol{J}^{-1}
\begin{bmatrix}
\frac{\partial N_1}{\partial a} && \frac{\partial N_2}{\partial a} && \frac{\partial N_3}{\partial a} \\
\frac{\partial N_1}{\partial b} && \frac{\partial N_2}{\partial b} && \frac{\partial N_3}{\partial b} \\
\end{bmatrix}
=
\boldsymbol{J}^{-1}
\begin{bmatrix}
1 && 0 && -1 \\
0 && 1 && -1 \\
\end{bmatrix}
要素剛性マトリクス
要素剛性マトリクス$\boldsymbol{K_e}$は変数変換とガウス求積を使用して下記のように計算できます。
\begin{align}
\boldsymbol{K_e} &= t\int \int \boldsymbol{B}^T\boldsymbol{D}\boldsymbol{B} dxdy \\
&= t\int_{0}^1\int_{0}^{1-a} \boldsymbol{B}^T\boldsymbol{D}\boldsymbol{B} \begin{vmatrix} \boldsymbol{J} \end{vmatrix} dbda \\
&= t w \boldsymbol{B}^T\boldsymbol{D}\boldsymbol{B} \begin{vmatrix} \boldsymbol{J} \end{vmatrix}
\end{align}
\\
\quad
\\
w = 0.5 : 重み係数
三角形2次要素
三角形の2次要素で、節点数は6個、積分点は3点です。
正規化座標系
要素の積分を計算しやすくするために正規化座標系に変換します。

座標変換は形状関数$N_i$を使用した下記の式で与えられます。
\left\{
\begin{array}{ll}
x(a,b) = N_1 x_1 + N_2 x_2 + N_3 x_3 + N_4 x_4 + N_5 x_5 + N_6 x_6\\
y(a,b) = N_1 y_1 + N_2 y_2 + N_3 y_3 + N_4 y_4 + N_5 y_5 + N_6 y_6\\
\end{array}
\right.
\\
N_1 = a(2a-1) \\
N_2 = b(2b-1) \\
N_3 = (1 - a - b)(1 - 2a - 2b) \\
N_4 = 4ab \\
N_5 = 4b(1 - a - b) \\
N_6 = 4a(1 - a - b)
要素内の変位は下記の式で与えられます。
\\
\left\{
\begin{array}{ll}
u(a,b) = N_1 u_1 + N_2 u_2 + N_3 u_3 + N_4 u_4 + N_5 u_5 + N_6 u_6 \\
v(a,b) = N_1 v_1 + N_2 v_2 + N_3 v_3 + N_4 v_4 + N_5 v_5 + N_6 v_6 \\
\end{array}
\right.
Bマトリクス
要素内の変位の式から$\boldsymbol{B}$マトリクスは下記の式で与えられます。
\begin{bmatrix}
\epsilon_x \\
\epsilon_y \\
\gamma_{xy}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial u}{\partial x} \\
\frac{\partial v}{\partial y} \\
\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && 0 && \frac{\partial N_2}{\partial x} && 0 && \frac{\partial N_3}{\partial x} && 0 && \frac{\partial N_4}{\partial x} && 0 && \frac{\partial N_5}{\partial x} && 0 && \frac{\partial N_6}{\partial x} && 0 \\
0 && \frac{\partial N_1}{\partial y} && 0 && \frac{\partial N_2}{\partial y} && 0 && \frac{\partial N_3}{\partial y} && 0 && \frac{\partial N_4}{\partial y} && 0 && \frac{\partial N_5}{\partial y} && 0 && \frac{\partial N_6}{\partial y} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial x} &&
\frac{\partial N_2}{\partial y} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_3}{\partial x} &&
\frac{\partial N_4}{\partial y} && \frac{\partial N_4}{\partial x} &&
\frac{\partial N_5}{\partial y} && \frac{\partial N_5}{\partial x} &&
\frac{\partial N_6}{\partial y} && \frac{\partial N_6}{\partial x} &&
\end{bmatrix}
\begin{bmatrix}
u_1 \\
v_1 \\
u_2 \\
v_2 \\
u_3 \\
v_3 \\
u_4 \\
v_4 \\
u_5 \\
v_5 \\
u_6 \\
v_6
\end{bmatrix}
\\
\boldsymbol{B} =
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && 0 && \frac{\partial N_2}{\partial x} && 0 && \frac{\partial N_3}{\partial x} && 0 && \frac{\partial N_4}{\partial x} && 0 && \frac{\partial N_5}{\partial x} && 0 && \frac{\partial N_6}{\partial x} && 0 \\
0 && \frac{\partial N_1}{\partial y} && 0 && \frac{\partial N_2}{\partial y} && 0 && \frac{\partial N_3}{\partial y} && 0 && \frac{\partial N_4}{\partial y} && 0 && \frac{\partial N_5}{\partial y} && 0 && \frac{\partial N_6}{\partial y} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial x} &&
\frac{\partial N_2}{\partial y} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_3}{\partial x} &&
\frac{\partial N_4}{\partial y} && \frac{\partial N_4}{\partial x} &&
\frac{\partial N_5}{\partial y} && \frac{\partial N_5}{\partial x} &&
\frac{\partial N_6}{\partial y} && \frac{\partial N_6}{\partial x} &&
\end{bmatrix}
ヤコビ行列
ヤコビ行列$\boldsymbol{J}$は形状関数$N_i$を偏微分した下記の式で与えられます。
\begin{bmatrix}
\frac{\partial N_i}{\partial a} \\
\frac{\partial N_i}{\partial b}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial x}{\partial a} && \frac{\partial y}{\partial a} \\
\frac{\partial x}{\partial b} && \frac{\partial y}{\partial b}
\end{bmatrix}
\begin{bmatrix}
\frac{\partial N_i}{\partial x} \\
\frac{\partial N_i}{\partial y}
\end{bmatrix}
\\
\begin{bmatrix}
\frac{\partial N_i}{\partial a} \\
\frac{\partial N_i}{\partial b}
\end{bmatrix}
=
\boldsymbol{J}
\begin{bmatrix}
\frac{\partial N_i}{\partial x} \\
\frac{\partial N_i}{\partial y}
\end{bmatrix}
\\
\boldsymbol{J}(a,b)=
\begin{bmatrix}
\frac{\partial x}{\partial a} && \frac{\partial y}{\partial a} \\
\frac{\partial y}{\partial b} && \frac{\partial y}{\partial b}
\end{bmatrix}
=
\begin{bmatrix}
\sum_{i=1}^{6} \frac{\partial N_i}{\partial a} x_i && \sum_{i=1}^{6} \frac{\partial N_i}{\partial a} y_i \\
\sum_{i=1}^{6} \frac{\partial N_i}{\partial b} x_i && \sum_{i=1}^{6} \frac{\partial N_i}{\partial b} y_i
\end{bmatrix}
\\
\begin{align}
&\frac{\partial N_1}{\partial a} = 4a - 1 & & \frac{\partial N_1}{\partial b} = 0 \\
&\frac{\partial N_2}{\partial a} = 0 & & \frac{\partial N_2}{\partial b} = 4b - 1 \\
&\frac{\partial N_3}{\partial a} = -3 + 4a + 4b & & \frac{\partial N_3}{\partial b} = -3 + 4a + 4b \\
&\frac{\partial N_4}{\partial a} = 4b & & \frac{\partial N_4}{\partial b} = 4a \\
&\frac{\partial N_5}{\partial a} = -4b & & \frac{\partial N_5}{\partial b} = 4 - 4a - 8b \\
&\frac{\partial N_6}{\partial a} = 4 -8a - 4b & & \frac{\partial N_6}{\partial b} = -4a
\end{align}
形状関数の偏微分
形状関数$N_i$の$x$,$y$に関する偏微分はヤコビ行列$\boldsymbol{J}$を使って下記の式で与えられます。
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial x} && \frac{\partial N_4}{\partial x} &&
\frac{\partial N_5}{\partial x} && \frac{\partial N_6}{\partial x} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_2}{\partial y} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_4}{\partial y} &&
\frac{\partial N_5}{\partial y} && \frac{\partial N_6}{\partial y} \\
\end{bmatrix}
=
\boldsymbol{J}^{-1}
\begin{bmatrix}
\frac{\partial N_1}{\partial a} && \frac{\partial N_2}{\partial a} && \frac{\partial N_3}{\partial a} && \frac{\partial N_4}{\partial a} && \frac{\partial N_5}{\partial a} && \frac{\partial N_6}{\partial a} \\
\frac{\partial N_1}{\partial b} && \frac{\partial N_2}{\partial b} && \frac{\partial N_3}{\partial b} && \frac{\partial N_4}{\partial b} && \frac{\partial N_5}{\partial b} && \frac{\partial N_6}{\partial b} \\
\end{bmatrix}
=
\boldsymbol{J}^{-1}
\begin{bmatrix}
4a - 1 && 0 && -3 + 4a + 4b && 4b && -4b && 4 -8a - 4b\\
0 && 4b - 1 && -3 + 4a + 4b && 4a && 4 - 4a - 8b && -4a\\
\end{bmatrix}
要素剛性マトリクス
要素剛性マトリクス$\boldsymbol{K_e}$は変数変換とガウス求積を使用して下記のように計算できます。
\begin{align}
\boldsymbol{K_e} &= t\int \int \boldsymbol{B}^T(x,y)\boldsymbol{D}\boldsymbol{B}(x,y) dxdy \\
&= t\int_{-1}^1\int_{-1}^{1} \boldsymbol{B}^T(a,b)\boldsymbol{D}\boldsymbol{B}(a,b) \begin{vmatrix} \boldsymbol{J}(a,b) \end{vmatrix} dadb \\
&= \sum_{i=1}^3 w_i \boldsymbol{B}^T(a_i,b_i)\boldsymbol{D}\boldsymbol{B}(a_i,b_i) \begin{vmatrix} \boldsymbol{J}(a_i,b_i) \end{vmatrix}
\end{align}
\\
w_i : 重み係数
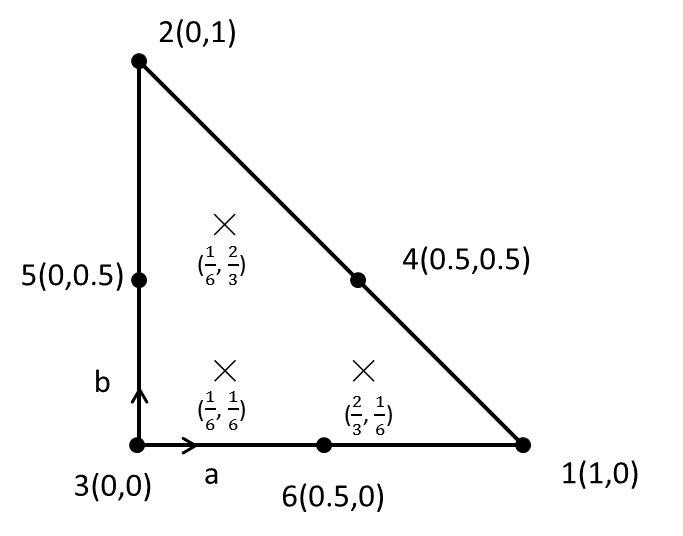
積分点の位置と重み係数
|$i$ |$w_i$ |$a_i$ |$b_j$ |
|---|---|---|---|---|
|1 |$\frac{1}{6}$ |$\frac{1}{6}$ |$\frac{1}{6}$ |
|2 |$\frac{1}{6}$ |$\frac{2}{3}$ |$\frac{1}{6}$ |
|3 |$\frac{1}{6}$ |$\frac{1}{6}$ |$\frac{2}{3}$ |
四角形要素
四角形要素は4節点で積分点は4点になります。
正規化座標系
要素の積分を計算しやすくするために正規化座標系に変換します。

座標変換は形状関数$N_i$を使用した下記の式で与えられます。
\left\{
\begin{array}{ll}
x(a,b) = N_1 x_1 + N_2 x_2 + N_3 x_3 + N_4 x_4\\
y(a,b) = N_1 y_1 + N_2 y_2 + N_3 y_3 + N_4 y_4\\
\end{array}
\right.
\\
N_1 = \frac{1}{4}(1-a)(1-b) \\
N_2 = \frac{1}{4}(1+a)(1-b) \\
N_3 = \frac{1}{4}(1+a)(1+b) \\
N_4 = \frac{1}{4}(1-a)(1+b)
要素内の変位は下記の式で与えられます。
\\
\left\{
\begin{array}{ll}
u(a,b) = N_1 u_1 + N_2 u_2 + N_3 u_3 + N_4 u_4 \\
v(a,b) = N_1 v_1 + N_2 v_2 + N_3 v_3 + N_4 v_4\\
\end{array}
\right.
Bマトリクス
要素内の変位の式から$\boldsymbol{B}$マトリクスは下記の式で与えられます。
\begin{bmatrix}
\epsilon_x \\
\epsilon_y \\
\gamma_{xy}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial u}{\partial x} \\
\frac{\partial v}{\partial y} \\
\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}
\end{bmatrix}
\\
=
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && 0 && \frac{\partial N_2}{\partial x} && 0 && \frac{\partial N_3}{\partial x} && 0 && \frac{\partial N_4}{\partial x} && 0 \\
0 && \frac{\partial N_1}{\partial y} && 0 && \frac{\partial N_2}{\partial y} && 0 && \frac{\partial N_3}{\partial y} && 0 && \frac{\partial N_4}{\partial y} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial x} &&
\frac{\partial N_2}{\partial y} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_3}{\partial x} &&
\frac{\partial N_4}{\partial y} && \frac{\partial N_4}{\partial x}
\end{bmatrix}
\begin{bmatrix}
u_1 \\
v_1 \\
u_2 \\
v_2 \\
u_3 \\
v_3 \\
u_4 \\
v_4
\end{bmatrix}
\\
\boldsymbol{B} =
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && 0 && \frac{\partial N_2}{\partial x} && 0 && \frac{\partial N_3}{\partial x} && 0 && \frac{\partial N_4}{\partial x} && 0 \\
0 && \frac{\partial N_1}{\partial y} && 0 && \frac{\partial N_2}{\partial y} && 0 && \frac{\partial N_3}{\partial y} && 0 && \frac{\partial N_4}{\partial y} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial x} &&
\frac{\partial N_2}{\partial y} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_3}{\partial x} &&
\frac{\partial N_4}{\partial y} && \frac{\partial N_4}{\partial x}
\end{bmatrix}
ヤコビ行列
ヤコビ行列$\boldsymbol{J}$は形状関数$N_i$を偏微分した下記の式で与えられます。
\begin{bmatrix}
\frac{\partial N_i}{\partial a} \\
\frac{\partial N_i}{\partial b}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial x}{\partial a} && \frac{\partial y}{\partial a} \\
\frac{\partial x}{\partial b} && \frac{\partial y}{\partial b}
\end{bmatrix}
\begin{bmatrix}
\frac{\partial N_i}{\partial x} \\
\frac{\partial N_i}{\partial y}
\end{bmatrix}
\\
\begin{bmatrix}
\frac{\partial N_i}{\partial a} \\
\frac{\partial N_i}{\partial b}
\end{bmatrix}
=
\boldsymbol{J}
\begin{bmatrix}
\frac{\partial N_i}{\partial x} \\
\frac{\partial N_i}{\partial y}
\end{bmatrix}
\\
\boldsymbol{J}(a,b)=
\begin{bmatrix}
\frac{\partial x}{\partial a} && \frac{\partial y}{\partial a} \\
\frac{\partial y}{\partial b} && \frac{\partial y}{\partial b}
\end{bmatrix}
=
\begin{bmatrix}
\sum_{i=1}^{4} \frac{\partial N_i}{\partial a} x_i && \sum_{i=1}^{4} \frac{\partial N_i}{\partial a} y_i \\
\sum_{i=1}^{4} \frac{\partial N_i}{\partial b} x_i && \sum_{i=1}^{4} \frac{\partial N_i}{\partial b} y_i
\end{bmatrix}
\\
\begin{align}
&\frac{\partial N_1}{\partial a} = -\frac{1-b}{4} & & \frac{\partial N_1}{\partial b} = -\frac{1-a}{4}\\
&\frac{\partial N_2}{\partial a} = \frac{1-b}{4} & & \frac{\partial N_2}{\partial b} = -\frac{1+a}{4}\\
&\frac{\partial N_3}{\partial a} = \frac{1+b}{4} & & \frac{\partial N_3}{\partial b} = \frac{1+a}{4}\\
&\frac{\partial N_4}{\partial a} = -\frac{1+b}{4} & & \frac{\partial N_4}{\partial b} = \frac{1-a}{4}\\
\end{align}
形状関数の偏微分
形状関数$N_i$の$x$,$y$に関する偏微分はヤコビ行列$\boldsymbol{J}$を使って下記の式で与えられます。
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial x} && \frac{\partial N_4}{\partial x} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_2}{\partial y} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_4}{\partial y} \\
\end{bmatrix}
=
\boldsymbol{J}^{-1}
\begin{bmatrix}
\frac{\partial N_1}{\partial a} && \frac{\partial N_2}{\partial a} && \frac{\partial N_3}{\partial a} && \frac{\partial N_4}{\partial a} \\
\frac{\partial N_1}{\partial b} && \frac{\partial N_2}{\partial b} && \frac{\partial N_3}{\partial b} && \frac{\partial N_4}{\partial b} \\
\end{bmatrix}
=
\boldsymbol{J}^{-1}
\begin{bmatrix}
-\frac{1-b}{4} && \frac{1-b}{4} && \frac{1+b}{4} && -\frac{1+b}{4} \\
-\frac{1-a}{4} && -\frac{1+a}{4} && \frac{1+a}{4} && \frac{1-a}{4}\\
\end{bmatrix}
要素剛性マトリクス
要素剛性マトリクス$\boldsymbol{K_e}$は変数変換とガウス求積を使用して下記のように計算できます。
\begin{align}
\boldsymbol{K_e} &= t\int \int \boldsymbol{B}^T(x,y)\boldsymbol{D}\boldsymbol{B}(x,y) dxdy \\
&= t\int_{-1}^1\int_{-1}^{1} \boldsymbol{B}^T(a,b)\boldsymbol{D}\boldsymbol{B}(a,b) \begin{vmatrix} \boldsymbol{J}(a,b) \end{vmatrix} dadb \\
&= \sum_{i=1}^2 \sum_{j=1}^2 w_i w_j \boldsymbol{B}^T(a_i,b_i)\boldsymbol{D}\boldsymbol{B}(a_i,b_i) \begin{vmatrix} \boldsymbol{J}(a_i,b_i) \end{vmatrix}
\end{align}
\\
w_i : 重み係数
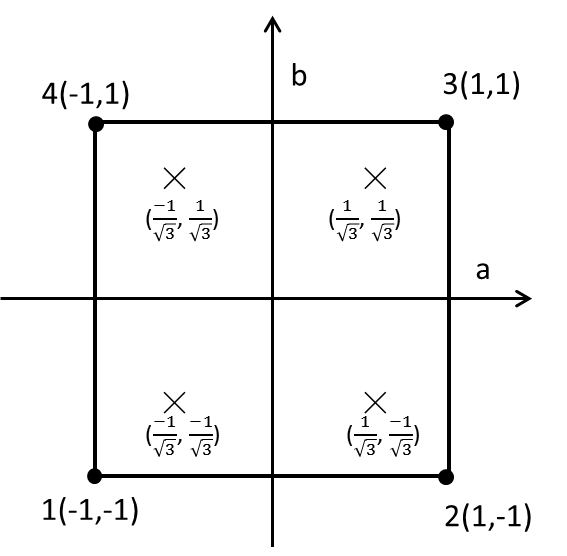
積分点の位置と重み係数
|$i$ |$j$ |$w_i$ |$w_j$ |$a_i$ |$b_j$ |
|---|---|---|---|---|---|---|
|1 |1 |1.0 |1.0 |$-\frac{1}{\sqrt{3}}$ |$-\frac{1}{\sqrt{3}}$ |
|1 |2 |1.0 |1.0 |$\frac{1}{\sqrt{3}}$ |$-\frac{1}{\sqrt{3}}$ |
|2 |1 |1.0 |1.0 |$\frac{1}{\sqrt{3}}$ |$\frac{1}{\sqrt{3}}$ |
|2 |2 |1.0 |1.0 |$-\frac{1}{\sqrt{3}}$ |$\frac{1}{\sqrt{3}}$ |
四角形2次要素
四角形の2次要素で8節点で積分点は9点になります。
正規化座標系
要素の積分を計算しやすくするために正規化座標系に変換します。

座標変換は形状関数$N_i$を使用した下記の式で与えられます。
\left\{
\begin{array}{ll}
x(a,b) = N_1 x_1 + N_2 x_2 + N_3 x_3 + N_4 x_4 + N_5 x_5 + N_6 x_6 + N_7 x_7 + N_8 x_8 \\
y(a,b) = N_1 y_1 + N_2 y_2 + N_3 y_3 + N_4 y_4 + N_5 y_5 + N_6 y_6 + N_7 y_7 + N_8 y_8 \\
\end{array}
\right.
\\
\begin{align}
N_1 &= \frac{1}{4}(1-a)(1-b)(-a-b-1) \\
N_2 &= \frac{1}{4}(1+a)(1-b)(a-b-1) \\
N_3 &= \frac{1}{4}(1+a)(1+b)(a+b-1) \\
N_4 &= \frac{1}{4}(1-a)(1+b)(-a+b-1) \\
N_5 &= \frac{1}{2}(1-a^2)(1-b) \\
N_6 &= \frac{1}{2}(1-b^2)(1+a) \\
N_7 &= \frac{1}{2}(1-a^2)(1+b) \\
N_8 &= \frac{1}{2}(1-b^2)(1-a)
\end{align}
要素内の変位は下記の式で与えられます。
\\
\left\{
\begin{array}{ll}
u(a,b) = N_1 u_1 + N_2 u_2 + N_3 u_3 + N_4 u_4 + N_5 u_5 + N_6 u_6 + N_7 u_7 + N_8 u_8 \\
v(a,b) = N_1 v_1 + N_2 v_2 + N_3 v_3 + N_4 v_4 + N_5 v_5 + N_6 v_6 + N_7 v_7 + N_8 vu_8 \\
\end{array}
\right.
Bマトリクス
要素内の変位の式から$\boldsymbol{B}$マトリクスは下記の式で与えられます。
\boldsymbol{B} =
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && 0 && \frac{\partial N_2}{\partial x} && 0 && \frac{\partial N_3}{\partial x} && 0 && \frac{\partial N_4}{\partial x} && 0 && \frac{\partial N_5}{\partial x} && 0 && \frac{\partial N_6}{\partial x} && 0 && \frac{\partial N_7}{\partial x} && 0 && \frac{\partial N_8}{\partial x} && 0 \\
0 && \frac{\partial N_1}{\partial y} && 0 && \frac{\partial N_2}{\partial y} && 0 && \frac{\partial N_3}{\partial y} && 0 && \frac{\partial N_4}{\partial y} && 0 && \frac{\partial N_5}{\partial y} && 0 && \frac{\partial N_6}{\partial y} && 0 && \frac{\partial N_7}{\partial y} && 0 && \frac{\partial N_8}{\partial y} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial x} &&
\frac{\partial N_2}{\partial y} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_3}{\partial x} &&
\frac{\partial N_4}{\partial y} && \frac{\partial N_4}{\partial x} &&
\frac{\partial N_5}{\partial y} && \frac{\partial N_5}{\partial x} &&
\frac{\partial N_6}{\partial y} && \frac{\partial N_6}{\partial x} &&
\frac{\partial N_7}{\partial y} && \frac{\partial N_7}{\partial x} &&
\frac{\partial N_8}{\partial y} && \frac{\partial N_8}{\partial x}
\end{bmatrix}
ヤコビ行列
ヤコビ行列$\boldsymbol{J}$は形状関数$N_i$を偏微分した下記の式で与えられます。
\begin{bmatrix}
\frac{\partial N_i}{\partial a} \\
\frac{\partial N_i}{\partial b}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial x}{\partial a} && \frac{\partial y}{\partial a} \\
\frac{\partial x}{\partial b} && \frac{\partial y}{\partial b}
\end{bmatrix}
\begin{bmatrix}
\frac{\partial N_i}{\partial x} \\
\frac{\partial N_i}{\partial y}
\end{bmatrix}
\\
\begin{bmatrix}
\frac{\partial N_i}{\partial a} \\
\frac{\partial N_i}{\partial b}
\end{bmatrix}
=
\boldsymbol{J}
\begin{bmatrix}
\frac{\partial N_i}{\partial x} \\
\frac{\partial N_i}{\partial y}
\end{bmatrix}
\\
\boldsymbol{J}(a,b)=
\begin{bmatrix}
\frac{\partial x}{\partial a} && \frac{\partial y}{\partial a} \\
\frac{\partial y}{\partial b} && \frac{\partial y}{\partial b}
\end{bmatrix}
=
\begin{bmatrix}
\sum_{i=1}^{8} \frac{\partial N_i}{\partial a} x_i && \sum_{i=1}^{8} \frac{\partial N_i}{\partial a} y_i \\
\sum_{i=1}^{8} \frac{\partial N_i}{\partial b} x_i && \sum_{i=1}^{8} \frac{\partial N_i}{\partial b} y_i
\end{bmatrix}
\\
\begin{align}
\frac{\partial N_1}{\partial a} &= \frac{1}{4}(1-b)(2a+b) \quad &\frac{\partial N_1}{\partial b} &= \frac{1}{4}(1-a)(a+2b) \\
\frac{\partial N_2}{\partial a} &= \frac{1}{4}(1-b)(2a-b) \quad &\frac{\partial N_2}{\partial b} &= \frac{1}{4}(1+a)(-a+2b) \\
\frac{\partial N_3}{\partial a} &= \frac{1}{4}(1+b)(2a+b) \quad &\frac{\partial N_3}{\partial b} &= \frac{1}{4}(1+a)(a+2b) \\
\frac{\partial N_4}{\partial a} &= \frac{1}{4}(1+b)(2a-b) \quad &\frac{\partial N_4}{\partial b} &= \frac{1}{4}(1-a)(-a+2b) \\
\frac{\partial N_5}{\partial a} &= -a(1-b) \quad &\frac{\partial N_5}{\partial b} &= -\frac{1}{2}(1-a^2) \\
\frac{\partial N_6}{\partial a} &= \frac{1}{2}(1-b^2) \quad &\frac{\partial N_6}{\partial b} &= -b(1+a) \\
\frac{\partial N_7}{\partial a} &= -a(1+b) \quad &\frac{\partial N_7}{\partial b} &= \frac{1}{2}(1-a^2) \\
\frac{\partial N_8}{\partial a} &= -\frac{1}{2}(1-b^2) \quad &\frac{\partial N_8}{\partial b} &= -b(1-a)
\end{align}
形状関数の偏微分
形状関数$N_i$の$x$,$y$に関する偏微分はヤコビ行列$\boldsymbol{J}$を使って下記の式で与えられます。
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial x} && \frac{\partial N_4}{\partial x} &&
\frac{\partial N_5}{\partial x} && \frac{\partial N_6}{\partial x} &&
\frac{\partial N_7}{\partial x} && \frac{\partial N_8}{\partial x} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_2}{\partial y} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_4}{\partial y} &&
\frac{\partial N_5}{\partial y} && \frac{\partial N_6}{\partial y} &&
\frac{\partial N_7}{\partial y} && \frac{\partial N_8}{\partial y} \\
\end{bmatrix}
=
\boldsymbol{J}^{-1}
\begin{bmatrix}
\frac{\partial N_1}{\partial a} && \frac{\partial N_2}{\partial a} && \frac{\partial N_3}{\partial a} && \frac{\partial N_4}{\partial a} && \frac{\partial N_5}{\partial a} && \frac{\partial N_6}{\partial a} && \frac{\partial N_7}{\partial a} && \frac{\partial N_7}{\partial a}\\
\frac{\partial N_1}{\partial b} && \frac{\partial N_2}{\partial b} && \frac{\partial N_3}{\partial b} && \frac{\partial N_4}{\partial b} && \frac{\partial N_5}{\partial b} && \frac{\partial N_6}{\partial b} && \frac{\partial N_7}{\partial b} && \frac{\partial N_8}{\partial b} \\
\end{bmatrix}
要素剛性マトリクス
要素剛性マトリクス$\boldsymbol{K_e}$は変数変換とガウス求積を使用して下記のように計算できます。
\begin{align}
\boldsymbol{K_e} &= t\int \int \boldsymbol{B}^T(x,y)\boldsymbol{D}\boldsymbol{B}(x,y) dxdy \\
&= t\int_{-1}^1\int_{-1}^{1} \boldsymbol{B}^T(a,b)\boldsymbol{D}\boldsymbol{B}(a,b) \begin{vmatrix} \boldsymbol{J}(a,b) \end{vmatrix} dadb \\
&= \sum_{i=1}^3 \sum_{j=1}^3 w_i w_j \boldsymbol{B}^T(a_i,b_i)\boldsymbol{D}\boldsymbol{B}(a_i,b_i) \begin{vmatrix} \boldsymbol{J}(a_i,b_i) \end{vmatrix}
\end{align}
\\
w_i : 重み係数
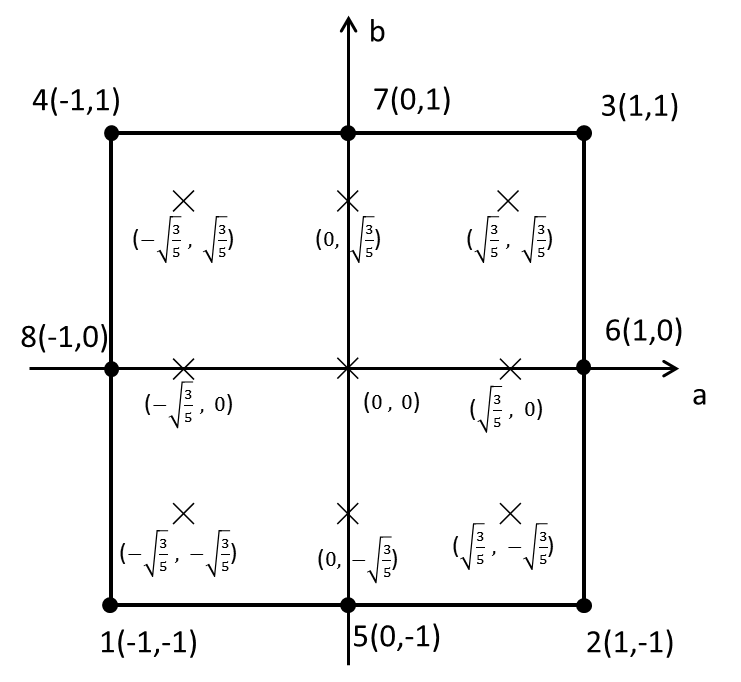
積分点の位置と重み係数
|$i$ |$j$ |$w_i$ |$w_j$ |$a_i$ |$b_j$ |
|---|---|---|---|---|---|---|
|1 |1 |$\frac{5}{9}$ |$\frac{5}{9}$ |$-\sqrt{\frac{3}{5}}$ |$-\sqrt{\frac{3}{5}}$ |
|1 |2 |$\frac{8}{9}$ |$\frac{5}{9}$ |$0$ |$-\sqrt{\frac{3}{5}}$ |
|1 |3 |$\frac{5}{9}$ |$\frac{5}{9}$ |$\sqrt{\frac{3}{5}}$ |$-\sqrt{\frac{3}{5}}$ |
|2 |1 |$\frac{5}{9}$ |$\frac{8}{9}$ |$-\sqrt{\frac{3}{5}}$ |$0$ |
|2 |2 |$\frac{8}{9}$ |$\frac{8}{9}$ |$0$ |$0$ |
|2 |3 |$\frac{5}{9}$ |$\frac{8}{9}$ |$\sqrt{\frac{3}{5}}$ |$0$ |
|3 |1 |$\frac{5}{9}$ |$\frac{5}{9}$ |$-\sqrt{\frac{3}{5}}$ |$\sqrt{\frac{3}{5}}$ |
|3 |2 |$\frac{8}{9}$ |$\frac{5}{9}$ |$0$ |$\sqrt{\frac{3}{5}}$ |
|3 |3 |$\frac{5}{9}$ |$\frac{5}{9}$ |$\sqrt{\frac{3}{5}}$ |$\sqrt{\frac{3}{5}}$ |
トラス要素
2節点で定ひずみとなる要素です。積分点は1点だけです。
座標変換
トラス要素は他の要素と違い、1次元の要素なので、座標変換が必要になります。
全体座標系をxy座標としてトラス要素と並行となるx'y'座標系に座標変換します。
座標変換の式は下記のように表せます。

\begin{bmatrix}
x' \\
y'
\end{bmatrix}
=
\begin{bmatrix}
cos\theta && sin\theta \\
-sin\theta && cos\theta
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}
正規化座標系
要素の積分を計算しやすくするために正規化座標系に変換します。

座標変換は形状関数$N_i$を使用した下記の式で与えられます。
x'(a) = N_1 x'_1 + N_2 x'_2\\
\\
\begin{align}
N_1 &= \frac{1}{2}(1-a) \\
N_2 &= \frac{1}{2}(1+a) \\
\end{align}
要素内の変位は下記の式で与えられます。
\\
u'(a) = N_1 u'_1 + N_2 u'_2 \\
Dマトリクス
トラス要素は1次元なので、応力とひずみの関係式は
\sigma_{x'} = E \epsilon_{x'}
になり、$\boldsymbol{D} = E$となります。しかし、2次元のひずみ状態で考えているので、不要な部分は$0$で埋めた3×3の行列にしておきます。
\boldsymbol{D} =
\begin{bmatrix}
E && 0 && 0 \\
0 && 0 && 0 \\
0 && 0 && 0
\end{bmatrix}
Bマトリクス
要素内の変位の式から$\boldsymbol{B}$マトリクスは下記の式で与えられます。
\begin{bmatrix}
\epsilon_{x'} \\
\epsilon_{y'} \\
\gamma_{x'y'}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial u'}{\partial x'} \\
\frac{\partial v'}{\partial y'} \\
\frac{\partial u'}{\partial y'} + \frac{\partial v'}{\partial x'}
\end{bmatrix}
\\
=
\begin{bmatrix}
\frac{\partial N_1}{\partial x'} && 0 && \frac{\partial N_2}{\partial x'} && 0 \\
0 && 0 && 0 && 0 \\
0 && 0 && 0 && 0
\end{bmatrix}
\begin{bmatrix}
u'_1 \\
v'_1 \\
u'_2 \\
v'_2 \\
\end{bmatrix}
\\
\boldsymbol{B} =
\begin{bmatrix}
\frac{\partial N_1}{\partial x'} && 0 && \frac{\partial N_2}{\partial x'} && 0 \\
0 && 0 && 0 && 0 \\
0 && 0 && 0 && 0
\end{bmatrix}
形状関数の偏微分
形状関数の偏微分は下記のように計算することができます。
\begin{align}
\frac{dN_i}{d x'} &= \frac{d N_i}{d a} \frac{d a}{d x'} = \frac{d N_i}{d a} (\frac{d x'}{d a})^{-1} \\
\frac{d x'}{d a} &= \frac{1}{2}(-x'_1 + x'_2) \\
\frac{dN_1}{d x'} &= -\frac{1}{-x'_1 + x'_2} \\
\frac{dN_2}{d x'} &= \frac{1}{-x'_1 + x'_2}
\end{align}
要素剛性マトリクス
x'y'座標系における要素剛性マトリクス$\boldsymbol{K'_e}$は変数変換とガウス求積を使用して下記のように計算できます。
\begin{align}
\boldsymbol{K'_e} &= A \int \boldsymbol{B}^T\boldsymbol{D}\boldsymbol{B} dx' \\
&= A \int_{-1}^{1} \boldsymbol{B}^T\boldsymbol{D}\boldsymbol{B} \frac{d x'}{d a} da \\
&= Aw \boldsymbol{B}^T\boldsymbol{D}\boldsymbol{B} \frac{d x'}{d a}
\end{align}
\\
A : 断面積 \\
w = 2.0 : 重み係数
積分点の位置

ここで、要素剛性マトリクスはx'y'座標系で表されているので、xy座標系に変換します。
x'y'座標系における節点に負荷する荷重を$\boldsymbol{f'}$、節点の変位を$\boldsymbol{\tilde{u}'}$とおくと、
\boldsymbol{f'} = \boldsymbol{K'_e} \boldsymbol{\tilde{u}'} \\
で表すことができます。ここで、$\boldsymbol{f'}$、$\boldsymbol{\tilde{u}'}$は座標変換行列$\boldsymbol{T}$により、xy座標系の$\boldsymbol{f}$、$\boldsymbol{\tilde{u}}$に変換することができます。
\boldsymbol{f'} = \boldsymbol{T}\boldsymbol{f} \\
\boldsymbol{\tilde{u}'} = \boldsymbol{T}\boldsymbol{\tilde{u}} \\
\boldsymbol{T} =
\begin{bmatrix}
cos\theta && sin\theta && 0 && 0 \\
-sin\theta && cos\theta && 0 && 0 \\
0 && 0 && cos\theta && sin\theta \\
0 && 0 &&-sin\theta && cos\theta
\end{bmatrix}
この式を代入すると下記のように表せます。
\boldsymbol{f'} = \boldsymbol{K'_e} \boldsymbol{\tilde{u}'} \\
\boldsymbol{T}\boldsymbol{f} = \boldsymbol{K'_e}\boldsymbol{T}\boldsymbol{\tilde{u}} \\
\boldsymbol{f} = \boldsymbol{T}^T \boldsymbol{K'_e} \boldsymbol{T} \boldsymbol{\tilde{u}}
y座標系における要素剛性マトリクス$\boldsymbol{K_e}$は下記の式で求めることができます。
\boldsymbol{K_e} = \boldsymbol{T}^T \boldsymbol{K'_e} \boldsymbol{T}
ひずみ
有限要素法により、要素の節点変位を求めた後はひずみ$\boldsymbol{\epsilon}$を求める必要があります。
トラス要素以外では$\boldsymbol{\epsilon} = \boldsymbol{B}\boldsymbol{\tilde{u}}$で求めることができますが、トラス要素では座標変換を使ったので、
ひずみ$\boldsymbol{\epsilon'}$をxy座標系に座標変換する必要があります。
ひずみの座標変換は下記の式で与えられます。
\boldsymbol{\epsilon'} = \boldsymbol{R} \boldsymbol{A} \boldsymbol{R}^{-1} \boldsymbol{\epsilon} \\
\boldsymbol{R} =
\begin{bmatrix}
1 && 0 && 0 \\
0 && 1 && 0 \\
0 && 0 && 2
\end{bmatrix}
\\
\boldsymbol{A} =
\begin{bmatrix}
cos^2\theta && sin^2\theta && 2sin\theta cos\theta \\
sin^2\theta && cos^2\theta && -2sin\theta cos\theta \\
-sin\theta cos\theta && sin\theta cos\theta && cos^2\theta - sin^2\theta
\end{bmatrix}
導出についてはこちらを参照ください。
この変換式を用いると、$\boldsymbol{\epsilon}$を求めることができます。
\boldsymbol{\epsilon'} = \boldsymbol{B} \boldsymbol{\tilde{u}'} \\
\boldsymbol{R} \boldsymbol{A} \boldsymbol{R}^{-1} \boldsymbol{\epsilon} =
\boldsymbol{B} \boldsymbol{T} \boldsymbol{\tilde{u}} \\
\boldsymbol{\epsilon} = \boldsymbol{R} \boldsymbol{A}^{-1} \boldsymbol{R}^{-1} \boldsymbol{B} \boldsymbol{T} \boldsymbol{\tilde{u}}
応力
応力もひずみと同様に座標変換する必要があります。
応力の座標変換は下記の式で与えられます。
\boldsymbol{\sigma'} = \boldsymbol{A} \boldsymbol{\sigma}
求まったひずみ$\boldsymbol{\epsilon}$から下記の式を使って求めることができます。
\boldsymbol{\sigma'} = \boldsymbol{D} \boldsymbol{\epsilon'} \\
\boldsymbol{A} \boldsymbol{\sigma} = \boldsymbol{D} \boldsymbol{R} \boldsymbol{A} \boldsymbol{R}^{-1} \boldsymbol{\epsilon} \\
\boldsymbol{\sigma} = \boldsymbol{A}^{-1} \boldsymbol{D} \boldsymbol{R} \boldsymbol{A} \boldsymbol{R}^{-1} \boldsymbol{\epsilon}
トラス2次要素
トラスの2次要素で節点は3個、積分点は2点になります。
座標変換
トラス要素と同様にまずはx'y'座標系に座標変換します。

\begin{bmatrix}
x' \\
y'
\end{bmatrix}
=
\begin{bmatrix}
cos\theta && sin\theta \\
-sin\theta && cos\theta
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}
正規化座標系
要素の積分を計算しやすくするために正規化座標系に変換します。

座標変換は形状関数$N_i$を使用した下記の式で与えられます。
x'(a) = N_1 x'_1 + N_2 x'_2 + N_3 x'_3\\
\\
\begin{align}
N_1 &= \frac{a}{2}(a-1) \\
N_2 &= 1-a^2 \\
N_3 &= \frac{a}{2}(a+1)
\end{align}
要素内の変位は下記の式で与えられます。
\\
u'(a) = N_1 u'_1 + N_2 u'_2 + N_3 u'_3\\
Dマトリクス
トラス要素と同様に下記の式で表されます。
\boldsymbol{D} =
\begin{bmatrix}
E && 0 && 0 \\
0 && 0 && 0 \\
0 && 0 && 0
\end{bmatrix}
Bマトリクス
要素内の変位の式から$\boldsymbol{B}$マトリクスは下記の式で与えられます。
\begin{bmatrix}
\epsilon_{x'} \\
\epsilon_{y'} \\
\gamma_{x'y'}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial u'}{\partial x'} \\
\frac{\partial v'}{\partial y'} \\
\frac{\partial u'}{\partial y'} + \frac{\partial v'}{\partial x'}
\end{bmatrix}
\\
=
\begin{bmatrix}
\frac{\partial N_1}{\partial x'} && 0 && \frac{\partial N_2}{\partial x'} && 0 && \frac{\partial N_3}{\partial x'} && 0 \\
0 && 0 && 0 && 0 && 0 && 0 \\
0 && 0 && 0 && 0 && 0 && 0
\end{bmatrix}
\begin{bmatrix}
u'_1 \\
v'_1 \\
u'_2 \\
v'_2 \\
u'_3 \\
v'_3 \\
\end{bmatrix}
\\
\boldsymbol{B} =
\begin{bmatrix}
\frac{\partial N_1}{\partial x'} && 0 && \frac{\partial N_2}{\partial x'} && 0 && \frac{\partial N_3}{\partial x'} && 0 \\
0 && 0 && 0 && 0 && 0 && 0 \\
0 && 0 && 0 && 0 && 0 && 0
\end{bmatrix}
形状関数の偏微分
形状関数の偏微分は下記のように計算することができます。
\begin{align}
\frac{dN_i}{dx'} &= \frac{d N_i}{d a} \frac{da}{dx'} = \frac{dN_i}{da} (\frac{dx'}{da})^{-1} \\
\frac{dN_1}{da} &= a-\frac{1}{2} \\
\frac{dN_2}{da} &= -2a \\
\frac{dN_3}{da} &= a+\frac{1}{2} \\
\frac{dx'}{da} &= (a-\frac{1}{2})x'_1 -2ax'_2 + (a+\frac{1}{2})x'_3
\end{align}
要素剛性マトリクス
x'y'座標系における要素剛性マトリクス$\boldsymbol{K'_e}$は変数変換とガウス求積を使用して下記のように計算できます。
\begin{align}
\boldsymbol{K'_e} &= A \int \boldsymbol{B}^T\boldsymbol{D}\boldsymbol{B} dx' \\
&= A \int_{-1}^{1} \boldsymbol{B}(a)^T\boldsymbol{D}\boldsymbol{B}(a) \frac{dx'}{da} da \\
&= A\sum_{i=1}^2 w_i \boldsymbol{B}(a_i)^T\boldsymbol{D}\boldsymbol{B}(a_i) \frac{d x'}{da}(a_i)
\end{align}
\\
A : 断面積 \\
w_i : 重み係数
積分点の位置と重み係数
|$i$ |$w_i$ |$a_i$ |
|---|---|---|---|
|1 |$1.0$ |-$\sqrt{\frac{1}{3}}$ |
|2 |$1.0$ |$\sqrt{\frac{1}{3}}$ |

ここで、トラス要素と同様に要素剛性マトリクスはx'y'座標系で表されているので、xy座標系に変換します。
\boldsymbol{K_e} = \boldsymbol{T}^T \boldsymbol{K'_e} \boldsymbol{T} \\
\boldsymbol{T} =
\begin{bmatrix}
cos\theta && sin\theta && 0 && 0 && 0 && 0 \\
-sin\theta && cos\theta && 0 && 0 && 0 && 0 \\
0 && 0 && cos\theta && sin\theta && 0 && 0 \\
0 && 0 && -sin\theta && cos\theta && 0 && 0 \\
0 && 0 && 0 && 0 && cos\theta && sin\theta \\
0 && 0 && 0 && 0 && -sin\theta && cos\theta
\end{bmatrix}
ひずみ
トラス要素と同様の式で求められます。
\boldsymbol{\epsilon} = \boldsymbol{R} \boldsymbol{A}^{-1} \boldsymbol{R}^{-1} \boldsymbol{B} \boldsymbol{T} \boldsymbol{\tilde{u}} \\
\boldsymbol{R} =
\begin{bmatrix}
1 && 0 && 0 \\
0 && 1 && 0 \\
0 && 0 && 2
\end{bmatrix}
\\
\boldsymbol{A} =
\begin{bmatrix}
cos^2\theta && sin^2\theta && 2sin\theta cos\theta \\
sin^2\theta && cos^2\theta && -2sin\theta cos\theta \\
-sin\theta cos\theta && sin\theta cos\theta && cos^2\theta - sin^2\theta
\end{bmatrix}
応力
トラス要素と同様の式で求められます。
\boldsymbol{\sigma} = \boldsymbol{A}^{-1} \boldsymbol{D} \boldsymbol{R} \boldsymbol{A} \boldsymbol{R}^{-1} \boldsymbol{\epsilon}
