概要
有限要素法の弾塑性解析をPythonで実装する(1次元トラス要素)の続きです。
前回の投稿では線形硬化として材料特性が下記の図で表される状態のリターンマッピング法を実装しました。
しかし、材料は下記のように非線形になることが一般的です。
そこで、今回は下記の図のように多直線で近似した場合の非線形硬化を考慮したリターンマッピング法をPythonで実装してみます。
前の記事からの変更点はリターンマッピング法の違いのみです。
そのため、リターンマッピング法以外の処理はまとめの形で記載します。
また、この記事では下記の例題を解くサンプルを実装してみます。
なお、本稿のプログラムはAbaqus内部の処理と差があります。詳しくは余談の項目を参照ください。
全体の処理
解く非線形方程式
\boldsymbol{Q}(\tilde{\boldsymbol{U}}) = \boldsymbol{f} \\
\begin{align}
&\boldsymbol{Q}(\tilde{\boldsymbol{U}}) : 内力ベクトル \\
&\boldsymbol{f} : 等価節点力 \\
&\tilde{\boldsymbol{U}} : 全節点の変位をまとめたベクトル
\end{align}
ここで、$\boldsymbol{Q}(\tilde{\boldsymbol{U}})$、$\boldsymbol{f}$は下記のように表されます。
\boldsymbol{Q}(\tilde{\boldsymbol{U}}) = \sum_e \boldsymbol{q_e}(\tilde{\boldsymbol{u}}) \\
\boldsymbol{f} = \sum_e \boldsymbol{f_e} \\
\boldsymbol{q_e}(\tilde{\boldsymbol{u}}) = \boldsymbol{f_e} \\
\begin{align}
&\boldsymbol{q_e} : 要素内力ベクトル \\
&\boldsymbol{f_e} : 要素の等価節点力
\end{align}
また、$\boldsymbol{q_e}$は下記のように表されます。
\boldsymbol{q_e}(\tilde{\boldsymbol{u}}) = \int_v \boldsymbol{B}^T \sigma (\tilde{\boldsymbol{u}}) dV \\
\begin{align}
&\boldsymbol{B} : Bマトリクス \\
& \sigma : 要素内の応力
\end{align}
ニュートン・ラプソン法
残差力ベクトルを下記のように定義し、ニュートン・ラプソン法で残差力が$0$になる$\tilde{\boldsymbol{U}}$を求めます。
\boldsymbol{R}(\tilde{\boldsymbol{U}}) = \boldsymbol{Q}(\tilde{\boldsymbol{U}}) - \boldsymbol{f} \\
\boldsymbol{R} : 残差力ベクトル
収束演算は下記のように計算することができます。
\tilde{\boldsymbol{U}}_{i+1} = \tilde{\boldsymbol{U}}_{i} + \Delta \tilde{\boldsymbol{U}} \\
\Delta \tilde{\boldsymbol{U}} = - \boldsymbol{K_t}^{-1}(\tilde{\boldsymbol{U}}_{i}) \boldsymbol{R}(\tilde{\boldsymbol{U}}_{i}) \\
\boldsymbol{K_t}(\tilde{\boldsymbol{U}}_{i}) = \frac{\partial \boldsymbol{Q}}{\partial \tilde{\boldsymbol{U}}}(\tilde{\boldsymbol{U}}_{i}) \\
\quad \\
\boldsymbol{K_t} : 接線剛性マトリクス
また、接線剛性マトリクスは下記の式で求めることができます。
\boldsymbol{K_t}(\tilde{\boldsymbol{U}}_{i}) = \sum_e \boldsymbol{K_{et}}(\tilde{\boldsymbol{u}}_{i}) \\
\boldsymbol{K_{et}}(\tilde{\boldsymbol{u}}_{i}) = \frac{\partial \boldsymbol{q_e}}{\partial \tilde{\boldsymbol{u}}}(\tilde{\boldsymbol{u}}_{i}) \\
\boldsymbol{K_{et}} : 要素接線剛性マトリクス
ここで、トラス要素の要素接線剛性マトリクスは下記の式で表されます。
\boldsymbol{K_{et}} = \int_v \boldsymbol{B}^T D \boldsymbol{B} dV
\\
D = E \quad (弾性のとき) \\
D = H \quad (塑性のとき) \\
\begin{align}
E : ヤング率 \\
H : 接線係数
\end{align}
接線係数は下記の式で求めることができます。
H = \frac{EH'}{E + H'} \\
\begin{align}
& E &: ヤング率 \\
& H' &: 塑性係数 \\
\end{align}
要素接線剛性マトリクスのDはトラス要素のときのみ、上記の式で表せますが、
他の要素ではDマトリクスが整合接線係数という値によって表されます。
そのため、他の要素にそのまま使うことができないので、注意が必要です。
全体の処理の流れ
①. 荷重をインクリメント毎に分割する。(今回は等分割)
②. 変位$\tilde{\boldsymbol{U}}$を初期化する。
\tilde{\boldsymbol{U}} = \boldsymbol{0}
③. $i$インクリメントの残差力$\boldsymbol{R}$を初期化する。
\boldsymbol{R} = \boldsymbol{f}^{i} - \boldsymbol{f}^{i-1} \\
\boldsymbol{f}^i : iインクリメントの荷重
④. 接線剛性マトリクス$\boldsymbol{K_t}$を計算する。
\boldsymbol{K_t} = \sum_e \boldsymbol{K_{et}} \\
⑤. 接線剛性マトリクス$\boldsymbol{K_t}$と残差力$\boldsymbol{R}$に境界条件の処理を行う。
⑥. 変位の増分$\Delta \tilde{\boldsymbol{U}}$を求めて、変位$\tilde{\boldsymbol{U}}$を更新する。
\Delta \tilde{\boldsymbol{U}} = -\boldsymbol{K_t}^{-1} \boldsymbol{R}(\tilde{\boldsymbol{U}}_{i}) \\
\tilde{\boldsymbol{U}}_{j+1} = \tilde{\boldsymbol{U}}_j + \Delta \tilde{\boldsymbol{U}}
⑦. 要素のひずみを計算する。
\epsilon = \boldsymbol{B}\tilde{\boldsymbol{U}}
⑧. リターンマッピング法により、要素の塑性ひずみ$\epsilon_p$、応力$\sigma$を求める。
⑨. 内力ベクトルを計算する。
\boldsymbol{Q}= \sum_e \boldsymbol{q_e} \\
\boldsymbol{q_e} = \int_v \boldsymbol{B}^T \sigma dV
⑩. 残差力$\boldsymbol{R}$を計算する。
\boldsymbol{R} = \boldsymbol{Q} - \boldsymbol{f}^i
⑪. 収束判定を行う。
収束判定を満たしていなければ④に戻る。
⑫. インクリメントが最後の場合は処理を終了する。そうでなければ、$i = i+1$として③に戻る。

リターンマッピング法
線形硬化のリターンマッピング法
前回の投稿の内容をまとめます。
降伏関数
線形硬化の降伏関数は下記のように表されます。
f(\sigma, \epsilon_p) = |\sigma| - (\sigma_y + H'|\epsilon_p|) \\
\sigma_y : 降伏応力 \\
H' : 塑性係数
試行応力
試行応力$\sigma^{tri}_{i+1}$は下記のように定義されます。
\epsilon^{tri}_{i+1} = \epsilon_{i+1} - \epsilon_{p,i} \\
\sigma^{tri}_{i+1} = E \epsilon^{tri}_{i+1} \\
E : ヤング率
変形の判定
変形の判定は下記の式で行います。
f^{tri}_{i+1} = f(\sigma^{tri}_{i+1} ,\epsilon_{p, i}) = |\sigma^{tri}_{i+1}| - (\sigma_y + H'|\epsilon_{p,i}|) \\
ここで、$f^{tri}_{i+1} \leq 0$のときは弾性変形、$f^{tri}_{i+1} > 0$のときは塑性変形です。
応力、塑性ひずみの計算
$f^{tri}_{i+1} > 0$のとき、以下の式で応力と塑性ひずみを更新します。
\Delta \gamma = \frac{f^{tri}_{i+1}}{E + H'} \\
\sigma_{i+1} = \sigma^{tri}_{i+1} - E \Delta \gamma sign(\sigma^{tri}_{i+1}) \\
\epsilon_{p,i+1} = \epsilon_{p,i} + \Delta \gamma sign(\sigma^{tri}_{i+1})
また、$f^{tri}_{i+1} \leq 0$のときは、以下の式で応力と塑性ひずみを更新します。
\sigma_{i+1} = \sigma^{tri}_{i+1} \\
\epsilon_{p,i+1} = \epsilon_{p,i}
非線形硬化のリターンマッピング法
定式化
非線形硬化の場合、降伏関数が下記のように変化します。
f(\sigma, \epsilon_p) = |\sigma| - k(|\epsilon_p|) \\
k(|\epsilon_p|) : |\epsilon_p|における降伏応力 \\
そして、$f(\sigma_{i+1}, \epsilon_{p,i+1})$は下記のように表されます。
f(\sigma_{i+1}, \epsilon_{p,i+1}) = |\sigma_{i+1}| - k(|\epsilon_{p,i+1}|)
ここで、前回の投稿より以下の式が成り立ちます。
\left\{
\begin{array}{ll}
|\sigma_{i+1}| = |\sigma^{tri}_{i+1}| - E \Delta \gamma \\
|\epsilon_{p,i+1}| = |\epsilon_{p,i}| + \Delta \gamma \\
\end{array}
\right.
\\
\Delta \gamma = \dot{\gamma} \Delta t \\
\epsilon^{tri}_{i+1} = \epsilon_{i+1} - \epsilon_{p,i} \\
\sigma^{tri}_{i+1} = E \epsilon^{tri}_{i+1} \\
\dot{\gamma} : 塑性乗数(\dot{\gamma} \geq 0)
上の式を先ほどの降伏関数に代入すると下記のように表すことができます。
\begin{align}
f(\sigma_{i+1}, \epsilon_{p,i+1}) &= |\sigma_{i+1}| - k(|\epsilon_{p,i+1}|) \\
&= |\sigma^{tri}_{i+1}| - E \Delta \gamma - k(|\epsilon_{p,i}| + \Delta \gamma) \\
&= |\sigma^{tri}_{i+1}| - k(|\epsilon_{p,i}|) + k(|\epsilon_{p,i}|) - E \Delta \gamma - k(|\epsilon_{p,i}| + \Delta \gamma) \\
&= f^{tri}_{i+1} - E \Delta \gamma - k(|\epsilon_{p,i}| + \Delta \gamma) + k(|\epsilon_{p,i}|)
\end{align}
\\
ここで、$f^{tri}_{i+1}$は下記のように定義されます。
f^{tri}_{i+1} = f(\sigma^{tri}_{i+1} ,\epsilon_{p, i}) = |\sigma^{tri}_{i+1}| - k(|\epsilon_{p,i}|)
ここで、$f(\sigma_{i+1}, \epsilon_{p,i+1})$は$\Delta \gamma$に関する非線形方程式になります。そして、塑性変形するときは、$f(\sigma_{i+1}, \epsilon_{p,i+1})=0$となるので、それを満たす$\Delta \gamma$を見つける必要があります。
なお、塑性変形するかどうかは線形硬化のときと同じく$f^{tri}_{i+1}$が0より小さいか、大きいかで判断することで判断可能です。
$f(\sigma_{i+1}, \epsilon_{p,i+1})$は非線形方程式なので、ニュートン・ラプソン法で求めることができます。
ここで、ニュートン・ラプソン法では$f(x) = 0$となる解は下記のように収束演算で求めることができます。
x_0 = 0 \\
x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} \\
x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} \\
\vdots \\
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
$f(x_n) < tol(tol : 収束判定のパラメータ)$のとき、収束したとみなして、$x = x_n$とします。
これと全く同じ操作を行えば求めることが可能です。
f(\Delta \gamma) = f^{tri}_{i+1} - E \Delta \gamma - k(|\epsilon_{p,i}| + \Delta \gamma) + k(|\epsilon_{p,i}|) \\
f'(\Delta \gamma) = -E - \frac{\partial k}{\partial \Delta \gamma}(|\epsilon_{p,i}| + \Delta \gamma)
ここで、$\frac{\partial k}{\partial \Delta \gamma}$は下記の図のように応力-塑性ひずみ図の傾きの値になります。

今回は多直線で近似しているので、傾きの値は容易に取得することが可能です。
定式化は以上になります。最後に処理をまとめてみます。
① 試行応力$\sigma_{i+1}^{tri}$を計算する
\sigma^{tri}_{i+1} = E (\epsilon_{i+1} - \epsilon_{p,i})
② $f^{tri}_{i+1}$を計算する
f^{tri}_{i+1} = f(\sigma^{tri}_{i+1} ,\epsilon_{p, i}) = |\sigma^{tri}_{i+1}| - k(|\epsilon_{p,i}|) \\
③ $f^{tri}_{i+1} \leq 0$ならば$\Delta \gamma = 0$、$f^{tri}_{i+1} > 0$ならばニュートン・ラプソン法で下記の式を満たす$\Delta \gamma$を計算する
f(\Delta \gamma) = f^{tri}_{i+1} - E \Delta \gamma - k(|\epsilon_{p,i}| + \Delta \gamma) + k(|\epsilon_{p,i}|) = 0
④塑性ひずみ$\epsilon_{p, i+1}$と応力$\sigma_{i+1}$を計算する
\sigma_{i+1} = \sigma^{tri}_{i+1} - E \Delta \gamma sign(\sigma^{tri}_{i+1}) \\
\epsilon_{p,i+1} = \epsilon_{p,i} + \Delta \gamma sign(\sigma^{tri}_{i+1})
Pythonで実装する
この処理をmaterialクラスとしてPythonで実装してみます。
ここで、塑性係数$H'$を求めるために弾塑性の材料情報を入力する必要がありますが、Abaqusの仕様にならって、データを下記の図のように入力します。

入力ポイントの追加はaddStressPStrainLine関数で実装しています。
returnMapping法の処理はreturnMapping関数で行っています。
他はreturnMapping関数で使うための関数です。
material.py
import numpy as np
# 材料情報を格納するクラス
class Material:
# コンストラクタ
# young : ヤング率
# area : 面積
def __init__(self, young, area):
# インスタンス変数を定義する
self.young = young # ヤング率
self.area = area # 面積
self.stressLine = [] # 応力-塑性ひずみ多直線の応力データ
self.pStrainLine = [] # 応力-塑性ひずみ多直線の塑性ひずみデータ
self.itrNum = 100 # ニュートン・ラプソン法の収束回数の上限
self.tol = 0.001 # ニュートン・ラプソン法の収束基準
# 応力-塑性ひずみ多直線のデータを追加する
# (入力されるデータは塑性ひずみが小さい順になり、最初の塑性ひずみは0.0にならなければいけない)
# (塑性係数は正になる前提)
# stress : 応力(正の前提)
# pStrain : 塑性ひずみ(正の前提)
def addStressPStrainLine(self, stress, pStrain):
# 入力チェック
if len(self.pStrainLine) == 0:
if not pStrain == 0.0 :
raise ValueError("応力-塑性ひずみ多直線データの最初のひずみは0.0になる必要があります。")
elif self.pStrainLine[-1] > pStrain:
raise ValueError("応力-塑性ひずみ多直線データの入力順序が間違っています。")
# 最初の入力の場合は降伏応力を格納する
if len(self.stressLine) == 0:
self.yieldStress = stress # 降伏応力
self.stressLine.append(stress)
self.pStrainLine.append(pStrain)
# 降伏関数を計算する
# (0より大きければ降伏している)
# stress : 応力
# pStrain : 塑性ひずみ
def yieldFunction(self, stress, pStrain):
f = 0.0
if hasattr(self, 'yieldStress'):
f = np.abs(stress) - self.makeYeildStress(pStrain)
return f
# 降伏応力を求める
# pStrain : 塑性ひずみ
def makeYeildStress(self, pStrain):
yeildStress = 0.0
if hasattr(self, 'yieldStress'):
# pStrainが何番目のデータの間か求める
no = None
for i in range(len(self.pStrainLine) - 1):
if self.pStrainLine[i] <= np.abs(pStrain) and np.abs(pStrain) <= self.pStrainLine[i+1]:
no = i
break
if no is None :
raise ValueError("塑性ひずみが定義した範囲を超えています。")
hDash = self.makePlasticModule(pStrain)
yeildStress = hDash * (np.abs(pStrain) - self.pStrainLine[no]) + self.stressLine[no]
return yeildStress
# 塑性係数を求める
# pStrain : 塑性ひずみ
def makePlasticModule(self, pStrain):
# pStrainが何番目のデータの間か求める
no = None
for i in range(len(self.pStrainLine) - 1):
if self.pStrainLine[i] <= np.abs(pStrain) and np.abs(pStrain) <= self.pStrainLine[i+1]:
no = i
break
if no is None :
raise ValueError("塑性ひずみが定義した範囲を超えています。")
# 塑性係数を計算する
h = (self.stressLine[no+1] - self.stressLine[no]) / (self.pStrainLine[no+1] - self.pStrainLine[no])
return h
# Return Mapping法により、ひずみ増分、降伏判定を更新する
# strain : 全ひずみ
# prevPStrain : 前回の塑性ひずみ
def returnMapping(self, strain, prevPStrain):
# 試行弾性応力を求める
triStrain = strain - prevPStrain
triStress = self.young * triStrain
# 降伏関数を計算する
triF = self.yieldFunction(triStress, np.abs(prevPStrain))
# 降伏判定を計算する
if triF > 0.0 :
yeildFlg = True
else:
yeildFlg = False
# 塑性ひずみの増分量をニュートン・ラプソン法で計算する
deltaGamma = 0.0
if triF > 0.0 :
kn = self.makeYeildStress(prevPStrain)
# 収束演算を行う
for i in range(self.itrNum):
# y, y'を計算する
k = self.makeYeildStress(prevPStrain + deltaGamma)
hDash = self.makePlasticModule(prevPStrain + deltaGamma)
y = triF - self.young * deltaGamma - k + kn
yDash = - self.young - hDash
# 収束判定を行う
if np.abs(y) < self.tol:
break
deltaGamma -= y / yDash
deltaPStrain = deltaGamma * np.sign(triStress)
# 塑性ひずみを計算する
pStrain = prevPStrain + deltaPStrain
# 応力を計算する
stress = triStress - self.young * deltaPStrain
return stress, pStrain, yeildFlg
トラス要素(弾塑性)
ここでは、トラス要素の要素接線剛性マトリクス$\boldsymbol{K_{et}}$と要素内力ベクトル$\boldsymbol{q_e}$を求める処理を実装します。
要素内力ベクトル
要素内力ベクトル$\boldsymbol{q_e}$は下記の式で表すことができました。
\boldsymbol{q_e} = \int_v \boldsymbol{B}^T \sigma dV \\
上の式の$\sigma$はリターンマッピング法により求めることが可能です。
ただ、$\boldsymbol{q_e}$はこのままでは積分が入っていて少し求めるのが面倒です。
そこで、要素内力ベクトル$\boldsymbol{q_e}$を正規座標系$a$に変数変換してガウス求積を使って求めます。
\begin{align}
\boldsymbol{q_e} &= \int_v \boldsymbol{B}^T \sigma dV \\
&= A \int \boldsymbol{B}^T \sigma dx \\
&= A \int_{-1}^{1} \boldsymbol{B}^T \sigma \frac{dx}{da} da \\
&= A w \boldsymbol{B}^T \sigma \frac{dx}{da}
\end{align}
\\
\boldsymbol{B} =
\begin{bmatrix}
-\frac{1}{-x_1 + x_2} && \frac{1}{-x_1 + x_2} \\
\end{bmatrix}
\\
\frac{d x}{d a} = \frac{1}{2}(-x_1 + x_2)
\\
x_i : i節点のx座標値 \\
A : 断面積 \\
w = 2.0 : 重み係数
$\boldsymbol{B}$マトリクスの導出、正規座標系についてはこちらの記事を参照ください。
要素接線剛性マトリクス
トラス要素の接線剛性マトリクスは上述の通り、下記の式で表されます。
\begin{align}
\boldsymbol{K_{et}} = \int_v \boldsymbol{B}^T D \boldsymbol{B} dv
\end{align}
\\
D = E \quad (弾性のとき) \\
D = H \quad (塑性のとき)
ここで、トラス要素の節点を正規座標系$a$に変数変換してガウス求積を使うと、下記のように求めることができます。
\begin{align}
\boldsymbol{K_{et}} &= \int_v \boldsymbol{B}^T D \boldsymbol{B} dv \\
&= A \int \boldsymbol{B}^TD\boldsymbol{B} dx \\
&= A \int_{-1}^{1} \boldsymbol{B}^TD\boldsymbol{B} \frac{d x}{d a} da \\
&= Aw \boldsymbol{B}^T D\boldsymbol{B} \frac{d x}{d a}
\end{align}
\\
A : 断面積 \\
w = 2.0 : 重み係数
Pythonで実装する
トラス要素の計算を行うクラスd1t2を実装します。
また、d1t2クラスを実装するためにNode1dクラスを実装します。
Node1dクラスは節点情報を格納するだけのクラスです。
Node1d.py
class Node1d:
# コンストラクタ
# no : 節点番号
# x : x座標
# y : y座標
def __init__(self, no, x):
self.no = no # 節点番号
self.x = x # x座標
# 節点の情報を表示する
def printNode(self):
print("Node No: %d, x: %f" % (self.no, self.x))
d1t2クラスはコンストラクタの引数で先ほど実装したmaterialクラスを引数にとります。
d1t2クラスのmakeKetmatrix関数で要素接線剛性マトリクスを計算します。
また、makeqVector関数で内力ベクトルを計算します。
returnMapping関数は変位が更新されたときにリターンマッピング法により、応力、ひずみを計算するための関数です。
d1t2.py
import numpy as np
# 1次元2節点トラス要素のクラス
class d1t2:
# コンストラクタ
# no : 要素番号
# nodes : 節点のリスト(Node1d型のリスト)
# material : 材料特性(Material型)
def __init__(self, no, nodes, material):
# インスタンス変数を定義する
self.no = no # 要素番号
self.nodes = nodes # 節点のリスト(Node1d型のリスト形式)
self.mat = material # 材料データ(Material型)
self.area = material.area # 断面積
self.young = material.young # ヤング率
self.ipNum = 1 # 積分点の数
self.w = 2.0 # 積分点の重み係数
self.yeildFlg = False # 要素が降伏しているか判定するフラグ
self.pStrain = 0.0 # 要素内の塑性ひずみ
self.stress = 0.0 # 要素内の応力
# Bマトリクスを計算する
self.matB = self.makeBmatrix()
# 要素接線剛性マトリクスKetを作成する
def makeKetmatrix(self):
# dxdaを計算する
dxda = -0.5 * self.nodes[0].x + 0.5 * self.nodes[1].x
# 降伏状態を判定し、Dを作成する
if self.yeildFlg == False:
D = self.young
else:
hDash = self.mat.makePlasticModule(self.pStrain)
D = self.young * hDash / (self.young + hDash)
# 要素接線剛性マトリクスKetを計算する
matKet = self.area * self.w * self.matB.T * D * self.matB * dxda
return matKet
# Bマトリクスを作成する
def makeBmatrix(self):
# Bマトリクスを計算する
dN1dx = -1 / (-self.nodes[0].x + self.nodes[1].x)
dN2dx = 1 / (-self.nodes[0].x + self.nodes[1].x)
matB = np.matrix([[dN1dx, dN2dx]])
return matB
# Return Mapping法により、応力、塑性ひずみ、降伏判定を更新する
# vecElemDisp : 要素節点の変位ベクトル(np.array型)
def returnMapping(self, vecElemDisp):
# 全ひずみを求める
strain = np.array(self.matB @ vecElemDisp).flatten()
# リターンマッピング法により、応力、塑性ひずみ、降伏判定を求める
stress, pStrain, yieldFlg = self.mat.returnMapping(strain, self.pStrain)
self.stress = stress
self.pStrain = pStrain
self.yeildFlg = yieldFlg
# 内力ベクトルqを作成する
def makeqVector(self):
# dxdaを計算する
dxda = -0.5 * self.nodes[0].x + 0.5 * self.nodes[1].x
# 内力ベクトルqを計算する
vecq = np.array(self.area * self.w * self.matB.T @ self.stress * dxda).flatten()
return vecq
接線剛性マトリクス
接線剛性マトリクス$\boldsymbol{K_t}$は1次元の場合、全節点数を$N$とすると下記のように表されます。
\boldsymbol{K_t}=
\begin{bmatrix}
K_{11} && K_{12} && \cdots && K_{1, N} \\
K_{21} && K_{22} && \cdots && K_{2, N} \\
\vdots && \vdots && \ddots && \vdots \\
K_{N, 1} && K_{N, 2} && \cdots && K_{N, N}
\end{bmatrix}
上記のように、$N×N$の行列になります。ここで、トラス要素の要素接線剛性マトリクスは節点数2個なので$2×2$の行列になります。そのため、接線剛性マトリクスに足し合わせるために対応する行列の位置を求める必要があります。
トラス要素の節点番号を$i$, $j$とすると、接線剛性マトリクスに格納する位置は下記のように表すことができます。
\boldsymbol{K_{et}}=
\begin{bmatrix}
K_{i, i} && K_{i, j} \\
K_{i, j} && K_{j, j} \\
\end{bmatrix}
境界条件の処理
$\boldsymbol{K_t}$を使って$\Delta \tilde{\boldsymbol{U}}$の計算をする前に境界条件の処理をする必要があります。
今回は$\boldsymbol{K_t} \Delta \tilde{\boldsymbol{U}}= \boldsymbol{R}$に単点拘束の境界条件を考慮した処理を行います。
単点拘束とは一つの節点自由度で構成される拘束のことで、例えば$u_1 = 0(u_1: 節点1の変位)$などの拘束を言います。
ここで、例として、接線剛性マトリクスが$3×3$で既知量$u_2 = \bar{u}$の場合で考えます。
すると、下記のように表すことができます。
\begin{bmatrix}
K_{11} && K_{12} && K_{13} \\
K_{21} && K_{22} && K_{23} \\
K_{31} && K_{32} && K_{33} \\
\end{bmatrix}
\begin{bmatrix}
u_1 \\
\bar{u} \\
u_3 \\
\end{bmatrix}
=
\begin{bmatrix}
r_1 \\
r_2 \\
r_3 \\
\end{bmatrix}
\\
K_{11} u_1 + K_{12} \bar{u} + K_{13} u_3 = r_1 \\
K_{21} u_1 + K_{22} \bar{u} + K_{23} u_3 = r_2 \\
K_{31} u_1 + K_{32} \bar{u} + K_{33} u_3 = r_3 \\
既知量を右に移動すると
K_{11} u_1 + K_{13} u_3 = r_1 - K_{12} \bar{u} \\
K_{21} u_1 + K_{23} u_3 = r_2 - K_{22} \bar{u} \\
K_{31} u_1 + K_{33} u_3 = r_3 - K_{32} \bar{u}
となり、真ん中の式を省いて代わりに、$u_2 = \bar{u}$を代入すると、
K_{11} u_1 + K_{13} u_3 = r_1 - K_{12} \bar{u} \\
u_2 = \bar{u} \\
K_{31} u_1 + K_{33} u_3 = r_3 - K_{32} \bar{u} \\
\begin{bmatrix}
K_{11} && 0 && K_{13} \\
0 && 1 && 0 \\
K_{31} && 0 && K_{33}
\end{bmatrix}
\begin{bmatrix}
u_1 \\
\bar{u} \\
u_3
\end{bmatrix}
=
\begin{bmatrix}
r_1 \\
\bar{u} \\
r_3
\end{bmatrix}
-
\begin{bmatrix}
K_{12} \\
0 \\
K_{32}
\end{bmatrix}
\bar{u} \
とすることができます。ここで、式を一つ省くことを行っていますが、一般に節点が拘束されている点の荷重値(反力)は未知数なので、未知の値$f_2$を行列から消して変位を求めることが可能となります。
このような処理をすることで、$\boldsymbol{K_t} \Delta \tilde{\boldsymbol{U}}= \boldsymbol{R}$の式を解くことが可能となります。
ここで境界条件を格納するクラスとしてBoundary1dクラスを実装します。(境界条件の処理を行うクラスは後に実装します。)
基本的には境界条件を格納するだけのクラスです。
addSPC関数で単点拘束を追加、addForce関数で荷重を追加します。makeDispVector関数、makeForceVector関数は設定した拘束条件をベクトルの形で返します。
Boundary1d.py
import numpy as np
class Boundary1d:
# コンストラクタ
# nodeNum : 節点数
def __init__(self, nodeNum):
# インスタンス変数を定義する
self.nodeNum = nodeNum # 全節点数
self.dispNodeNo = [] # 単点拘束の節点番号
self.dispX = [] # 単点拘束の強制変位x
self.forceNodeNo = [] # 荷重が作用する節点番号
self.forceX = [] # x方向の荷重
self.matC = np.empty((0, self.nodeNum)) # 多点拘束用のCマトリクス
self.vecd = np.empty(0) # 多点拘束用のdベクトル
# 単点拘束を追加する
# nodeNo : 節点番号
# x : 強制変位量
def addSPC(self, nodeNo, x):
self.dispNodeNo.append(nodeNo)
self.dispX.append(x)
# 単点拘束条件から変位ベクトルを作成する
def makeDispVector(self):
vecd = np.array([None] * self.nodeNum)
for i in range(len(self.dispNodeNo)):
vecd[(self.dispNodeNo[i] - 1)] = self.dispX[i]
return vecd
# 荷重を追加する
# nodeNo : 節点番号
# fx : 荷重値
def addForce(self, nodeNo, fx):
self.forceNodeNo.append(nodeNo)
self.forceX.append(fx)
# 境界条件から荷重ベクトルを作成する
def makeForceVector(self):
vecf = np.array(np.zeros([self.nodeNum]))
for i in range(len(self.forceNodeNo)):
vecf[(self.forceNodeNo[i] - 1)] += self.forceX[i]
return vecf
# 拘束条件を出力する
def printBoundary(self):
print("Node Number: ", self.nodeNum)
print("SPC Constraint Condition")
for i in range(len(self.dispNodeNo)):
print("Node No: " + str(self.dispNodeNo[i]) + ", x: " + str(self.dispX[i]))
print("Force Condition")
for i in range(len(self.forceNodeNo)):
print("Node No: " + str(self.forceNodeNo[i]) + ", x: " + str(self.forceX[i]))
有限要素法を解く処理を実装する
上記で実装したクラスを使って解析を行うFEM1dクラスを実装します。
FEM1dクラスはimpAnalysis関数で陰解法の解析を行います。
また、outputTxt関数で解析結果をテキスト形式で出力することができます。
他の関数は上記の関数を計算するための関数です。
FEM1d.py
import numpy as np
import numpy.linalg as LA
from Boundary1d import Boundary1d
class FEM1d:
# コンストラクタ
# nodes : 節点リスト(節点は1から始まる順番で並んでいる前提(Node1d型のリスト))
# elements : 要素のリスト(d1t2型のリスト)
# boundary : 境界条件(d1Boundary型)
# incNum : インクリメント数
def __init__(self, nodes, elements, boundary, incNum):
self.nodes = nodes # 節点は1から始まる順番で並んでいる前提(Node1d型のリスト)
self.elements = elements # 要素のリスト(d1t2型のリスト)
self.bound = boundary # 境界条件(d1Boundary型)
self.incNum = incNum # インクリメント数
self.itrNum = 100 # ニュートン法のイテレータの上限
self.cn = 0.001 # ニュートン法の変位の収束判定のパラメータ
# 陰解法で解析を行う
def impAnalysis(self):
self.vecDispList = [] # インクリメント毎の変位ベクトルのリスト(np.array型のリスト)
self.vecRFList = [] # インクリメント毎の反力ベクトルのリスト(np.array型のリスト)
self.elemOutputDataList = [] # インクリメント毎の要素出力のリスト(makeOutputData型のリストのリスト)
# 荷重をインクリメント毎に分割する
vecfList = []
for i in range(self.incNum):
vecfList.append(self.makeForceVector() * (i + 1) / self.incNum)
# ニュートン法により変位を求める
vecDisp = np.zeros(len(self.nodes)) # 全節点の変位ベクトル
vecR = np.zeros(len(self.nodes)) # 残差力ベクトル
for i in range(self.incNum):
vecDispFirst = vecDisp # 初期の全節点の変位ベクトル
vecf = vecfList[i] # i+1番インクリメントの荷重
# 境界条件を考慮しないインクリメント初期の接線剛性マトリクスKtを作成する
matKt = self.makeKtmatrix()
# 境界条件を考慮しないインクリメント初期の残差力ベクトルRを作成する
if i == 0:
vecR = vecfList[0]
else:
vecR = vecfList[i] - vecfList[i - 1]
# 境界条件を考慮したインクリメント初期の接線剛性マトリクスKtc、残差力ベクトルRcを作成する
matKtc, vecRc = self.setBoundCondition(matKt, vecR)
# 収束演算を行う
for j in range(self.itrNum):
# Ktcの逆行列が計算できるかチェックする
if np.isclose(LA.det(matKtc), 0.0) :
raise ValueError("有限要素法の計算に失敗しました。")
# 変位ベクトルを計算する
vecd = LA.solve(matKtc, vecRc)
vecDisp += vecd
# 要素内の塑性ひずみ、応力を更新する
self.returnMapping(vecDisp)
# 新たな残差力ベクトルRを求める
vecQ = np.zeros(len(self.nodes))
for elem in self.elements:
vecq = elem.makeqVector()
for k in range(len(elem.nodes)):
vecQ[(elem.nodes[k].no - 1)] += vecq[k]
vecR = vecf - vecQ
# 新たな接線剛性マトリクスKtを作成する
matKt = self.makeKtmatrix()
# 新たな境界条件を考慮したKtcマトリクス、Rcベクトルを作成する
matKtc, vecRc = self.setBoundCondition(matKt, vecR)
# 収束判定を行う
if np.isclose(LA.norm(vecd), 0.0):
break
dispRate = (LA.norm(vecd) / LA.norm(vecDisp - vecDispFirst))
if dispRate < self.cn:
break
# インクリメントの最終的な変位べクトルを格納する
self.vecDispList.append(vecDisp.copy())
# 節点反力を計算する
vecRF = np.array(vecQ - vecf).flatten()
# インクリメントの最終的な節点反力を格納する
self.vecRFList.append(vecRF)
# ReturnMapping法により、要素内の応力、塑性ひずみ、降伏判定を更新する
# vecDisp : 全節点の変位ベクトル(np.array型)
def returnMapping(self, vecDisp):
for elem in self.elements:
vecElemDisp = np.zeros(len(elem.nodes))
for i in range(len(elem.nodes)):
vecElemDisp[i] = vecDisp[(elem.nodes[i].no - 1)]
elem.returnMapping(vecElemDisp)
# 接線剛性マトリクスKtを作成する
def makeKtmatrix(self):
matKt = np.matrix(np.zeros((len(self.nodes), len(self.nodes))))
for elem in self.elements:
# ketマトリクスを計算する
matKet = elem.makeKetmatrix()
# Ktマトリクスに代入する
for c in range(len(elem.nodes)):
ct = (elem.nodes[c].no - 1)
for r in range(len(elem.nodes)):
rt = (elem.nodes[r].no - 1)
matKt[ct, rt] += matKet[c, r]
return matKt
# 節点に負荷する荷重、等価節点力を考慮した荷重ベクトルを作成する
def makeForceVector(self):
# 節点に負荷する荷重ベクトルを作成する
vecf = self.bound.makeForceVector()
return vecf
# 接線剛性マトリクス、残差力ベクトルに境界条件を考慮する
def setBoundCondition(self, matKt, vecR):
matKtc = np.copy(matKt)
vecRc = np.copy(vecR)
# 単点拘束条件を考慮した接線剛性マトリクス、残差力ベクトルを作成する
vecDisp = self.bound.makeDispVector()
for i in range(len(vecDisp)):
if not vecDisp[i] == None:
# Ktマトリクスからi列を抽出する
vecx = np.array(matKt[:, i]).flatten()
# 変位ベクトルi列の影響を荷重ベクトルに適用する
vecRc = vecRc - vecDisp[i] * vecx
# Ktマトリクスのi行、i列を全て0にし、i行i列の値を1にする
matKtc[:, i] = 0.0
matKtc[i, :] = 0.0
matKtc[i, i] = 1.0
for i in range(len(vecDisp)):
if not vecDisp[i] == None:
vecRc[i] = vecDisp[i]
return matKtc, vecRc
# 解析結果をテキストファイルに出力する
def outputTxt(self, filePath):
# ファイルを作成し、開く
f = open(filePath + ".txt", 'w')
# 出力する文字の情報を定義する
columNum = 20
floatDigits = ".10g"
# 入力データのタイトルを書きこむ
f.write("*********************************\n")
f.write("* Input Data *\n")
f.write("*********************************\n")
f.write("\n")
# 節点情報を出力する
f.write("***** Node Data ******\n")
f.write("No".rjust(columNum) + "X".rjust(columNum) + "\n")
f.write("-" * columNum * 2 + "\n")
for node in self.nodes:
strNo = str(node.no).rjust(columNum)
strX = str(format(node.x, floatDigits).rjust(columNum))
f.write(strNo + strX + "\n")
f.write("\n")
# 要素情報を出力する
nodeNoColumNum = columNum
f.write("***** Element Data ******\n")
f.write("No".rjust(columNum) + "Type".rjust(columNum) + "Node No".rjust(nodeNoColumNum) +
"Young".rjust(columNum) + "Area".rjust(columNum) + "\n")
f.write("-" * columNum * 4 + "-" * nodeNoColumNum + "\n")
for elem in self.elements:
strNo = str(elem.no).rjust(columNum)
strType = str(elem.__class__.__name__ ).rjust(columNum)
strNodeNo = ""
for node in elem.nodes:
strNodeNo += " " + str(node.no)
strNodeNo = strNodeNo.rjust(nodeNoColumNum)
strYoung = str(format(elem.young, floatDigits).rjust(columNum))
strArea = str(format(elem.area, floatDigits).rjust(columNum))
f.write(strNo + strType + strNodeNo + strYoung + strArea + "\n")
f.write("\n")
# 単点拘束情報を出力する
f.write("***** SPC Constraint Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Displacement".rjust(columNum) + "\n")
f.write("-" * columNum * 2 + "\n")
for i in range(len(self.bound.dispNodeNo)):
strNo = str(self.bound.dispNodeNo[i]).rjust(columNum)
strXDisp = "None".rjust(columNum)
if not self.bound.dispX[i] is None:
strXDisp = str(format(self.bound.dispX[i], floatDigits).rjust(columNum))
f.write(strNo + strXDisp + "\n")
f.write("\n")
# 荷重条件を出力する(等価節点力も含む)
f.write("***** Nodal Force Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Force".rjust(columNum) + "\n")
f.write("-" * columNum * 2 + "\n")
vecf = self.makeForceVector()
for i in range(len(self.nodes)):
if not vecf[i] == 0 :
strNo = str(i + 1).rjust(columNum)
strXForce = str(format(vecf[i], floatDigits).rjust(columNum))
f.write(strNo + strXForce + "\n")
f.write("\n")
# 結果データのタイトルを書きこむ
f.write("**********************************\n")
f.write("* Result Data *\n")
f.write("**********************************\n")
f.write("\n")
for i in range(self.incNum):
f.write("*Increment " + str(i + 1) + "\n")
f.write("\n")
# 変位のデータを出力する
f.write("***** Displacement Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Displacement".rjust(columNum) + "\n")
f.write("-" * columNum * 2 + "\n")
for j in range(len(self.nodes)):
strNo = str(j + 1).rjust(columNum)
vecDisp = self.vecDispList[i]
strXDisp = str(format(vecDisp[j], floatDigits).rjust(columNum))
f.write(strNo + strXDisp + "\n")
f.write("\n")
# 反力のデータを出力する
f.write("***** Reaction Force Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Force".rjust(columNum) + "\n")
f.write("-" * columNum * 2 + "\n")
for j in range(len(self.nodes)):
strNo = str(j + 1).rjust(columNum)
vecRF = self.vecRFList[i]
strXForce = str(format(vecRF[j], floatDigits).rjust(columNum))
f.write(strNo + strXForce + "\n")
f.write("\n")
# ファイルを閉じる
f.close()
例題を解く
上記より、ようやくクラスの準備ができたので、下記の例題を解いてみます。
メインの処理
上記の例題を計算するためにメイン処理を行うmain.pyを実装します。
main.pyはこれまでに実装したクラスを使って例題を解き、結果を"test.txt"ファイルに出力します。
また、インクリメントは10分割にします。
main.py
from Node1d import Node1d
from Material import Material
from Boundary1d import Boundary1d
from FEM1d import FEM1d
from d1t2 import d1t2
# メインの処理
def main():
# 節点を定義する
node1 = Node1d(1, 0.0)
node2 = Node1d(2, 100.0)
nodes = [node1, node2]
nodes1 = [node1, node2]
# 材料情報を定義する
area = 1.0
young = 210e3
mat = Material(young, area)
mat.addStressPStrainLine(200e3, 0.0)
mat.addStressPStrainLine(250e3, 0.2)
mat.addStressPStrainLine(290e3, 0.4)
mat.addStressPStrainLine(320e3, 0.6)
mat.addStressPStrainLine(340e3, 0.8)
mat.addStressPStrainLine(350e3, 1.0)
# 要素を定義する
elem1 = d1t2(1, nodes1, mat)
elems = [elem1]
# 境界条件を定義する
bound = Boundary1d(len(nodes))
bound.addSPC(1, 0.0)
bound.addForce(2, 345e3)
# 解析を行う
fem = FEM1d(nodes, elems, bound, 10)
fem.impAnalysis()
fem.outputTxt("test")
main()
Abaqus Student Edition2021と比較する
いつも通り、上記の計算結果があっているか、Abaqusを使って検証してみます。
Abaqusの入力ファイル
*node
1, 0.0
2, 100.0
*element, type=t2d2, elset=elems
1, 1, 2
*material, name=mat
*elastic
210e3
*plastic
200e3, 0.0
250e3, 0.2
290e3, 0.4
320e3, 0.6
340e3, 0.8
350e3, 1.0
*solid section, elset=elems, material=mat
1.0
*boundary
1, 1, 3
*step
*static, direct
0.1, 1.0
*cload
2, 1, 345e3
*end step
結果を比較してみます。
数値計算の誤差レベルで一致することが確認できました。
余談
上記の例題ではAbaqusと結果が一致しますが、下記のような材料特性だと結果が異なります。
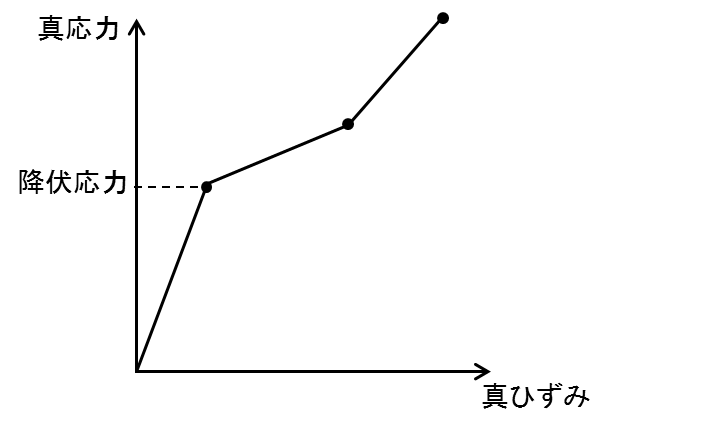
このような材料が存在するかは分かりませんが、この材料を入力すると、ニュートン・ラプソン法の収束過程で残差力が荷重とは反対方向になるイテレーションが存在します。
ただその残差力は塑性変形するほど大きい値でないためにリターンマッピング法の過程で塑性変形とは見なされず、弾性変形と仮定して解きます。
しかし、Abaqusでは同じインクリメントで一度塑性変形した場合は、後のイテレーションでも残差力の大きさに関わらず塑性変形とみなして計算する?ような処理が組み込まれているようです。
そのため、異なった結果が出力されます。
ただ、Abaqusの内部処理が本当にそうなっているのか自信がないため、今回はあえてその処理を実装しないことにしました。
同様の問題を扱っている論文があったので、興味がある方は参照してみてください。
弾性予測子/リターンマッピングによる拡張下負荷面モデルの応力計算における負荷判定法の改良
Abaqusの処理をトレースしたところ、要素内のひずみ(塑性ひずみ、相当塑性ひずみ)の更新はインクリメントが変化するタイミングで行われるようです。
本稿で実装している方法ではイテレーションが更新するタイミングで要素内のひずみを更新しているため結果に差が生じるようです。
そのため、要素内のひずみがインクリメントが変化するタイミングにプログラムを修正することで結果が一致します。





