LoginSignup
240
201

More than 3 years have passed since last update.

@7shi

モナド則がちょっと分かった？

Last updated at Posted at 2014-12-01

モナドを勉強しようとするとモナド則が立ちはだかります。しかしモナド則は意味だけでなく、それがモナドを勉強する上でどういう位置付けなのかも分かりにくいです。とりあえず棚上げしたまま分かる範囲のことから手を付けていましたが、ちょっと分かったような気がしたのでメモしておきます。

  • モナド則に関する現時点の理解ですが、正確さは保証できません。
  • これを読めばモナドが理解できるという類の説明（モナドチュートリアル）ではありません。
  • 試験的にモナド則を図示しました。コードを図に転写して、多少の解釈を加えたものです。もし分かりにくければ無視しても構いません。

この記事はHaskell 超入門シリーズの番外編です。

モナド則

モナド則は return と >>= の動きに関するルールです。

  1. return x >>= f == f x
  2. m >>= return == m
  3. (m >>= f) >>= g == m >>= (\x -> f x >>= g)

各モナド則は式を == で区切り、左辺と右辺が等しいかを見ます。等しくなるものがモナドだ、というルールです。等しくならないものは作れますが、それはモナドではありません。

解釈を書いておきます。（詳細は後述）

  1. >>= の左側の return が消せることを要請します。
  2. >>= の右側の return が消せることを要請します。
  3. あらかじめ関数が合成できることを要請します。

※ 余談ですが、いきなりこういうのを見せられたときの感覚が、次のツイートでうまく表現されていると思いました。

何でないか

  • モナドを勉強するには、まずモナド則を理解しないといけないわけではありません。
  • モナド則を理解すれば、モナドがすっきり分かるというものではありません。

何であるか

  • モナド則は、モナドを作るときに守らないといけないルールです。
  • モナドを使う側の立場からは、コードを整理するのに役立ちそうです。

モナドの勉強

モナドをどう勉強するかについて、現段階で感じていることです。

  • モナドの勉強にあたって、モナドの作り方から入るのは難しいです。オブジェクト指向を勉強するときに、クラスの作り方から入るようなものです。（それは難しいよね、という意味合いです）
  • モナドが何かという抽象的な問いかけはしなくても、単なるプログラミングテクニックとして既存のモナドは使えそうです。オブジェクト指向で例えれば、デザインパターンに沿ってきれいな設計のクラスが作れなくても、既存のクラスは使えるようなものです。

※ もちろん最終的にはモナドが作れるに越したことはありませんが、ここで想定しているのは学習の初期段階です。

次のような見解もあります。

モナド・ミニマム

returnと>>=で操作できてモナド則を満たすものをモナドと呼びます。

モナドはよく箱だと言われます。中に値が入った箱です。

Monad.png

リストの実体もモナドで、まさに値が入った箱です（例：[1]）。そのためモナド代表としてリストで説明します。

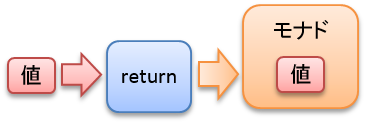
return

returnはモナドという箱に値を入れるための関数です。

return.png

ghciで確認します。

Prelude> return 1
1

これだけでは単なる1と区別が付かないので、:tで型を調べます。

Prelude> :t 1
1 :: Num a => a
Prelude> :t return 1
return 1 :: (Monad m, Num a) => m a

単なる1と、モナドに入れられた1とは型が異なることが確認できました。

※ 一番下の行の => の右側の m a に注目してください。

型表記を単純にするため、1がIntであることを指定します。

Prelude> :t return (1 :: Int)
return (1 :: Int) :: Monad m => m Int

※ m a が　m Int に変化したことに注目してください。

モナドの型を指定します。リスト型は[]です。

Prelude> return 1 :: [] Int
[1]

※ m Int の m を [] に置き換えて [] Int となります。[Int] とも書けます。

型を指定することで、returnによりリストモナドに1という値を入れることができました。複雑な書き方をしていますが、得られるものは[1]と同じです。

>>=

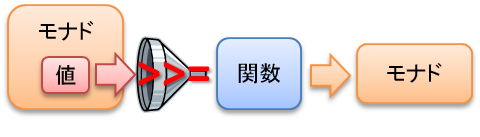
モナドを関数に渡すための演算子が>>=（バインドと読む）です。

モナド >>= 関数で以下の処理が行われます。（漏斗に例えています）

bind.png

  1. モナドから値が取り出されます。
  2. 取り出された値が関数に引数として渡されます。
  3. 関数では戻り値をモナドに入れて返します。

関数はモナドを返す必要があります。一番簡単な対応方法は計算結果をreturnでモナドに入れることです。

Prelude> let f x = return $ x + 1

動作を確認します。

Prelude> [1] >>= f
[2]

モナドから1が取り出されて関数fに渡され、関数の戻り値が表示されました。

連続

わざわざ>>=などというものを用意して、しかもモナドから値の出し入れなどという複雑なことをしているのは、それを連続させたいからのようです。

Prelude> [1] >>= f >>= f >>= f >>= f
[5]

これで何が嬉しいのかは、具体的に意味のあるものを作ってみないと実感しにくいです。しかし簡単なサンプルは思い付かないので、別の言語で似た例を示します。

メソッドチェイン

>>=を連続させる使い方は、オブジェクト指向言語におけるメソッドチェインに似ています。

  • x >>= f >>= f >>= f >>= f
  • x.f().f().f().f()

C#での実装例を示します。オブジェクト指向でモナドを模倣すると冗長になります。

C#
using System;

class Test
{
    private readonly int x;

    private Test(int x)
    {
        this.x = x;
    }

    public static Test @return(int x)
    {
        return new Test(x);
    }

    public Test f()
    {
        return @return(x + 1);
    }

    public override string ToString()
    {
        return "[" + x + "]";
    }

    static void Main()
    {
        Console.WriteLine(@return(1).f().f().f().f());
    }
}
実行結果
[5]

C#でメソッドチェインが多用されるのはLinqやRxです。モナドの>>=も同じような目的で使うことができると考えても、当たらずと雖も遠からずではないでしょうか。

※ 実際には>>=は関数呼び出しの前後に処理を挟むことができるため、メソッドチェインよりも強力です。今回の範囲を超えるため詳細は省略しますが、興味があれば次の記事を参照してください。

モナド則を確認

結果の分かりやすさを考慮してリストで確認します。

※ 理解の便宜として一例を示しただけです。証明ではありません。

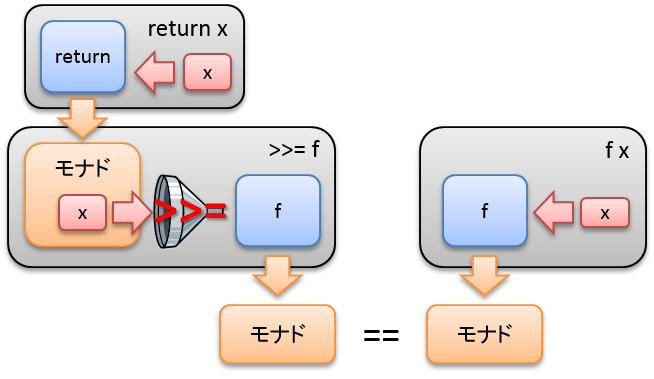
1. return x >>= f == f x

>>= の左側の return が消せることを要請します。

returnでモナドに値xを入れてからすぐ>>=でxを取り出して関数fに渡すのは、値xを関数fに直接渡すのと等しいです。左辺は出し入れしているだけです。

1.png

Prelude> let x = 1
Prelude> let f x = [x + 1]
Prelude> return x >>= f
[2]
Prelude> f x
[2]

当たり前に思えます。

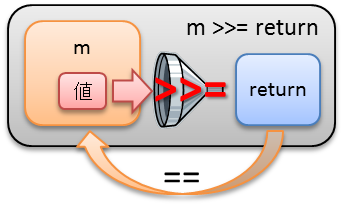
2. m >>= return == m

>>= の右側の return が消せることを要請します。

モナドmから>>=で値を取り出してreturnでまたモナドに入れれば、それは元のmと等しいです。左辺は出し入れしているだけです。

2.png

Prelude> let m = [1]
Prelude> m >>= return
[1]

これもまた当たり前に思えます。

return

C言語などの感覚でコードを見ると、ブロックの最後にreturnがあるとしっくり来ます。

例
inc x = return $ x + 1

test x = do
    y <- inc $ x * 2
    return y

main = do
    print =<< test 3

モナド則2により、関数testのreturnは省略できます。

test x = inc $ x * 2

コーディングスタイルの是非はともかく、このような変形を保証しているのがモナド則2です。

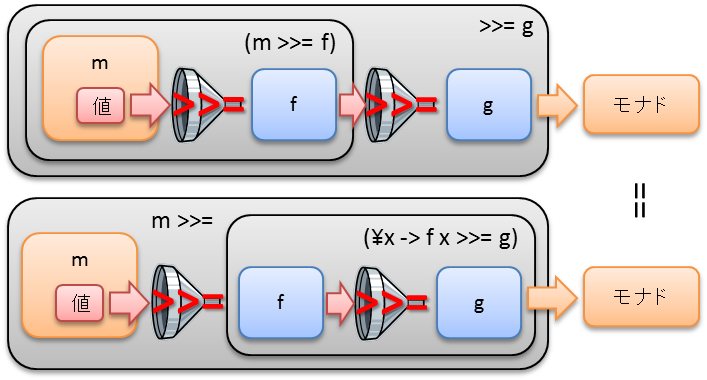
3. (m >>= f) >>= g == m >>= (\x -> f x >>= g)

あらかじめ関数が合成できることを要請します。

右辺のラムダ式を関数化して fg x = f x >>= g とおけば fg は f と g の関数合成に相当します。

※ f と g の間にモナドから値を取り出す操作 >>= が必要なため、単純な関数合成 g . f では型エラーとなります。(>>= g) . f とする必要があります。f >=> g とも書けます。（詳細は後述）

fg によって書き換えると (m >>= f) >>= g == m >>= fg となります。両辺とも m が f → g の順に渡されます。処理される順番が同じなので、f や g がどのような関数であっても結果は同じです。

3.png

Prelude> let m = [1]
Prelude> let f x = return $ x + 1
Prelude> let g x = return $ x * 2
Prelude> (m >>= f) >>= g
[4]
Prelude> m >>= (\x -> f x >>= g)
[4]

見かけはややこしいですが、理屈は当たり前です。

※ モナド則1と2を満たして3だけを満たさないものは、意図的に作ろうとしてもなかなか難しいです。詳細はコメントを参照してください。

注意

  1. >>= は左結合のため、左辺 (m >>= f) >>= g の括弧は外せます: m >>= f >>= g
    • m >>= (f >>= g) は型エラーになります。
  2. 右辺 m >>= (\x -> f x >>= g) のラムダ式の範囲を明示すると m >>= (\x -> (f x >>= g)) です。
    • m >>= ((\x -> f x) >>= g) ではありません。これは型エラーになります。\x -> f x をポイントフリー化すれば f となるため、前述の型エラーになる m >>= (f >>= g) と一致します。（やはりダメだということです）
  3. モナドに適用する関数同士は専用の演算子 >=> で合成できます: fg = f >=> g
    • >=> によって右辺 m >>= (\x -> f x >>= g) を書き換えれば m >>= (f >=> g) となります。これはあらかじめ関数を合成しているのが分かりやすい表記です。
    • m >>= (f >>= g) とは書けませんが、m >>= (f >=> g) とは書けるという見方もできます。

まとめ

モナドを実装する人が適切にreturnと>>=を実装すれば、モナド則に沿った「当たり前な動き」が実現されます。そうならないように実装することは可能ですが、それはモナドではありません。それを判定するのがモナド則だということのようです。

モナドを使うだけの人にとっては「コードを整理するためのヒント」になりそうですが、わざわざルールとして勉強しなくても、モナドの動きが分かっていれば同等の変形は自然と気付きそうです。

補足

補足情報です。よく分からなければ無視しても構いません。

モナド則3の書き換え

ここまで出て来たモナド則3の書き換えを並べます。

  1. (m >>= f) >>= g == m >>= (\x -> f x >>= g)（ラムダ式）
  2. (m >>= f) >>= g == m >>= fg where fg x = f x >>= g（関数化）
  3. (m >>= f) >>= g == m >>= ((>>= g) . f)（関数合成）
  4. (m >>= f) >>= g == m >>= (f >=> g)（専用の演算子）

演算子の使い分けにさえ慣れれば、4で考えるのがお勧めです。特に結合法則が読み取りやすいです。

>=> については次の記事が参考になります。

関数合成

モナド則3を普通の関数合成で書けば m >>= ((>>= g) . f) となります。パズルみたいな見た目です。意味が取りにくい書き方ですが、参考のため説明します。

考え方としては f x >>= g を f x と (>>= g) に分割して、引数 x を取り除き、f と (>>= g) を関数合成したのが (>>= g) . f です。

※ f と g の間にモナドから値を取り出す操作 >>= が入ることに注意します。(>>= g) は g がモナドを受け取るように変換された関数だと解釈します。（この変換を関数の持ち上げと表現します）

書き換える過程を示します。

  1. f x >>= g を f x とセクション (>>= g) に分割して、前者を後者の引数とします。
    • f x >>= g → (>>= g) (f x)
  2. (>>= g) と f を合成して、引数 x を括り出します。
    • (>>= g) (f x) → ((>>= g) . f) x
  3. ラムダ式の引数をそのまま適用している形になるため、引数を取り除きます。（ポイントフリースタイル）
    • \x -> ((>>= g) . f) x → (>>= g) . f

詳細は次の記事を参照してください。

モノイド対象

モナドは「自己関手の圏におけるモノイド対象」だと言われます。モナド則そのままでは分かりにくいですが、>=> で書き換えればモノイドの構造が現れます。

モナド則を再掲します。説明の都合上、モナド則3の関数名を変更しました。

  1. return x >>= f == f x
  2. m >>= return == m
  3. (m >>= g) >>= h == m >>= (\x -> g x >>= h)

モナドは何らかの関数から生成されたと考えて m = f x で書き換えます。

  1. return x >>= f == f x
  2. f x >>= return == f x
  3. (f x >>= g) >>= h == f x >>= (\x -> g x >>= h)

あちこちにモナド則3のラムダ式の g x >>= h と同じパターンが現れていることに注目します。それらを >=> で書き換えます: g x >>= h → (g >=> h) x

  1. (return >=> f) x == f x
  2. (f >=> return) x == f x
  3. (f >=> g) x >>= h == f x >>= (g >=> h)

(f >=> g) や (g >=> h) は合成された1つの関数と見なせるため、3の両辺は更に書き換えられます。

  • ((f >=> g) >=> h) x == (f >=> (g >=> h)) x

引数 x を取り除けば、モナド則は >=> によって関数を合成する規則に書き換わります。

  1. return >=> f == f
  2. f >=> return == f
  3. (f >=> g) >=> h == f >=> (g >=> h)

>=> を掛け算 * のようなものだと考えれば、return は 単位元 1 に相当します。

  1. 左単位元 1 * f == f
  2. 右単位元 f * 1 == f
  3. 結合法則 (f * g) * h == f * (g * h)

単位元を持ち結合法則を満たすものはモノイドです。

※ 逆元は要請されないため群ではありません。

詳細は次の記事を参照してください。

行列との比較

$\vec v$ をベクトル、$A,B$ を $\vec v$ に作用する行列とします。

行列とベクトルの積が =<< に対応します。

  • $A\vec v$ : A =<< v

行列同士の積が <=< に対応します。

  • $AB$ : A <=< B

結合法則より $AB\vec v=(AB)\vec v=A(B\vec v)$

  • $(AB)\vec v$ : (A <=< B) =<< v
  • $A(B\vec v)$ : A =<< (B =<< v)

演算子を逆向きにすればモナド則3そのものです。

  • $A(B\vec v) = (AB)\vec v$
  • A =<< (B =<< v) == (A <=< B) =<< v
  • (v >>= B) >>= A == v >>= (B >=> A)

行列を関数だと捉える見方については、以下の記事を参照してください。

参考

以下の記事を参考にしました。

モナド解説の金字塔です。（内容が重いためつまみ食いしかしていませんが・・・）

簡潔なモナドの説明です。「持ち上げ」の感覚が分かれば色々と見えて来ます。

モナド則3の右辺の式変形は、次の掲示板を参考にしました。

別の描き方でモナドを図示して説明した記事です。

それとはまた別の描き方による説明です。

ここで使用されている String diagram についての記事です。

関連記事

この記事で使用したモナド則の図は次の記事が初出です。以前は続編という位置付けでした。

図の要素は次の記事で導入しています。

F#に応用した記事があります。

この記事で使用したのと似たような箱で型を考える記事です。

240
201
6

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
240
201