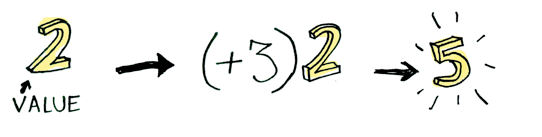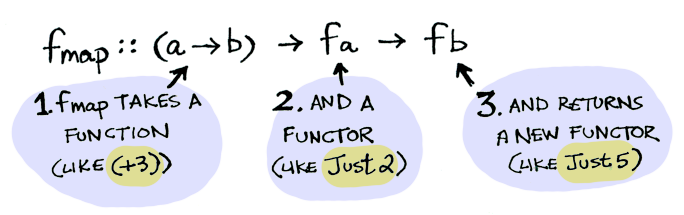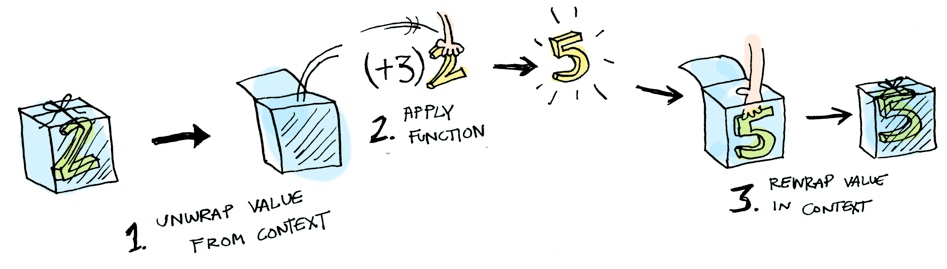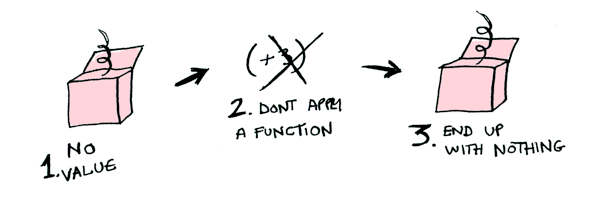モナドについて勉強していて見つけた英語記事を翻訳してみました。
誤訳等あれば編集リクエストやコメントください ![]()
原文: Functors, Applicatives, And Monads In Pictures - adit.io
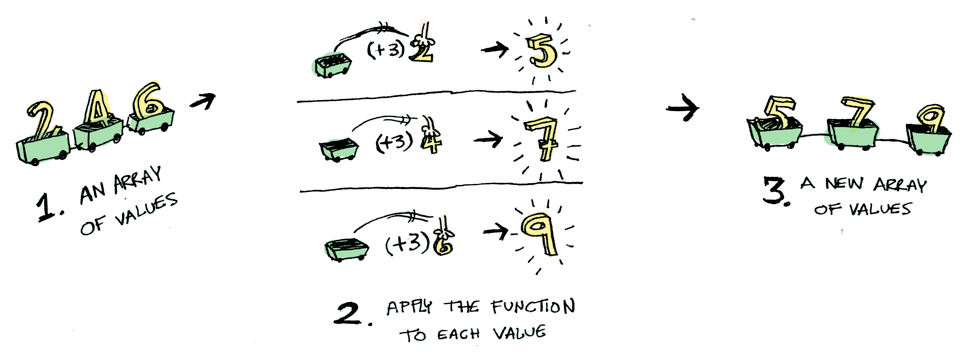
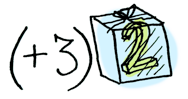
ここに単純な値(value)があります。
Prelude> 2
2
そして、私たちはこの値に関数を適用する方法を知っています。
Prelude> (+3) 2
5
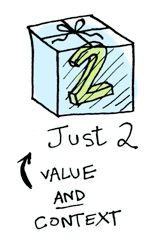
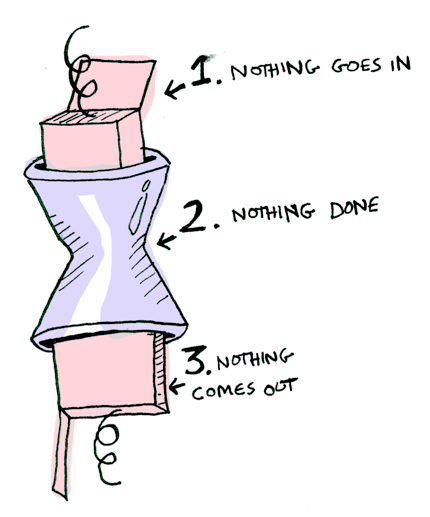
とても簡単ですね。それでは、ある状態(context)に値が入っていると仮定してみましょう。これからみなさんは値を入れられる状態のことを、箱だと考えてもらって構いません。
Prelude> Just 2
Just 2
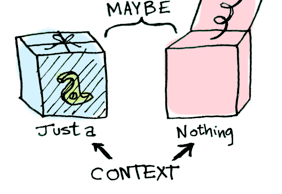
そして、この値に関数を適用したとき、 状態によって 異なる結果が返ります。この考え方に、Functor、Applicative、Monad、Arrowなどがもとづいています。Maybe データ型は2つの状態を定義できます。
data Maybe a = Nothing | Just a
Prelude> :type Just
Just :: a -> Maybe a
Prelude> :type Nothing
Nothing :: Maybe a
次に、Just a と Nothing それぞれに関数を適用したときどのような違いが出るか見てみましょう。先に Functor について話してみようと思います。
Functor
箱に入っている値に対して、普通の関数を適用することはできません。
Prelude> (+3) (Just 2)
ERR - No instance for (Num (Maybe a0))
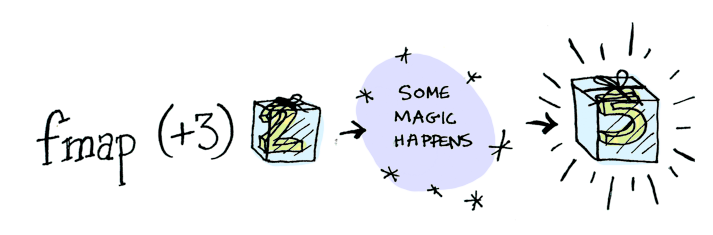
ここで fmap が登場します。fmapはその道の出身で、状態についてよく知っています。fmap は箱に入っている値にどのような関数を適用しなければならないか分かっています。例えば、 Just 2 に (+3) を適用してみましょう。 fmap を使ってみると…
> fmap (+3) (Just 2)
Just 5
ポン! fmap がやってくれました。では、どのように fmap は関数を適用する方法を知っていたのでしょうか?
Functorとは一体何だろうか?
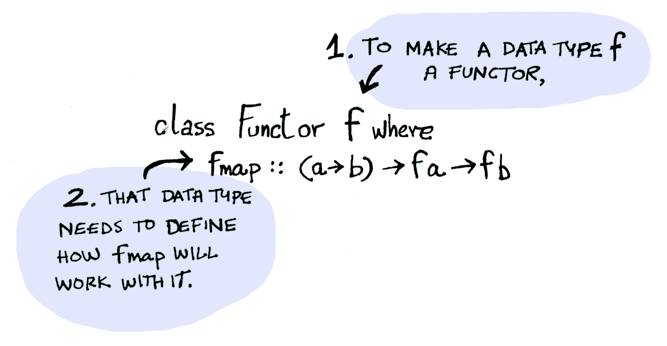
Functor は typeclass です。ここにその定義があります:
Functor は fmap を適用する方法を定義したデータ型です。ここにどのように fmap が動作するのかが出ています。
したがって、私たちは次のようにすることができます。
> fmap (+3) (Just 2)
Just 5
そして Maybe もまた Functor なので、fmap は魔法のように関数を適用してくれました。どのように fmap が Just と Nothing に適用されるかについてが次に出ています。
instance Functor Maybe where
fmap func (Just val) = Just (func val)
fmap func Nothing = Nothing
ここに fmap (+3) (Just 2) と打ったとき、裏でどんなことが起こるかが現れています。
それでは、 (+3) を Nothing に適用してみてください。
> fmap (+3) Nothing
Nothing
Maybe functorも知らないBill O'Reilly
マトリックスのモーフィアスのように、fmap は何をしなければならないか知っています。 Nothing で始まり、Nothing で終わる! fmap は禅です。では、Maybe データ型がなぜ存在するのか考えてみましょう。例えば、 Maybe がない言語で、データベースのレコードを扱おうとしたらこうなります。
post = Post.find_by_id(1)
if post
return post.title
else
return nil
end
しかし、Haskellは次のようにできます。
fmap (getPostTitle) (findPost 1)
もしも、findPost が投稿(post)を返すならば、getPostTitleでタイトルを得ることができます。 Nothing を返したら、Nothing を得るのです。とっても簡単じゃないですか? fmap の周囲表記(infix) バージョンは <$> で、次のように書くこともできます。
getPostTitle <$> (findPost 1)
ここにもう一つの例があります。リストに関数を適用したらどんなことが起こるでしょうか?
リストもやはり functor だったのです! ここにその定義があります。
instance Functor [] where
fmap = map
ではでは、最後にもう一つ例を。関数にまた別の関数を適用しようとしたらどんなことがおこるでしょうか?
fmap (+3) (+1)
Prelude> :type fmap (+3) (+1)
fmap (+3) (+1) :: (Functor ((->) b), Num b) => b -> b
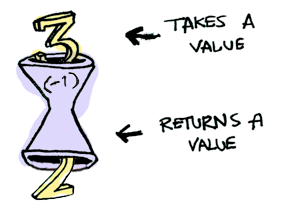
ここにある関数があります。
関数にまた別の関数を適用してみようと思います。
結果もやはり関数でした。
> import Control.Applicative
> let foo = fmap (+3) (+2)
> foo 10
15
したがって、関数も Functor なのです。
instance Functor ((->) r) where
fmap f g = f . g
関数に fmap を使用すると、関数の合成(function composition)をしたのと同じです。
Applicative
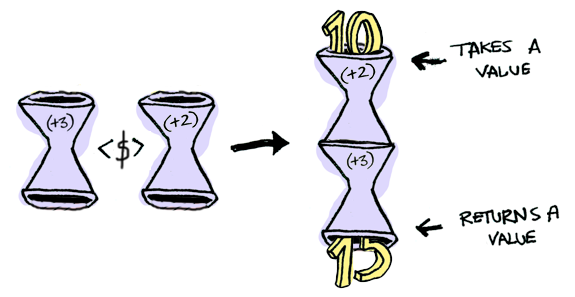
次の段階のApplicativeに進んでみましょう。Functorでやってみたように、箱に値を入れます。
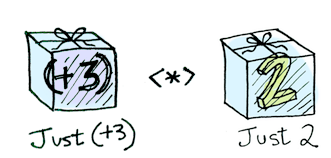
そして、関数もまた箱に入れられるのです!
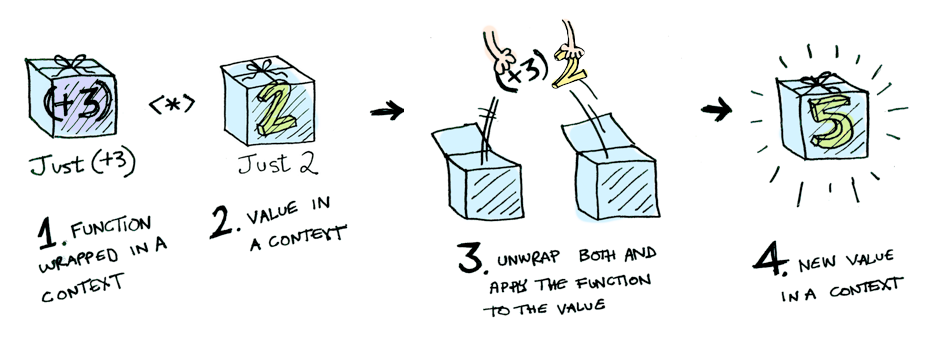
はい、じゃあ詳しく見てみましょう。Applicativeもバカじゃありません。Control.Applicative は <*> を定義していて、 箱の中の 値に、 箱の中の 関数を適用する方法を知っています。
なので、次のようなことができます。
Just (+3) <*> Just 2 == Just 5
<*> を使うと少し面白い結果を得ることができます。例えばこんな。
> [(*2), (+3)] <*> [1, 2, 3]
[2, 4, 6, 4, 5, 6]
ここでFunctorにはできなかったけど、Applicativeにはできることが出てきます。どうやって、中に値が入ってる2つの箱に、2つの引数を取る関数を適用するのでしょうか?
> (+) <$> (Just 5)
Just (+5)
> Just (+5) <$> (Just 4)
ERROR ??? WHAT DOES THIS EVEN MEAN WHY IS THE FUNCTION WRAPPED IN A JUST
Applicativeなら:
> (+) <$> (Just 5)
Just (+5)
> Just (+5) <*> (Just 3)
Just 8
Functor を横に追いやりながら Applicative は言います。
「大物は引数をいくつ取る関数だって扱えるんだぜ?」
「<$> と <*> を使ってオレは、箱を開いてみることができない関数どもに、箱の中の値を渡してやって、しまいに値を箱にいれて返すこともできるのさ! ぷははは!」
> (*) <$> Just 5 <*> Just 3
Just 15
functorが関数を適用するのを見ていたapplicative
でもちょっと待って! ここに同じことをする liftA2 もいます。
> liftA2 (*) (Just 5) (Just 3)
Just 15
Monad
モナドを学ぶ方法:
- 情報工学の博士号を取る
- ここでは博士号は要らないので取らない
モナドは新しい解法を提示しました。
Functorは箱に入っている値に関数を適用できます。
Applicativeは箱に入っている値に、箱に入っている関数を適用できます。
モナドは箱に入っている値に、 箱に入った値を返す 関数を適用できます。
モナドはこのようなことをする("bind"と呼ばれる) >>= という関数を持っています。
例を見てみましょう。これまでに見てきた Maybe はモナドです。
遊んでたJust aモナド
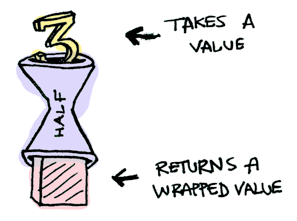
偶数に対してだけ動作する関数、halfがあると仮定してみましょう。
half x = if even x
then Just (x `div` 2)
else Nothing
値が入っている箱を入れてみるとどうなるでしょうか?
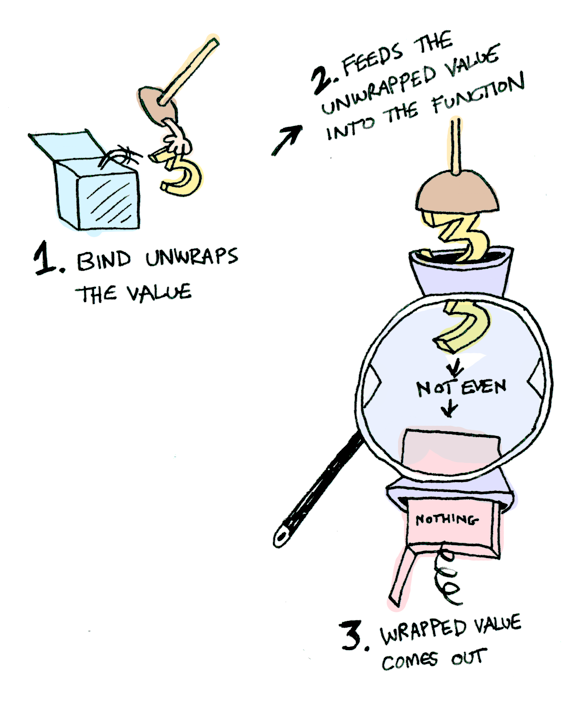
関数に値が入っている箱を押し込めたいなら、>>= が必要です。ここに >>= の写真があります。
どんなふうに動作するのか確認してみましょう。
> Just 3 >>= half
Nothing
> Just 4 >>= half
Just 2
> Nothing >>= half
Nothing
内部でどんなことが起こっているのでしょうか? Monadはまた別のtypeclassです。ここに定義の一部が載っています。
class Monad m where
(>>=) :: m a -> (a -> m b) -> m b
>>=は、
したがって、Maybeはモナドです。
instance Monad Maybe where
Nothing >>= func = Nothing
Just val >>= func = func val
ここに Just 3 についてどうやって動作しているか載っています!
Nothing を入れるともっと単純になります。
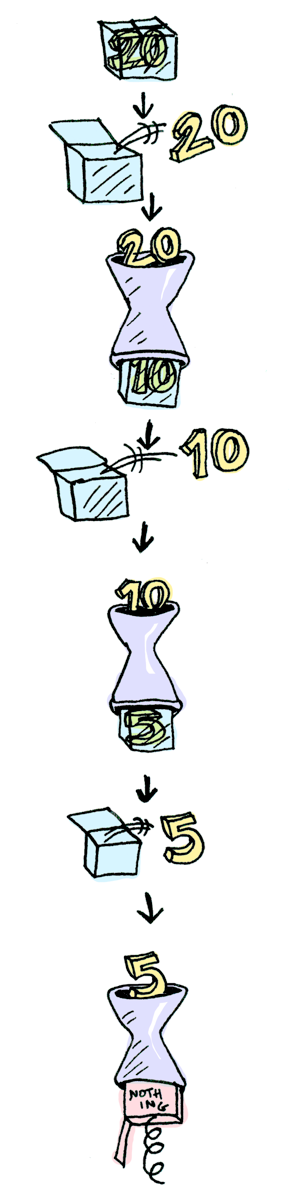
このようにチェーン(chain)で呼び出すこともできます。
> Just 20 >>= half >>= half >>= half
Nothing
カッチョイイです。もう私たちは Maybe が Functor であり、Applicative であり、Monad であることが分かりました。
それではそろそろ、IOモナドの例に行ってみましょう。
訳注: 数字の10ではなく、英語のIO
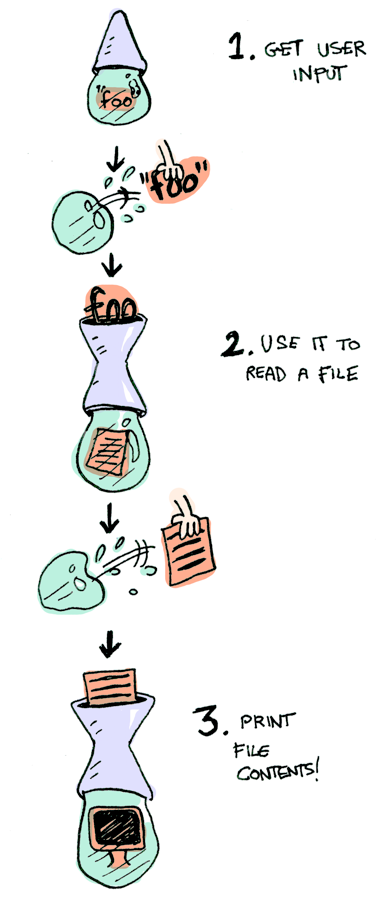
3つの特別な関数があります。 getLine は引数を取らず、ユーザの入力を受け取ります。
getLine :: IO String
readFile は文字列(ファイル名)を受け取り、ファイルの中身を返します。
readFile :: FilePath -> IO String
putStrLn は文字列を受け取り出力します。
putStrLn :: String -> IO ()
ここに出てきた3つの関数は普通の値を受け取り(または何も受け取らず)、値が入っている箱を返します。したがって、私たちはこれを >>= でつなぐことができます。
getLine >>= readFile >>= putStrLn
なんということでしょう! モナドのショーが巻き起こりました!
付け加えると、Haskellはこのモナドについて、do というシュガーシンタクスを提供してくれています。
foo = do
filename <- getLine
contents <- readFile filename
putStrLn contents
まとめ
- functorは
Functor型クラスを実装したデータ型。 - applicativeは
Applicative型クラスを実装したデータ型。 - モナドは
Monad型クラスを実装したデータ型。 -
Maybeはこの3つをすべて実装しており、functorでありapplicativeでありモナドでもある。
この3つの違いは何か?
- functor:
fmapや<$>を使って、箱の中の値に関数を適用できる - applicative:
liftAや<*>を使って、箱のなかの関数を箱の中の値に適用できる - モナド:
liftMや>>=を使って、箱に入った値を返す関数を箱の中の値に適用できる
わたしたちはみんな、モナドというものが簡単で粋な概念だということについて、同意することと思います。このガイドで満足するのはまだ早いです。LYAH’s section on Monadsをチェックしてみてください。Miranがすでにモナドに関する深く素晴らしい働きをしているので、だいぶざっくり説明してきました。
ロシア語バージョンもあります。もっとモナドと絵を見たい方は three useful monadsを見てみてください。