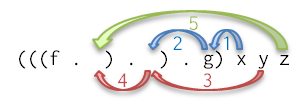
引数が複数ある時の関数合成は直感的な理解が困難です。あまり理解は追及しないで、機械的な式変形や解釈を試みました。
※ ちょっとした思い付きのようなもののため、どのような場面で有用なのかは未検証です。
この記事はHaskell 超入門シリーズの番外編です。
【追記 2016.7.1】似たような記事を見付けました。相互に独立ですが、観察すれば似たようなことに気付くのだと思いました。
- @necojackarc ポイントフリースタイルへの道 〜最大公約数編〜 2015.7.3
【追記 2016.7.1】同じテーマを扱った記事です。
- @etoilevi Haskellの関数合成、または (.) 関数 2015.6.13
関数合成を進める
1引数の関数合成は簡単ですが、多引数に拡張できる形での式変形を導入します。
f :: a -> a
g :: a -> a
$→.の書き換えでは、引数を括弧の外に出します。括弧がなければ式を囲みます。
-
f $ g x→(f $ g x)→(f . g) x
$が足りない時は、中置演算子をセクションで分断して$を挟みます。
-
1 + 1→(1 +) $ 1 -
(f . g) x→((f .) $ g) x
2引数
gの引数を増やします。
f :: a -> a
g :: a -> a -> a
$→.の書き換えでは、最後の引数を括弧の外に出します。$が足りなければ水増しします。
f $ g x y- 式を括弧で囲む:
(f $ g x y) -
$→.:(f . g x) y -
$を水増し:((f .) $ g x) y -
$→.:((f .) . g) x y
3引数
gの引数を増やします。
f :: a -> a
g :: a -> a -> a -> a
f $ g x y z- 式を括弧で囲む:
(f $ g x y z) -
$→.:(f . g x y) z -
$を水増し:((f .) $ g x y) z -
$→.:((f .) . g x) y z -
$を水増し:(((f .) .) $ g x) y z -
$→.:(((f .) .) . g) x y z
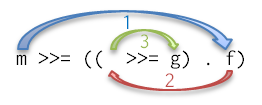
モナド則3の右辺
少し違うパターンです。ラムダ式の部分を関数合成で書き換えます。
m >>= (\x -> f x >>= g)-
$を水増し:m >>= (\x -> (>>= g) $ f x) - 式を括弧で囲む:
m >>= (\x -> ((>>= g) $ f x)) -
$→.:m >>= (\x -> ((>>= g) . f) x) - ポイントフリースタイル:
m >>= ((>>= g) . f)
モナド則については、次の記事が参考になるかもしれません。
- @7shi: Haskell - モナド則がちょっと分かった? - Qiita 2014.12.1
関数合成を外す
逆方向の式変形です。1引数の場合から見ます。
f :: a -> a
g :: a -> a
.→$の書き換えでは、引数を括弧の中に入れます。引数を適用するたびに合成が解除されると解釈できます。
-
(f . g) x→(f $ g x)
セクションの後の$は外して、引数をセクションに適用します。
-
(1 +) $ 1→(1 + 1) -
((f .) $ g) x→((f . g)) x
無駄な括弧があれば整理します。
-
(f $ g x)→f $ g x -
(1 + 1)→1 + 1 -
((f . g)) x→(f . g) x
2引数
gの引数を増やします。
f :: a -> a
g :: a -> a -> a
.→$の書き換えは右から行います。最初の引数を括弧の中に入れます。
((f .) . g) x y-
.→$(右から):((f .) $ g x) y - セクションに適用:
((f . g x)) y -
.→$:((f $ g x y)) - 括弧を整理:
f $ g x y
3引数
gの引数を増やします。
f :: a -> a
g :: a -> a -> a -> a
(((f .) .) . g) x y z-
.→$(右から):(((f .) .) $ g x) y z - セクションに適用:
(((f .) . g x)) y z -
.→$(右から):(((f .) $ g x y)) z - セクションに適用:
(((f . g x y))) z -
.→$:(((f $ g x y z))) - 括弧を整理:
f $ g x y z
引数不足
.→$の書き換え時に引数が足りないときは、式をラムダ式で包んで引数を補います。既にラムダ式で包まれていれば、引数は後ろに追加します。
((f .) .) . g- ラムダ式化して引数を補う:
\x -> (((f .) .) . g) x -
.→$(右から):\x -> (((f .) .) $ g x) - セクションに適用:
\x -> (((f .) . g x)) - 引数を追加:
\x y -> (((f .) . g x)) y -
.→$(右から):\x y -> (((f .) $ g x y)) - セクションに適用:
\x y -> (((f . g x y))) - 引数を追加:
\x y z -> (((f . g x y))) z -
.→$:\x y z -> (((f $ g x y z))) - 括弧を整理:
\x y z -> f $ g x y z
.の数だけ引数が出て来ました。
モナド則3の右辺
上で書き換えたものを元に戻します。
m >>= ((>>= g) . f)- ラムダ式化して引数を補う:
m >>= (\x -> ((>>= g) . f) x) -
.→$:m >>= (\x -> ((>>= g) $ f x)) - セクションに適用:
m >>= (\x -> ((f x >>= g))) - 括弧を整理:
m >>= (\x -> f x >>= g)
関数合成の解釈
関数合成がネストしているとどう解釈して良いのか戸惑います。意味の把握は難しいですが、先ほど示した式変形に沿えば、計算の流れを追うことはできます。
引数を適用するたびに合成が解除されて、計算が内部に移動します。式変形をしないで、適用の流れだけを追うイメージです。
- 引数を適用:
(((f .) .) $ g x) y z - セクションに適用:
(((f .) . g x)) y z - 引数を適用:
(((f .) $ g x y)) z - セクションに適用:
(((f . g x y))) z - 引数を適用:
(((f $ g x y z)))
モナド則3の右辺(関数合成版)
式変形せずに計算の流れを追います。
-
mから値を取り出してfに適用:((>>= g) . (m >>= f)) -
fの戻り値をセクションに適用:(((m >>= f) >>= g)) -
gに適用:(m >>= f) >>= g
計算過程を式変形で表現した結果、モナド則3の左辺に一致しました。