前回はコベクトルによりスカラーを返す関数を複数まとめられることを見ました。今回はベクトルを返す関数を行列で表します。双対ベクトル空間のイメージを伝えることを目的としています。比較用のプログラミング言語にはPythonを使用して、計算にはNumPyの結果を添えます。
シリーズの記事です。
- 見積りで考える内積
- 関数で考えるコベクトル
- 関数で考える行列 ← この記事
- 関数で考える双対性
- コベクトルで考えるパーセプトロン
コベクトルによる関数
前回紹介した3つの引数から指定した値を返すコベクトルを再掲します。
※ 以後、importは省略します。
>>> from numpy import *
>>> GetX = [1, 0, 0]
>>> GetY = [0, 1, 0]
>>> GetZ = [0, 0, 1]
>>> dot(GetX, [1, 2, 3])
1
>>> dot(GetY, [1, 2, 3])
2
>>> dot(GetZ, [1, 2, 3])
3
\begin{align}
\mathrm{GetX}
&\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
=\begin{pmatrix}1 & 0 & 0\end{pmatrix}
\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
=1 \\
\mathrm{GetY}
&\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
=\begin{pmatrix}0 & 1 & 0\end{pmatrix}
\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
=2 \\
\mathrm{GetZ}
&\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
=\begin{pmatrix}0 & 0 & 1\end{pmatrix}
\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
=3
\end{align}
多対一
前回、複数の関数に同じ引数を渡せることを見ました。先ほどの関数で試します。
>>> dot([GetX,GetY,GetZ],[1,2,3])
array([1, 2, 3])
\begin{align}
\begin{pmatrix}\mathrm{GetX} \\ \mathrm{GetY} \\ \mathrm{GetZ}\end{pmatrix}
\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
&=\left(\begin{array}{r}
\mathrm{GetX} \begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix} \\
\mathrm{GetY} \begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix} \\
\mathrm{GetZ} \begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
\end{array}\right) \\
&=\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
\end{align}
戻り値全体を1つのベクトルと見なせば、引数をそのまま返していることに気付きます。コベクトルにより構成される行列が単位行列になることに注目すれば自然な結果です。
\begin{pmatrix}\mathrm{GetX} \\ \mathrm{GetY} \\ \mathrm{GetZ}\end{pmatrix}
=\begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}
行列による関数
先ほどの例を1つの関数による1つの結果と考えれば、コベクトルにより構成される行列が1つの関数だと見なせます。
>>> Id=[GetX,GetY,GetZ]
>>> dot(Id,[1,2,3])
array([1, 2, 3])
\begin{aligned}
&\mathrm{Id}=\begin{pmatrix}\mathrm{GetX} \\ \mathrm{GetY} \\ \mathrm{GetZ}\end{pmatrix} \\
&\mathrm{Id}
\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
=\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
\end{aligned}
並べ方をずらせば巡回させる関数も作れます。
>>> Rotate=[GetY,GetZ,GetX]
>>> dot(Rotate,[1,2,3])
array([2, 3, 1])
\begin{aligned}
&\mathrm{Rotate}=\begin{pmatrix}\mathrm{GetY} \\ \mathrm{GetZ} \\ \mathrm{GetX}\end{pmatrix} \\
&\mathrm{Rotate}
\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
=\begin{pmatrix}2 \\ 3 \\ 1\end{pmatrix}
\end{aligned}
このように行列を関数と見なして、必要に応じてコベクトルに分割して解釈することができます。
結合性
2回連続でずらすことも可能です。
>>> dot(Rotate,dot(Rotate,[1,2,3]))
array([3, 1, 2])
\mathrm{Rotate}\left(\mathrm{Rotate}
\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}\right)
=\begin{pmatrix}3 \\ 1 \\ 2\end{pmatrix}
掛け算で $a(bc)=(ab)c$ のように先に計算する組み合わせを変えても結果が同じなのと同様に、先に Rotate 同士の積を計算することが可能です。
>>> dot(dot(Rotate,Rotate),[1,2,3])
array([3, 1, 2])
\left\{(\mathrm{Rotate})(\mathrm{Rotate})\right\}
\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
=\begin{pmatrix}3 \\ 1 \\ 2\end{pmatrix}
このように計算順序を変更しても結果が変わらないことを結合性と呼びます。行列の積の演算方法は結合性が確保されるように考えて作られています。
関数合成
行列による関数の積を関数合成と見なして新しい関数に割り当てることが可能です。
>>> Rotate2=dot(Rotate,Rotate)
>>> dot(Rotate2,[1,2,3])
array([3, 1, 2])
\begin{aligned}
&\mathrm{Rotate2}=(\mathrm{Rotate})(\mathrm{Rotate}) \\
&\mathrm{Rotate2}
\begin{pmatrix}1 \\ 2 \\ 3\end{pmatrix}
=\begin{pmatrix}3 \\ 1 \\ 2\end{pmatrix}
\end{aligned}
3回Rotateすれば元に戻りますが、関数合成の結果が単位行列になることが確認できます。
>>> Rotate3=dot(Rotate2,Rotate)
>>> dot(Rotate3,[1,2,3])
array([1, 2, 3])
>>> Rotate3
array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
(\mathrm{Rotate2})(\mathrm{Rotate})
=\begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}
入力数・出力数
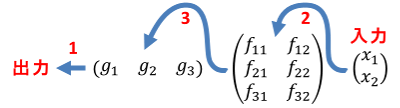
行列を関数と見なせば、行列のサイズが引数の要素数(入力数)と戻り値の要素数(出力数)を表していると解釈できます。
(X, X) -> F -> (X, X, X)
(X, X, X) -> G -> X
\begin{aligned}
F&:\quad\scriptsize{出力数3}\normalsize{\Biggr\{
\overbrace{\begin{pmatrix}f_{11} & f_{12} \\ f_{21} & f_{22} \\ f_{31} & f_{32}\end{pmatrix}}^{入力数2}} \\
G&:\quad\scriptsize{出力数1}\normalsize{\{
\overbrace{\begin{pmatrix}g_1 & g_2 & g_3\end{pmatrix}}^{入力数3}}
\end{aligned}
$F$ と $G$ を連続で計算する場合、先に計算する $F$ の出力数が、後続の $G$ の入力数と一致している必要があります。
F→
\underbrace{\begin{pmatrix}t_1 \\ t_2 \\ t_3\end{pmatrix}}_{中間の値}
→G
$F$ と $G$ を合成して $GF$ とした状況を、成分表示で確認します。
\underbrace{GF}_{合成}
=\overbrace{\begin{pmatrix}g_1 & g_2 & g_3\end{pmatrix}}^{入力数3}
\quad\scriptsize{出力数3}\normalsize{\Biggr\{
\begin{pmatrix}f_{11} & f_{12} \\ f_{21} & f_{22} \\ f_{31} & f_{32}\end{pmatrix}}
関数合成 $GF$ は計算順 $F$ → $G$ とは表記順が逆です。
$G$ の入力数と $F$ の出力数が一致しなければ合成できません。
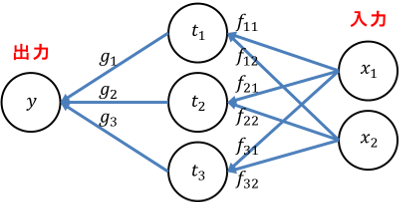
計算の流れ
入力と出力を含めた計算の流れを示します。赤い数字は要素数を表します。
値に着目して模式化します。
\underbrace{y}_{出力}
\xleftarrow{G}
\underbrace{\begin{pmatrix}t_1 \\ t_2 \\ t_3\end{pmatrix}}_{中間の値}
\xleftarrow{F}
\underbrace{\begin{pmatrix}x_1 \\ x_2\end{pmatrix}}_{入力}
パーセプトロン風に図を描きます。行列表記に合わせて計算の流れを右から左とします。
1 つのノードに対する複数の入力は和を取ります。
$x$ から $t$ を結ぶ線に注目します。このうち $f_{21}$ を例に取れば、添え字を $2←1$ と解釈することで、線が結ぶノード $t_2←x_1$ の添え字に対応することが分かります。模式化すると以下の通りです。
t_2 \xleftarrow{f_{21}} x_1
他の線も同じパターンになることを確認してください。
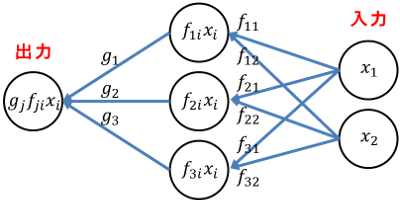
テンソルのフロー
ノードの添え字を変数にして $x_i$ や $t_j$ と表記すれば、それらを結ぶ線は $f_{ji}$ となります。
t_j \xleftarrow{f_{ji}} x_i
最後のステップまで含めれば以下のようなフローとなります。
y \xleftarrow{g_j} t_j \xleftarrow{f_{ji}} x_i
この関係を次のような式で表すのがテンソル代数です。
\begin{aligned}
t_j&=f_{ji}x_i \\
y&=g_jt_j \\
&=g_jf_{ji}x_i
\end{aligned}
同じ添え字が複数ある場合に和を取るというアインシュタインの縮約記法によって、総和記号 $\sum$ が省略されています。これにより個々の関係が全体に拡大されます。
テンソル代数の表現方法は、行列に添え字の関係を追加したものです。
\begin{aligned}
\boldsymbol{t}&=\boldsymbol{Fx} \\
y&=\boldsymbol{Gt} \\
&=\boldsymbol{GFx}
\end{aligned}
ノードの値をテンソル代数で表記すれば、テンソルの流れ(フロー)が見えて来ます。
\underbrace{g_jf_{ji}x_i}_{出力}
\xleftarrow{g_j}
\underbrace{f_{ji}x_i}_{中間の値}
\xleftarrow{f_{ji}}
\underbrace{x_i}_{入力}
1 つのノードに対する複数の入力の和を取ることが、テンソル代数ではアインシュタインの縮約記法によって表現されます。