Go to Qiita Advent Calendar Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@00b012deb7c8

Python で巡回経路探索（TSP）を現実化：OSRM を用いた道路距離の適用

Posted at

はじめに

これまでに扱った要素は大きく2つあります。
1つは、複数地点を効率よく回る 巡回経路探索（Traveling Salesman Problem, TSP） を Python で実装し、ユークリッド距離（直線距離）を使ってルート最適化を行ったこと。
もう1つは、OSRM（Open Source Routing Machine） を Docker で構築し、実際の道路に基づいた移動距離・所要時間を取得できるようにしたことです。

巡回経路探索・TSP
OSRMセットアップ

今回はこれらを組み合わせ、
TSPの距離計算を「直線距離」から「OSRMが返す道路距離」に置き換えることで、
より現実的な巡回ルート探索や片道ルート探索を実装していきます。

準備

本記事では、あらかじめ OSRM サーバがローカルで稼働 していることを前提とします。
（Docker でのセットアップ手順は割愛。http://localhost:5000 にアクセスできる状態にしておいてください）

前提の確認

  • OSRM サーバ稼働確認
    ブラウザで次の形式の URL にアクセスし、JSON が返ることを確認します。
    http://localhost:5000/route/v1/driving/{lon1},{lat1};{lon2},{lat2}?overview=false
  • Python 実行環境
    Windows 11 + Python 3.x（VS Code + Git Bash 想定）
  • 必要ライブラリ
    • HTTP クライアント（例：requests を想定）

本章のゴール

  • Python から OSRM API を呼び、2 点間の道路距離（m）と所要時間（秒） を取得できること。
  • 本記事以降で使う 距離行列 作成の前段として、「2 点間距離の取得関数」 を用意すること。

関数の役割

  • 引数： (lon, lat) 形式の座標を 2 点渡す
  • 戻り値： (distance_meters, duration_seconds) を返す
  • 内部処理： OSRM API にアクセスし、結果の JSON から必要な値を取り出す
import requests

def get_osrm_distance(from_coord, to_coord):
    """
    from_coord, to_coord: (lon, lat) のタプル
    戻り値: (距離[m], 所要時間[秒])
    """
    url = f"http://localhost:5000/route/v1/driving/{from_coord[0]},{from_coord[1]};{to_coord[0]},{to_coord[1]}"
    res = requests.get(url, params={"overview": "false"})
    data = res.json()
    return data["routes"][0]["distance"], data["routes"][0]["duration"]

# 動作確認例
if __name__ == "__main__":
    tokyo = (139.7671, 35.6812)   # 東京駅
    shibuya = (139.7013, 35.6580) # 渋谷駅
    dist, dur = get_osrm_distance(tokyo, shibuya)
    print(f"距離: {dist/1000:.2f} km, 所要時間: {dur/60:.1f} 分")

距離行列の作成

TSP（巡回経路探索、あるいは片道ルート探索）を解くためには、
「各地点間の距離」を一覧化した 距離行列（distance matrix） が必要です。

ここでは、前章で用意した get_osrm_distance(from_coord, to_coord) を利用して、
地点リストから距離行列を作成する関数を用意します。

関数の役割

  • 引数：複数の座標リスト（[(lon, lat), (lon, lat), ...]）
  • 戻り値：2次元リスト（dist_matrix[i][j] が i→j の距離[m]）
  • 内部処理：各地点の組み合わせについて OSRM API を呼び出し、距離を埋める
import itertools

def build_distance_matrix(coords):
    """
    OSRM を用いて距離行列を作成する
    coords: [(lon, lat), (lon, lat), ...]
    戻り値: dist_matrix[i][j] が i→j の距離[m]
    """
    n = len(coords)
    dist_matrix = [[0.0] * n for _ in range(n)]

    for i, j in itertools.permutations(range(n), 2):
        dist, _ = get_osrm_distance(from_coord=coords[i], to_coord=coords[j])
        dist_matrix[i][j] = dist

    return dist_matrix
  • OSRM API を地点の組み合わせごとに呼び出すため、地点数が多いと処理時間が長くなります
  • 5〜10地点程度であれば問題ありませんが、大規模データではバルクAPI（/table エンドポイント）利用を検討すると効率的です

TSPアルゴリズムの適用

距離行列が準備できたので、これを使って 巡回経路探索（TSP） を解きます。
ここでは、過去記事で扱ったシンプルな手法を再利用します。

使用するアルゴリズム

  • 最近近傍法（Nearest Neighbor, NN）
    ある地点から最も近い未訪問地点を順に選ぶ簡易手法。計算が速い。
  • 2-opt 改善法
    初期ルートに対し、辺の入れ替えで距離が短くなる場合に更新していく改良手法。

関数の役割

  • 入力：距離行列（dist_matrix[i][j] が i→j の距離[m]）
  • 出力：訪問順序（地点インデックスのリスト）と総距離
  • 流れ：
    1. 最近近傍法で初期ルートを生成
    2. 2-opt 改善法でルートを最適化
def total_distance(route, dist_matrix):
    """
    巡回ルート(route)の総距離を計算（最後は出発点に戻る）
    route: [0, 2, 1, ...] のような訪問順（出発点＝先頭要素）
    """
    n = len(route)
    d = 0.0
    for i in range(n):
        a = route[i]
        b = route[(i + 1) % n]  # 最後は出発点に戻る
        d += dist_matrix[a][b]
    return d


def nearest_neighbor(dist_matrix, start=0):
    """
    最近近傍法で初期ルートを作成（巡回ルート）
    戻り値: (route, total_dist)
    """
    n = len(dist_matrix)
    unvisited = set(range(n))
    route = [start]
    unvisited.remove(start)
    current = start
    while unvisited:
        nxt = min(unvisited, key=lambda j: dist_matrix[current][j])
        route.append(nxt)
        unvisited.remove(nxt)
        current = nxt
    return route, total_distance(route, dist_matrix)


def two_opt(route, dist_matrix, max_iterations=1000):
    """
    2-opt 改善法でルートを改良（巡回ルート前提）
    戻り値: (best_route, best_distance)
    """
    best = route[:]
    best_dist = total_distance(best, dist_matrix)
    n = len(best)

    improved = True
    it = 0
    while improved and it < max_iterations:
        improved = False
        it += 1
        for i in range(1, n - 1):
            for k in range(i + 1, n):
                a, b = best[i - 1], best[i]
                c, d = best[k % n], best[(k + 1) % n]
                delta = (dist_matrix[a][c] + dist_matrix[b][d]) - (dist_matrix[a][b] + dist_matrix[c][d])
                if delta < -1e-9:
                    best[i:k + 1] = reversed(best[i:k + 1])
                    best_dist += delta
                    improved = True
    return best, best_dist

前回の記事では、巡回ルートだけでなく 片道ルート（始点と終点が異なる場合） にも対応できるように拡張しました。
本記事のアルゴリズム部分はそのまま利用でき、「距離の計算をユークリッド距離から OSRM に置き換える」 だけで巡回ルート・片道ルートのどちらにも適用可能です。

実行例

最後に、実際の地点を入力して TSP を解いてみます。
ここでは例として、次の 8 地点を使用します。

  • 東京駅
  • 押上（スカイツリー）
  • 浅草（雷門）
  • お台場（ダイバーシティ）
  • 羽田空港 第3ターミナル
  • 六本木ヒルズ
  • 吉祥寺駅
  • 品川駅

実行の流れ

  1. 各地点の座標を (lon, lat) で定義
  2. build_distance_matrix で距離行列を作成（OSRMを利用）
  3. nearest_neighbor で初期ルートを作成
  4. two_opt でルートを改善
  5. 結果（訪問順序と総距離）を表示
# 実行例: 8 地点で TSP を実行（OSRM 距離ベース）
# 前提: get_osrm_distance, build_distance_matrix, nearest_neighbor, two_opt が定義済み

# 1) 地点の定義（(lon, lat)）
names = [
    "東京駅",
    "押上（スカイツリー）",
    "浅草（雷門）",
    "お台場（ダイバーシティ）",
    "羽田空港 第3ターミナル",
    "六本木ヒルズ",
    "吉祥寺駅",
    "品川駅",
]

coords = [
    (139.7671, 35.6812),  # 東京駅
    (139.8107, 35.7101),  # 押上（スカイツリー）
    (139.7967, 35.7110),  # 浅草（雷門）
    (139.7750, 35.6250),  # お台場（ダイバーシティ）付近
    (139.7840, 35.5494),  # 羽田空港 第3T 付近
    (139.7304, 35.6605),  # 六本木ヒルズ
    (139.5826, 35.7033),  # 吉祥寺駅
    (139.7386, 35.6285),  # 品川駅
]

# 2) 距離行列の作成（OSRM）
dist_matrix = build_distance_matrix(coords)

# 3) 最近近傍法で初期ルート（東京駅を始点にする場合は start=0）
init_route, init_len = nearest_neighbor(dist_matrix, start=0)

# 4) 2-opt で改善
best_route, best_len = two_opt(init_route, dist_matrix)

# 5) 結果表示
def route_to_names(route, cycle=True):
    s = " → ".join(names[i] for i in route)
    return s + (f" → {names[route[0]]}" if cycle else "")

print("NN 初期ルート:", init_route, f"距離: {init_len/1000:.2f} km")
print("    表示     :", route_to_names(init_route))

print("2-opt 改善後 :", best_route, f"距離: {best_len/1000:.2f} km")
print("    表示     :", route_to_names(best_route))

# ------------------------------
# NN 初期ルート: [0, 2, 1, 5, 7, 3, 4, 6] 距離: 95.32 km
#    表示     : 東京駅 → 浅草（雷門） → 押上（スカイツリー） → 六本木ヒルズ → 品川駅 → お台場（ダイバーシティ） → 羽田空港 第3ターミナル → 吉祥寺駅 → 東京駅
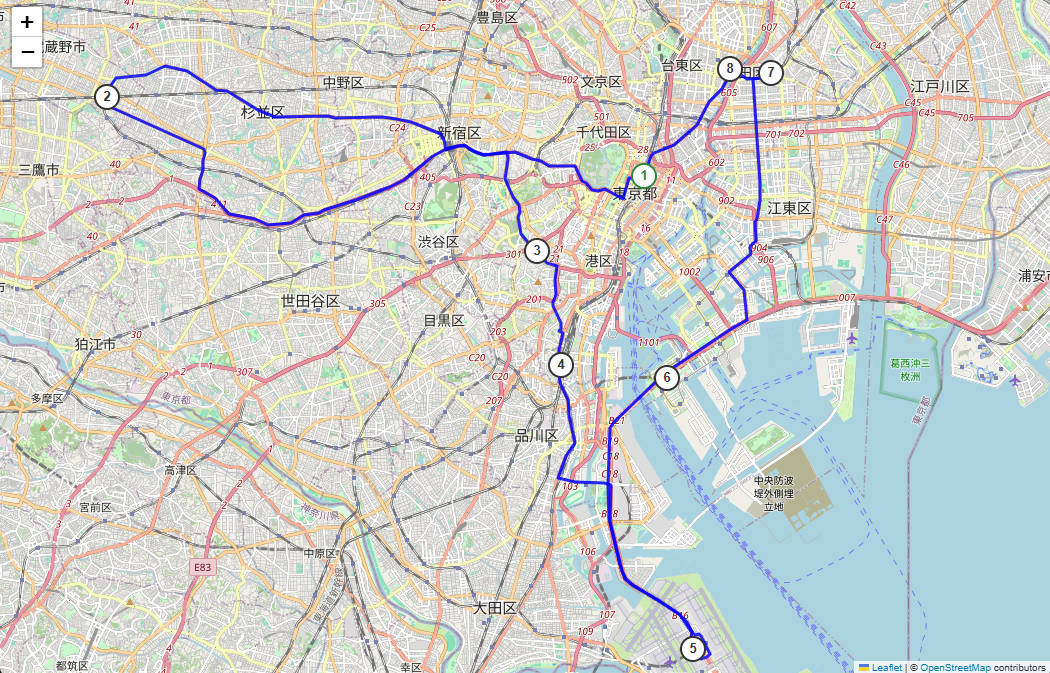
# 2-opt 改善後 : [0, 6, 5, 7, 4, 3, 1, 2] 距離: 86.42 km
#    表示     : 東京駅 → 吉祥寺駅 → 六本木ヒルズ → 品川駅 → 羽田空港 第3ターミナル → お台場（ダイバーシティ） → 押上（スカイツリー） → 浅草（雷門） → 東京駅
# ------------------------------

2-opt の結果

2d4580c139650ddec632-1.png

まとめ

本記事では、これまでユークリッド距離（直線距離）で実装していた巡回経路探索（TSP）を、
OSRM が返す道路距離に置き換えることで、より現実的なルート探索を実現しました。

ポイント整理

  • OSRM サーバをローカルで稼働させ、Python から距離・所要時間を取得
  • 得られた値を用いて 距離行列 を構築
  • 既存の TSP アルゴリズム（最近近傍法＋2-opt 改善法）に組み込み
  • 直線距離と比較して、実際の道路に基づく現実的なルートが得られることを確認
  • 片道ルート拡張にもそのまま適用可能

今後の展望

  • OSRM /table エンドポイントを使った効率的な距離行列の作成
  • VRP（Vehicle Routing Problem、複数車両の配車計画）への拡張
  • 時間帯や交通規制を考慮したルート探索

これにより、「TSPを道路距離で解く」ための基本的な仕組みが整いました。
次のステップとしては、地点数を増やして処理性能を検証したり、
より高度なアルゴリズム（遺伝的アルゴリズムや局所探索法）との組み合わせも検討できます。

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?