複数地点を効率よく回る経路を求める ― Pythonで巡回／片道ルート探索を実装

1. はじめに

前回の記事では、複数地点を効率よく回る経路を求める 巡回経路探索（TSP） を取り上げ、
基本的な手法として「最近近傍法（Nearest Neighbor, NN）」と「2-opt 改善法」を実装しました。

今回はその続編として、始点と終点を任意に設定できるようにし、
「巡回ルート（出発点に戻る）」だけでなく「片道ルート（出発点と到着点が異なる）」にも対応できるように拡張していきます。

複数地点を効率よく回る経路を求める ― Pythonで巡回経路探索（TSP）入門

2. 巡回ルートと片道ルート

巡回ルート

出発点と到着点が同じになるルートです。
例えば、観光で
「A駅から出発して複数の観光スポットを回り、再びA駅に戻る日帰りコース」のようなイメージです。

片道ルート

出発点と到着点が異なるルートです。
例えば、
「A駅から出発して観光スポットを巡り、最後はB駅で終了する観光コース」のようなイメージです。

巡回と片道はどちらが優れているというものではなく、
利用シーンに応じてどちらを採用するかが決まるのが特徴です。

3. 実装拡張のポイント

前回の実装では「出発点に戻る巡回ルート」を前提にしていました。
今回はこれを拡張して、以下のような設定に対応できるようにします。

• 始点を任意に指定できる
• 終点を任意に指定できる
• 巡回ルート / 片道ルート を切り替え可能にする

4. 最近近傍法（NN）の拡張

前回の実装では「始点＝終点」で固定した巡回ルートしか扱えませんでした。
ここでは、始点と終点を任意に指定できるように拡張します。

実装の考え方

• 引数で start と end を受け取る
• end が指定されていない場合は巡回ルート（=出発点に戻る）とみなす
• end が指定されている場合は片道ルート（=出発点と異なる場所で終了）とする

実装例

def nearest_neighbor_extended(D, start=0, end=None):
    n = len(D)
    assert 0 <= start < n, "start が範囲外です"
    if end is not None:
        assert 0 <= end < n, "end が範囲外です"

    unvisited = set(range(n))
    unvisited.discard(start)
    if end is not None:
        unvisited.discard(end)

    route = [start]
    current = start

    while unvisited:
        next_city = min(unvisited, key=lambda j: D[current][j])
        unvisited.remove(next_city)
        route.append(next_city)
        current = next_city

    # 巡回ルートなら出発点に戻る
    if end is None:
        route.append(start)
    else:
        route.append(end)

    return route

5. 2-opt 改善法 の拡張

巡回ルートの場合

従来どおり、ルート全体を対象にして2本の辺を入れ替え、
より短い経路が得られれば改善を繰り返します。

片道ルートの場合

始点と終点は固定されるため、
両端を固定したまま中間部分だけを2-optの対象とします。

実装例

def two_opt_extended(route, D, is_cycle=True):
    best = route[:]
    n = len(best)
    if n < 4:
        return best

    improved = True
    while improved:
        improved = False
        # 巡回の場合は全体を対象、片道の場合は両端を除外
        start_idx = 1
        end_idx = n - 2 if not is_cycle else n - 1

        for i in range(start_idx, end_idx - 1):
            for j in range(i + 1, end_idx):
                if j - i == 1:  # 隣接区間はスキップ
                    continue
                new_route = best[:i] + best[i:j][::-1] + best[j:]
                if total_distance(D, new_route) < total_distance(D, best):
                    best = new_route
                    improved = True
    return best

6. 実行例と結果比較

ここでは、前回と同じ東京都内のスポットを対象に、
巡回ルートと片道ルートの両方を計算して比較してみます。

スクリプト全体

import math

# -----------------------------
# サンプルデータ（東京都内のスポット）
# -----------------------------
places = [
    ("東京駅",         35.681236, 139.767125),
    ("浅草寺",         35.714765, 139.796655),
    ("東京スカイツリー", 35.710063, 139.810700),
    ("上野公園",       35.714167, 139.774444),
    ("渋谷駅",         35.658034, 139.701636),
]

# -----------------------------
# 距離計算（ハーサイン：km）
# -----------------------------
def haversine(lat1, lon1, lat2, lon2) -> float:
    """2地点間の大円距離を km 単位で返す。"""
    R = 6371.0
    phi1, phi2 = math.radians(lat1), math.radians(lat2)
    dphi = math.radians(lat2 - lat1)
    dlmb = math.radians(lon2 - lon1)
    a = math.sin(dphi / 2) ** 2 + math.cos(phi1) * math.cos(phi2) * math.sin(dlmb / 2) ** 2
    return 2 * R * math.asin(math.sqrt(a))

def build_distance_matrix(places):
    """対称行列の性質を使って計算を半分に。単位は km。"""
    n = len(places)
    D = [[0.0]*n for _ in range(n)]
    for i in range(n):
        for j in range(i+1, n):
            d = haversine(places[i][1], places[i][2], places[j][1], places[j][2])
            D[i][j] = D[j][i] = d
    return D

def total_distance(D, route) -> float:
    """route は都市インデックスの並び。最後の要素は到着点（巡回なら開始点と同じ）。"""
    return sum(D[route[i]][route[i+1]] for i in range(len(route)-1))

# -----------------------------
# 拡張版 最近近傍法（巡回/片道対応）
# -----------------------------
def nearest_neighbor_extended(D, start=0, end=None):
    """
    - 巡回: end=None のとき、最後に start に戻る
    - 片道: end が指定されているとき、最後は end で終了（end は訪問対象から事前に除外）
    """
    n = len(D)
    assert 0 <= start < n, "start が範囲外です"
    if end is not None:
        assert 0 <= end < n, "end が範囲外です"

    unvisited = set(range(n))
    unvisited.discard(start)
    if end is not None:
        unvisited.discard(end)

    route = [start]
    current = start

    while unvisited:
        nxt = min(unvisited, key=lambda j: D[current][j])
        unvisited.remove(nxt)
        route.append(nxt)
        current = nxt

    # 巡回/片道の終点処理
    if end is None:
        route.append(start)
    else:
        route.append(end)

    return route

# -----------------------------
# 拡張版 2-opt（巡回/片道対応）
# -----------------------------
def two_opt_extended(route, D, is_cycle=True):
    """
    - 巡回: ルート全体を対象に 2-opt 改善（閉路想定、最後は開始点）
    - 片道: 始点・終点は固定し、間の区間のみ対象に 2-opt 改善
    """
    best = route[:]  # 参照共有を避ける
    n = len(best)
    if n < 4:
        return best

    improved = True
    while improved:
        improved = False
        if is_cycle:
            # 例: [s, ..., s] の閉路（末尾は開始点と同じ index）
            # 端点（0/-1）は固定扱いとし、中間だけ反転候補にする
            i_start, i_end_excl = 1, n-1   # i in [1, n-2]
            j_end_excl = n-1               # j in (i+1, n-2]
        else:
            # 片道: 両端(0, n-1)固定で中間のみ
            i_start, i_end_excl = 1, n-2   # i in [1, n-3]
            j_end_excl = n-1               # j in (i+1, n-2]

        for i in range(i_start, i_end_excl):
            for j in range(i+1, j_end_excl):
                if j - i == 1:  # 隣接区間の反転は効果薄なのでスキップ
                    continue
                new_route = best[:i] + best[i:j][::-1] + best[j:]
                if total_distance(D, new_route) < total_distance(D, best):
                    best = new_route
                    improved = True
    return best

# -----------------------------
# ユーティリティ
# -----------------------------
def route_names(route, places):
    return [places[i][0] for i in route]

# -----------------------------
# デモ実行
# -----------------------------
if __name__ == "__main__":
    D = build_distance_matrix(places)

    # 巡回ルート（東京駅→東京駅）
    route_cycle_nn  = nearest_neighbor_extended(D, start=0, end=None)
    route_cycle_opt = two_opt_extended(route_cycle_nn, D, is_cycle=True)
    dist_cycle_nn   = total_distance(D, route_cycle_nn)
    dist_cycle_opt  = total_distance(D, route_cycle_opt)

    print("【巡回】NN（インデックス） :", route_cycle_nn)
    print("【巡回】NN（名称）         :", " -> ".join(route_names(route_cycle_nn, places)))
    print(f"【巡回】総距離 NN         : {dist_cycle_nn:.2f} km")
    print("【巡回】2-opt（インデックス）:", route_cycle_opt)
    print("【巡回】2-opt（名称）       :", " -> ".join(route_names(route_cycle_opt, places)))
    print(f"【巡回】総距離 2-opt      : {dist_cycle_opt:.2f} km")
    print("-"*60)

    # 片道ルート（東京駅→渋谷駅）
    route_one_nn  = nearest_neighbor_extended(D, start=0, end=4)
    route_one_opt = two_opt_extended(route_one_nn, D, is_cycle=False)
    dist_one_nn   = total_distance(D, route_one_nn)
    dist_one_opt  = total_distance(D, route_one_opt)

    print("【片道】NN（インデックス） :", route_one_nn)
    print("【片道】NN（名称）         :", " -> ".join(route_names(route_one_nn, places)))
    print(f"【片道】総距離 NN         : {dist_one_nn:.2f} km")
    print("【片道】2-opt（インデックス）:", route_one_opt)
    print("【片道】2-opt（名称）       :", " -> ".join(route_names(route_one_opt, places)))
    print(f"【片道】総距離 2-opt      : {dist_one_opt:.2f} km")

# -----------------------------------------------------------------------------
# 【巡回】NN（インデックス） : [0, 3, 1, 2, 4, 0]
# 【巡回】NN（名称）         : 東京駅 -> 上野公園 -> 浅草寺 -> 東京スカイツリー -> 渋谷駅 -> 東京駅
# 【巡回】総距離 NN         : 24.98 km
# 【巡回】2-opt（インデックス）: [0, 2, 1, 3, 4, 0]
# 【巡回】2-opt（名称）       : 東京駅 -> 東京スカイツリー -> 浅草寺 -> 上野公園 -> 渋谷駅 -> 東京駅
# 【巡回】総距離 2-opt      : 23.97 km
# ------------------------------------------------------------
# 【片道】NN（インデックス） : [0, 3, 1, 2, 4]
# 【片道】NN（名称）         : 東京駅 -> 上野公園 -> 浅草寺 -> 東京スカイツリー -> 渋谷駅
# 【片道】総距離 NN         : 18.52 km
# 【片道】2-opt（インデックス）: [0, 3, 1, 2, 4]
# 【片道】2-opt（名称）       : 東京駅 -> 上野公園 -> 浅草寺 -> 東京スカイツリー -> 渋谷駅
# 【片道】総距離 2-opt      : 18.52 km
# -----------------------------------------------------------------------------

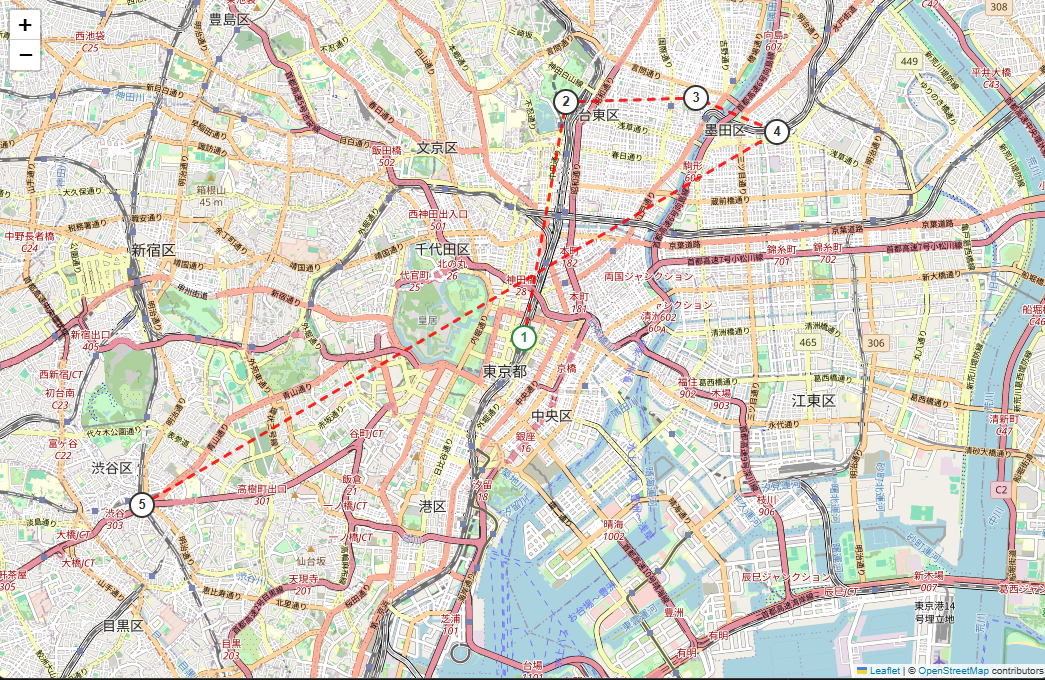
folium で可視化

import folium

def plot_route_numbered(places, route, filename="route.html", color="blue", is_cycle=True):
    """
    1本のルートを番号付きで可視化してHTML保存する。
    - is_cycle=True なら閉路（最後に開始点へ戻る線を描く）
    - is_cycle=False なら片道（線は閉じない、点線で描く）
    """
    start_idx = route[0]
    center = [places[start_idx][1], places[start_idx][2]]
    m = folium.Map(location=center, zoom_start=13)

    def to_latlons(r):
        return [(places[i][1], places[i][2]) for i in r]

    latlons = to_latlons(route)

    # 巡回のみ線を閉じる
    if is_cycle:
        if route[-1] != route[0]:
            latlons.append((places[start_idx][1], places[start_idx][2]))
        poly_kwargs = dict(weight=3, opacity=0.85, color=color)
    else:
        # 片道は閉じない＆点線で視覚差
        poly_kwargs = dict(weight=3, opacity=0.85, color=color, dash_array="6,8")

    folium.PolyLine(latlons, **poly_kwargs).add_to(m)

    # 訪問順ラベル（巡回は最後の重複を除く）
    seq = route[:-1] if (is_cycle and route[-1] == route[0]) else route[:]

    for order, idx in enumerate(seq, start=1):
        name, lat, lon = places[idx]
        badge = f"""
        <div style="
            background:white; border: 2px solid {'#2b8a3e' if order==1 else '#333'};
            color: {'#2b8a3e' if order==1 else '#333'};
            width: 26px; height: 26px; line-height: 22px;
            text-align: center; font-weight: 700;
            border-radius: 50%; font-size: 13px;">
            {order}
        </div>"""
        icon = folium.DivIcon(html=badge, icon_size=(26,26), icon_anchor=(13,13))
        popup_html = f'<div style="white-space:nowrap;word-break:keep-all;font-size:14px;">{order}: {name}</div>'
        folium.Marker(
            location=[lat, lon],
            icon=icon,
            popup=folium.Popup(popup_html, max_width=400),
            tooltip=folium.Tooltip(f"{order}: {name}", sticky=True)
        ).add_to(m)

    # 始点/終点の強調
    start_lat, start_lon = places[start_idx][1], places[start_idx][2]
    folium.CircleMarker([start_lat, start_lon], radius=8, fill=True, fill_opacity=0.7,
                        color="#2b8a3e", fill_color="#2b8a3e", popup="START").add_to(m)
    end_idx = seq[-1]
    end_lat, end_lon = places[end_idx][1], places[end_idx][2]
    folium.CircleMarker([end_lat, end_lon], radius=7, fill=True, fill_opacity=0.7,
                        color="#c92a2a", fill_color="#c92a2a",
                        popup="END" if end_idx != start_idx else "END (=START)").add_to(m)

    m.save(filename)
    return filename

始点：東京駅／終点：渋谷駅

7. まとめ

本記事では、複数地点を効率よく回る経路を求める 巡回経路探索（TSP） を Python で実装し、次のポイントを確認しました。

• 始点・終点を任意に指定できるよう拡張
• 巡回ルート（出発点に戻る）と 片道ルート（別の地点で終了）の両方に対応

今回の実装は基本的なものでしたが、さらに応用が可能です。
例えば、より多くの地点を対象にした場合の計算効率化や、道路に沿った距離・所要時間を用いた現実的なルート探索などが考えられます。