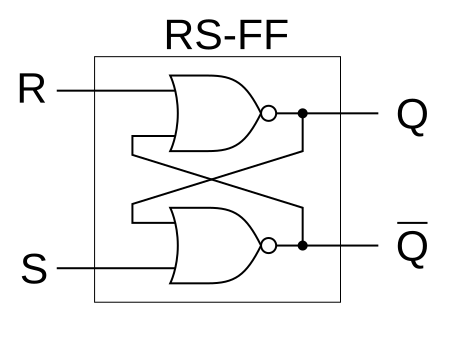
いわゆるRSフリップフロップについての小ネタです.
二つの入力SとR,二つの出力Qと~Qを持ち,出力が二つのNORゲートに互い違いにフィードバックされる,変わった論理回路です.
これの真理値表は
| S | R | Q | ~Q | |
|---|---|---|---|---|
| 0 | 0 | 保持 | ||
| 1 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 1 | 禁則 | ||
と紹介されることが多いです(たとえばWikipedia).
- (S,R)=(1,0)とするとQは1となる(Set操作)
- (S,R)=(0,1)とするとQは0となる(Reset操作)
- (S,R)=(0,0)とすると,Qが0と1のどちらであってもそれが保持される(記憶操作)
- (S,R)=(1,1)としてはいけない(禁則操作)
ということで,記憶するという機能を持ちます.RSフリップフロップはDRAMやレジスタの最小構成要素です.
この記事は,上の表を見て「ん?NORゲートの入力は,SとRの他に出力Q,~Qもあるんだから,真理値表は2^4=16通りのパターンがあるはずじゃないの?」「ていうか禁則って何だよ?」と疑問を持った方のためのものです.
16通りのパターンを書き下してみましょう.
| S | R | 一つ前の | 新しい | |||
|---|---|---|---|---|---|---|
| Q | ~Q | Q | ~Q | |||
| 0 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 0 | |||
| 0 | 1 | 0 | 1 | |||
| 1 | 1 | 0 | 0 | |||
| 1 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 0 | |||
| 0 | 1 | 1 | 1 | |||
| 1 | 1 | 1 | 0 | |||
| 0 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 1 | |||
| 0 | 1 | 0 | 1 | |||
| 1 | 1 | 0 | 1 | |||
| 1 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 1 | |||
| 0 | 1 | 1 | 1 | |||
| 1 | 1 | 1 | 1 | |||
(S,R)=(0,0)のとき,(Q,~Q)=(0,0)なら次の瞬間に(Q,~Q)=(1,1)となります.また(Q,~Q)=(1,1)なら次の瞬間に(Q,~Q)=(0,0)となります.つまり,ある瞬間に(Q,~Q)=(0,0)または(1,1)となってしまったら,その後は(0,0)と(1,1)がめまぐるしく入れ替わることになります(表中の赤字).
一方,(Q,~Q)=(1,0)ならその後もずっと(1,0),(Q,~Q)=(0,1)ならその後もずっと(0,1)であり続けることも分かります.
(S,R)=(1,0)のとき,(Q,~Q)=(0,0)または(0,1)なら次の瞬間には(1,1)となります.また,(Q,~Q)=(1,1)ならば次の瞬間に(1,0)となります.(Q,~Q)=(1,0)ならば次も(1,0)なので,つまりこの場合,(Q,~Q)の初期値が何であっても時間が経てば(1,0)に収束することになります(表中の青字).
逆に(S,R)=(0,1)のときは,全く同様の考察によって,(Q,~Q)の初期値が何であっても時間が経てば(0,1)に収束すると分かります(表中の青字).
(R,S)=(1,1)のとき,(Q,~Q)の初期状態が何であっても次の瞬間には(Q,~Q)=(1,1)となり,その後もずっと(1,1)であり続けます(表中の青字).
以上をまとめると,
- (S,R)=(1,0)なら(Q,~Q)=(1,0)に収束する.
- (S,R)=(0,1)なら(Q,~Q)=(0,1)に収束する.
- (Q,~Q)=(1,0)または(0,1)の状態で(S,R)=(0,0)とすると,どちらにしても(Q,~Q)の状態が保存(記憶)される.
- (S,R)=(1,1)とすると(Q,~Q)=(1,1)となる。この状態で仮にS,Rを同時に(S,R)=(0,0)と変えると,(Q,~Q)の値はめまぐるしく変わり収束しない.したがって(S,R)=(1,1)としてはいけない(禁則操作).
ということが言えます.禁則操作は,それ自体が問題なのではなく,それによって記憶を意図した操作の結果が不定になりかねないことが問題だったというわけです.
最初に示した真理値表は,最後の結論だけをまとめたものだったということも,これでお分かり頂けると思います.
禁則を定めた下では,~Qは必ずQの反転値となります.そもそも~Qと書いているのは,これが理由です.