はじめに
最近たまたまこの話題が複数箇所で挙がったので,自分の考えを整理しておきます.
いろいろ調べて分かったことですが,3次元姿勢表現に関する話はかなり混乱しており,不注意な説明をしている書籍・資料も多いです.それがまた混乱を助長しているようにも思います.ただ,混乱が生じるのも致し方なしと思える理由もあります.本記事から,そのあたりを感じとって頂けたら幸いです.
ロール・ピッチ・ヨーに関する混乱を解くためには,まずオイラー角を理解しなければいけません.もう理解している,という方は,次の節は読み飛ばしていきなり本題に入って頂いて大丈夫です.
姿勢表現にまつわる基本的な話
姿勢って何だろう
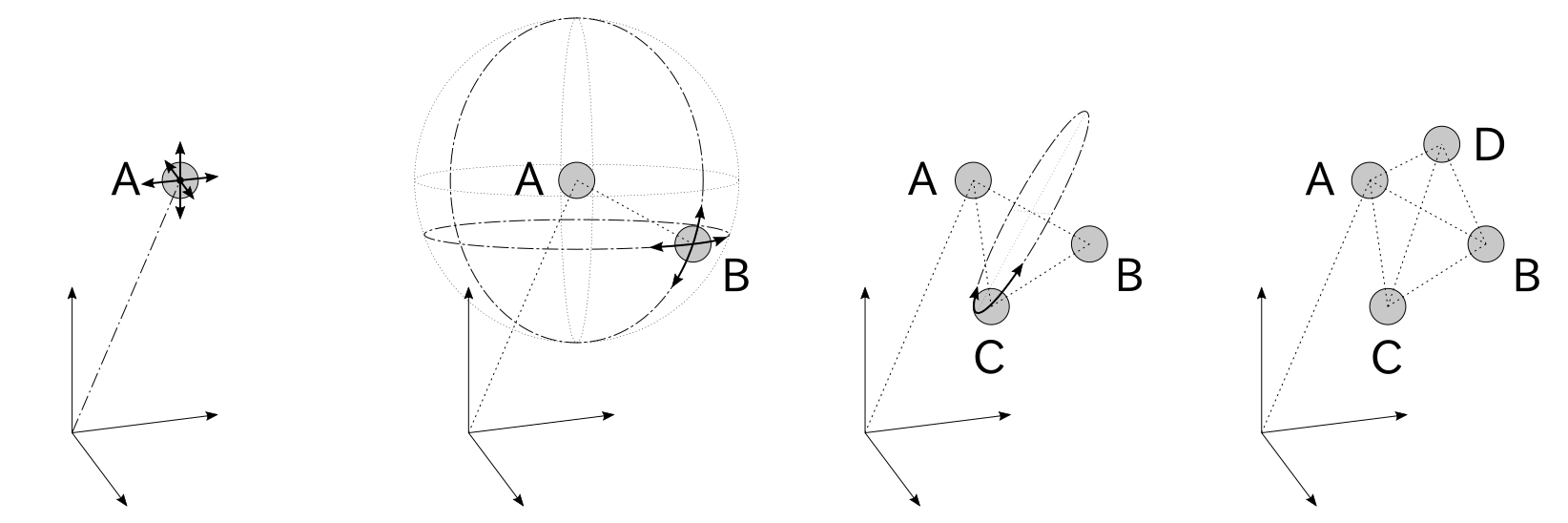
変形しない物体(剛体)が3次元空間でどのような配位をとり得るか?が3次元姿勢表現に関わる大元の問いです.変形しないとは,その物体を構成する無数の点群が互いに距離を保つということです.その無数の点から一点Aを選んで,空間における位置を定めましょう.よく知られている通り,位置は3つの数字(たとえばデカルト座標系における縦・横・高さ)によって一意に決まります.
その状況で,さらにもう一点Bを選びましょう.点Bは点Aから距離を一定に保ちながら動くことができます.このような点の集合は,点Aを中心とする球面を描きます.球面上の点の位置は,2つの数字(たとえば緯度・経度)によって一意に決まります.
さらにもう一点Cを選びます.三角形ABCは,点Aと点Bを通る直線を軸として回転できます.このとき点Cは,その軸まわりに円を描きます.円上の点の位置は,1つの数字(偏位角)によって一意に決まります.
これらの3点の位置が決まった時点で,他の全ての点の位置も同時に決まります.よって,剛体のとり得る配位は3+2+1=6個の数字が与えられれば一意に決まると分かります.最初の3個は,剛体を平行移動(並進)させるもの,あとの3個は,点Aまわりに剛体を回転させるものと考えても良いです.前者の並進によって決まる配位を剛体の位置と呼ぶのは自然でしょう.剛体の姿勢とは,後者の回転によって決まる配位のことです.
物体座標系
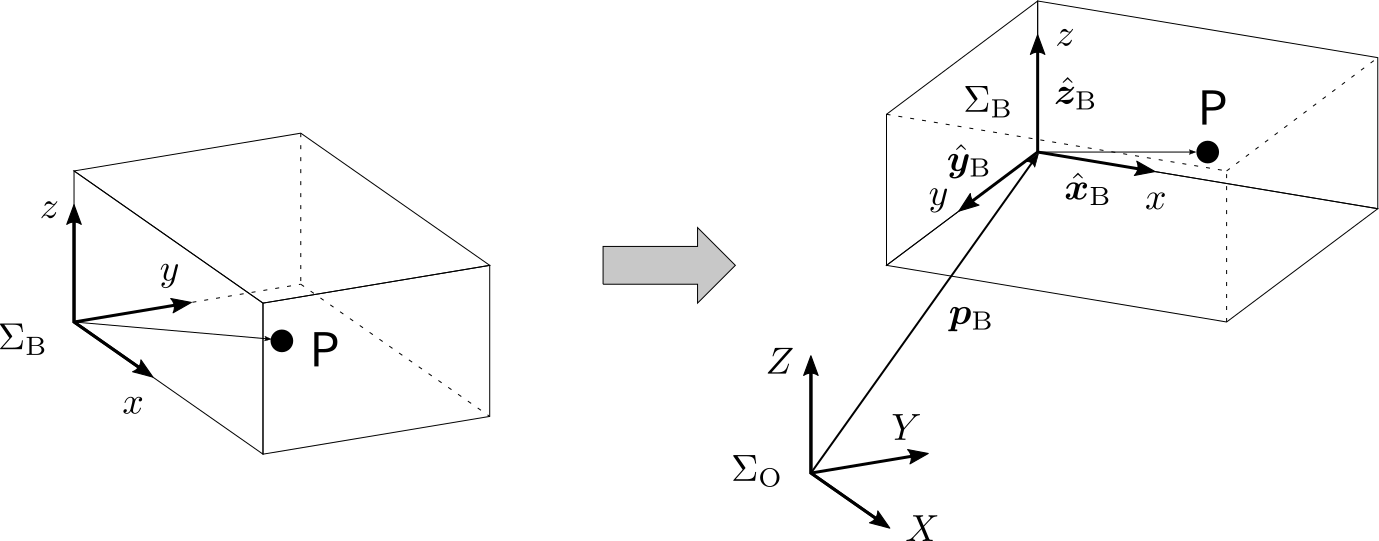
剛体が,上図のような直方体であるとしましょう.直方体の頂点の一つを原点とし,その頂点に隣接する3本の稜線それぞれに沿って$x$,$y$,$z$軸を設け,座標系$\Sigma_{\mathrm{B}}$とします.このとき,物体上の任意の点Pはこの座標系(物体座標系)$\Sigma_{\mathrm{B}}$における定点となります.
一般的には,原点が物体の頂点である必要はありませんし,座標軸も物体の稜線に沿っている必要はないのですが,分かりやすさのためこうします.
この直方体を他の座標系$\Sigma_{\mathrm{O}}$から見ることを考えます.$\Sigma_{\mathrm{B}}$における点Pの位置ベクトルが${}^{\mathrm{B}}\boldsymbol{p}=[x~y~z]^{\mathrm{T}}$であるとき,同じ点の$\Sigma_{\mathrm{O}}$における座標$\boldsymbol{p}=[X~Y~Z]^{\mathrm{T}}$は次のように計算できます.
\boldsymbol{p}=\boldsymbol{p}_{\mathrm{B}}+x\hat{\boldsymbol{x}}_{\mathrm{B}}+y\hat{\boldsymbol{y}}_{\mathrm{B}}+z\hat{\boldsymbol{z}}_{\mathrm{B}}
ただし,$\boldsymbol{p}_{\mathrm{B}}$は$\Sigma_{\mathrm{O}}$における$\Sigma_{\mathrm{B}}$原点の位置ベクトル,$\hat{\boldsymbol{x}}_{\mathrm{B}}$,$\hat{\boldsymbol{y}}_{\mathrm{B}}$,および$\hat{\boldsymbol{z}}_{\mathrm{B}}$はそれぞれ
$\Sigma_{\mathrm{O}}$における$\Sigma_{\mathrm{B}}$の$x$,$y$,$z$軸の単位方向ベクトルです.
これは次のようにまとめることもできます.
\boldsymbol{p}=\boldsymbol{p}_{\mathrm{B}}+\boldsymbol{R}_{\mathrm{B}}{}^{\mathrm{B}}\boldsymbol{p}
ただし,$\boldsymbol{R}_{\mathrm{B}}$は$\hat{\boldsymbol{x}}_{\mathrm{B}}$,$\hat{\boldsymbol{y}}_{\mathrm{B}}$,$\hat{\boldsymbol{z}}_{\mathrm{B}}$を基底とする次の行列です.
\boldsymbol{R}_{\mathrm{B}}
=\begin{bmatrix} \hat{\boldsymbol{x}}_{\mathrm{B}} & \hat{\boldsymbol{y}}_{\mathrm{B}} & \hat{\boldsymbol{z}}_{\mathrm{B}} \end{bmatrix}
この$\boldsymbol{p}_{\mathrm{B}}$と$\boldsymbol{R}_{\mathrm{B}}$の組が,剛体の配位を決定する本質的な量で,それぞれ位置と姿勢に対応します.本記事の関心事項は姿勢なので,以降は$\boldsymbol{R}_{\mathrm{B}}$に焦点を置きます.
姿勢行列
$\boldsymbol{R}_{\mathrm{B}}$は姿勢行列と呼ばれます.上の式から分かる通り,これは$3\times 3$正方行列です.$\boldsymbol{R}_{\mathrm{B}}$の中身である$\hat{\boldsymbol{x}}_{\mathrm{B}}$,$\hat{\boldsymbol{y}}_{\mathrm{B}}$,および$\hat{\boldsymbol{z}}_{\mathrm{B}}$は互いに直交する単位ベクトルですから,次式を満たします.
\displaylines{
\hat{\boldsymbol{x}}_{\mathrm{B}}^{\mathrm{T}}
\hat{\boldsymbol{x}}_{\mathrm{B}}
=
\hat{\boldsymbol{y}}_{\mathrm{B}}^{\mathrm{T}}
\hat{\boldsymbol{y}}_{\mathrm{B}}
=
\hat{\boldsymbol{z}}_{\mathrm{B}}^{\mathrm{T}}
\hat{\boldsymbol{z}}_{\mathrm{B}}
=1
\\
\hat{\boldsymbol{x}}_{\mathrm{B}}^{\mathrm{T}}
\hat{\boldsymbol{y}}_{\mathrm{B}}
=
\hat{\boldsymbol{y}}_{\mathrm{B}}^{\mathrm{T}}
\hat{\boldsymbol{z}}_{\mathrm{B}}
=
\hat{\boldsymbol{z}}_{\mathrm{B}}^{\mathrm{T}}
\hat{\boldsymbol{x}}_{\mathrm{B}}
=0
}
これより,次式が成り立つと分かります.
\boldsymbol{R}_{\mathrm{B}}^{\mathrm{T}}\boldsymbol{R}_{\mathrm{B}}=\boldsymbol{1}
ただし,$\boldsymbol{1}$は単位行列です.つまり,$\boldsymbol{R}_{\mathrm{B}}$は転置をとれば逆行列になるということです.このような行列を正規直交行列と呼びます.
正規直交行列は$3\times 3=9$個の成分を持ちますが,各成分間には上記の6本の等式拘束条件が課されますので,独立に決められるのは3個だけです.これは先に述べた,「姿勢は3つの数字で表すことができる」ということと整合します.
ところで,直交座標系には右手系と左手系が存在します.姿勢とは回転によって決まる配位,と説明しました.任意の右手系を回転させて得られる姿勢は必ず右手系になりますし,左手系についても然りです.したがって,座標変換として並進と回転によるもののみを扱う場合,右手系と左手系を混在させることは混乱の元となります.
外積をきちんと定義してやれば混乱は防げるのですが,本記事ではそのことはスコープには含めず,座標系は全て右手系の直交座標系であるとしましょう.このことを保証するには,上の6本の等式拘束条件を次の拘束条件で置き換える必要があります.
\displaylines{
\hat{\boldsymbol{x}}_{\mathrm{B}}
\times
\hat{\boldsymbol{y}}_{\mathrm{B}}
=
\hat{\boldsymbol{z}}_{\mathrm{B}}
\\
\hat{\boldsymbol{y}}_{\mathrm{B}}
\times
\hat{\boldsymbol{z}}_{\mathrm{B}}
=
\hat{\boldsymbol{x}}_{\mathrm{B}}
\\
\hat{\boldsymbol{z}}_{\mathrm{B}}
\times
\hat{\boldsymbol{x}}_{\mathrm{B}}
=
\hat{\boldsymbol{y}}_{\mathrm{B}}
}
これは見た目上9本の等式拘束条件ですが,互いに独立な式は6本しかありません.よって,「姿勢は3つの数字で定めることができる」という結論に変わりはありません.
オイラー角
座標系の姿勢を定める3つの数字の選び方には様々なものがありますが,それらの中で最もよく知られているのはオイラー角でしょう.これはある座標系を,その座標軸のうちある1本のまわりに$\alpha$回転,次いでそれと異なる1本のまわりに$\beta$回転,さらにそれと異なる1本のまわりに$\gamma$回転させることで,別の座標系に変換する手続きを考えたときの,$(\alpha, \beta, \gamma)$のことです.
このような軸の選び方は$3\times 2\times 2=12$通りありますので,たとえば$z$軸,$y$軸,$x$軸の順に選んだならば$z$-$y$-$x$オイラー角などと呼んでそれが分かるようにします.
下は,$z$-$y$-$x$オイラー角で姿勢が表される座標系を図示したものです.
具体的には,$\boldsymbol{R}_{\mathrm{B}}$次のように計算できます.
\displaylines{
\boldsymbol{R}_{\mathrm{B}}&=
\begin{bmatrix}
\cos\alpha & -\sin\alpha & 0 \\
\sin\alpha & \cos\alpha & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos\beta & 0 & \sin\beta \\
0 & 1 & 0 \\
-\sin\beta & 0 & \cos\beta
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\gamma & -\sin\gamma \\
0 & \sin\gamma & \cos\gamma
\end{bmatrix} \\
&=\begin{bmatrix}
C_{\alpha}C_{\beta} & C_{\alpha}S_{\beta}S_{\gamma}-S_{\alpha}C_{\gamma} & C_{\alpha}S_{\beta}C_{\gamma}+S_{\alpha}S_{\gamma} \\
S_{\alpha}C_{\beta} & S_{\alpha}S_{\beta}S_{\gamma}+C_{\alpha}C_{\gamma} & S_{\alpha}S_{\beta}C_{\gamma}-C_{\alpha}S_{\gamma} \\
-S_{\beta} & C_{\beta}S_{\gamma} & C_{\beta}C_{\gamma}
\end{bmatrix}
}
ただし,$S_{\alpha}\overset{\mathrm{def}}{=}\sin\alpha$,$C_{\alpha}\overset{\mathrm{def}}{=}\cos\alpha$,$S_{\beta}\overset{\mathrm{def}}{=}\sin\beta$,$C_{\beta}\overset{\mathrm{def}}{=}\cos\beta$,$S_{\gamma}\overset{\mathrm{def}}{=}\sin\gamma$,$C_{\gamma}\overset{\mathrm{def}}{=}\cos\gamma$とそれぞれおきました.
オイラー角によって任意の姿勢を表現できることは,次のように任意の正規直交行列$\boldsymbol{R}$からオイラー角$(\alpha,\beta,\gamma)$を逆算できる,という事実によって示されます.
\displaylines{
\alpha=\begin{cases}
\mathop{\mathrm{atan2}}(r_{21},r_{11}) & \\
\mathop{\mathrm{atan2}}(r_{21},r_{11})\pm\pi & (\mbox{ただし複号は$-\pi<\alpha\leq\pi$を満たすように決定する})
\end{cases} \\
\beta=\mathop{\mathrm{atan2}}(-r_{31},r_{11}C_{\alpha}+r_{21}S_{\alpha}) \\
\gamma=\mathop{\mathrm{atan2}}(r_{13}S_{\alpha}-r_{23}C_{\alpha},-r_{12}S_{\alpha}+r_{22}C_{\alpha})
}
ただし,$\boldsymbol{R}$の成分を次のようにおきました.
\boldsymbol{R}=\begin{bmatrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{bmatrix}
また,$\theta=\mathop{\mathrm{atan2}}(y,x)$は点$(x,y)$の偏角$\theta$を$-\pi<\theta\leq\pi$の範囲で返す逆正接関数であり,コンピュータを用いて計算を行う場合,大抵の算術ライブラリに組み込み関数として用意されています.
なお,$\beta=\pm\frac{\pi}{2}$のとき,$r_{11}=r_{21}=0$となります.$\mathop{\mathrm{atan2}}(0,0)$は未定義であるため,$\alpha$を一意に求めることができません.このような現象はジンバルロックと呼ばれます.また,ジンバルロックを起こす姿勢は特異点と呼ばれます.
上記に示したのは$z$-$y$-$x$オイラー角の例のみですが,どのオイラー角も一般的には任意の姿勢行列$\boldsymbol{R}$から(復号を伴う形で二つ)逆算することができますし,特異点も必ず存在しますがオイラー角自体が存在しないことはありません.
姿勢行列もオイラー角も様々な数理に満ちており,それだけで1冊本が書けるほどですが,本記事の主題ではないので割愛します.
移動体の姿勢と回転運動
オイラー角は,任意の物体(剛体)の姿勢を表すためのものです.物体座標系は,原点が物体の頂点である必要も,座標軸が物体の稜線に沿っている必要もなく,右手系かつ直交座標系であるという最低限の仮定の下に,物体の形などと無関係に定めることができます.すなわち,物体座標系における3本の座標軸は特別な意味を持ちません.
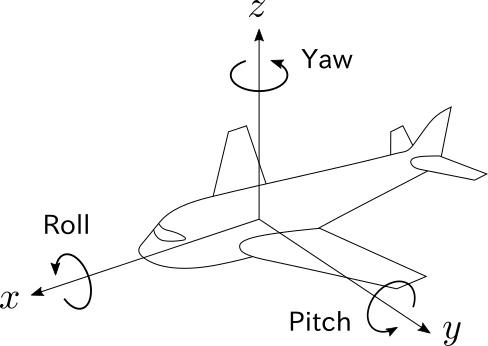
物体が移動体である場合には,少し話が変わってきます.移動体とは,「前」を持つ物体,と言い換えても良いでしょう.典型例は車輌,飛行機,船舶などです.機械工学の流儀では,前方向を$x$軸,上方向を$z$軸,左方向を$y$軸とします.座標軸がそれぞれ特別な意味を持つということです.そして,$x$(前後)軸まわりの回転をローリング,$y$(左右)軸まわりの回転をピッチング,$z$(上下)軸まわりの回転をヨーイングとそれぞれ呼びます.このことから,$x$(前後)軸をロール軸,$y$(左右)軸をピッチ軸,$z$(上下)軸をヨー軸と呼ぶこともしばしばあります.
ところで,「上」とはどの方向でしょう?多くの人は,重力に引かれる方向が「下」,その逆が「上」,と考えるのではないでしょうか?筆者自身もそう認識しています.ところがこの場合,重力の方向は身体と無関係に定まるものですので,「前」と直交する保証は全くありません.それどころか,同一軸になってしまうこともあり得ます(仰向けに寝転がった状況を想像して下さい).これでは,上に書いた「前方向を$x$軸,上方向を$z$軸」つまり互いに直交する2軸と見なすことと,数学的に矛盾してしまいます.
あるいは移動体を自分の身体に重ね合わせて,頭のある方が「上」,という人もいるかも知れません.移動体の「頭」をどう決めるのかという問題はありますが,それは人工物の設計の問題なので,身体を基準に人為的に定義するという意味だと理解して頂ければ良いでしょう.「前方向を$x$軸,上方向を$z$軸」という表現が数学的に矛盾しないので,これはこれで合理的な決め方です.一方,逆立ちしたら地面が上になる,ということに違和感を覚える人もいることでしょう.
移動体の姿勢を表す時に慣習的に用いられる「上下」は,「移動体は近似的に水平面内を動く,よって身体基準の『上』と重力基準の『上』は近似的に一致する」という暗黙の仮定の下に見出されたもので,数学的にはことほど左様に曖昧なものである,ということをご理解頂けたでしょうか.
余談ですが,「3次元姿勢」の意味での「姿勢」の英語訳としては「attitude」と「orientation」が知られています.筆者の感覚では,「orient」は「向く」という動詞ですので,暗に前を持つもの,すなわち移動体に適用される言葉です.したがって「orientation」は移動体に限定した場合の姿勢で,任意の物体の姿勢を意味する場合には「attitude」を使う方が適当だと考えます.
z-y-xオイラー角をロール・ピッチ・ヨーと呼ぶのは間違っている
$z$-$y$-$x$オイラー角の$\alpha$をヨー角,$\beta$をピッチ角,$\gamma$をロール角とそれぞれ呼び,これをして「$z$-$y$-$x$オイラー角による姿勢表現をロール・ピッチ・ヨーとも呼ぶ」と説明している文献が相当数あります.しかし,幾つかの理由によってこれは間違いだと断言できます.
まず,前節冒頭に書いた通りオイラー角は任意の物体の姿勢を表すもので,前後・左右・上下の概念と無関係のものです.基準とする座標系も任意にとることができます.この時点で,ロール・ピッチ・ヨーという呼び方は馴染みません.
次に,前述の通りロール・ピッチ・ヨーは互いに直交する軸です.オイラー角の3本の回転軸は一般的には直交しませんので,この理由でも間違いです.そして,回転軸が互いに直交するということは,移動体の物体座標系における軸まわりの回転に限定した表現だということも同時に分かります.基準となる座標系が移動体自身とともに常に動くならば,この回転の角度を定義することはできません.剛体運動にある程度なじみのある方には,つまりこれは角速度のことなので,一般的には積分が意味を持たない,と説明すればお分かり頂けるでしょうか.
ちなみに,重力方向に沿って$z$軸を設けた慣性座標系を基準とする「移動体の姿勢」を$z$-$y$-$x$オイラー角で表したとき,$\alpha$を機首方位角(ベアリング角),$\beta$をピッチ角,$\gamma$をバンク角とそれぞれ呼ぶことが,慣習としてあります.「ピッチ角」だけロール・ピッチ・ヨーのピッチと対応しています.これは,上記の表現においては$\alpha$の回転軸と$\beta$の回転軸が常に直交し,$\beta$は水平面に対する仰角であることが保証されるからです.角速度のピッチ成分の積分が意味を持つ特殊な条件,と言っても良いでしょう.もっとも,そうして得られた「ピッチ角」は最終的な姿勢における$y$(左右)軸まわりの回転と一般的には対応していないし,混乱を招くので「仰角」と呼び替える方が良いのでは,と筆者個人は考えます.
ロボットの関節軸にロール・ピッチ・ヨーの名を当てるのは間違っている
ロボットの分野では,もう一つ混乱があります.それは,剛体の姿勢表現ではなく多関節ロボットの関節軸にロール・ピッチ・ヨーの名を当てる事例が少なからず見られるということです.
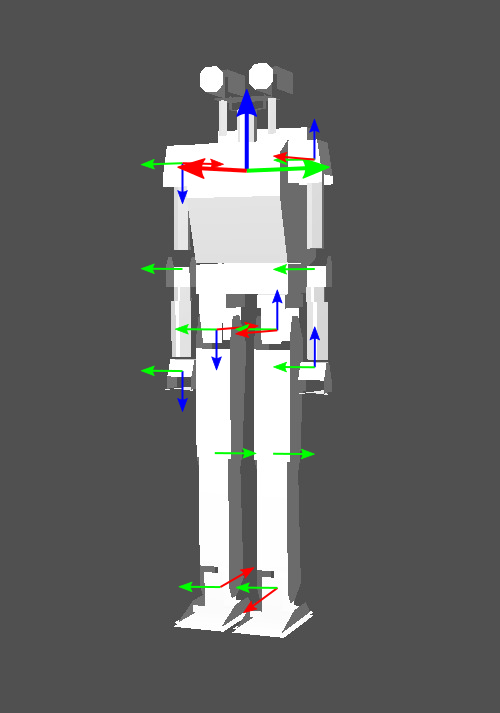
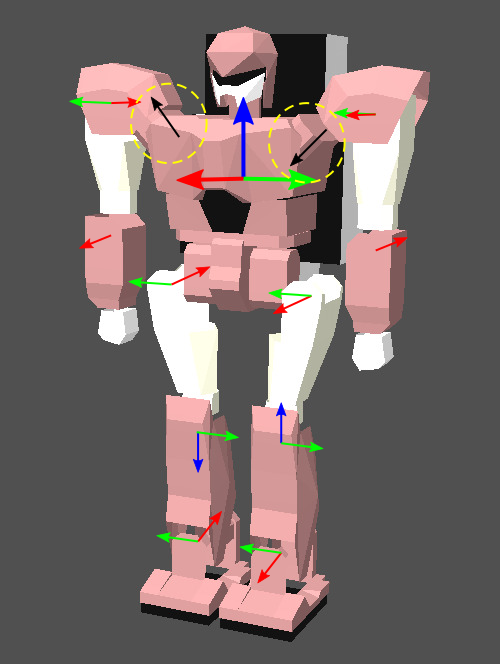
この用法を始めたのは,人型ロボットに関わる人たちではなかったかと思います(筆者自身,それに加担してしまった過去があることを白状しておきます).移動体としての人型ロボットは,身体の基準座標系(身体座標系,しばしば胴体に添えて設けられます)においてロール・ピッチ・ヨー軸を持ちます.たとえば下図のロボットの場合,胴体に記されている太めの赤矢印がロール軸,緑矢印がピッチ軸,青矢印がヨー軸です.そして直立時(基準姿勢)において,各関節軸(細めの赤緑青矢印)が胴体のロール軸・ピッチ軸・ヨー軸のいずれかに平行となる構成をとっています.図中,同じ色の矢印は互いに平行であることを意味しています.
ここで問題提起しているのは,赤矢印の関節軸をロール軸,緑矢印の関節軸をピッチ軸,青矢印の関節軸をヨー軸と呼ぶことの是非です.
関節軸の方向が身体にとってのロール・ピッチ・ヨーと一致しているこの基準姿勢において,そのような呼び方をするのは間違いとは言い切れないかも知れません.しかし,例えば上記のロボットの肘関節軸は基準姿勢においてはピッチ軸と平行ですが,腕を肩から90度横に開けば,同じ軸が今度はヨー軸と平行になります.ロボットのポーズ変化まで考えたときに,この呼び方は途端に怪しくなる,ということがこの例だけで分かるかと思います.
身体座標系が設けられている身体部位(上記の例ではどちらも胴体)に直結している関節軸(左右肩関節の1番目の軸と,左右股関節の1番目の軸)については,このようなことが起こらないので,特別にロール・ピッチ・ヨー軸のいずれかの呼び名を当てても良いのではないか?と考える方もいるかも知れません.
ですが,例えば下の図を見て下さい.
これは筆者が過去に作ったあるロボットのモデルですが,肩関節の1番目軸(破線で囲ったところ)が,基準姿勢において鉛直方向から45度傾いています.これはロール・ピッチ・ヨー軸いずれとも平行ではありません.
そもそもロボットの関節軸方向は隣接リンクに対して定まるもので,上記の例が示す通り,移動方向との直接的関係は一般的にはありません.よって,ロール・ピッチ・ヨーと呼び表すことは不適切だと言えます.
それでは何と呼ぶのが正しいのか?
ここは難しいところです.人型ロボットについては,人の解剖学と照らし合わせれば,「屈曲・伸展」「外転・内転」「外旋・内旋」「撓屈・尺屈」「背屈・底屈」などの呼び方が思いつきます.筆者も,習慣としてはこれらを採用することが多いです.ですがこれは,本来は軸の方向ではなく運動の方向に関する呼び名であり,両者は必ずしも一致しない(複数の軸まわりの回転が合成されてそれぞれの運動が生じ得る)ので,注意が必要です.
「任意のロボットの関節軸に関する,数学的に誤解を生じない命名規則は,(恐らく)存在しない」というのが筆者の見解です.
おわりに
車輌工学や船舶工学においては,「前方向を$x$軸,上方向を$z$軸,左方向を$y$軸とする」のが実態と乖離することは稀です.航空工学や宇宙工学においてはちょっと怪しくなります.「$z$-$y$-$x$オイラー角による姿勢表現をロール・ピッチ・ヨーとも呼ぶ」という間違った説明は,もしかしたら不注意な航空工学者が始めたのではと想像します.もっと不注意者が多いのがロボット工学者(過去の筆者自身を含め)です.
すでにある程度定着してしまった誤用を正すのはなかなか大変ですが,反省の念も込めつつ,努力は続けたいものです.