概要
"トグル・スイッチ力学系に関する線形安定性解析" という勉強ノートを作成しました.ノートは 本記事の最後 に置いてあります.
収録内容
- トグル・スイッチ力学系とは?
- 固定点 (平衡点) の計算
- 時間領域および周波数領域での線形安定性解析
- 作図に用いたpythonプログラム
はじめに
- トグル・スイッチ (toggle switch) 力学系は双安定性を有する力学系です
- この力学系は例えば,生物学分野の遺伝子発現モデルの一例として知られています
- 具体的には,遺伝子1と2が互いの発現を抑制する場合であり,遺伝子1が発現する (オン) と,遺伝子2が発現しにくくなる (オフ) ような機構のモデルとして使用されます
- ちょうどトグル・スイッチ (レバーでオン・オフを制御する装置) に似ていることが名前の由来らしいです
ノートのまとめ
■ 考える式系
\begin{align}
\frac{dp_{1}}{dt}&=\frac{\alpha}{1+p_{2}^{2}}-p_{1} \\
\frac{dp_{2}}{dt}&=\frac{\alpha}{1+p_{1}^{2}}-p_{2}
\end{align}
ここで,$p_{1}, p_{2}$は遺伝子1と2に含まれるたんぱく質の濃度 (発現量),$\alpha$は生成量に関するパラメータです.各式の右辺第一項は生成,第二項は分解を表します.生成に関する項は,相手の濃度が高い場合に小さくなるため,互いの発現を抑制する作用を持ちます.
■ 平衡点周りの安定性
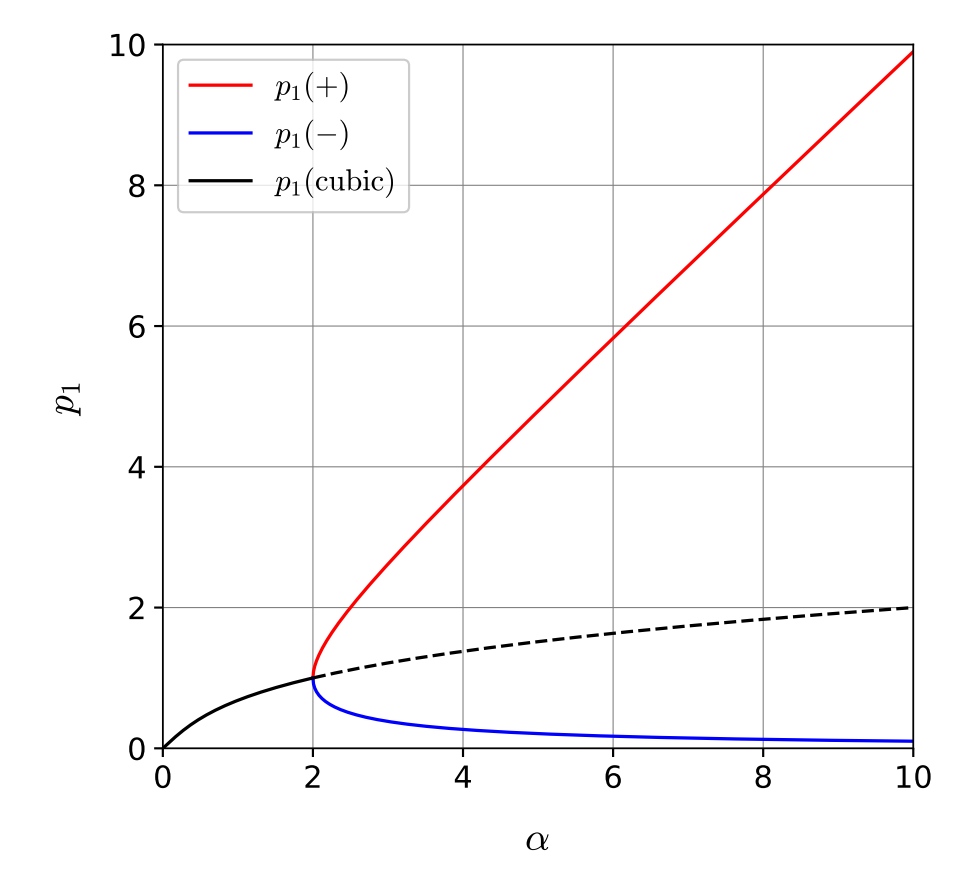
上式の平衡点 (定常解) を計算すると,以下の図のようになります (計算の詳細はノートをご参照ください).ただし,$p_{1}$は実数なので,図には実数解のみを描きました.$\alpha=2$を境にして,実数解が1つから3つに増えることが分かります.
それぞれの平衡点に関して線形安定性解析を行うことで,各平衡点が安定なのか不安定なのかを見ることができます.ただし,線形安定性解析では解くべき式を"線形化"しているため,平衡点に十分近い領域でのみ有効であることに注意してください.
下図のうち実線は安定な平衡点,破線は不安定な平衡点を表します.このような分岐はピッチフォーク分岐 (熊手型分岐) と呼ばれます.
詳しくはノートをご覧ください.
勉強ノート
勉強ノート (pdf) は以下に置きました.
内容に誤りを含む可能性がありますので,取り扱いにはご注意ください.