kaggleのHousePrices（住宅価格）に挑戦してみた。

はじめに

初めてkaggleに挑戦してみたので、その内容を記載していきたいと思います。
今回は、タイトルに記載したとおりHouse Prices - Advanced Regression Techniques
取り組みました。
初めての挑戦なので、一から自分で前処理をしてモデル構築するのは難しかったので、
kaggleのcodeを見たり、参考になる資料を真似てみたり、試行錯誤を繰り返しながら
モデルを構築して、提出してみました。
参考にさせていただいた記事
【Kaggle】「House Prices」をパクりながらやってみた。

結果はスコアが0.13947で順位は4205人中1616位でした。
参考記事ではモデルとしてLasso回帰を用いていました。
ただ、同じ回帰だと分析結果をみても、自分で挑戦したことにならないので、
Ridge回帰で分析を行って、スコアを出してみました。
何がスコアに影響があったのかと考えながら、分析していくことが大事だと思います。

記事の概要

House PriceのコンペでRidge回帰を使ってモデル構築を行います。

目次

1. House Pricesの概要
2. データの理解
   3.前処理
   4.モデル構築
   5 .データの予測
   6.結果

1.House Pricesの概要

アイオワ州エイムズの住宅のほぼすべての特徴を表す79種類のデータを用いて、各住宅の価格を予測するというコンペです。
79種類のデータには、建物データ、土地データ、機能データ、住宅周辺に関するデータなど、様々な情報が含まれています。
価格の予測となるので、数値を予想する回帰問題（regression）となるのがこのコンペの特徴です。

2. データの理解

まずは、与えられるデータについて下記のデータが与えられます。
・train.csv :学習データ
・test.csv：テストデータ
・data_description.txt：79種類のデータの説明
sample_submission.csv :提出ファイルのサンプル
機械学習の中で、使うデータはtrain.csv, test.csvです。

train.csvにはSalePrice（住宅価格）が含まれますが、test.csvには含まれません。
train.csvのデータを使ってモデルを作成し、
その作成したモデルでtest.csvの住宅価格を予測します。

3.前処理

一部の数字が入っている変数を文字列に変換

結果

num2str_list = ['MSSubClass','YrSold','MoSold']
for column in num2str_list:
all_df[column] = all_df[column].astype(str)

LotFrontageの欠損値補完方法の検討について

train_df2 = train_df[['LotFrontage', 'LotArea', 'SalePrice', 'Neighborhood']].copy()
train_df2['LotFrontageNullFlag'] = np.where(train_df2['LotFrontage'].isnull(), 1, 0)
train_df2['LotFrontageNullFlag'].value_counts()

LotFrontageNullFlag
0 1201
1 259
Name: count, dtype: int64

まずは、欠損があるデータを0、欠損がないデータを1として、分けます。

train_df2.groupby('LotFrontageNullFlag')['SalePrice'].describe()

次に、住宅価格に対して、欠損があるデータ、欠損がないデータでグループ化しています。

import seaborn as sns
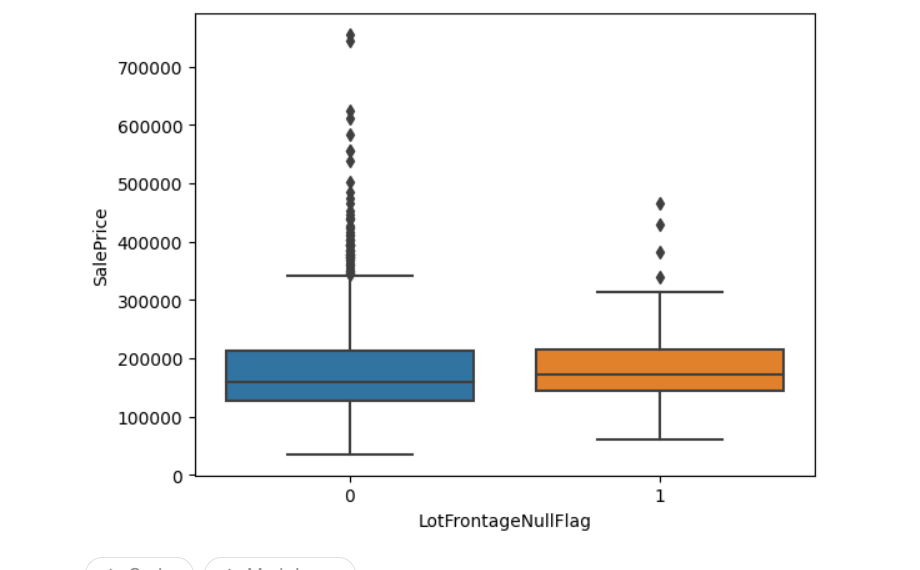
sns.boxplot(data=train_df2, y='SalePrice', x='LotFrontageNullFlag')

上記の結果を踏まえたうえで、可視化したところ、
欠損があるデータ、欠損がないデータで住宅価格の分布が変わらないので、
一番代表する値として、中央値で補完することにします。

欠損値処理

1.欠損値を含む行または列の削除
2.欠損値を代表値などで埋める

    変数の型ごとに欠損値の扱いが異なるため、変数ごとに処理
    for column in all_df.columns:
    # dtypeがobjectの場合、文字列の変数
    if all_df[column].dtype=='O':
        all_df[column] = all_df[column].fillna('None')
    # dtypeがint , floatの場合、数字の変数
    else:
        all_df[column] = all_df[column].fillna(train_df[column]. median())
        train_df[column] = train_df[column].fillna(train_df[column]. median())

そこで今回は、文字列の変数の欠損は「'None'」、
上記で説明しましたが、数字の変数の欠損は「中央値」で埋めるものとします。

特徴量の追加

予測精度が向上しそうな新しい変数を追加します。

    #特徴量エンジニアリングによりカラムを追加する関数
     def add_new_columns(df):
    #建物内の総面積 = 1階の面積 + 2階の面積 + 地下の面積
    df["TotalSF"] = df["1stFlrSF"] + df["2ndFlrSF"] 

    #一部屋あたりの平均面積 = 建物の総面積 / 部屋数
    df['AreaPerRoom'] = df['TotalSF']/df['TotRmsAbvGrd']

    # 築年数 + 最新リフォーム年 : この値が大きいほど値段が高くなりそう
    df['YearBuiltPlusRemod']=df['YearBuilt']+df['YearRemodAdd']

   
    # 合計の屋根付きの玄関の総面積 
    # Porch : 屋根付きの玄関 日本風にいうと縁側
    df['TotalPorchSF'] = (df['OpenPorchSF'] + df['3SsnPorch'] + df['EnclosedPorch'] + df['ScreenPorch'] + df['WoodDeckSF'])

    # プールの有無
    df['HasPool'] = df['PoolArea'].apply(lambda x: 1 if x > 0 else 0)

    # 2階の有無
    df['Has2ndFloor'] = df['2ndFlrSF'].apply(lambda x: 1 if x > 0 else 0)

    # ガレージの有無
    df['HasGarage'] = df['GrLivArea'].apply(lambda x: 1 if x > 0 else 0)

    

    # 暖炉の有無
    df['HasFireplace'] = df['Fireplaces'].apply(lambda x: 1 if x > 0 else 0)

    # カラムを追加
    add_new_columns(all_df)

カラムが追加されている確認します。

    print(all_df)

結果を表示するのは結構大変なので、省略します。

目的変数の変換

参考記事では正規分布に従うことを確認していましたが、
正規分布する必要性はないため、量的な説明変数の相関係数を求めて、
変換しない場合と対数変換した場合を比較するプログラムを実行しました。

まずはquantitativeの配列の要素数がいくらなのかを見ていきましょう。

print(len(quantitative))

36
次に、上記で説明した変換しない場合と対数変換した場合

quantitative = [f for f in train_df.columns if train_df.dtypes[f] != 'object']
quantitative.remove('SalePrice')

from scipy.stats import pearsonr
col_ls = []
pearson1_ls = []
pearson2_ls = []
for _i, _qc in enumerate(quantitative):
  col_ls.append(_qc)
  pearson1_ls.append(pearsonr(train_df[_qc], train_df['SalePrice'])[0])
  pearson2_ls.append(pearsonr(train_df[_qc], np.log(train_df['SalePrice']))[0])

quantitative_corr_df = pd.DataFrame({'column_name':col_ls, 'PearsonR_raw':pearson1_ls, 'PearsonR_log':pearson2_ls})
quantitative_corr_df.head()
# 対数変換したほうが線形性がより満たされる説明変数の個数
quantitative_corr_df[np.abs(quantitative_corr_df.PearsonR_raw) <= np.abs(quantitative_corr_df.PearsonR_log)].shape[0]

23

23という数字が過半数を占めていることが確認できました。

文字列を変数化

文字列が入っている変数はそのままでは、正規化したり機械学習にかけられないので、One-Hot-Encodingによりカテゴリ変数化します。

     pd.get_dummiesを使うとカテゴリ変数化できる
     all_df = pd.get_dummies(all_df)
     all_df.head()

これにより、文字列が入ってた列がカテゴリ変数化になりました。

外れ値

学習データから特異な物件のデータは削除しますが、予測データの物件は削除できないので、学習データに対してのみ実施します。

    学習データと予測データに分割して元のデータフレームに戻す
train_df = pd.merge(all_df.iloc[train_df.index[0]:train_df.index[-1]],train_df['SalePrice'],left_inex=True,right_index=True)test_df = all_df.iloc[train_df.index[-1]:]

一行で表示しておりますが、実装する際には２行にした方が良いです。

train_df = train_df[(train_df['LotArea']<20000) & (train_df['SalePrice']<400000)&(train_df['YearBuilt']>1920)]

上記で、記載したコードは、以下の条件にあてはまるものを外れ値の定義し、該当するデータを削除します。
1.物件の価格が400,000ドル以上
2.敷地面積が20,000平方メートル以上
3.建築年が1920年より前
以上の３つをなぜ外れ値に設定したのかを可視化します。
まずは、'LotArea'（敷地面積）から、可視化で見てみましょう。

import matplotlib.pyplot as plt

マットプロットリブをインポートしましょう。

plt.boxplot(train_df['LotArea'])

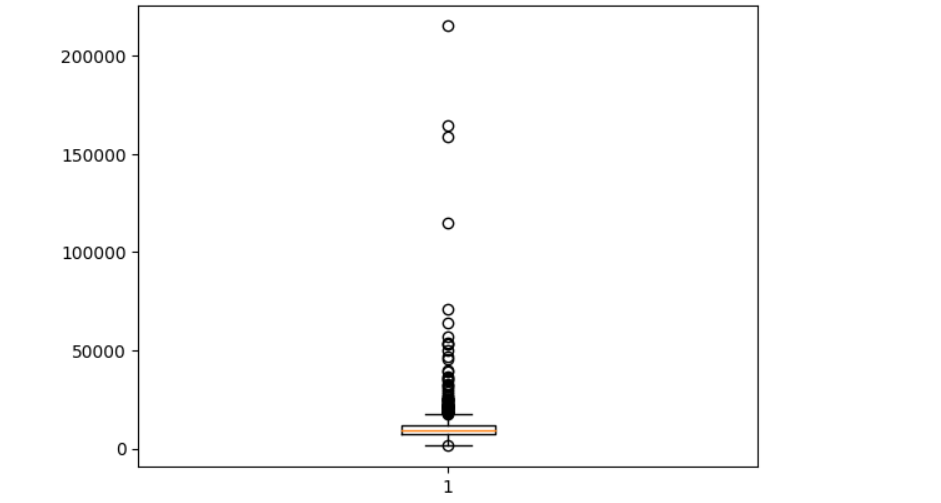
箱ひげで可視化しました。可視化すると、20,000平方メートルを境に外れ値になってきています。
続いて、'SalePrice'（住宅価格）も箱ひげで可視化してみましょう。

plt.boxplot(train_df['SalePrice'])

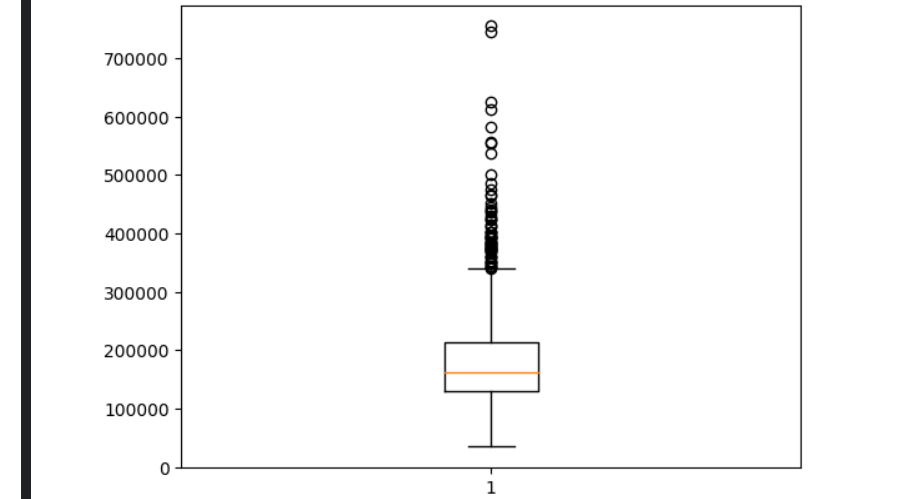
可視化してみたら、やはり、400,000ドル以上を境に外れ値が多くなってきてます。

最後に、'YearBuilt'の可視化ですが、箱ひげ図ではなく、ここで、販売価格とどのような影響があるのか散布図で可視化してみました。
まずは、

いよいよ、散布図を可視化します。

plt.scatter(train_df['YearBuilt'],train_df['SalePrice'] )
plt.xlabel('YearBuilt')
plt.ylabel('SalePrice')
plt.show()

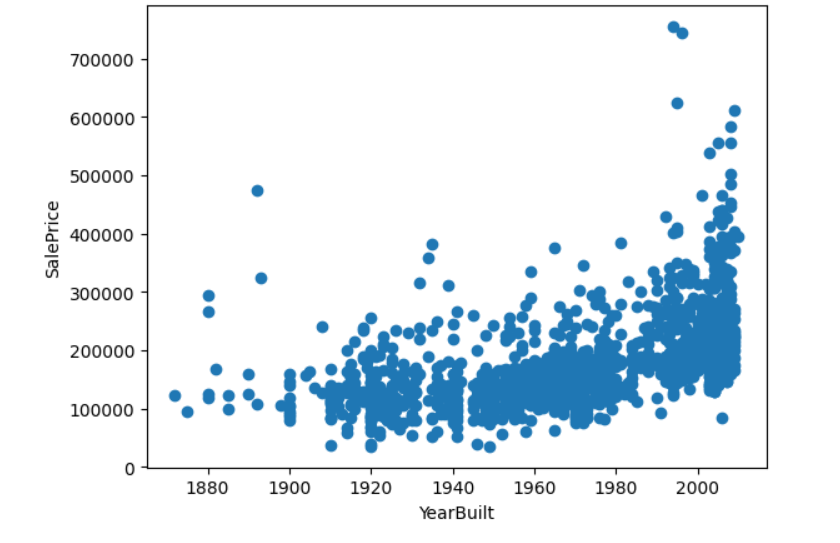
やはり、散布図も1920年前よりは、外れ値の値がちらほら見えてます。
なので、1920年前の建物は外れ値として処理します。

住宅価格を対数変換と変換しない場合

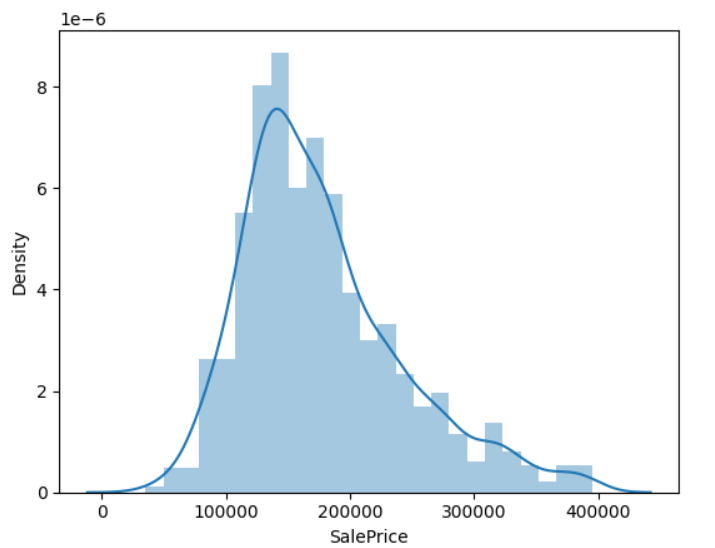
    sns.distplot(train_df['SalePrice'])
    print(f"歪度: {round(train_df['SalePrice'].skew(),4)}" )
    print(f"尖度: {round(train_df['SalePrice'].kurt(),4)}" )

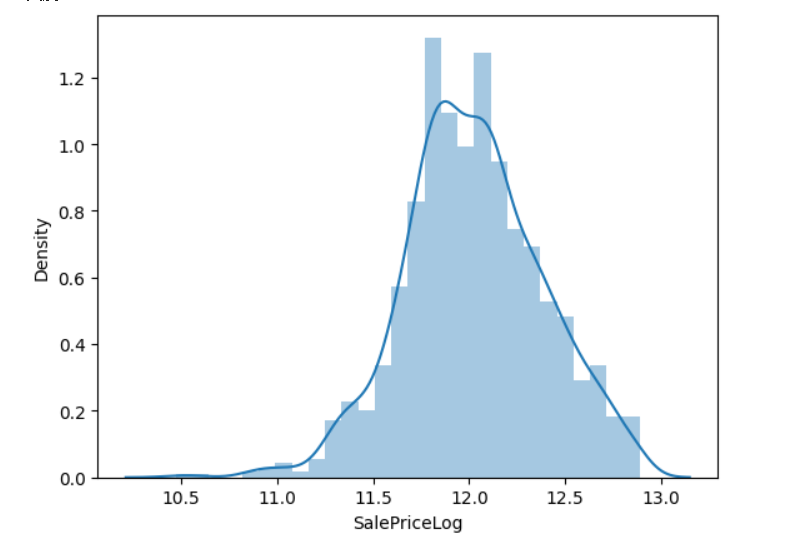
      train_df['SalePriceLog'] = np.log(train_df['SalePrice'])
      sns.distplot(train_df['SalePriceLog'])
      print(f"歪度: {round(train_df['SalePriceLog'].skew(),4)}" )
      print(f"尖度: {round(train_df['SalePriceLog'].kurt(),4)}" )

上記のように、正規分布を可視化したグラフを作成しました.

回帰モデルの作成

目的変数

y = df_train['SalePrice']

説明変数

X = train_df[['OverallQual', 'YearBuilt', 'TotalBsmtSF', 'GrLivArea','LotFrontage','LotArea', 'YearRemodAdd', 'BsmtFinSF1', 'BsmtUnfSF','1stFlrSF', '2ndFlrSF','TotalPorchSF', 'WoodDeckSF', 'OpenPorchSF', 'GarageArea' ]]

学習用、検証データに分割

(X_train, X_test, y_train, y_test) = train_test_split(X, y, test_size = 0.2, random_state = 5)

Ridge回帰の対比として 回帰モデルの作成

model = linear_model.LinearRegression()
model.fit(X_train, y_train)

学習データの決定係数を確認する

model.score(X_train, y_train)

テストデータの決定係数も確認する

model.score(X_test, y_test)

学習済みの予測モデルをもとに予測する計算式

print(model.coef_)
print(model.intercept_)

上記のコードで
model.coef_で各要素の重みを、model.intercept_で切片を表しています。

予測値の算出

y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)

予測結果の確認

print('R2(Train) : % 0.3f' % r2_score(y_train,  y_train_pred))
print('R2(Test) : % 0.3f' % r2_score(y_test, y_test_pred))

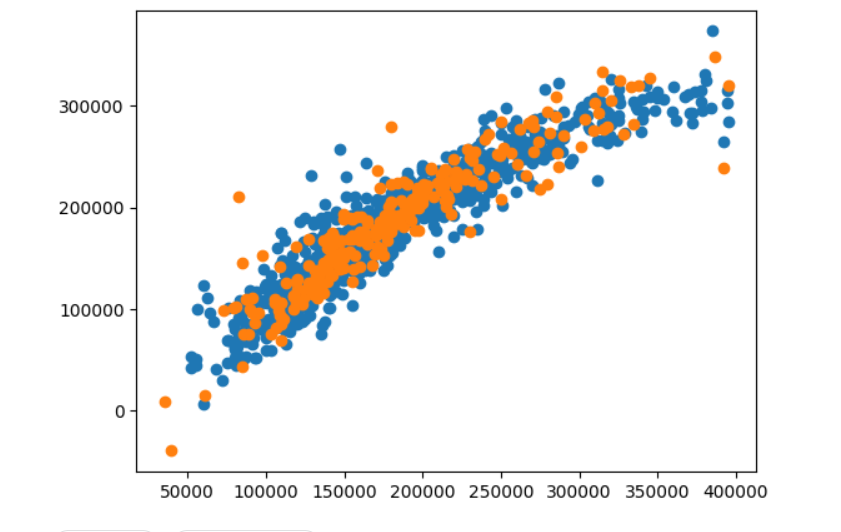
グラフの可視化

plt.scatter(y_train, y_train_pred)
plt.scatter(y_test, y_test_pred)
plt.show()

学習データ、予測データフレームに分割する

学習データは説明変数、目的変数、予測データは目的変数に分けてデータフレームにする。

      train_X = train_df.drop(columns = ['SalePrice','SalePriceLog'])
      train_y = train_df['SalePriceLog']
      test_X = test_df

Ridge回帰モデル作成

機械学習アルゴリズムとしてリッジ回帰（Ridge regression）を選んだ理由は
正則化パラメータを調整することで、モデルの複雑さを抑え、
過学習のリスクを低減させるのが特徴的なので、よりよい精度が出せると思いました。

ホールドアウト検証、ハイパーパラメータを用いる

def ridge_tuning(X_train,y_train):
    # alphaパラメータのリスト
    param_list = [0.001, 0.01, 0.1, 1.0, 10.0,100.0,1000.0] 

    for cnt,alpha in enumerate(param_list):
        # パラメータを設定したリッジ回帰モデル
        ridge = Ridge(alpha=alpha) 
        # パイプライン生成
        pipeline = make_pipeline(StandardScaler(), ridge)

        # 学習データ内でホールドアウト検証のために分割 テストデータの割合は0.3 seed値を0に固定
        X_train, X_test, y_train, y_test = train_test_split(X_train, y_train, test_size=0.3, random_state=0)

        # 学習
        pipeline.fit(X_train,y_train)

        # RMSE(平均誤差)を計算
        train_rmse = np.sqrt(mean_squared_error(y_train, pipeline.predict(X_train)))
        test_rmse = np.sqrt(mean_squared_error(y_test, pipeline.predict(X_test)))
        # ベストパラメータを更新
        if cnt == 0:
            best_score = test_rmse
            best_param = alpha
        elif best_score > test_rmse:
            best_score = test_rmse
            best_param = alpha

    # ベストパラメータのalphaと、そのときのMSEを出力
    print('alpha : ' + str(best_param))
    print('test score is : ' +str(round(best_score,4)))

    # ベストパラメータを返却
    return best_param

# best_alphaにベストパラメータのalphaが渡される。
best_alpha = ridge_tuning(train_X,train_y)

結果

alpha : 0.001
test score is : 0.1141

この結果がベストなパラメータになるので、それを用いて、モデル作成行います。

    # リッジ回帰モデルにベストパラメータを設定
ridge = Ridge(alpha = best_alpha)
     # パイプラインの作成
pipeline = make_pipeline(StandardScaler(), ridge)
     # 学習
pipeline.fit(train_X,train_y)

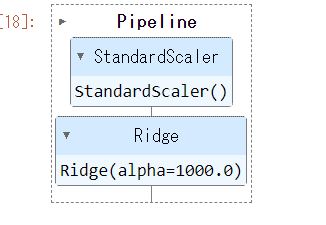
変換器：StandardScaler（標準化）
予測器（推定器）：Ridge（リッジ回帰）モデルのベストなパラメータ
変換器、予測器（推定器）をそれぞれ定義して、繋げたのが下の図になります。

学習データでパイプラインを構築（学習）します。

リッジ回帰式の係数を表示します。

coefficients = ridge.coef_
print("係数", coefficients )

結果

係数 [-5.64785353e-04  2.23235526e-02  4.30555969e-02  3.40972524e-02
  4.11454298e-02 -8.11312749e-04  5.20660135e-03  2.08813638e-02
  4.98324030e-03 -9.78647393e-04  2.28720848e-02  1.17047543e-02
  1.44142292e-02  1.31893062e-04  2.21680589e-02  1.70516699e-02
  3.82855930e-03  1.48744794e-02  8.86311815e-03 -8.36732169e-04
 -1.03914643e-03  4.92027667e-02  4.91627929e-03 -3.08076025e-05
  1.86742790e-02  1.36937371e-02  4.62390950e-03  4.83654892e-03
 -2.16613640e-03  3.23705260e-03  7.86110406e-03  1.99882877e-02
  1.52034818e-02  2.21625644e-02  4.18344213e-02  2.43695169e-02
  8.48461599e-03 -3.88087000e-03 -2.12064980e-02  0.00000000e+00
  2.07387259e-03  3.97816996e-03  0.00000000e+00 -1.44266596e-02
 -5.05162598e-03 -1.96676429e-02  9.59446292e-03 -3.88419642e-03
  2.23611146e-03  5.95166988e-04 -3.85961962e-03  6.90869509e-03
  1.26406968e-02  1.29400310e-02 -1.32094934e-02  1.33705128e-03
 -5.88674513e-03 -3.09538248e-02  1.44312002e-02  0.00000000e+00
 -2.04097128e-03  4.12779935e-03 -9.34892075e-03  3.96642146e-03
 -3.96642147e-03  1.17198520e-03 -9.50179678e-04  2.58831859e-04
 -2.57415372e-03  1.37465308e-03  1.86382352e-04  2.10787605e-03
  5.10305081e-04  2.02816449e-03 -4.27518634e-03  2.92067236e-04
  3.59445981e-03 -3.59445981e-03  0.00000000e+00  4.49258623e-03
  5.93686053e-03 -5.98498045e-03 -1.83501837e-03 -4.34699167e-03
  3.14226358e-03 -1.93346200e-03 -5.19898702e-03  3.36399694e-03
  2.28737209e-03  2.32492314e-03  1.84505499e-03  1.80162004e-03
 -2.26084552e-03  2.59052473e-02 -1.35539116e-02 -1.60739499e-03
 -1.12667975e-03 -1.05047983e-02 -7.12131709e-03 -8.84855913e-03
  2.76822006e-03 -6.47270583e-03  7.42764338e-03  1.35062322e-02
 -5.98459805e-03 -2.88214437e-03 -2.87235581e-03  9.46730605e-04
  4.14130946e-03  1.86115967e-02  1.21059591e-03  2.55303769e-03
 -1.12897516e-02 -6.41664159e-04  8.22956130e-03 -1.93934888e-03
  1.84384397e-03 -1.07436776e-02  1.11426676e-03 -1.64895655e-03
  1.64047862e-03  7.48803102e-04 -6.04533884e-03  3.13244464e-03
  0.00000000e+00 -1.91697479e-03  6.57944939e-04 -1.46180154e-03
  1.19023708e-03  8.02289057e-03  1.10131661e-02 -5.88674512e-03
 -5.84668555e-03 -6.79713604e-03  1.34649062e-02  7.80712250e-04
 -8.07133184e-03 -9.00618588e-03 -1.05848009e-02 -4.12024671e-03
 -1.75068203e-03  1.33744584e-02  2.83109842e-03 -5.60505598e-04
 -2.42261544e-04 -2.79394659e-05  4.37361814e-04  6.57944935e-04
  0.00000000e+00  9.93649902e-04  0.00000000e+00  0.00000000e+00
 -1.66454583e-03  3.47729284e-04 -2.85524154e-04 -1.68482269e-03
  6.54830192e-03 -1.11270836e-03 -1.37639658e-02  1.36277538e-02
  0.00000000e+00 -2.08123426e-02 -2.74028413e-03 -3.73994605e-04
  1.23066101e-02  0.00000000e+00 -5.63188753e-04 -1.49746367e-03
 -3.46578898e-03  7.13816970e-04 -6.25773260e-03  2.75305598e-03
 -6.70467724e-03  1.57332707e-03  5.91464604e-03 -2.65802878e-03
  0.00000000e+00  2.14479930e-02 -4.15442909e-03 -6.48423412e-04
 -5.51625942e-03  0.00000000e+00 -2.74834825e-03 -6.35206426e-03
  3.71137280e-04  8.68672082e-03 -1.51977675e-03  5.89303397e-03
 -1.29129956e-03 -6.58824328e-03 -6.46885444e-05 -2.99855584e-03
  7.65883253e-03  1.87750147e-03 -4.47779084e-03  5.16008830e-04
 -3.08310449e-04  1.46105208e-03  4.29919412e-04 -4.09319812e-03
  1.16396538e-03  3.37221099e-03  1.93990071e-03 -4.27893403e-03
  4.34677822e-03 -3.18192472e-04 -2.98589274e-03 -7.22370333e-03
  4.84944730e-03 -5.43599327e-03 -2.37373774e-03 -2.05028439e-04
  1.10713382e-03 -7.64221930e-03  1.65259833e-03 -2.05028433e-04
  5.82033913e-03  2.04900311e-03 -2.30441771e-04  1.25726686e-02
 -8.80421522e-04 -3.05820716e-03 -9.64926470e-03  7.66167743e-04
 -3.13083960e-03  6.61198899e-03 -4.73129579e-03 -2.05028441e-04
 -2.25379000e-03 -1.40873000e-03  2.86431516e-03 -5.85539371e-03
  2.03991598e-03  4.65325534e-04 -1.68452555e-04 -8.16968513e-04
  1.34275086e-03 -4.21363117e-03 -2.87430559e-04  7.40717933e-03
 -6.15684305e-03  0.00000000e+00  4.97534861e-04  6.29918767e-03
 -3.67285302e-03 -9.38348643e-04 -1.24146105e-03 -4.69142485e-03
 -3.42258080e-03  3.42258080e-03  2.22393612e-03  6.49724022e-04
 -2.36576938e-03  0.00000000e+00  1.92573994e-03 -2.11120461e-03
  1.56019502e-02 -5.23669558e-03 -2.77334240e-03  0.00000000e+00
 -3.05730514e-03 -3.14331807e-03 -1.19129869e-02  2.27673425e-04
  5.01477042e-04 -1.03503687e-02  0.00000000e+00 -7.73344085e-03
  8.04776359e-03 -2.32238093e-03 -1.90600164e-03  3.15796693e-03
 -2.07387259e-03  1.75900413e-04  4.59658911e-04 -2.40637397e-03
  5.63359425e-04  5.00078050e-04 -1.76949209e-03 -2.70703038e-03
  1.34171772e-03 -8.25256226e-04  1.35397378e-03 -8.25256226e-04
  2.12521348e-03 -2.85928420e-03  2.10319790e-03 -7.67602876e-03
  5.13606687e-03 -8.25256227e-04 -2.08971796e-03  3.04937785e-03
  2.10319789e-03  7.74268094e-04 -3.42030795e-03 -8.25256227e-04
  4.12416623e-04  9.11843075e-04 -1.57731539e-03 -2.39480284e-03
  2.68426037e-03  0.00000000e+00 -5.05563813e-03 -4.28420755e-04
  3.88087000e-03 -9.86082651e-04 -3.72257964e-03  2.42937576e-03
 -1.66418265e-03  7.61143531e-04 -1.43067772e-02  3.16312995e-03
  6.75731900e-06  8.36003548e-04 -6.40416534e-03 -4.35477060e-03
 -1.82247838e-03  3.52106404e-05  3.56184455e-04 -2.07423870e-03
 -2.77027495e-03  6.57893500e-04  2.50025481e-03  2.43658425e-03
 -1.41089914e-04  2.73180371e-04  1.30257735e-03  2.60174335e-03
  5.30078455e-04  5.98209855e-04 -3.49681421e-03 -1.73947041e-04
  3.20538559e-03  5.76094856e-03  4.41964710e-03  6.97673260e-03
  1.94092616e-03  3.15931447e-03 -1.36865009e-02  0.00000000e+00
  3.11823567e-03  5.53420817e-03 -1.69316870e-02  1.91323045e-03
 -3.62806816e-04 -7.96535349e-03 -3.42554515e-03  2.28224266e-02]

どの説明変数が主に予測へ寄与しているかを以下のコードにしました。

coefficients  = ridge.coef_
abs_coefficients = np.abs(coefficients)
max_index = np.argmax(abs_coefficients)
max_coefficient = abs_coefficients[max_index]
max_feature = train_X.columns [max_index]

print(f"最も影響力のある説明変数: {max_feature}, 係数: {max_coefficient}")

最も影響力のある説明変数: TotRmsAbvGrd, 係数: 0.04920276670906913という結果になりました。

住宅価格を予測

先ほどの学習データで構築（学習）したパイプラインを使い、テストデータで予測し精度検証していきます。

    pred = pipeline.predict(test_X)

予測結果を可視化

    sns.distplot(pred)
    print(f"歪度: {round(pd.Series(pred).skew(),4)}" )
    print(f"尖度: {round(pd.Series(pred).kurt(),4)}" )

次に、対数変換した値を目的変数としているため、予測された値も対数変換になっています。
そこで、予測した値を指数変換してあげる必要があります。
以下のコードで変換していきます。

       # 指数変換
        pred_exp = np.exp(pred)
         # 指数変換した予測結果をプロット
         sns.distplot(pred_exp)
        # 歪度と尖度
   print(f"歪度: {round(pd.Series(pred_exp).skew(),4)}" )
   print(f"尖度: {round(pd.Series(pred_exp).kurt(),4)}" )

変換した後はいよいよ提出CSVを作成していきたいと思います。

提出用CSV作成

データの理解の説明のなかに、sample_submission.csvがありましたが、
こちらのCSVを読み込んで、提出用CSVを作成する流れになります。
以下のコードで行います。

    submission_df = pd.read_csv('/kaggle/input/house-prices-advanced-regression-techniques/sample_submission.csv')

さらにsample_submission.csvの形式を確認するため、全部を確認するのは難しいので、
最初の5行に指定して、確認します。

    submission_df.head()

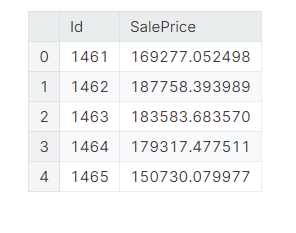
1列目にId、2列目にSalePrice(予測した住宅価格）が表示されています。

CSVを出す前に、エラーなどが入っていないか（例えば外れ値の削除などで行が誤って削除されている）など、間違った処理をしているとエラーがおきないかを確認するコードがあります。

    submission_df['SalePrice'] = pred_exp

上記のコードを実装したところ、エラーが起きませんでした。
最後に、kaggleの提出用CSVを出力していきます。

    submission_df.to_csv('submission.csv',index=False)

※index=Falseにするかというと、各行の名前を書きださないという意味です。

上記で結果は記載いたしましたが、まだまだ回帰分析の基礎の流れを行いました。
今回kaggleのコンペに挑戦できたことは、自分の成長にもつながりましたし、
もっとどうしたら精度が上がるのかを考させられる部分がいっぱいありました。
結果として、機械学習が楽しみながら、学ぶのが一番の近道だと思っています。

最後までご覧になっていただき、ありがとうございます。