LoginSignup
8
9
@yusuke_s_yusuke(Yusuke Sakai)in立教大学

Richardson-Lucy deconvolutionの特徴をシミュレーションで理解しよう（前編：シミュレーションの実装）

Last updated at Posted at 2022-02-19

はじめに

Richardson-Lucy deconvolution（以下、RL法）は、画像等を鮮明にする手法である。一般的な撮像観測では、観測装置の回折等により光源が拡がって撮像される。この拡がり具合は、点拡がり関数(Point Spread Function, 以下、PSF)で表される。RL法は既知のPSFと撮像画像から、真の画像を推定する手法である。
図1.png

本シリーズの目標

実際の撮像観測では真の画像は知り得ないので、RL法により推定された真の画像は、本当に真の画像に近づいているか分からない。そこで、本シリーズでは、真の画像とPSFが完全にわかっていて、かつノイズが乗らない理想的な状況でのシミュレーションにより、RL法の特徴を理解する。
本シリーズは3部構成（前編：シミュレーションの実装、中編：結果の解析、後編：補足）で、気長に記事にしていく予定である。（お楽しみに！）

RL法とは

RL法は、既知のPSFと撮像画像を用いて真の画像を推定する手法である。真の画像の分布、既知のPSF、撮像画像の関係をベイズの定理を用いて関係づける。そして、ベイズ推定を繰り返し計算することにより真の画像を推定する。理論式は

 W_{i,r+1} = W_{i,r}\sum_k \frac{P_{i,k}H_k}{\sum_j P_{j,k}W_{j,r}}\
\quad r = 0,\ 1,\  2,\  \dots

と表される。$j,k$はピクセル座標とする。$W$は真の画像、$H$は撮像画像、$r$は反復回数とする。$P_{j,k}$はPSFで、$W_j$が$H_k$で観測される確率を$P(H_k|W_j)=P_{j,k}$とする。式の導出は、私の記事で恐縮ですが、Richardson-Lucy deconvolutionの理論式を導出しようを参照されたい。

シミュレーションの実装

Google Colabで作成した本記事のコードは、こちらにあります。

各種インポート

各種インポート
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import matplotlib.cm as cm
from scipy.stats import norm  # おまけの項で使います
from scipy.stats import multivariate_normal
from scipy.signal import convolve
from skimage import restoration

実行時の各種バージョン

Name Version
numpy 1.21.5
matplotlib 3.2.2
scipy 1.4.1
scikit-image 0.18.3

※scikit-imageのrestoration.richardson_lucyは、Version 0.19.1で一部変更されている。（変更箇所概要：Add small regularization to avoid zero-division in richardson_lucy (gh-5976))

PSF作成用の関数

PSF作成用の関数
def get_psf(px, sigma):
    half_px = px // 2
    x, y = np.mgrid[-half_px:half_px+1:, -half_px:half_px+1:]
    pos = np.dstack((x, y))
    mean = np.array([0, 0])  # 分布の平均
    cov = np.array([[sigma**2, 0], [0, sigma**2]])  # 分布の分散共分散行列
    rv = multivariate_normal(mean, cov)
    psf = rv.pdf(pos)
    return psf

シミュレーションに使用するPSFは何でも良いが、今回は多変量正規分布に従うPSFで実装する。多変量正規分布にはSciPyのmultivariate_normalを使用する。
多変量正規分布の性質については、多変量正規分布の性質を図で解説するや多変量正規分布をPythonでplotして理解するを参照されたい。

RL法のシミュレーション

RL法のシミュレーション
"""シミュレーション"""
# 真の画像
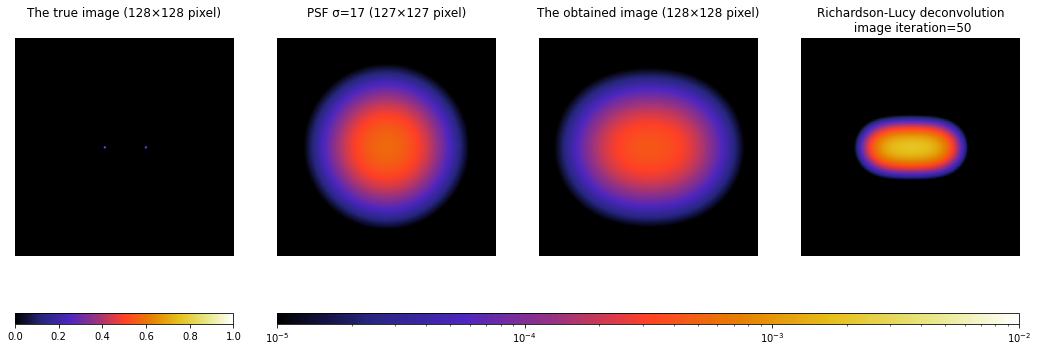
true_px = 128
true_img = np.zeros([true_px, true_px])
true_img[64, 52] = 0.5
true_img[64, 76] = 0.5

# PSF
psf_px = 127
psf_sigma = 17
psf = get_psf(psf_px, psf_sigma)

# 真の画像をPSFで畳み込む（撮像画像）
obtained_img = convolve(true_img, psf, "same")

# RL法
iterations = 50
rl_img = restoration.richardson_lucy(obtained_img, psf, iterations)

"""シミュレーションの結果を図に表示"""
fig, (ax1, ax2, ax3, ax4) = plt.subplots(figsize=(18, 7), ncols=4)
cbar_min = 1e-5
cbar_max = 1e-2

# 真の画像
ax1.set_title("The true image ({0}×{0} pixel)\n".format(true_px))
cbar1 = ax1.imshow(true_img, cmap=cm.CMRmap, vmin=0, vmax=1)
ax1.axis("off")
fig.colorbar(cbar1, ax=ax1, orientation="horizontal")

# PSF
ax2.set_title("PSF σ={0} ({1}×{1} pixel)\n".format(psf_sigma, psf_px))
psf_display = np.where(psf < cbar_min, cbar_min, psf)
ax2.imshow(psf_display, cmap=cm.CMRmap,
           norm=colors.LogNorm(vmin=cbar_min, vmax=cbar_max))
ax2.axis("off")

# 撮像画像
ax3.set_title("The obtained image ({0}×{0} pixel)\n".format(true_px))
obtained_img_display = np.where(obtained_img < cbar_min, cbar_min, obtained_img)
ax3.imshow(obtained_img_display, cmap=cm.CMRmap,
           norm=colors.LogNorm(vmin=cbar_min, vmax=cbar_max))
ax3.axis("off")

# RL法による生成画像
ax4.set_title("Richardson-Lucy deconvolution\n image iterations={0}".format(iterations))
rl_img_display = np.where(rl_img < cbar_min, cbar_min, rl_img)
cbar2 = ax4.imshow(rl_img_display, cmap=cm.CMRmap,
                   norm=colors.LogNorm(vmin=cbar_min, vmax=cbar_max))
ax4.axis("off")
fig.colorbar(cbar2, ax=[ax2, ax3, ax4], orientation="horizontal", aspect=70)

plt.show()

  • 出力結果
    Unknown-118.png

  • コードの概念図
    図1.png

  • コードの説明

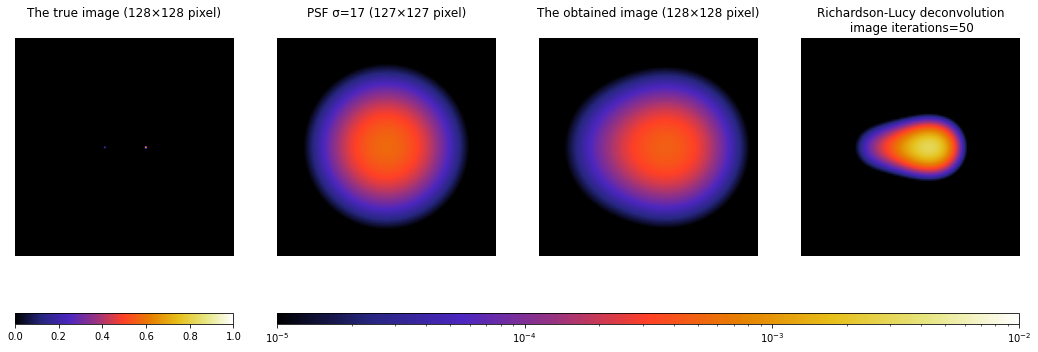
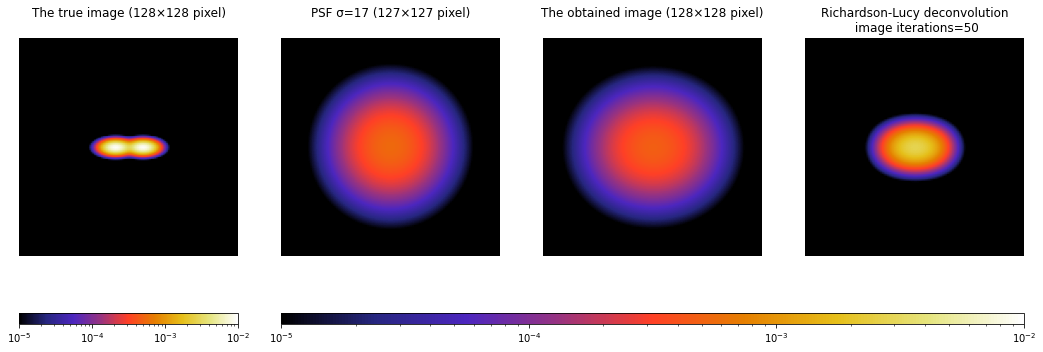
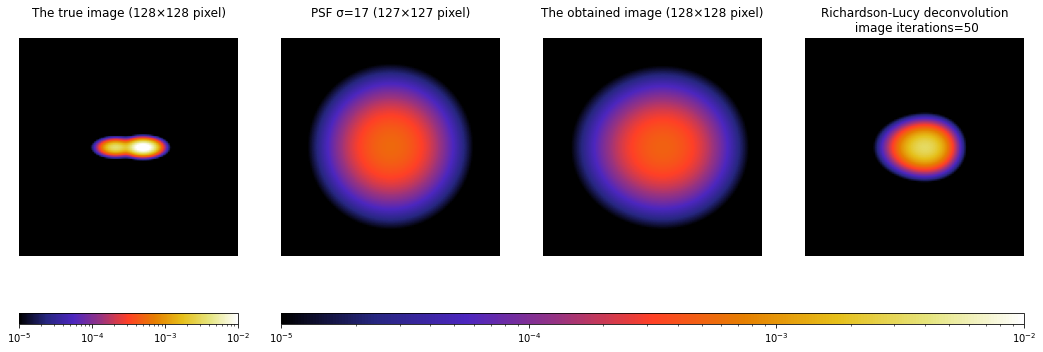
    1. 真の画像とPSFを用意する。上の例では、真の画像はピクセル座標[64, 52], [64, 76]に0.5の値を入れたものを用いる。PSFは多変量正規分布の分散共分散行列の標準偏差σを、psf_sigma=17として用いる。
      ※PSFのピクセルサイズpsf_pxは、奇数が望ましい。奇数だとPSFの中心のピクセル座標が一意に決まるので、真の画像をPSFで畳み込むときやRL法が上手くいく。（偶数のピクセルサイズでも畳み込み自体は実行できるが、意図せぬ（ある法則に従った）ピクセル座標を中心とした畳み込みが行われるので、注意したい。）
    2. 真の画像をPSFで畳み込み、撮像画像を作成する。
    3. 撮像画像と2と同じPSFで、RL法を行う。
      ※***_display = np.where(*** < cbar_min, cbar_min, ***)は、対数のカラーバーでは0や非常に小さい値は上手く表示できないため、カラーバーの最小値より小さい値をカラーバーの最小値に置換している。

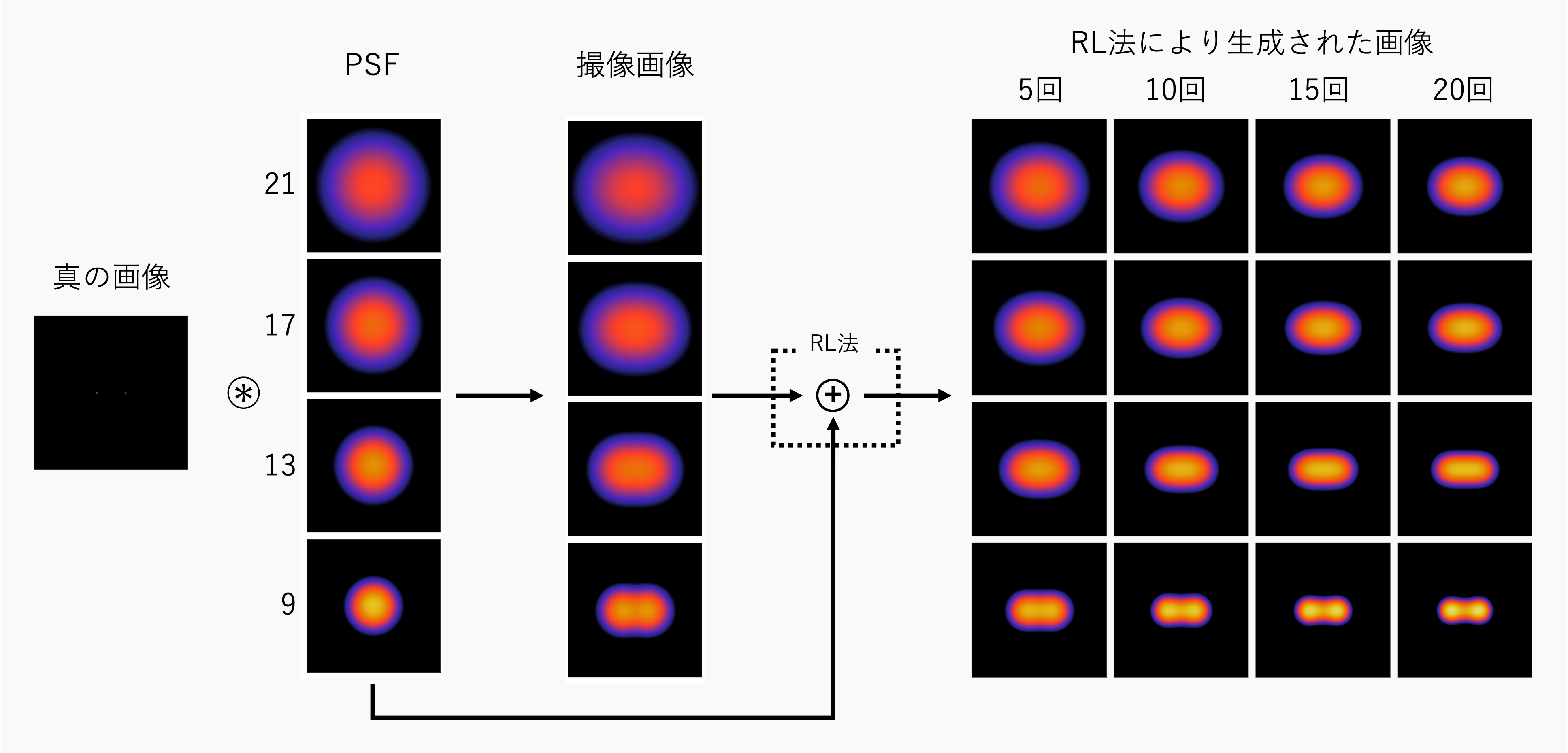
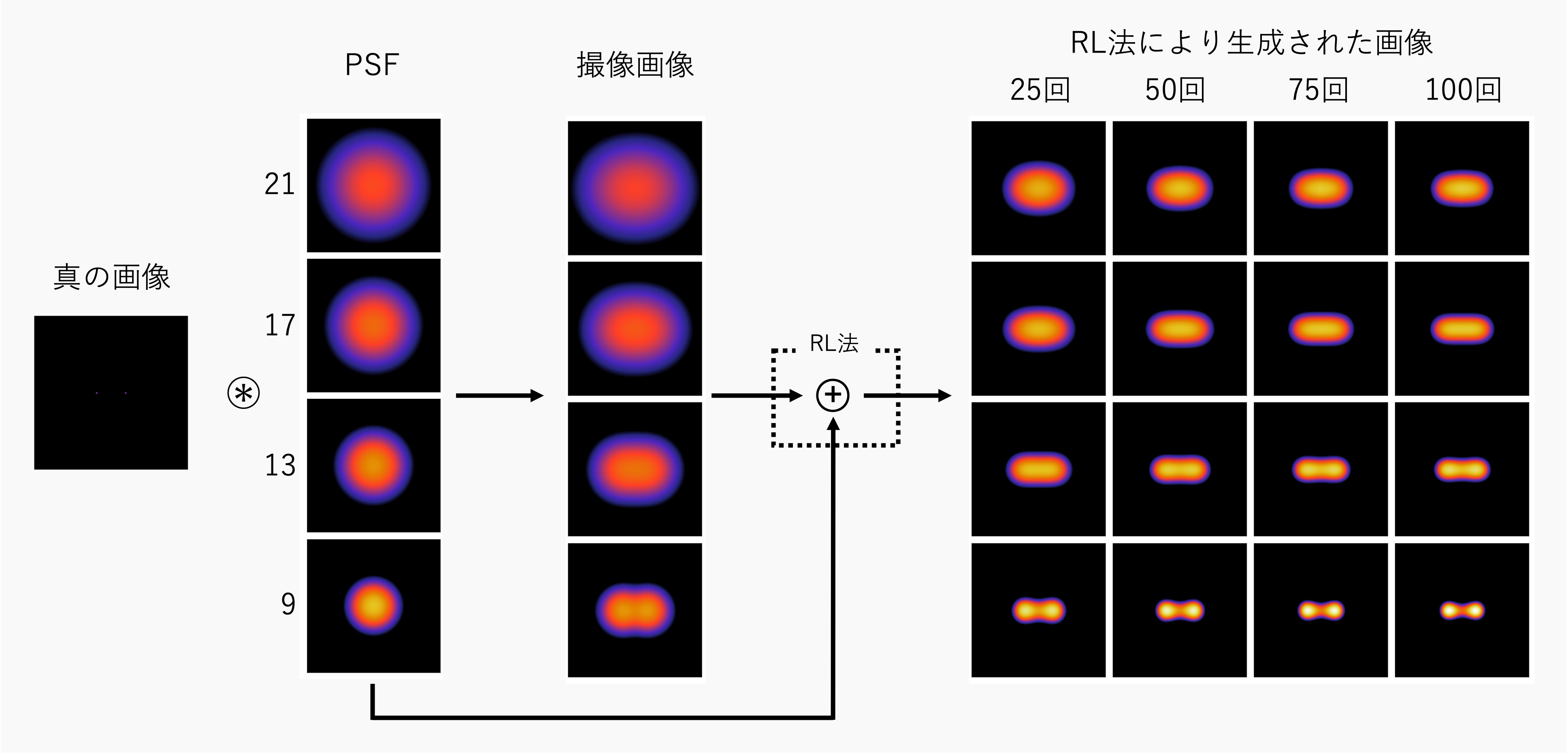
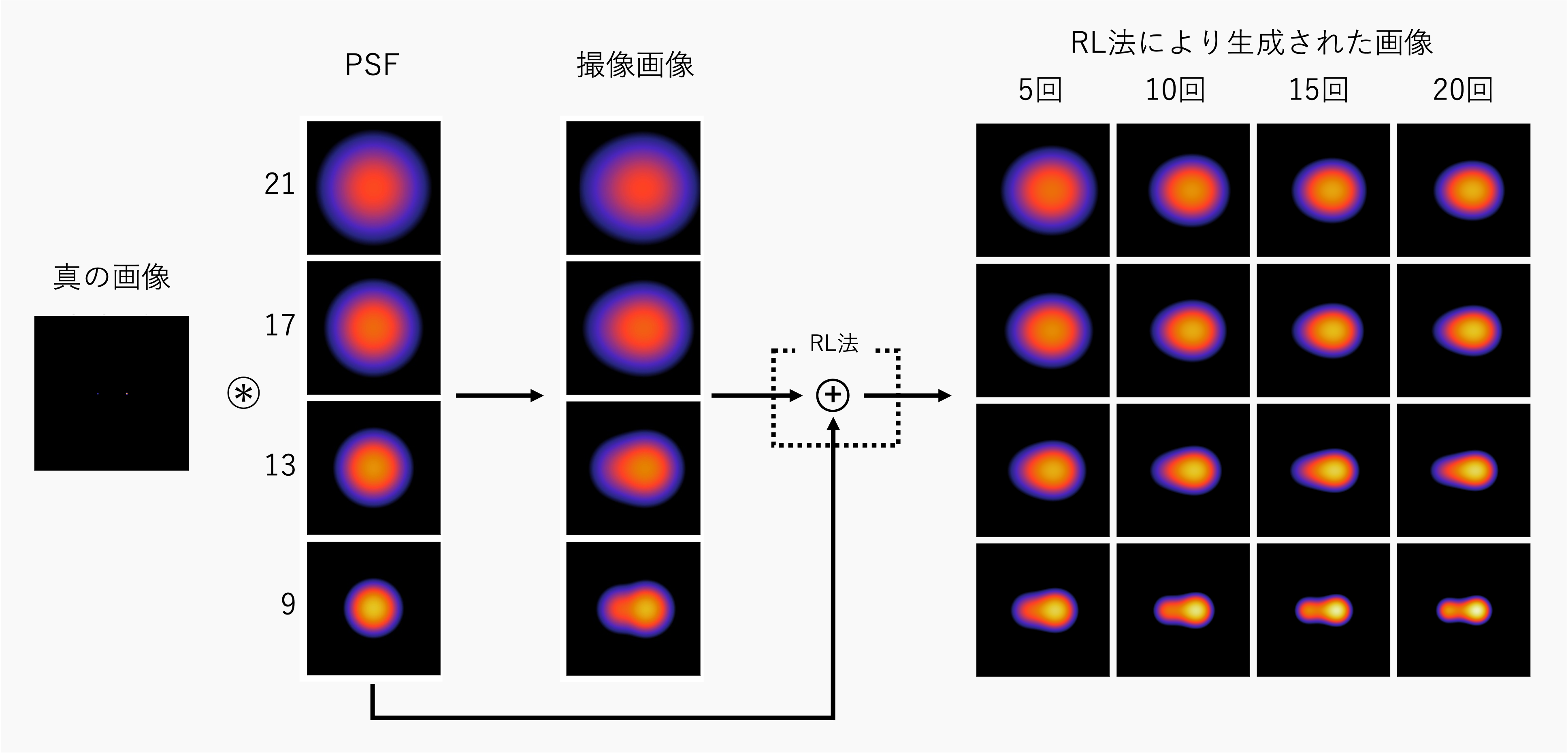
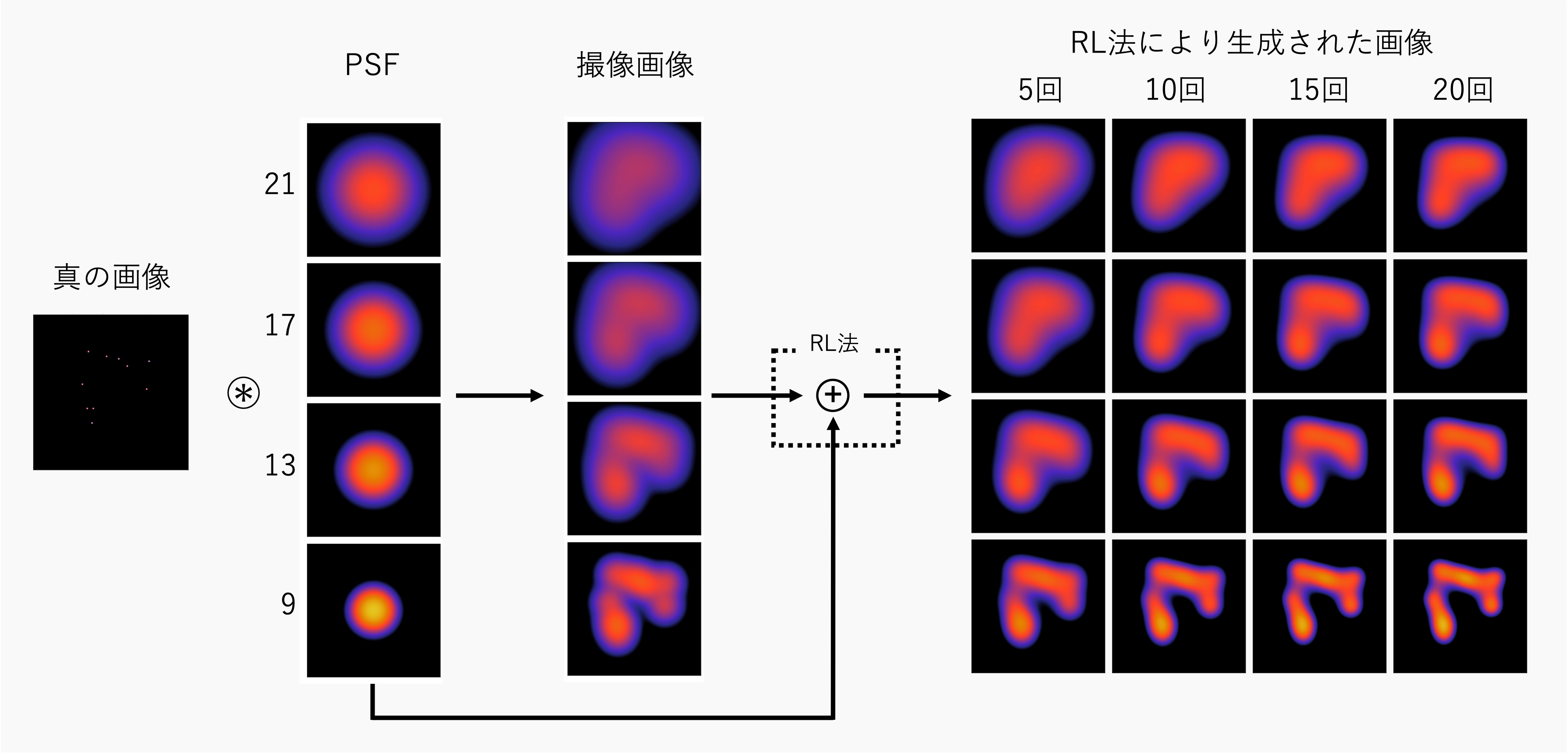
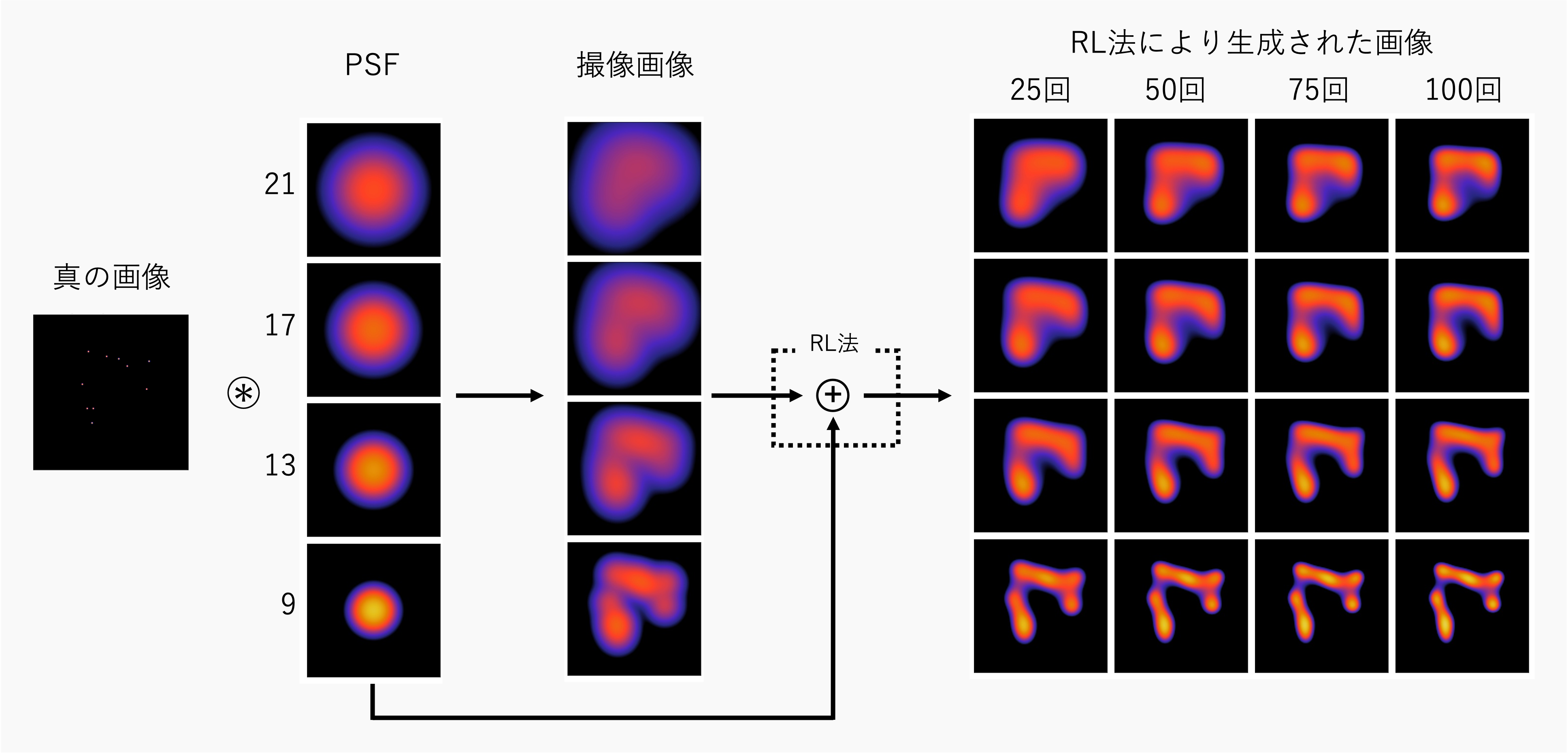
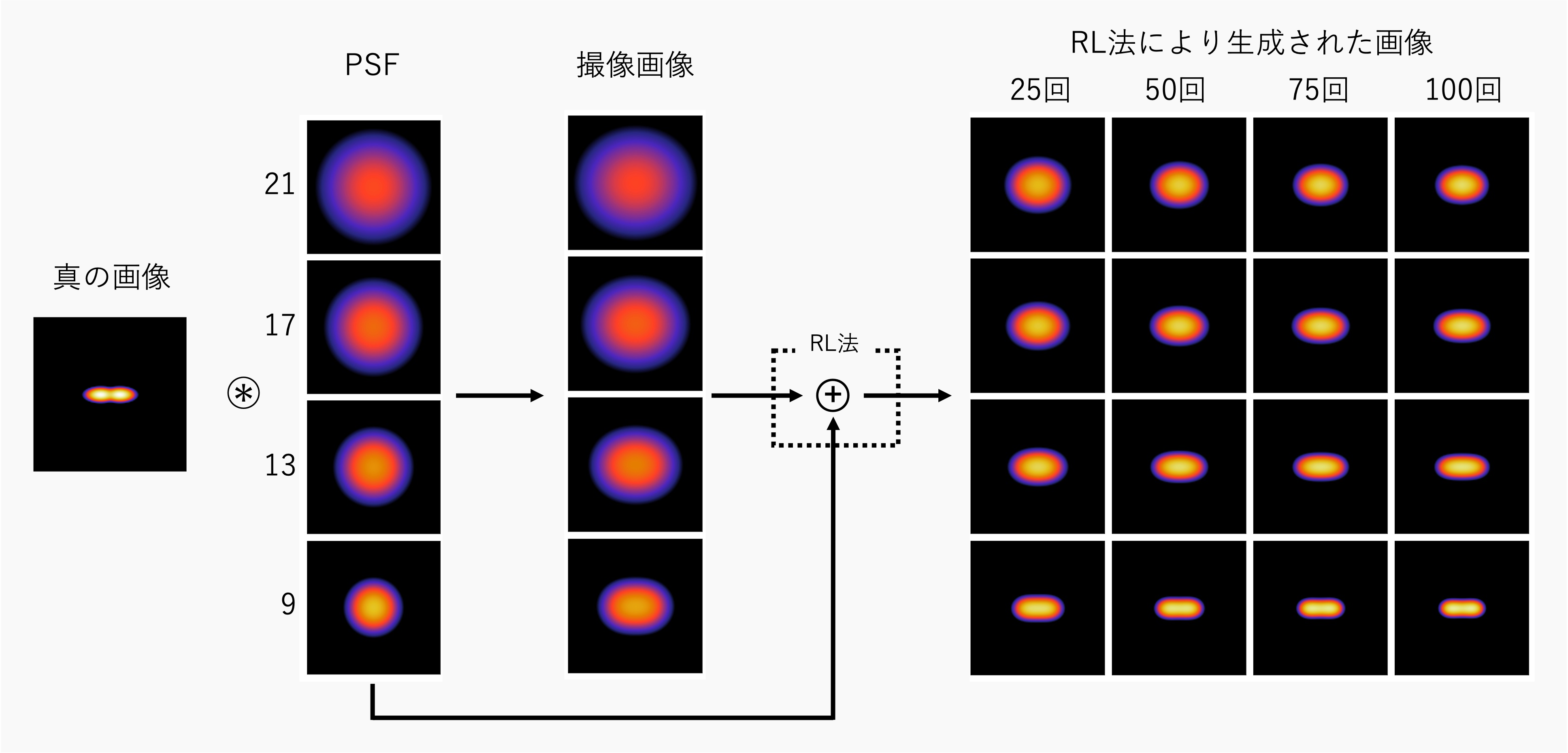
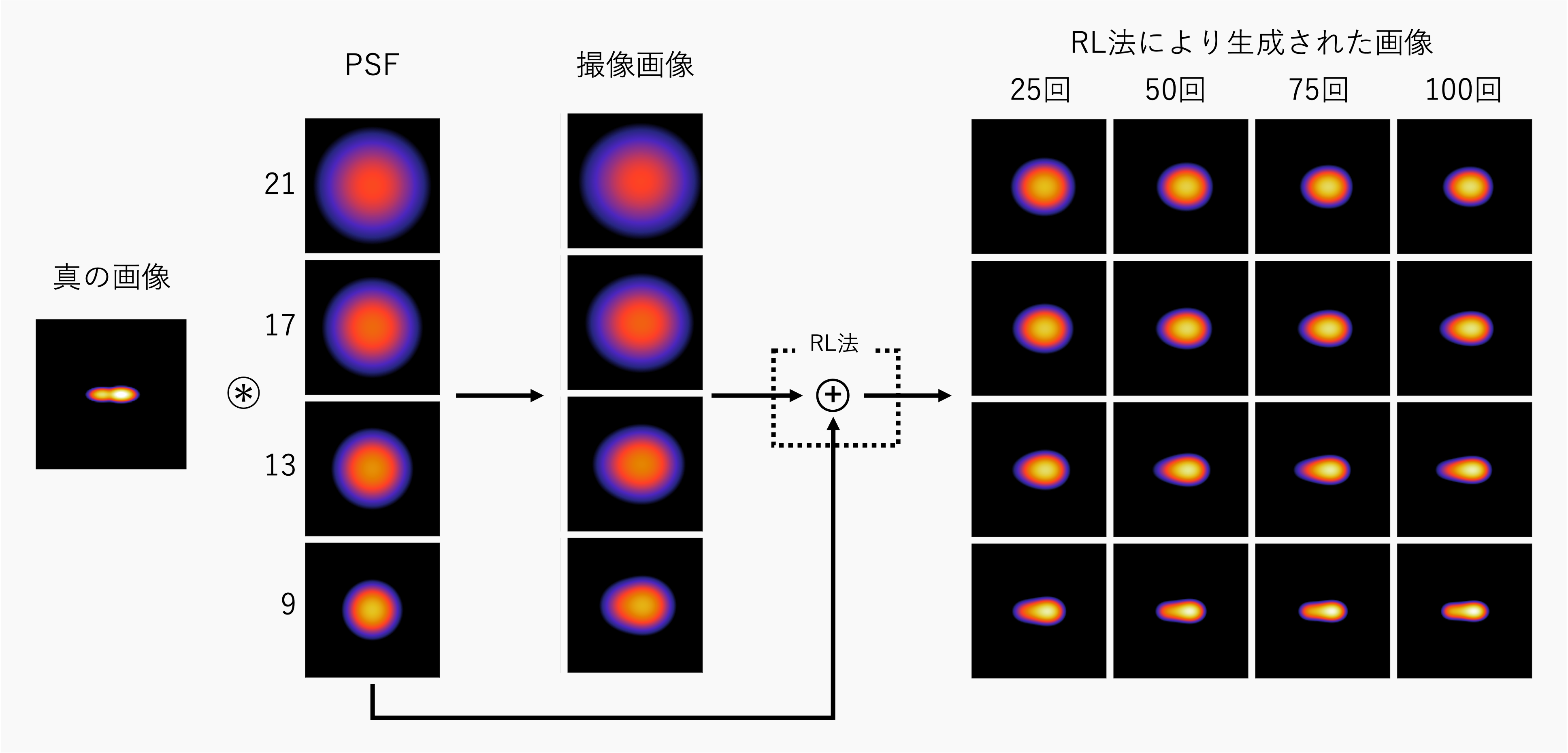
反復回数を変化させる

  • 反復回数5, 10, 15, 20回の結果
    図1.png
  • 反復回数25, 50, 75, 100回の結果
    図1.png

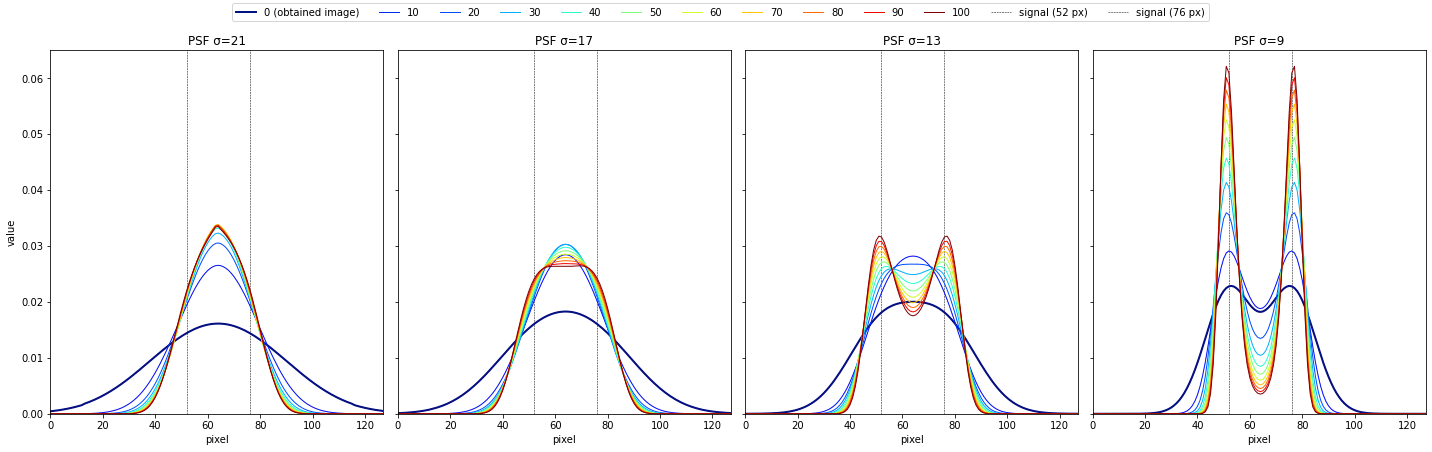
このように、反復回数が大きくなるにつれて、真の画像に近づくことが分かる。また、反復回数が5~20回では、25~100回に比べて急激に画像が変化していることが分かる。

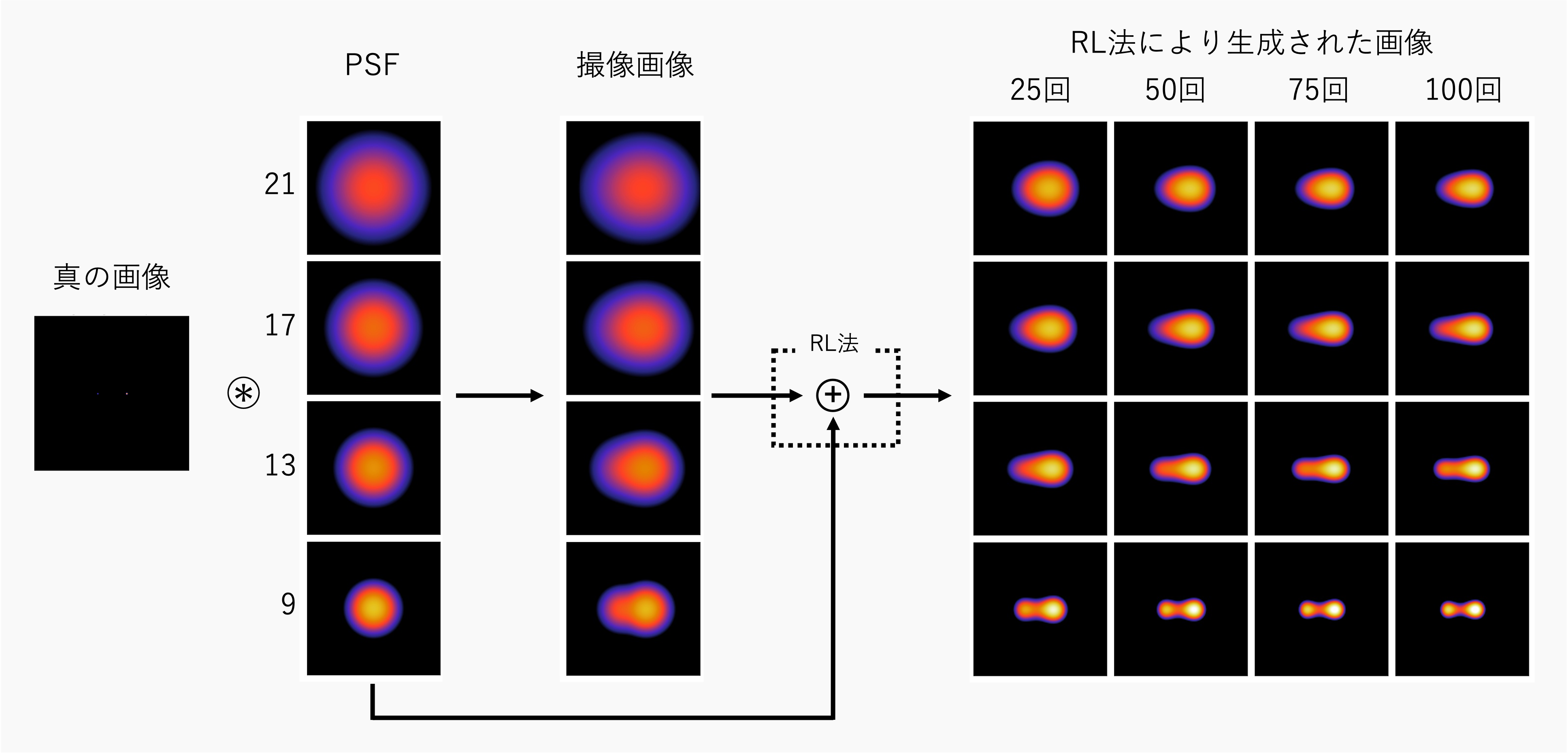
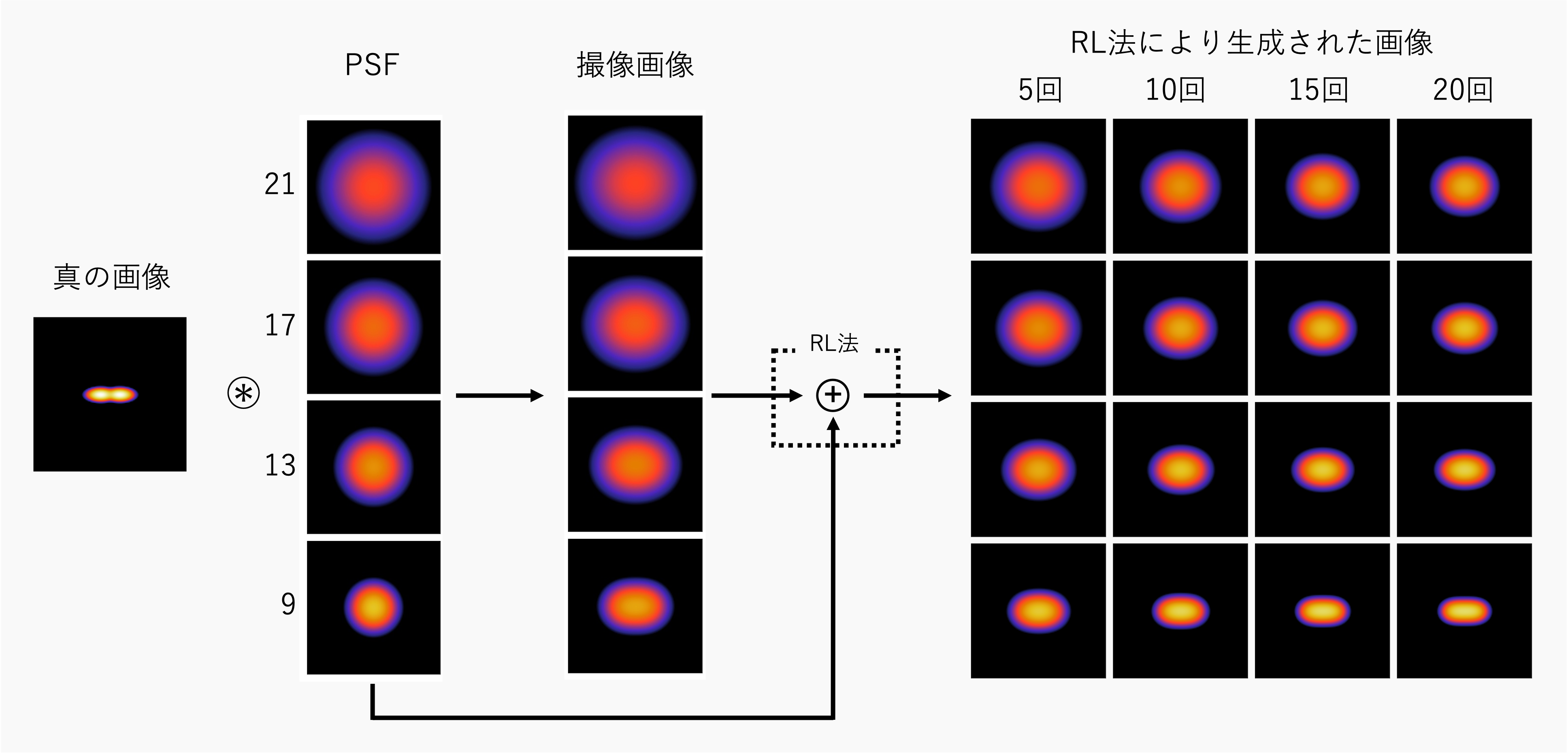
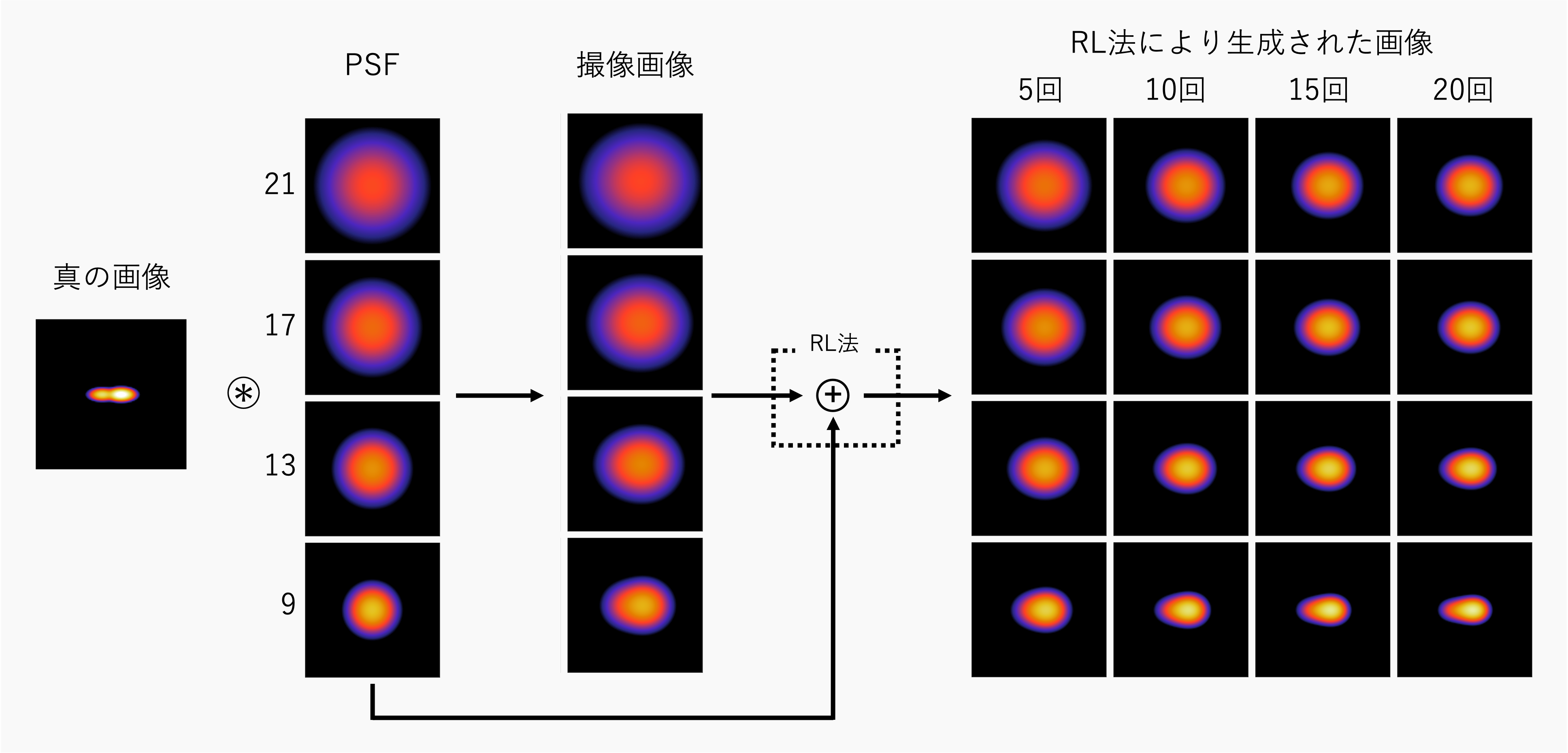
PSFを変化させる

  • psf_sigma=21, 17, 13, 9で、反復回数5, 10, 15, 20回の結果
    図2.png

  • psf_sigma=21, 17, 13, 9で、反復回数25, 50, 75, 100回の結果
    図3.png

このように、PSFが小さいほど、同じ反復回数で比べたときに真の画像に近いことが分かる。

色々なサンプルでシミュレーション

RL法の特徴を理解するために、偏りのある点源の場合、点源が適当に散らばった場合、拡がった構造の場合、偏りのある拡がった構造の場合でシミュレーションする。

偏りのある点源の場合

偏りのある点源の場合（真の画像のコード部分）
"""シミュレーション"""
# 真の画像
true_px = 128
true_img = np.zeros([true_px, true_px])
true_img[64, 52] = 0.2
true_img[64, 76] = 0.8
"""以下省略"""

RL法のシミュレーションのコードの、真の画像を変更している。

  • 出力結果
    image.png

  • psf_sigma=21, 17, 13, 9で、反復回数5, 10, 15, 20回の結果
    図4.png

  • psf_sigma=21, 17, 13, 9で、反復回数25, 50, 75, 100回の結果
    図5.png

このように、大きい値（明るい）の点源によって小さい値（暗い）の点源が見えにくくなることが分かる。ただ、PSFが小さい場合は反復回数を増やすことで、それぞれの点源に見分けられている。

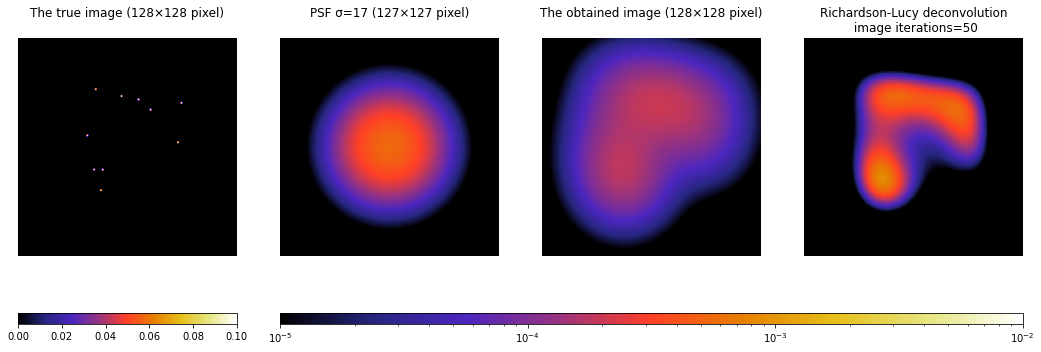
適当に散らばった点源の場合

適当に散らばった点源の場合（真の画像のコード部分）
"""シミュレーション"""
# 真の画像
true_px = 128
true_img = np.zeros([true_px, true_px])
true_img[77, 44] = 0.1
true_img[34, 60] = 0.1
true_img[77, 49] = 0.1
true_img[61, 93] = 0.1
true_img[57, 40] = 0.1
true_img[38, 95] = 0.1
true_img[89, 48] = 0.1
true_img[36, 70] = 0.1
true_img[30, 45] = 0.1
true_img[42, 77] = 0.1
"""以下省略"""

RL法のシミュレーションのコードの、真の画像と真の画像のカラーバーの最大値を0.1に変更している。
※適当に散らばった点源のピクセル座標はPythonの疑似乱数（random）により生成しているが、本題とは関係が薄いためコードを割愛する。

  • 出力結果
    image.png

  • psf_sigma=21, 17, 13, 9で、反復回数5, 10, 15, 20回の結果
    図6.png

  • psf_sigma=21, 17, 13, 9で、反復回数25, 50, 75, 100回の結果
    図7.png

このように、PSFが小さいほど見分けられる構造が増えることが分かる。また、RL法を行った方が見分けられる構造が増えるとことも分かる。

拡がった構造の場合

拡がった構造の場合（真の画像のコード部分）
"""シミュレーション"""
# 真の画像
true_px = 128
true_half_px = true_px // 2
x, y = np.mgrid[-true_half_px:true_half_px:, -true_half_px:true_half_px:]
pos = np.dstack((x, y))
rv1 = multivariate_normal([0, -8], [[4, 0], [0, 18]])
rv2 = multivariate_normal([0, 8], [[4, 0], [0, 18]])
true_img = 0.5*rv1.pdf(pos) + 0.5*rv2.pdf(pos)
"""以下省略"""

RL法のシミュレーションのコードの、真の画像と真の画像のカラーバーの表示形式を対数に変えている。

  • 出力結果
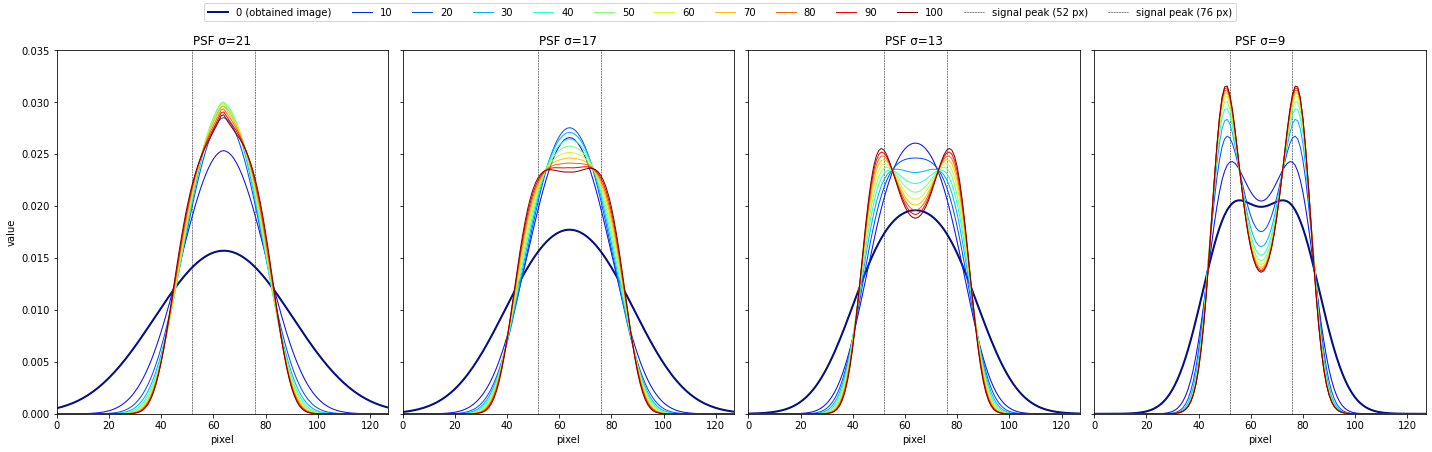
    image.png

  • psf_sigma=21, 17, 13, 9で、反復回数5, 10, 15, 20回の結果
    図8.png

  • psf_sigma=21, 17, 13, 9で、反復回数25, 50, 75, 100回の結果
    図9.png

このように、点源のときと同様PSFが小さいほど、同じ反復回数で比べたときに真の画像に近いことが分かる。
また、PSFよりも小さい領域ではPSFを変化させると似た形がRL法で得られることが分かる。このことから、PSFの拡がりよりも小さい領域において、RL法では点源なのか拡がった構造なのか見分けることが困難であると考えられる。

偏りのある拡がった構造の場合

偏りのある拡がった構造の場合（真の画像のコード部分）
"""シミュレーション"""
# 真の画像
true_px = 128
true_half_px = true_px // 2
x, y = np.mgrid[-true_half_px:true_half_px:, -true_half_px:true_half_px:]
pos = np.dstack((x, y))
rv1 = multivariate_normal([0, -8], [[4, 0], [0, 18]])
rv2 = multivariate_normal([0, 8], [[4, 0], [0, 18]])
true_img = 0.2*rv1.pdf(pos) + 0.8*rv2.pdf(pos)
"""以下省略"""

RL法のシミュレーションのコードの、真の画像と真の画像のカラーバーの表示形式を対数に変えている。

  • 出力結果
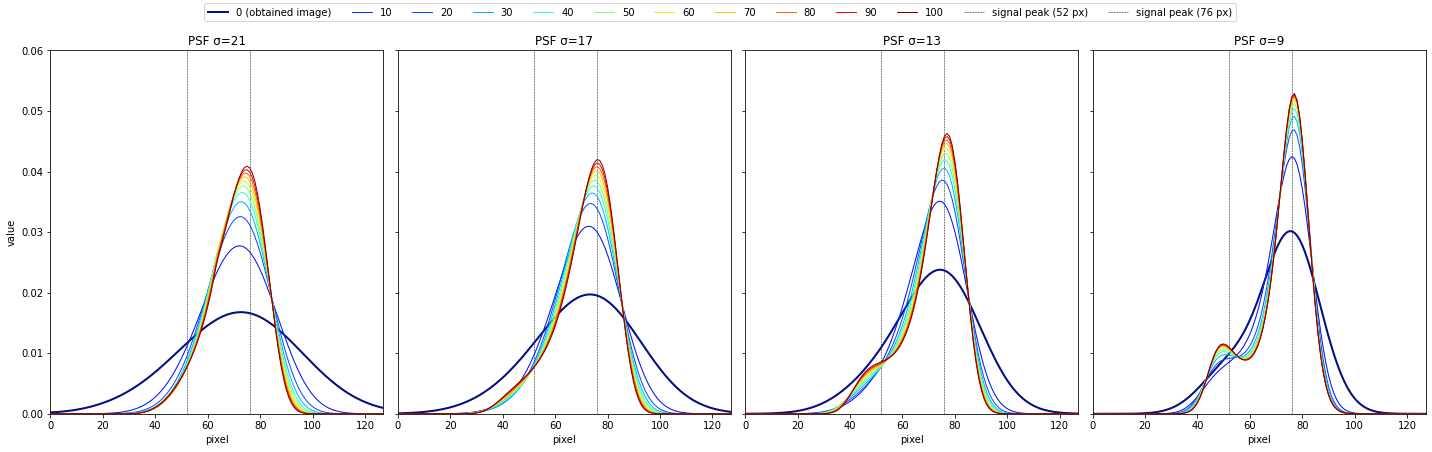
    image.png

  • psf_sigma=21, 17, 13, 9で、反復回数5, 10, 15, 20回の結果
    図10.png

  • psf_sigma=21, 17, 13, 9で、反復回数25, 50, 75, 100回の結果
    図11.png

このように、点源のときと同様大きい値（明るい）の構造によって小さい値（暗い）の構造が見えにくくなることが分かる。ただ、PSFが小さい場合は反復回数を増やすことで、それぞれの点源に見分けられている。
また、PSFよりも小さい領域では偏りのある点源の場合と似た形がRL法で得られることが分かる。このことから、PSFの拡がりよりも小さい領域において、RL法では点源なのか拡がった構造なのか見分けることが困難であると考えられる。

1次元でのRL法のシミュレーションの実装（おまけ）

1次元でのRL法のシミュレーションの実装についても簡単に紹介する。
基本的なコードは2次元の場合と同じである。ただ、1次元のPSFは正規分布（SciPyのnorm）を使い、2次元のときのような高級な多変量正規分布は使わずに実装する。

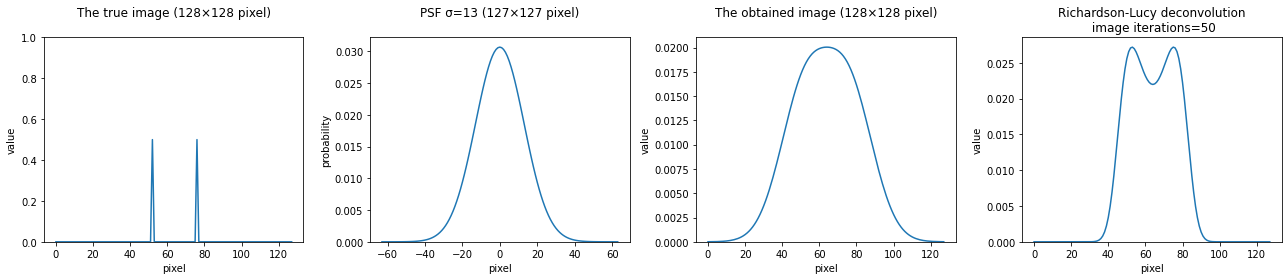
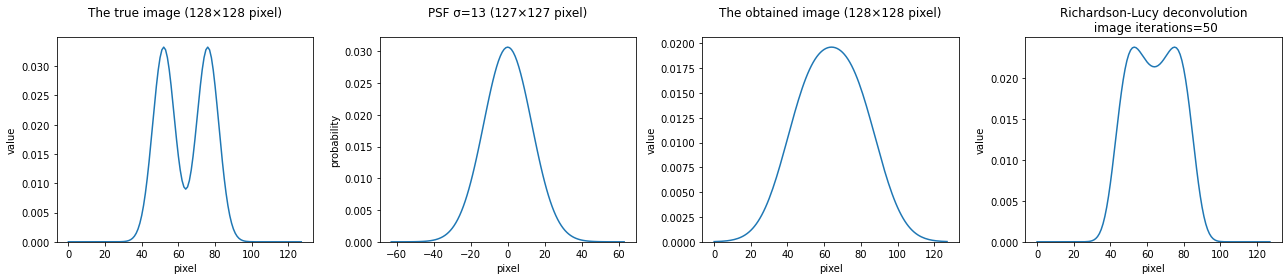
点源の場合

RL法のシミュレーション（1次元バージョン）
"""シミュレーション（1次元バージョン）"""
# 真の画像
true_px = 128
true_img = np.zeros(true_px)
true_img[52] = 0.5
true_img[76] = 0.5

# PSF
psf_px = 127
mean = psf_px // 2
psf_sigma = 13
psf = norm.pdf(np.arange(psf_px), loc=mean, scale=psf_sigma)

# 真の画像をPSFで畳み込む（撮像画像）
obtained_img = convolve(true_img, psf, "same")

# RL法
iterations = 50
rl_img = restoration.richardson_lucy(obtained_img, psf, iterations)

"""シミュレーションの結果を図に表示"""
fig, (ax1, ax2, ax3, ax4) = plt.subplots(figsize=(18, 4), ncols=4)

# 真の画像
ax1.set_title("The true image ({0}×{0} pixel)\n".format(true_px))
ax1.plot(true_img)
ax1.set_xlabel("pixel")
ax1.set_ylabel("value")
ax1.set_ylim(0, 1)

# PSF
ax2.set_title("PSF σ={0} ({1}×{1} pixel)\n".format(psf_sigma, psf_px))
ax2.plot(np.arange(-63, 64, 1), psf)
ax2.set_xlabel("pixel")
ax2.set_ylabel("probability")
ax2.set_ylim(bottom=0)

# 撮像画像
ax3.set_title("The obtained image ({0}×{0} pixel)\n".format(true_px))
ax3.plot(obtained_img)
ax3.set_xlabel("pixel")
ax3.set_ylabel("value")
ax3.set_ylim(bottom=0)

# RL法による生成画像
ax4.set_title("Richardson-Lucy deconvolution\n image iterations={0}".format(iterations))
ax4.plot(rl_img)
ax4.set_xlabel("pixel")
ax4.set_ylabel("value")
ax4.set_ylim(bottom=0)

fig.tight_layout()
plt.show()

  • 出力結果
    image.png

  • コードの概念図
    図1.png

  • psf_sigma=21, 17, 13, 9で、反復回数10~100回の結果
    次図を作成したコードは、本題とは関係が薄いためここでは割愛してGoogle Colab内こちらで紹介する。
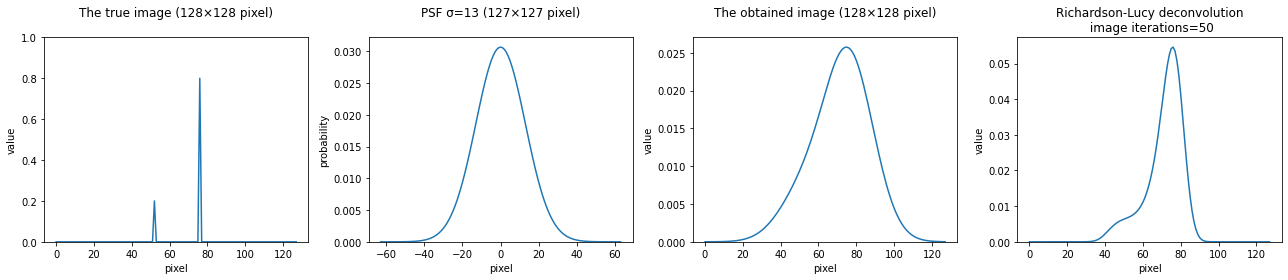
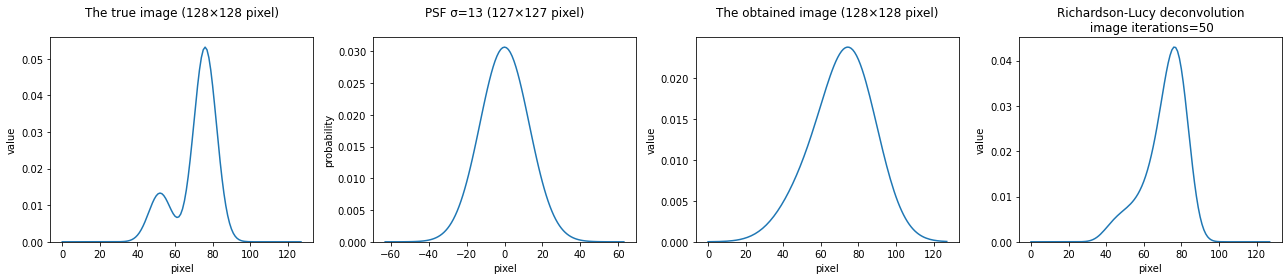
    image.png

偏りのある点源の場合

偏りのある点源の場合（真の画像のコード部分）
"""シミュレーション（1次元バージョン）"""
# 真の画像
true_px = 128
true_img = np.zeros(true_px)
true_img[52] = 0.2
true_img[76] = 0.8
"""以下省略"""

  • 出力結果
    image.png

  • psf_sigma=21, 17, 13, 9で、反復回数10~100回の結果
    次図を作成したコードは、本題とは関係が薄いためここでは割愛してGoogle Colab内こちらで紹介する。
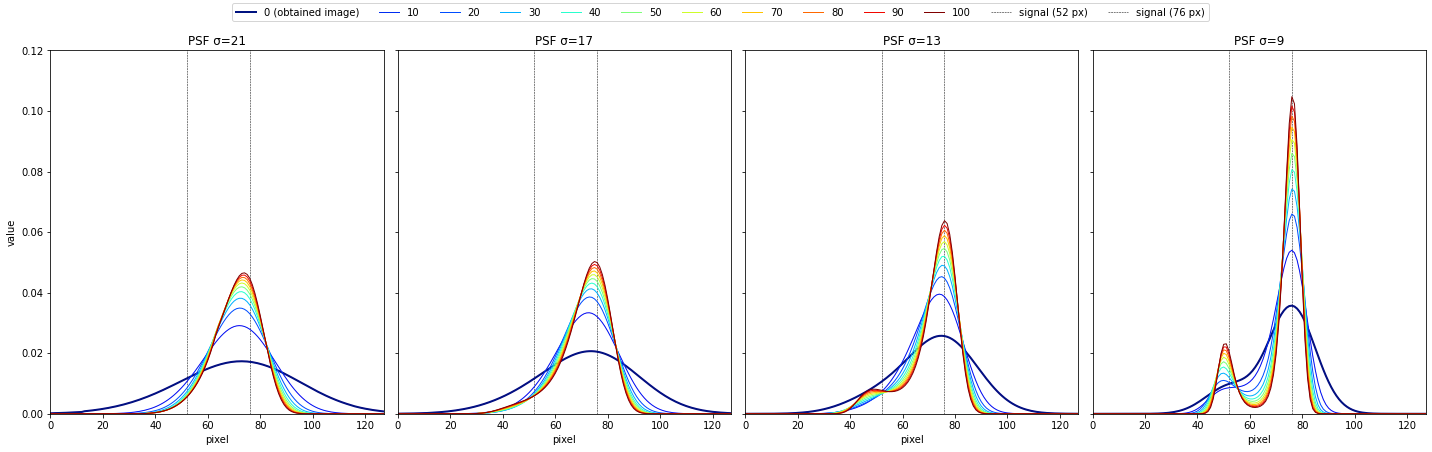
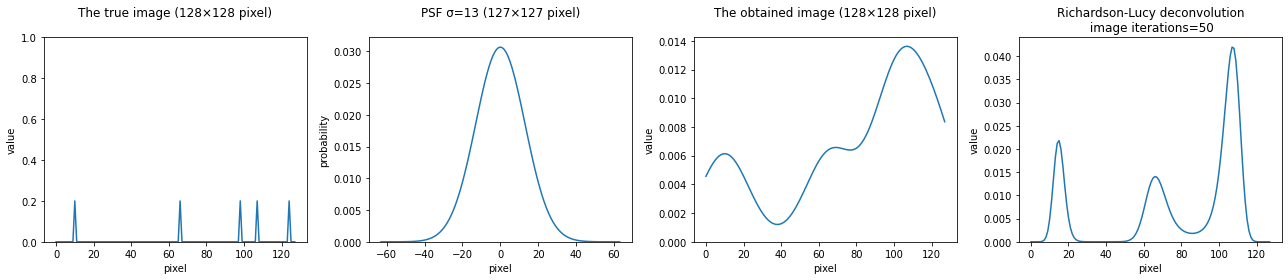
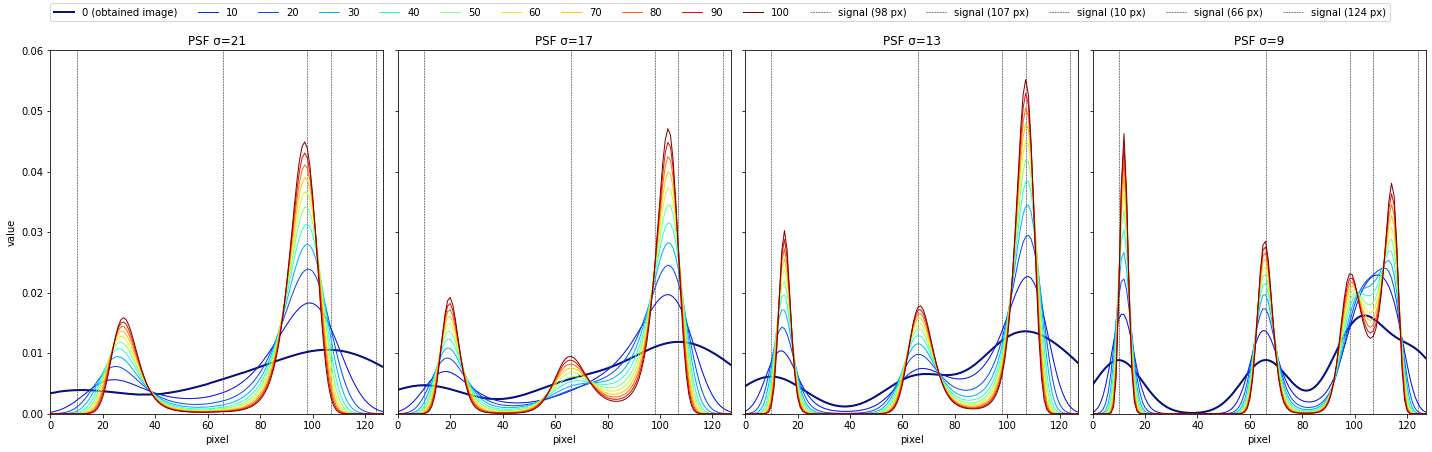
    image.png

適当に散らばった点源の場合

適当に散らばった点源の場合（真の画像のコード部分）
"""シミュレーション（1次元バージョン）"""
# 真の画像
true_px = 128
true_img = np.zeros(true_px)
true_img[98] = 0.2
true_img[107] = 0.2
true_img[10] = 0.2
true_img[66] = 0.2
true_img[124] = 0.2
"""以下省略"""

※適当に散らばった点源のピクセル座標はPythonの疑似乱数（random）により生成しているが、本題とは関係が薄いためコードを割愛する。

  • 出力結果
    image.png

  • psf_sigma=21, 17, 13, 9で、反復回数10~100回の結果
    次図を作成したコードは、本題とは関係が薄いためここでは割愛してGoogle Colab内こちらで紹介する。
    image.png

拡がった構造の場合

拡がった構造の場合（真の画像のコード部分）
"""シミュレーション（1次元バージョン）"""
# 真の画像
true_px = 128
signal_1 = norm.pdf(np.arange(true_px), loc=52, scale=6)
signal_2 = norm.pdf(np.arange(true_px), loc=76, scale=6)
true_img = 0.5*signal_1 + 0.5*signal_2
"""以下省略"""

  • 出力結果
    image.png

  • psf_sigma=21, 17, 13, 9で、反復回数10~100回の結果
    次図を作成したコードは、本題とは関係が薄いためここでは割愛してGoogle Colab内こちらで紹介する。
    image.png

偏りのある拡がった構造の場合

偏りのある拡がった構造の場合（真の画像のコード部分）
"""シミュレーション（1次元バージョン）"""
# 真の画像
true_px = 128
signal_1 = norm.pdf(np.arange(true_px), loc=52, scale=6)
signal_2 = norm.pdf(np.arange(true_px), loc=76, scale=6)
true_img = 0.2*signal_1 + 0.8*signal_2
"""以下省略"""

  • 出力結果
    image.png

  • psf_sigma=21, 17, 13, 9で、反復回数10~100回の結果
    次図を作成したコードは、本題とは関係が薄いためここでは割愛してGoogle Colab内こちらで紹介する。
    image.png

まとめ

真の画像とPSFが完全にわかっていて、かつノイズが乗らない理想的な状況でのシミュレーションにより、わかったことを以下にまとめる。

  • RL法により得られた画像は、撮像画像と比べて真の画像に近いことがわかった。
  • RL法の反復回数が5~20回で得られる画像は、25回以上で得られる画像よりも急激に画像が変化していた。
  • RL法の反復回数が多くなるにつれて、真の画像により近い画像が得られた。
  • PSFが小さいほど、RL法を行ったときに見分けられる部分が増えた（真の画像に近い画像が得られた）。
  • 点源と拡がった構造のシミュレーションの結果、PSFの拡がりよりも小さい領域では似たようなイメージが得られた。
    このことから、RL法はPSFよりもある程度小さい領域では、そこに点源なのか拡がった構造が存在するのか見極めることが困難であると考えられる。

中編ではRL法の結果をもう少し深掘りする予定である。

参考文献

  • Richardson, William Hadley. 1972, JOSA, 62, 55–59
  • Lucy, L. B. 1974, Astronomical Journal, 79, 745–754

関連資料

8
9
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
9