はじめに
多変量正規分布の様々な性質を明らかにしていきます。プロットしやすいことから、主に2変量正規分布を扱います。主成分分析、固有値分解、特異値分解などにも触れていきます。
2変量正規分布の基本情報
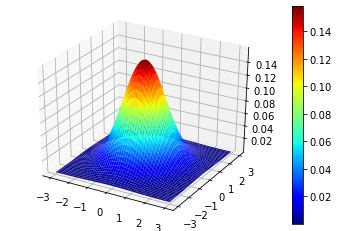
2変量正規分布の密度関数は下式で与えられます。
f(\boldsymbol{x};\boldsymbol{\mu},\Sigma) = \frac{1}{2\pi |\Sigma|}\exp
\Bigl\{
-\frac{1}{2}{(\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}}(\boldsymbol{x}-\boldsymbol{\mu})\Bigr\}\\
ただし、
\boldsymbol{x}=
\begin{pmatrix}
x_1\\
x_2
\end{pmatrix},
\boldsymbol{\mu}=
\begin{pmatrix}
\mu_1\\
\mu_2
\end{pmatrix},
\Sigma =
\begin{pmatrix}
s_{11} & s_{12}\\
s_{21} & s_{22}
\end{pmatrix}
です。
例えば、
\boldsymbol{\mu}=
\begin{pmatrix}
0\\
0
\end{pmatrix},
\Sigma =
\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}
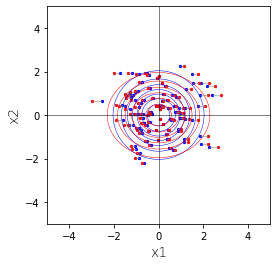
として、密度関数の図示すると下のようになります。
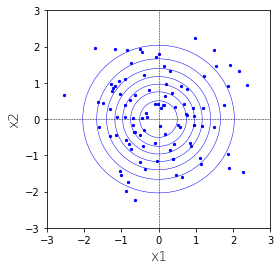
上記の確率分布から発生させた100サンプルと密度関数の等高線を図示すると下のようになります。
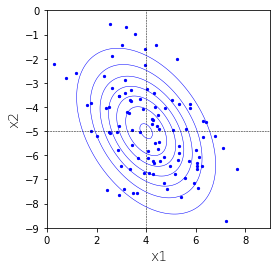
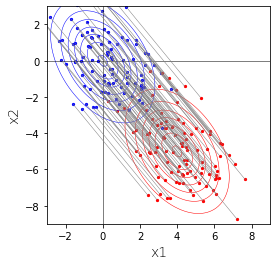
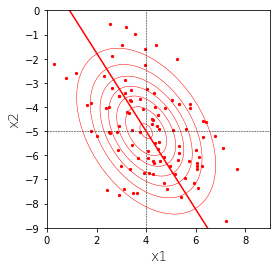
$\boldsymbol{\mu},\Sigma$を変更することで分布は様々な形をとります。例えば、
\boldsymbol{\mu}=
\begin{pmatrix}
4\\
-5
\end{pmatrix},
\Sigma =
\begin{pmatrix}
2 & -1\\
-1 & 3
\end{pmatrix}
とすると、
となります。
正規分布はどこから見ても正規分布
例1
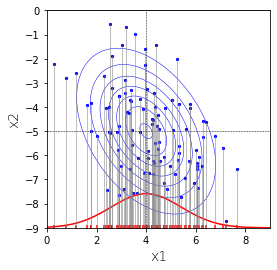
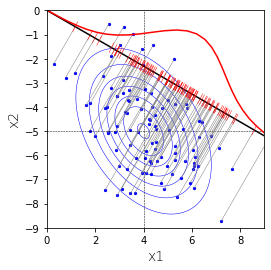
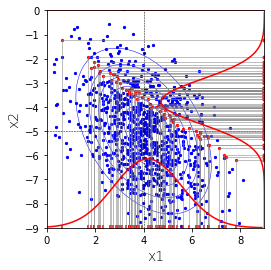
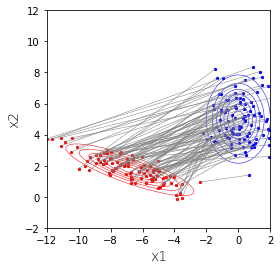
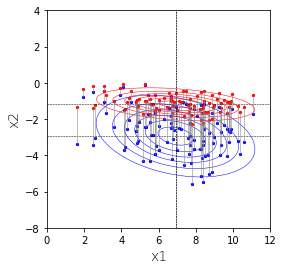
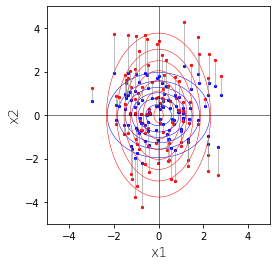
下図の正規分布を下方向から上に向かってみてみます。青色の点を直線$x_2=-9$に射影することと同じことです。
その結果が下図の赤色です。この赤は1変量の正規分布になります。
例2
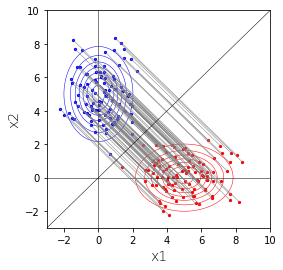
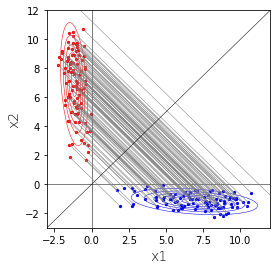
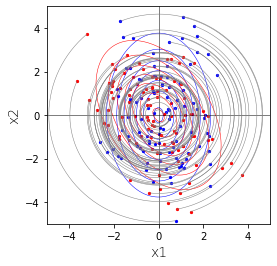
見る方向を変えてみます。青色の点を直線$x_2=-\frac{1}{\sqrt{3}}x_1$に射影しています。
この赤の分布は1変量の正規分布になります。
例3
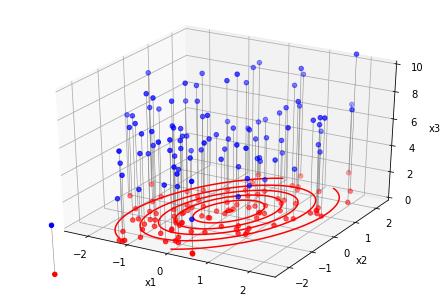
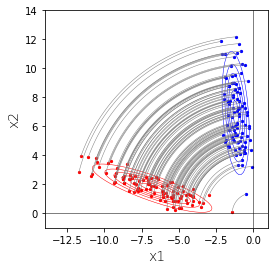
3変量の正規分布を2次元空間に射影してみます。
\boldsymbol{\mu}=
\begin{pmatrix}
0\\
0\\
6
\end{pmatrix},
\Sigma =
\begin{pmatrix}
1 & \frac{1}{2} & -\frac{1}{2}\\
-\frac{1}{2} & 2 & 1\\
-\frac{1}{2} & 1 & 3
\end{pmatrix}
として、発生させた3変量正規分布からのサンプルを2次元平面$x_3=0$に射影したのが下図です。
赤は2変量の正規分布に従います。
正規分布はどの断面を見ても正規分布
例1
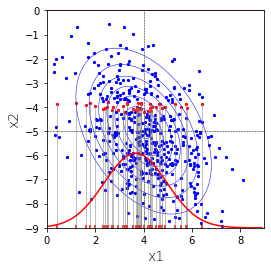
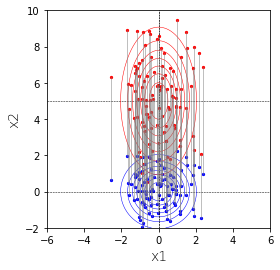
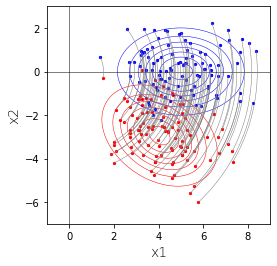
2変量の正規分布のうち、$x_2=-4$付近のもの(赤)だけを取り出します。赤は1変量の正規分布になります。
例2
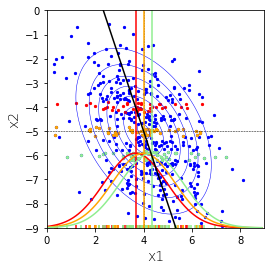
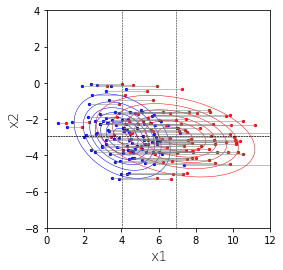
例1と同様に、$x_2=-4$付近のもの(赤)、$x_2=-5$付近のもの(オレンジ)、$x_2=-4$付近のもの(薄緑)だけを取り出します。
それぞれ1変量の正規分布になります。3つの正規分布の分散は同じです。平均は黒直線に従い動きます。
例3
$x_1$,$x_2$軸に沿っていない断面をとってみます。下図は$x_2=-\frac{2}{3}-1$に沿って切った断面の図です。
この赤も正規分布となります。
尚、3変量以上の正規分布についても断面をとると正規分布になります。
正規分布の線形変換は正規分布
例1
$\boldsymbol{X}$が平均$\boldsymbol{\mu}$、分散$\Sigma$の正規分布に従うとき、$A\boldsymbol{X} + \boldsymbol{b}$は、平均$A\boldsymbol{\mu} + \boldsymbol{b}$、分散$A^T\Sigma A$の正規分布に従います。
例えば、
\boldsymbol{X}=\begin{pmatrix}
X_1\\
X_2
\end{pmatrix}
を下図の青の分布として、
A =
\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix},\boldsymbol{b}=\begin{pmatrix}
2\\
3
\end{pmatrix}
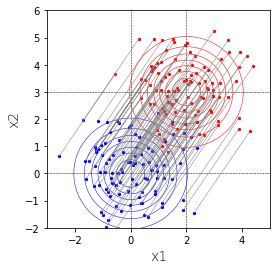
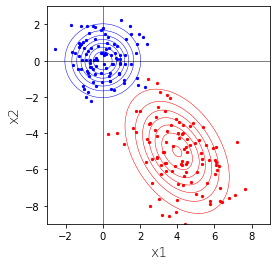
とすると、$A\boldsymbol{X} + \boldsymbol{b}$は赤の分布となります。これは正規分布です。
青に対して、$x_1$軸に沿って+2、$x_2$軸に沿って+3平行移動するイメージです。
例2
A =
\begin{pmatrix}
1 & 0\\
0 & 2
\end{pmatrix},\boldsymbol{b}=\begin{pmatrix}
0\\
5
\end{pmatrix}
としてみます。$\boldsymbol{X}$を青の分布とすると、$A\boldsymbol{X} + \boldsymbol{b}$は赤の分布となります。これは正規分布です。
青に対して、$x_2$軸方向に2倍引き伸ばし、$x_2$軸に沿って+5平行移動するイメージです。
例3
A =
\begin{pmatrix}
\cos\theta_0 & -\sin\theta_0\\
\sin\theta_0 & \cos\theta_0
\end{pmatrix}
,\boldsymbol{b}=\begin{pmatrix}
0\\
0
\end{pmatrix}
としてみます(ただし、$\theta_0=\pi/3=$60[度]としました)。$\boldsymbol{X}$を青の分布とすると、$A\boldsymbol{X} + \boldsymbol{b}$は赤の分布となります。これは正規分布です。
原点を中心に60[度]回転するイメージです。
例4
Aがきれいでない場合について見てみます。
A =
\begin{pmatrix}
-\frac{\pi}{4} & -\frac{e}{2}\\
\frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{5}
\end{pmatrix}
,\boldsymbol{b}=\begin{pmatrix}
0\\
0
\end{pmatrix}
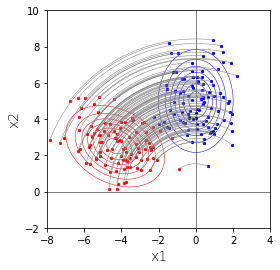
としてみます。$\boldsymbol{X}$を青の分布とすると、$A\boldsymbol{X} + \boldsymbol{b}$は赤の分布となります。これは正規分布です。
これがどういう変換かは、$A$を分解することで見えてきます。
A =
\begin{pmatrix}
-\frac{\pi}{4} & -\frac{e}{2}\\
\frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{5}
\end{pmatrix}
=
\begin{pmatrix}
\cos\theta_0 & -\sin\theta_0\\
\sin\theta_0 & \cos\theta_0
\end{pmatrix}
\begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix}
\begin{pmatrix}
1 & 0\\
0 & \lambda_2
\end{pmatrix}
\begin{pmatrix}
\lambda_1 & 0\\
0 & 1
\end{pmatrix}
\begin{pmatrix}
\cos\theta_1 & -\sin\theta_1\\
\sin\theta_1 & \cos\theta_1
\end{pmatrix}
\begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix}
ただし、$\theta_0$=65.97[度]、$\theta_1=$-36.02[度]、$\lambda_1=$1.71、$\lambda_2$=0.40です。
このことから、$A\boldsymbol{X} + \boldsymbol{b}$は$\boldsymbol{X}$に対して、下の1.~6.の変換を施したものであることがわかります。これらの変換では正規分布特有の釣り鐘の形は崩れません。よって、変換後も正規分布になります。
- $x_1$と$x_2$を反転
- -36.02[度]回転
- $x_1$軸方向に1.71倍する(引き伸ばす)
- $x_2$軸方向に0.40倍する(縮める)
- $x_1$と$x_2$を反転
- 65.97[度]回転
- 1.の変換の図
- 2.の変換の図
- 3.の変換の図
- 4.の変換の図
- 5.の変換の図
- 6.の変換の図
参考
行列のAの分解は、特異値分解によりできます。下は特異値分解のpythonソースコードです。
import numpy as np
A = np.array([[-np.pi/4, - np.exp(1)/2],
[np.sqrt(2)/2, np.sqrt(3)/5]])
a, b, c = np.linalg.svd(A)
print(a)
# [[-0.913335 0.40720901]
# [ 0.40720901 0.913335 ]]
print(b)
# [1.70927919 0.40308678]
print(c)
# [[ 0.58812621 0.80876917]
# [ 0.80876917 -0.58812621]]
任意の正規分布は標準正規分布の線形変換で作成できる
例1
\boldsymbol{\mu}=
\begin{pmatrix}
0\\
0
\end{pmatrix},
\Sigma =
\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}
としたときの正規分布は下図青です。
\boldsymbol{\mu}=
\begin{pmatrix}
4\\
-5
\end{pmatrix},
\Sigma =
\begin{pmatrix}
2 & -1\\
-1 & 3
\end{pmatrix}
としたときの正規分布は下図赤です。
青の分布$\boldsymbol{X}$ に対して、
A =
\begin{pmatrix}
\cos\theta & -\sin\theta\\
\sin\theta & \cos\theta
\end{pmatrix}
\begin{pmatrix}
\lambda_1 & 0\\
0 & \lambda_2
\end{pmatrix},
\boldsymbol{b}=
\begin{pmatrix}
4\\
-5
\end{pmatrix}
とすると、$A\boldsymbol{X}+b$は赤の分布になります。ただし、$\theta=$-148.28[度]、$\lambda_1$=1.176、$\lambda_2$=1.902 です。
以上から、青色の分布に対して、以下の変換を加えると赤色の分布になることがわかります。
- $x_1$軸方向に1.176倍引き伸ばす
- $x_2$軸方向に1.902倍引き伸ばす
- -148.28[度]回転させる
- $x_1$軸に沿って+4,$x_2$軸に沿って-5平行移動させる
- 1.の変換の図
- 2.の変換の図
- 3.の変換の図
- 4.の変換の図
参考1
Aの導出は固有値分解により求めることができます。下は固有値分解のpythonソースコードです。
import numpy as np
sigma = np.array([[2, -1], [-1, 3]])
u, v = np.linalg.eig(sigma)
print(np.sqrt(u))
# [1.1755705 1.90211303]
print(v)
# [[-0.85065081 0.52573111]
# [-0.52573111 -0.85065081]]
参考2
等高線の長軸が、$(x_1,x_2)=(4,-5)$を通り、傾きが$x_2$軸を起点として-148.28[度]の直線となることが上の1.~4.の変換から分かります。
これは主成分分析の第一主成分の軸です。主成分分析は正規分布の密度関数の等高線の楕円の軸を見つけることに相当します。参考1によると、楕円の軸を見つけるためには、分散に対して固有値分解をすればよいことがわかります。