なぜジェットは光より速く見えるのか：Pythonで考える超光速運動

はじめに

天体物理でよく話題になる「超光速運動 (superluminal motion)」──
「ジェットが光速を超えて動いているように見える」現象です。

もちろん、実際に光速を超えているわけではありません。
その正体は、光の到達時間 (light-travel time) の効果によって、観測者に届く光が時間的に圧縮されて見えることにあります。

この効果が理論的に指摘されたのは 1960 年代に遡り、1970 年代の VLBI 観測でクエーサーや活動銀河核 (AGN) のジェットにおいて実際に超光速運動が報告され、「相対論的ジェットの特徴」として定着しました。

光行時間の影響は、光速の数十％で動くジェット（mildly relativistic jets）でも効いてきます。その代表的な天体として、筆者が少し研究している SS 433 のジェット（光速の約 26%）も、この効果を無視すると観測画像で見える動きが少しずれてしまいます。

この記事では、

• 超光速運動の数式をステップごとに導出
• Python でパラメータ空間を可視化
• 歳差運動ジェット SS 433 を例に見かけ速度をマッピング

を通じて、この現象を直感的に理解していきます。

（筆者自身もまだ学びながら整理している段階なので、同じく学んでいる方にも楽しんでもらえるコンテンツを目指しています。
記事中の誤りや改善点、面白い可視化のアイデア、構成の工夫、実際の解析での応用例なども、ぜひコメントで教えていただけると嬉しいです！）

実装コードは Google Colab こちら から自由に動かせます。ぜひ遊んでみててください。

超光速運動の導出

1. 設定

• 物体が速度 $v = \beta c$ で運動する
• 観測者から見た視線方向とのなす角度を $\theta$ とする
• 観測者は十分遠方にいると仮定し、平行光近似が成り立つとする

このとき観測者は、2つの時刻で放射された光シグナルの到着時間差を比較して運動を評価します。

---

2. 物体の進み方

時間 $\Delta t$ の間に ejecta が進む距離を、視線方向の成分と垂直成分に分解します：

d_\parallel = v \, \Delta t \cos\theta, \quad
d_\perp = v \, \Delta t \sin\theta

ここで $d_\perp$ が「空に投影された見かけの動き」になります。

ポンチ絵で表すと以下のようになります。

この図からわかるように、発光点が横方向に光を出すよりも、少しこちらに向かって動きながら光を出した方が、観測者にはより早く光が届きます。
つまり「前に寄ることで時間を稼ぐ効果」が生じ、見かけ上の速度が増すのがポイントです。

（詳細は後ほど数式で確認しますので、この段階では「そういう効果があるんだな」程度で大丈夫です）

---

3. 観測される時間差

光が観測者に届くまでの遅延を考えると、2つのシグナルの到着時間差は：

\Delta t_{\rm obs} = \Delta t - \frac{d_\parallel}{c}
= \Delta t - \frac{v \Delta t \cos\theta}{c}
= \Delta t (1 - \beta \cos\theta)

ここで「垂直方向の進み ($d_\perp$)」は観測者までの距離にほとんど影響を与えない（無限遠を仮定しているため）ので、近似的に無視できます。

---

4. 見かけの速度

見かけの速度は「投影された距離 / 観測時間差」：

v_{\rm app} = \frac{d_\perp}{\Delta t_{\rm obs}}
= \frac{v \sin\theta \, \Delta t}{\Delta t (1 - \beta \cos\theta)}
= \frac{v \sin\theta}{1 - \beta \cos\theta}

---

5. 見かけ速度の無次元化

光速で割ると、見かけの速度の式が得られます：

\boxed{\beta_{\rm app} = \frac{\beta \, \sin\theta}{1 - \beta \cos\theta}}\tag{*}

ここでの定義は以下の通りです：

• 速度は $0 \leq \beta < 1$

• 角度は $0^\circ \leq \theta \leq 180^\circ$

  • $\theta=0^\circ$: 観測者に向かう
  • $\theta=90^\circ$: 横方向
  • $\theta=180^\circ$: 観測者から遠ざかる

この式は今後繰り返し登場するため、以降は式（*）として参照します。

直感的な理解

ポイントは視線垂直方向の運動に対してどれくらい時間を稼げるかにあります。

• 真横（θ=90°）
  このときは $\beta_{\rm app} = \beta$ となり、真の速度がそのまま見かけの速度に見えます。

• 前寄り（θ < 90°）
  光の到達時間短縮が効くため、観測者は「より進んだ位置の情報」に早くアクセスできます。
  その結果、見かけの速度が大きくなります。

• 後寄り（θ > 90°）
  光の到達が遅れるので、「古い位置の情報」を受け取ることになり、見かけの速度は遅く見えます。

ここまでの直感的な説明を踏まえると、
「ジェットをできるだけ前方向に飛ばせば見かけ速度はどんどん大きくなるはずだ」と思いがちですが、実はそう単純ではありません。

その理由は、時間短縮効果と横方向の進みとのトレードオフにあります。
後でグラフで整理しますが、先に言葉でイメージを説明すると次の通りです。

• 角度を小さくすると、光が早く届くことで「時間を稼げる」効果は大きくなる一方、横方向の進みが小さくなる
• 角度を大きくすると、横方向の進みは大きい一方で、時間短縮効果は弱まってしまう

この2つの効果のバランスが取れた角度で、見かけ速度は最大になります。

見かけ速度を1次元で描画

数式だけではイメージしづらいので、まずは1次元のグラフで可視化してみます。
横軸に運動角度 $\theta$、縦軸に見かけの速度 $\beta_{\mathrm{app}}$ をとり、いくつかの速度 $\beta$（ここでは $\beta$ を 0.01 刻みでプロット）について描画します。

コード

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors as mcolors

# -----------------------------
# パラメータ設定
# -----------------------------
theta_vals = np.linspace(0.1, 179.9, 1000) * np.pi/180  # 角度 (ラジアン)
beta_list = np.arange(0, 1.01, 0.01)                   # β = 0 ~ 1.0

# -----------------------------
# カラーマップ設定
# -----------------------------
cmap = cm.turbo
norm = mcolors.Normalize(vmin=beta_list.min(), vmax=beta_list.max())

# -----------------------------
# プロット準備
# -----------------------------
fig, ax = plt.subplots(figsize=(10, 6))

for beta in beta_list:
    beta_app = (beta * np.sin(theta_vals)) / (1 - beta * np.cos(theta_vals))
    ax.plot(theta_vals*180/np.pi, beta_app, color=cmap(norm(beta)), linewidth=1)

# -----------------------------
# 軸・ラベル・タイトル
# -----------------------------
ax.set_xlabel(r"Angle, $\theta$ [degrees]")
ax.set_ylabel(r"Apparent velocity, $\beta_{\rm app}$")
ax.set_ylim(0, 8)
ax.set_xlim(0, 180)
ax.grid(True, linestyle='--', alpha=0.6)

# -----------------------------
# カラーバーを追加
# -----------------------------
sm = cm.ScalarMappable(cmap=cmap, norm=norm)
cbar = fig.colorbar(sm, ax=ax, label=r"Velocity, $\beta$")
cbar.set_ticks(np.linspace(0.1, 1.0, 10))

ax.set_title(r"Apparent velocity vs. angle for different $\beta$ values")

# ----------------------------------------
# 注釈とガイドライン
# ----------------------------------------
# θ=90° の縦線
ax.axvline(x=90, color='gray', linestyle='--', linewidth=1.5, alpha=0.7)

# Approaching / Receding の注釈
ax.text(80, 7.5, "Approaching", color='tab:blue',
        ha="right", va="top", rotation=0,
        fontweight="bold",
        bbox=dict(facecolor="white", edgecolor="none",
                  boxstyle="round,pad=0.6", alpha=0.7))

ax.text(100, 7.5, "Receding", color='tab:red',
        ha="left", va="top", rotation=0,
        fontweight="bold",
        bbox=dict(facecolor="white", edgecolor="none",
                  boxstyle="round,pad=0.6", alpha=0.7))
ax.set_xticks(np.arange(0, 181, 10))

plt.show()

見かけ速度 $\beta_{\mathrm{app}}$ と角度 $\theta$ の関係

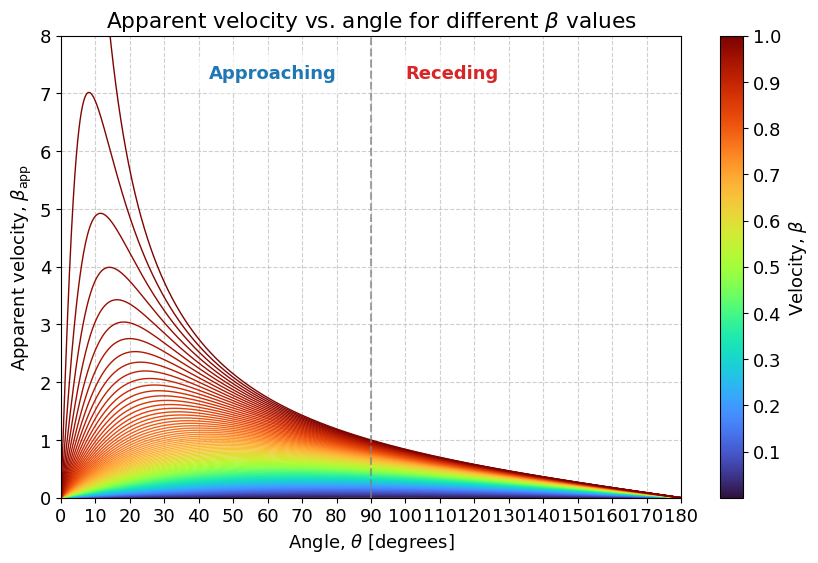
この図から、物体の速度 $\beta$ が大きくなると、見かけの速度 $\beta_{\mathrm{app}}$ が光速を超える（$\beta_{\mathrm{app}}>1$）ことがあるのがわかります。
また、興味深いことに $\beta$ が大きいほど、見かけ速度が最大になる角度 $\theta$ が前寄り（小さい値）にシフトしていくという点です。

見かけ速度を2次元で描画

1次元のプロットだけでも見かけ速度の特徴はよくわかりますが、筆者としてはパラメータ空間全体を俯瞰するのが好きなので、2次元ヒートマップでも描画してみます。

パラメータの配置は色々と好みによりますが、ここでは見かけ速度の変化が直感的にわかりやすいように、横軸に $\beta$、縦軸に運動角度 $\theta$ をとり、色で $\beta_{\mathrm{app}}$ を示すことにします。

コード

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors

# ----------------------------------------
# パラメータ定義
# ----------------------------------------
beta_vals = np.linspace(0.01, 0.99, 800)              # 真の速度 β
theta_vals = np.linspace(1, 179, 1600) * np.pi/180    # 観測角度 θ (ラジアン)
B, TH = np.meshgrid(beta_vals, theta_vals)

# 見かけ速度 β_app
v_app = (B * np.sin(TH)) / (1 - B * np.cos(TH))

# 等高線レベル
levels = [0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,2,3,4,5,6,7]

# ----------------------------------------
# プロット準備 (axスタイル)
# ----------------------------------------
fig, ax = plt.subplots(figsize=(10, 10))
cmap = plt.cm.turbo
norm = colors.PowerNorm(gamma=0.5, vmin=0, vmax=7)

# 背景グラデーション
mesh = ax.pcolormesh(
    B, TH*180/np.pi, v_app,
    cmap=cmap, shading='auto', norm=norm
)

# カラーバー
cbar = fig.colorbar(mesh, ax=ax, label=r"Apparent velocity, $\beta_{\rm app}$")
cbar.set_ticks(levels)
cbar.set_ticklabels([f"{t:.1f}" if t < 1 else f"{int(t)}" for t in levels])

# ----------------------------------------
# 等高線 (グレースケール)
# ----------------------------------------
cmap_gray = plt.cm.gray
contour_colors = [cmap_gray(norm(lv)) for lv in levels]

contours = ax.contour(
    B, TH*180/np.pi, v_app,
    levels=levels, colors=contour_colors, linewidths=0.8
)

positions = [(b, 90) for b in levels[1:10]]
ax.clabel(
    contours,
    levels=levels[:10],
    inline=True, fontsize="small",
    fmt=lambda x: rf"{x:.1f}$c$",
    colors=contour_colors[:10],
    manual=positions
)

ax.clabel(
    contours,
    levels=levels[10:],
    inline=True, fontsize="small",
    fmt=lambda x: rf"{int(x)}$c$",
    colors=contour_colors[10:],
)

# ----------------------------------------
# 注釈とガイドライン
# ----------------------------------------
ax.axhline(y=90, color='w', linestyle='--', linewidth=1.5, alpha=0.7)

ax.text(0.05, 80, "Approaching", color='tab:blue', rotation=90,
        ha="center", va="top", transform=ax.transData,
        fontweight="bold",
        bbox=dict(facecolor="white", edgecolor="none",
                  boxstyle="round,pad=0.6", alpha=0.7))

ax.text(0.05, 100, "Receding", color='tab:red', rotation=90,
        ha="center", va="bottom", transform=ax.transData,
        fontweight="bold",
        bbox=dict(facecolor="white", edgecolor="none",
                  boxstyle="round,pad=0.6", alpha=0.7))

# ----------------------------------------
# 軸・タイトル・グリッド
# ----------------------------------------
ax.set_xlabel(r"Velocity, $\beta$")
ax.set_ylabel(r"Angle, $\theta$ [deg]")
ax.set_xticks(np.arange(0.1, 1.0, 0.1))
ax.set_yticks(np.arange(10, 180, 10))
ax.grid(True, linestyle='--', linewidth=0.5, color='gray', alpha=0.6)
ax.set_title("Contour map of apparent velocity")

plt.show()

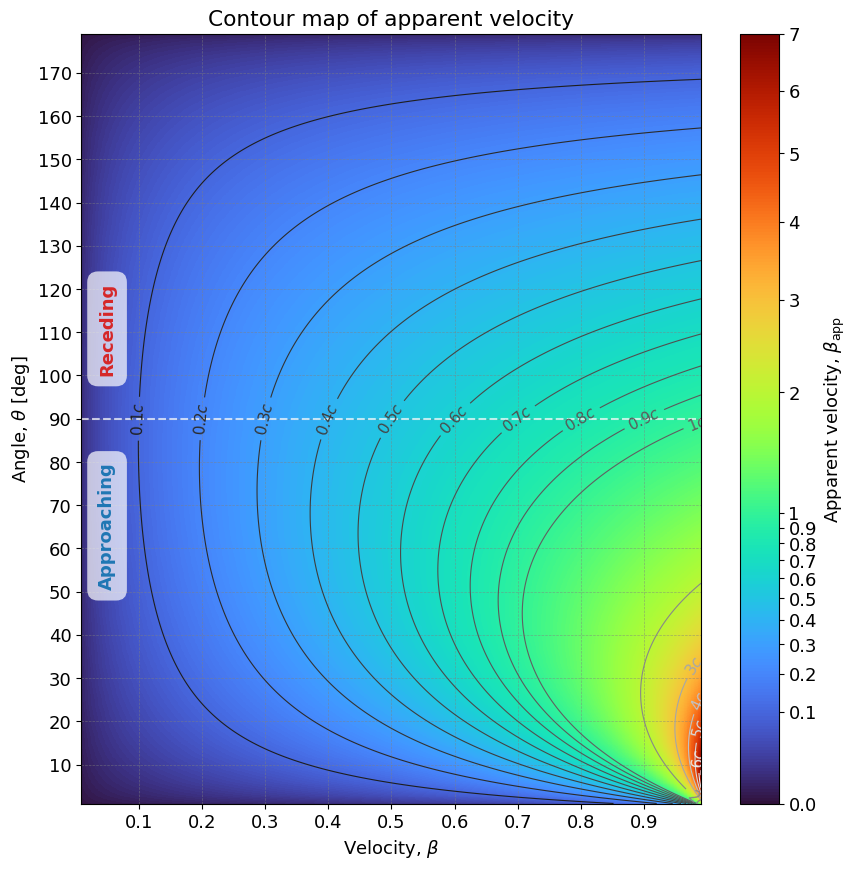
見かけ速度 $\beta_{\mathrm{app}}$ のヒートマップ

コード

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors

# ----------------------------------------
# パラメータ設定
# ----------------------------------------
beta_vals = np.linspace(0.01, 0.99, 800)              # 真の速度 β
theta_vals = np.linspace(1, 179, 1600) * np.pi/180    # 観測角度 θ (ラジアン)
B, TH = np.meshgrid(beta_vals, theta_vals)

# 見かけ速度 β_app の計算
v_app = (B * np.sin(TH)) / (1 - B * np.cos(TH))

# 等高線レベル
levels = [0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,2,3,4,5,6,7]

# ----------------------------------------
# プロット準備 (axスタイル)
# ----------------------------------------
fig, ax = plt.subplots(figsize=(10, 10))
ax.set_xscale("logit")  # βの両端を見やすくスケーリング
cmap = plt.cm.turbo

# 背景グラデーション
norm = colors.PowerNorm(gamma=0.5, vmin=0, vmax=7)
mesh = ax.pcolormesh(
    B, TH*180/np.pi, v_app,
    cmap=cmap, shading='auto', norm=norm
)

# カラーバー
cbar = fig.colorbar(mesh, ax=ax, label=r"Apparent velocity, $\beta_{\rm app}$")
cbar.set_ticks(levels)
cbar.set_ticklabels([f"{t:.1f}" if t < 1 else f"{int(t)}" for t in levels])

# ----------------------------------------
# 等高線
# ----------------------------------------
cmap_gray = plt.cm.gray
contour_colors = [cmap_gray(norm(lv)) for lv in levels]

contours = ax.contour(
    B, TH*180/np.pi, v_app,
    levels=levels, colors=contour_colors, linewidths=0.8
)

positions = [(b, 90) for b in levels[1:10]]
ax.clabel(
    contours,
    levels=levels[:10],
    inline=True, fontsize="small",
    fmt=lambda x: rf"{x:.1f}$c$",
    colors=contour_colors[:10],
    manual=positions
)

ax.clabel(
    contours,
    levels=levels[10:],
    inline=True, fontsize="small",
    fmt=lambda x: rf"{int(x)}$c$",
    colors=contour_colors[10:],
)

# ----------------------------------------
# 注釈とガイドライン
# ----------------------------------------
ax.axhline(y=90, color='w', linestyle='--', linewidth=1.5, alpha=0.7)

ax.text(0.05, 80, "Approaching", color='tab:blue', rotation=90,
        ha="center", va="top", transform=ax.transData,
        fontweight="bold",
        bbox=dict(facecolor="white", edgecolor="none",
                  boxstyle="round,pad=0.6", alpha=0.7))

ax.text(0.05, 100, "Receding", color='tab:red', rotation=90,
        ha="center", va="bottom", transform=ax.transData,
        fontweight="bold",
        bbox=dict(facecolor="white", edgecolor="none",
                  boxstyle="round,pad=0.6", alpha=0.7))

# ----------------------------------------
# 軸・タイトル・グリッド
# ----------------------------------------
ax.set_xlabel(r"Velocity, $\beta$")
ax.set_ylabel(r"Angle, $\theta$ [deg]")
ax.set_xticks([0.01, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.99])
ax.set_yticks(np.arange(10, 180, 10))
ax.grid(True, linestyle='--', linewidth=0.5, color='gray', alpha=0.6)
ax.set_title("Contour map of apparent velocity")

plt.show()

見かけ速度 $\beta_{\mathrm{app}}$ のヒートマップ（$\beta \approx 1$ 付近を見やすいスケーリングに変更）

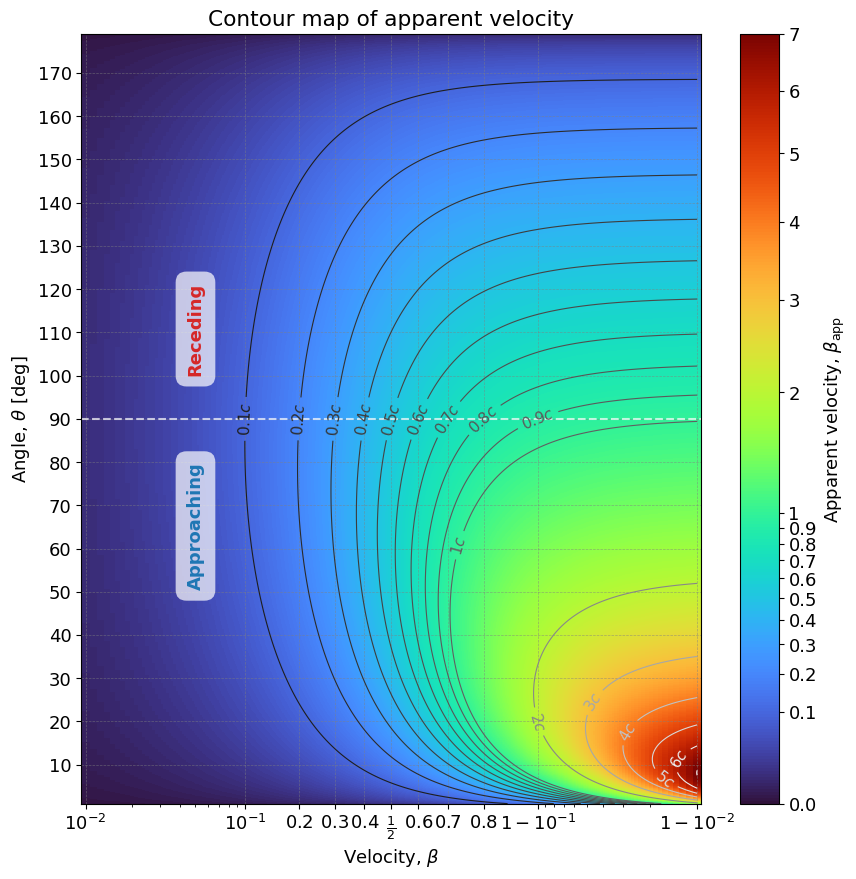
図から読み取れること

• 真横方向（$\theta = 90^\circ$）
  このとき $\beta_{\rm app} = \beta$ となり、見かけ速度は真の速度そのままです。
  横方向の運動は光行時間効果が効かないため、錯覚は生じません。

• 遠ざかる方向（receding jet, $\theta > 90^\circ$）
  常に $\beta_{\rm app} < \beta$ となります。
  光が余分に遅れて届くため、見かけの進みは鈍り、実速度より必ず遅く見えるのが特徴です。

• 近づく方向（approaching jet, $\theta < 90^\circ$）
  逆に $\beta_{\rm app} > \beta$ となります。
  光が短い間隔で届くことで進み具合が増幅され、場合によっては光速を超えて見えます。
  特に $\beta \gtrsim 0.7$ では、ある角度範囲で $\beta_{\rm app} > 1$（超光速運動） がはっきり現れます。
  この図では $\beta=0.99$ までを表示しており、見かけ速度の最大で $7c$ 程度に達していることがわかります。

補足

ここまでで、見かけ速度の基本式とその直感的な理解が得られました。
ここからは一歩踏み込んで、見かけ速度がどの角度で最大化されるのか、そしてそのときどれくらい速く見えるのかを解析的に求めていきます。

数式を解くだけでなく、グラフで可視化しながら「どの角度でピークになるのか？」を直感的に掴んでいきましょう。
さらに最後には、実際の天体 SS 433 を例に歳差運動を考慮した見かけ速度マップを描き、理論と観測がどのように結びつくのかを体感します。

ピーク速度の解析解

見かけ速度の式（*）を角度 $\theta$ で微分すると

\frac{d}{d\theta}\beta_{\rm app} 
= \frac{\beta \cos\theta - \beta^2}{(1 - \beta \cos\theta)^2}

となります。分子がゼロになる条件から

\cos\theta_{\arg \max} = \beta

を得ます。したがって、見かけ速度を最大化する角度は

\theta_{\arg \max} = \arccos \beta.

このときの最大見かけ速度は

\beta_{\rm app,max} = \frac{\beta}{\sqrt{1 - \beta^2}} = \beta \gamma

となります。

グラフで確認

この関係式をグラフで確認してみましょう。
横軸に $\beta$、左の縦軸に $\theta_{\arg \max}$、右の縦軸に $\beta_{\rm app,max}$ をとると、それぞれがどのように変化するかが一目で分かります。

コード

import numpy as np
import matplotlib.pyplot as plt

# βを0〜0.99までスキャン
beta_vals = np.linspace(0.01, 0.99, 500)

# θ_max = arccos(β)
theta_max = np.arccos(beta_vals)  # ラジアン
theta_max_deg = np.degrees(theta_max)

# β_app,max = β / sqrt(1-β^2)
beta_app_max = beta_vals / np.sqrt(1 - beta_vals**2)

# プロット
fig, ax1 = plt.subplots(figsize=(8, 5))

color1 = "tab:gray"
ax1.plot(beta_vals, theta_max_deg, color=color1, label=r"$\theta_{\arg \max}$")
ax1.set_xlabel(r"Velocity, $\beta$")
ax1.set_ylabel(r"Max angle, $\theta_{\arg \max}$ [deg]", color=color1)
ax1.tick_params(axis="y", labelcolor=color1)
ax1.set_xlim(0, 1)
ax1.set_ylim(0, 90)
ax1.grid(True, linestyle="--", alpha=0.6)
ax1.set_xticks(np.arange(0, 1.1, 0.1))
ax1.set_title(r"Maximum apparent velocity and corresponding angle vs. $\beta$")

# 第二軸で β_app,max を表示
ax2 = ax1.twinx()
color2 = "tab:purple"
ax2.plot(beta_vals, beta_app_max, color=color2, label=r"$\beta_{\rm app,max}$")
ax2.set_ylabel(r"Max apparent velocity, $\beta_{\rm app,max}$", color=color2)
ax2.tick_params(axis="y", labelcolor=color2)
ax2.set_ylim(0, 7)

plt.show()

最大見かけ速度とピーク角度の関係（$\beta$を横軸に表示）

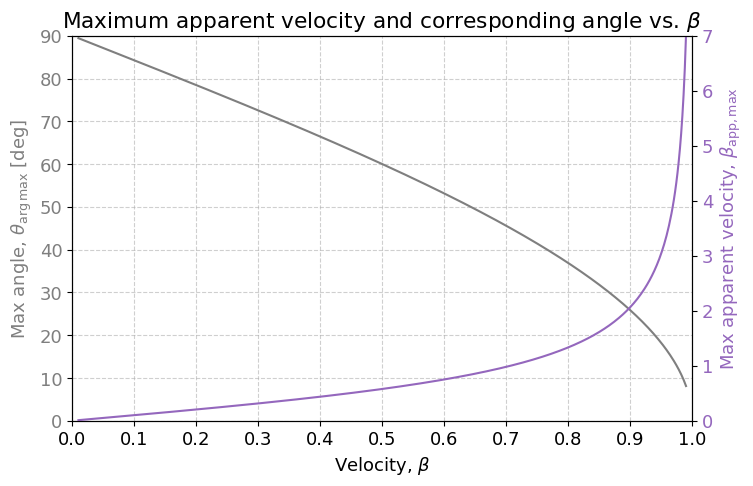
結果を見ると、$\beta$ が大きくなるにつれてピーク角度 $\theta_{\arg \max}$ がどんどん前寄りになり、同時に $\beta_{\rm app,max}$ が急激に大きくなることが分かります。
つまり、高速ジェットほど「より前を向いたとき」に見かけ速度が最大化されるのです。

先ほどの図は、2軸に整理することで関係性を見やすくしていましたが、まだ「物理的にどんな形をしているのか」という直感はつかみにくいかもしれません。

そこで次は、角度と速度を 2 次元平面 に並べて可視化し、各 $\beta$ に対応する見かけ速度が最大化するベクトルの先端をプロットしてみます。

コード

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors as mcolors
from mpl_toolkits.axes_grid1 import make_axes_locatable

# βのリスト
beta_list = np.linspace(0.01, 0.99, 400)

# カラーマップ（見かけ速度でカラーリング）
cmap = cm.turbo
# norm = mcolors.Norm(vmin=0, vmax=7)  # β_app の範囲で調整
norm = mcolors.Normalize(vmin=0, vmax=7)  # β_app の範囲で調整


# 図を準備
fig, ax = plt.subplots(figsize=(8, 8))

for beta in beta_list:
    theta = np.arccos(beta)  # cosθ = β の角度
    # ベクトルの先端
    x = beta * np.cos(theta)
    y = beta * np.sin(theta)
    # 見かけ速度 β_app
    beta_app = (beta * np.sin(theta)) / (1 - beta * np.cos(theta))
    ax.plot(x, y, '.', color=cmap(norm(beta_app)))

# 軸ラベルと装飾
ax.axhline(0, color='k', lw=0.8)
ax.axvline(0, color='k', lw=0.8)
ax.set_xlabel(r"$\beta_\parallel$ (line of sight, approaching)")
ax.set_ylabel(r"$\beta_\perp$ (plane of sky)")
ax.set_title(r"Locus at $\theta_{\arg \max}=\arccos \beta$, colored by $\beta_{\rm app,max}$")
ax.set_xticks(np.arange(0, 1.1, 0.1))
ax.set_yticks(np.arange(0, 1.1, 0.1))
ax.set_aspect("equal")
ax.set_xlim(-0.05, 1)
ax.set_ylim(-0.05, 1)
ax.grid(True, linestyle="--", alpha=0.6)

# x=0.5 の境界線
ax.axvline(x=0.5, color="gray", linestyle="--", linewidth=1.5, alpha=0.7)
ax.text(
    0.5, 0.85, "Superluminal threshold", 
    ha="center", va="center", color="gray", fontweight="bold"
)

# カラーバー
sm = cm.ScalarMappable(cmap=cmap, norm=norm)
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.05)
cbar = fig.colorbar(sm, cax=cax, label=r"Max apparent velocity, $\beta_{\rm app,max}$")

plt.show()

最大見かけ速度を与える点の軌跡（$\beta_\parallel$–$\beta_\perp$ 平面）

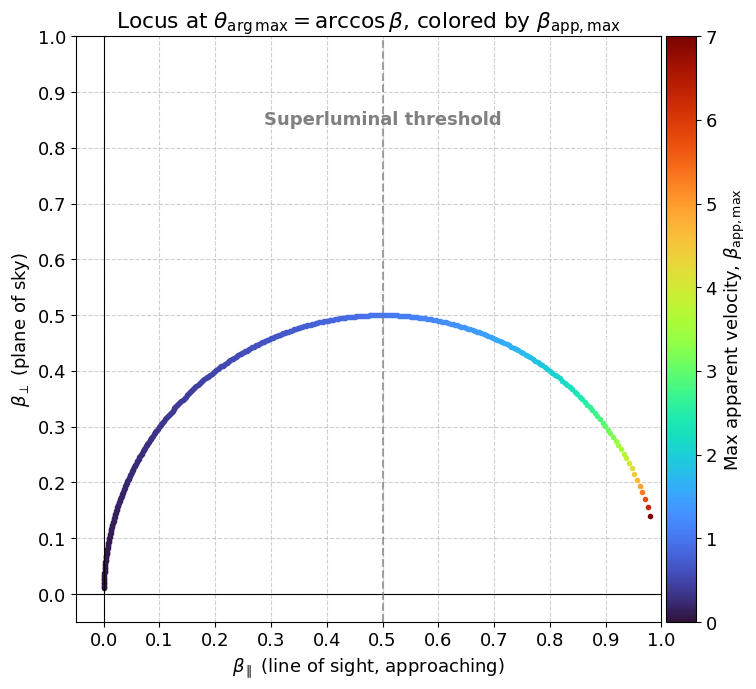
このように 円弧を描くような美しい軌跡 が現れる様子がわかります。

図から読み取れること

• 超光速に見えるタイミング
  初めて $\beta_{\rm app} \ge 1$ となるのは、$\beta_\parallel = \beta_\perp = 0.5$ となるときです
  （i.e., $\beta = \frac{1}{\sqrt{2}},\ \theta = 45^\circ$）。
  前方向と横方向への進みがちょうど釣り合う角度で、このときから見かけ速度が光速を超えるというのは、幾何学的に美しいですね。
• トレードオフの関係
  物体の速度が遅い場合は、視線垂直方向（横方向）の運動が見かけ速度を大きくします。
  しかし速度が十分に大きくなると、光行時間効果の寄与が優勢となり、前寄りの角度のほうがより見かけ速度が大きく見えるようになります。

次節では、この円弧のように見える対称曲線を数式で表してみます。

最大見かけ速度を与える点の軌跡

見かけ速度が最大になる条件は

\cos\theta_{\mathrm{\arg \max}} = \beta

でした。ここで

\beta_\parallel = \beta \cos\theta, \qquad
\beta_\perp = \beta \sin\theta

とおくと、

\beta_\parallel = \beta^2, \qquad
\beta_\perp = \beta \sqrt{1 - \beta^2}

となります。さらに $\beta^2 = \beta_\parallel$ を代入すると

\beta_\perp = \sqrt{\beta_\parallel (1 - \beta_\parallel)}

が得られます。これを平方完成すると

\beta_\perp = \sqrt{\frac{1}{4} - \left(\beta_\parallel - \frac{1}{2}\right)^2}

となり、両辺を二乗すると

\left(\beta_\parallel - \frac{1}{2}\right)^2 + \beta_\perp^2 = \left(\frac{1}{2}\right)^2

が得られます。これはまさに 中心 $(\beta_\parallel, \beta_\perp)=\left(\frac{1}{2}, 0\right)$、半径 $r=\frac{1}{2}$ の円の方程式を表しています。
さらに $\beta_\perp \ge 0$ なので、この式が表すのは円の上半分（上半円）に相当します。

言い換えると、速度成分がちょうど $\beta_\parallel=0.5$を軸にして美しくバランスしている 様子を見ていることになります。

次節では、この半円上の特別な点として $\beta_\parallel=\beta_\perp=0.5$（$\theta=45^\circ$）が現れることを確認し、見かけ速度が光速を超える瞬間を幾何学的に再解釈していきます。

見かけの速度が光速を超える条件

見かけの速度が光速を超える条件について整理します。

式 $\beta_{\rm app} > 1$ が満たすのは、

\frac{\beta \sin\theta}{1 - \beta \cos\theta} > 1

のときであり、これを変形すると、

\begin{align}
\beta(\sin\theta + \cos\theta) &> 1\\[6pt]
\beta \sqrt{2}\,\sin\!\left(\theta + \tfrac{\pi}{4}\right) &> 1
\end{align}

が得られます。ここで $\sin(\cdot)$ が最大値 1 をとるのは $\theta=\pi/4$ のときなので、見かけ速度が初めて光速を超える条件は

\beta > \frac{1}{\sqrt{2}} \approx 0.707

となります。

実際に図にしてみるとよく分かります。$\beta=1/\sqrt{2}$、$\theta=45^\circ$ の場合、単位時間$\Delta t$の間にそれぞれ $d_\parallel = d_\perp = 0.5c\Delta t$ 進むことになります。つまり、$0.5c\Delta t$ 近づくことで $0.5c\Delta t$ だけ観測時間を稼ぐことができ、その結果横方向へ倍に見かけ上進むことができるわけです。このように、数式と幾何学がきれいに対応しているのがわかります。

SS 433の歳差運動に伴う見かけ速度の変化

SS 433 はおよそ $0.26c$ の速度で噴出するジェットを持ち、歳差運動する天体です。
ジェットの基本的な性質については、以前の記事

で解説していますので、あわせてご覧ください。

ここでは、歳差運動の幾何学を定式化し、それに基づいて見かけ速度が位相とともにどのように変化するかを解析していきます。

歳差運動するジェットの歳差位相 $\psi$ における視線角度は

\theta(\psi)
= \arccos\!\Bigl[
  \cos i \cos\theta_{\rm open}
  + \sin i \sin\theta_{\rm open} \cos(2\pi\psi)
\Bigr].

で与えられます。

ここで登場するパラメータは次の通りです：

• $i$：系の傾斜角（軌道面と視線のなす角）。SS 433では $i \approx 79^\circ$。
• $\theta_{\rm open}$：歳差円錐の半開角。SS 433では $\theta_{\rm open} \approx 20^\circ$。
• $\psi$：歳差位相（0〜1で1周期を表現）。

この式で得られる $\theta(\psi)$ が、ある位相でのジェットの視線方向角です。

• 接近ジェット（approaching jet） の角度は

  \theta_{\rm approach} = \theta(\psi)
  

• 後退ジェット（receding jet） の角度は

  \theta_{\rm recede} = \pi - \theta(\psi)
  

  となります（対称的な歳差運動を仮定）。
  （※本来は後退ジェットは $\pi+\theta$ ですが、角度を $0 \le \theta \le \pi$ の範囲で定義することで見かけ速度の計算時に分子が負になるのを避けています。物理的な扱いは同じです。）

各位相における見かけ速度は、式（*）にそれぞれのジェットの角度$\theta_{\mathrm{approach}}, \theta_{\mathrm{recede}}$ と、速度 $\beta = 0.26$ を代入することで計算します。

コード

import numpy as np
import matplotlib.pyplot as plt

# -----------------------------
# パラメータ設定 (SS 433)
# -----------------------------
beta = 0.26
i = np.deg2rad(79.0)
theta_open = np.deg2rad(20.0)
psi_vals = np.linspace(0, 1, 500)  # フル位相 0〜1

# -----------------------------
# 視線角度の計算
# -----------------------------
cos_theta = np.cos(i) * np.cos(theta_open) + np.sin(i) * np.sin(theta_open) * np.cos(2*np.pi*psi_vals)
angle_approach = np.degrees(np.arccos(np.clip(cos_theta, -1.0, 1.0)))  # Approaching jet の視線角
angle_recede   = 180 - angle_approach                                 # Receding jet の視線角

# -----------------------------
# 見かけの速度
# -----------------------------
angle_approach_rad = np.radians(angle_approach)
angle_recede_rad   = np.radians(angle_recede)

beta_app_approach = (beta * np.sin(angle_approach_rad)) / (1 - beta * np.cos(angle_approach_rad))
beta_app_recede   = (beta * np.sin(angle_recede_rad))   / (1 - beta * np.cos(angle_recede_rad))

# -----------------------------
# プロット
# -----------------------------
fig, (ax1, ax2) = plt.subplots(
    2, 1, figsize=(10, 8), sharex=True, gridspec_kw={'hspace': 0.0}
)

# --- 上段：視線角度 vs 歳差位相 ---
ax1.plot(psi_vals, angle_approach, color="tab:blue", label="Approaching jet")
ax1.plot(psi_vals, angle_recede,  color="tab:red",  label="Receding jet")
ax1.grid(True, linestyle="--", alpha=0.6)
ax1.set_ylabel(r"Angle, $\theta$ [deg]")
ax1.legend()
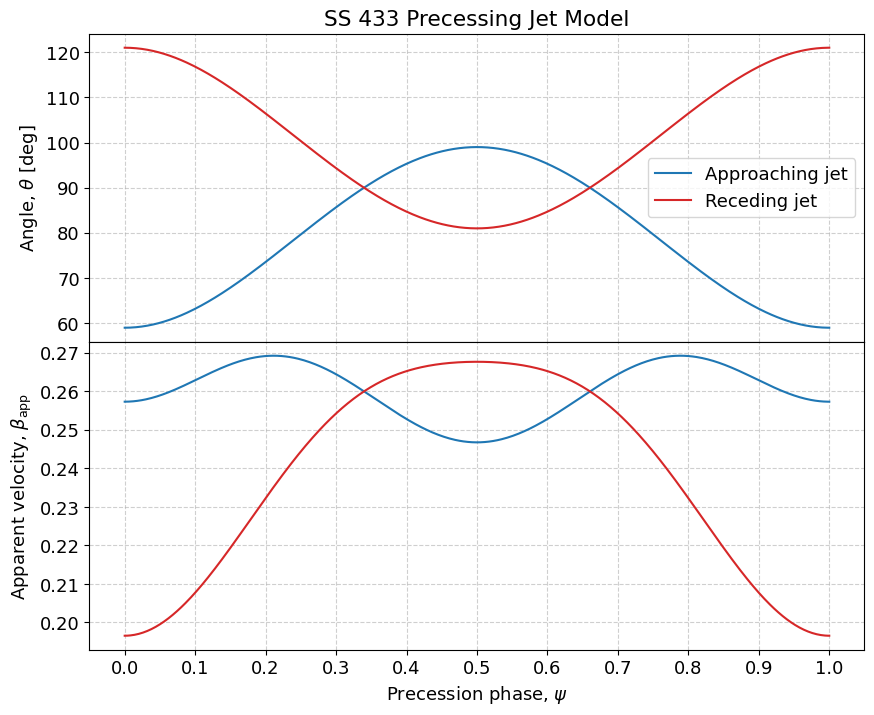
ax1.set_title("SS 433 Precessing Jet Model")

# --- 下段：見かけ速度 vs 歳差位相 ---
ax2.plot(psi_vals, beta_app_approach, color="tab:blue")
ax2.plot(psi_vals, beta_app_recede,  color="tab:red")
ax2.set_xlabel(r"Precession phase, $\psi$")
ax2.set_ylabel(r"Apparent velocity, $\beta_{\rm app}$")
ax2.grid(True, linestyle="--", alpha=0.6)
ax2.set_xticks(np.arange(0, 1.1, 0.1))

plt.show()

SS 433 における歳差位相と見かけ速度の関係

図の見方

• 面白いことに、ジェットの視線角度 $\theta$ が最もこちらを向く（最小）タイミングでは、見かけ速度は最大になりません。
  実際には $\theta \approx 75^\circ$ 付近でピークとなるのが興味深い点です。

• また、最大見かけ速度は約 $0.27c$ となり、真のジェット速度 $0.26c$ を上回ります。
  このことからも、見かけ速度だけを根拠に「ジェットがより速い」と結論づけるのは危険であり、実速度の推定には歳差角や光行時間補正などの幾何学的要素を正しく考慮する必要があることがわかります。

最後に、研究現場での活用事例を簡単に紹介させてください。
SS 433 の文脈では、このような光行差を考慮した解析は、VLBA 電波観測でのブロブ速度推定（Jeffrey et al. 2016）や、
手前味噌ですが筆者らの Chandra X線観測データと歳差ジェットモデルとの比較解析（Sakai et al. 2025）でも行われています。

興味のある方はぜひご覧ください。また、質問やコメントなども歓迎ですので、ぜひ気軽にフィードバックいただければ嬉しいです。

より観測現場に即した応用方法については、こちらの記事もぜひご参照ください：

おわりに

本記事では、

• 光行時間効果から導かれる見かけ速度の数式
• 角度依存の直感的な理解と、光速を超える条件
• SS 433 を例にした具体的な見かけ速度マッピング

を通じて、「なぜジェットが光速を超えて見えるのか」を整理しました。

見かけ速度は、一見トリックのように思えますが、少しずつイメージを膨らませると自然に理解できる現象です。
前方向と横方向の運動のバランスが見かけ速度を決めているという点は、非常に興味深いところです。

どんなに遅いジェットでもこの効果は必ず含まれますが、ジェット速度が光速の数十％以上のケースでは、光行時間を無視すると推定を誤る可能性があります。
だからこそ、研究の現場では標準的な解析ステップとしてこの補正が取り入れられています。

そして最後に、一見すると「前に進むと速く見える」というのは直感に合わないかもしれません。
しかし、式 (*) を ($\beta \ll 1$) の極限で展開すると

\beta_{\rm app} \approx \beta \sin\theta + \beta^2 \sin\theta \cos\theta + \cdots

となり、一次の項 ($\beta \sin\theta$) は古典的に考える見かけ速度の感覚と一致します。
つまり、相対論的な式も低速の世界では、きちんと私たちの直感に戻るのです。

この記事が、超光速運動（superluminal motion）を初めて学ぶ方にとって、直感を深める一助になれば嬉しいです。