【機械学習モデリング記録】002重回帰

はじめに

yukineです．
不定期更新のモデリング記録第2回です．
今回は重回帰を扱います．

前回↓
https://qiita.com/yukine_kamihata/items/efb1510acbae3d094588

数式の理解

目的変数を$y$，説明変数を$X$，係数を$\beta$，誤差を$\varepsilon$として，行列表示すると

\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \varepsilon

目的は残差平方和を最小化することです．

\displaylines{
L(\boldsymbol{\beta}) = \|\mathbf{y} - \mathbf{X}\boldsymbol{\beta}\|^2
= (\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^\mathsf{T} (\mathbf{y} - \mathbf{X}\boldsymbol{\beta}) \\

L(\boldsymbol{\beta}) = -2\mathbf{X}^\mathsf{T}\mathbf{y} + 2\mathbf{X}^\mathsf{T}\mathbf{X} + \boldsymbol{\beta}^\mathsf{T}\mathbf{X}^\mathsf{T}\mathbf{X}\boldsymbol{\beta} \\

\frac{\partial L}{\partial \boldsymbol{\beta}} = -2\mathbf{X}^\mathsf{T}\mathbf{y} + 2\mathbf{X}^\mathsf{T}\mathbf{X}\boldsymbol{\beta} = 0 \\

\boldsymbol{\beta} = (\mathbf{X}^\mathsf{T}\mathbf{X})^{-1}\mathbf{X}^\mathsf{T}\mathbf{y}

} 

実装

まずはnumpyで実装してみます．

numpy

import numpy as np

class MultipleLinearRegression:
  def __init__(self):
    self.beta = None

  # 学習
  def fit(self, X, y):
    """
    X: (n_samples, n_features)
    y: (n_samples,)
    """

    n_samples = X.shape[0]

    # バイアス項を追加
    X_bias = np.colum_stack((np.ones(n_samples), X))

    self.beta = np.linalg.inv(X_bias.T @ X_bias) @ (X_bias.T @ y)

  # 予測
  def predict(self, X):

    n_samples = X.shape[0]

    # バイアス項を追加
    X_bias = np.column_stack((np.ones(n_samples), X))
    
    return X @ self.beta

同様に，scikit-learnで次のように記述できます．

sklearn

import numpy as np
from sklearn.linear_model import LinearRegression

# モデル作成
model = LinearRegression()

# 学習
model.fit(X_train, y_train)

# 予測
y_test = model.predict(X_test)

実践: kaggleの住宅価格予測

前回同様，実際にkaggleの「House Prices - Advanced Regression Techniques」で試してみます。

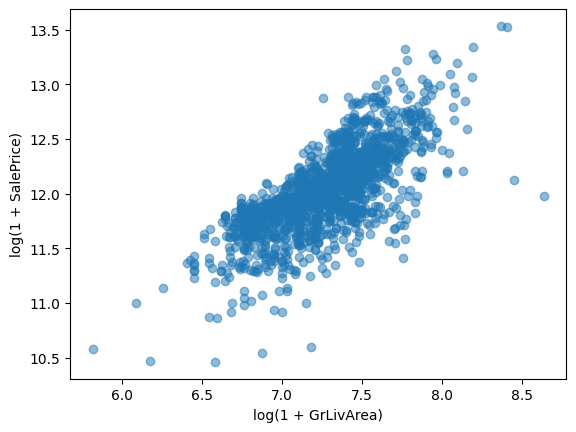
GrLivAreaとの相関を分析

plt.scatter(
      np.log1p(train_df['GrLivArea']), # 地上の居住面積を対数変換
      np.log1p(train_df['SalePrice']), # 価格を対数変換
      alpha=0.5
)

plt.xlabel("log(1 + GrLivArea)")
plt.ylabel("log(1 + SalePrice)")
plt.show()

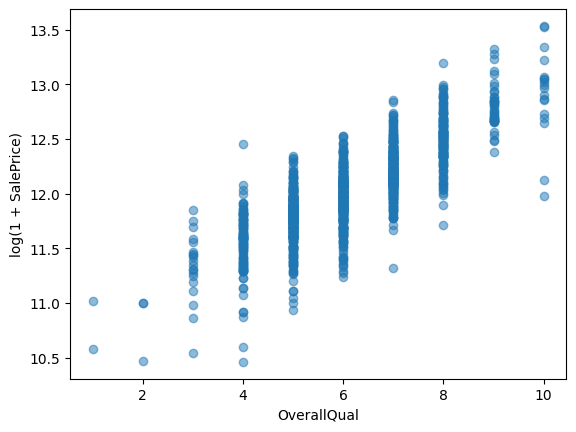
OverallQualとの相関を分析

plt.scatter(
      train_df['OverallQual'], # 住居の品質
      np.log1p(train_df['SalePrice']),
      alpha=0.5
)

plt.xlabel("OverallQual")
plt.ylabel("log(1 + SalePrice)")
plt.show()

まずはこの2つの特徴量を組み合わせて学習してみます．

学習

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression

X_train = train_df[['GrLivArea', 'OverallQual']]
y_train = train_df['SalePrice']

# 対数変換
X_train_log = X_train.copy()
X_train_log['GrLivArea'] = np.log1p(X_train_log['GrLivArea'])
y_train_log = np.log1p(y_train)

# 学習
model = LinearRegression()
model.fit(X_train_log, y_train_log)

予測

X_test = test_df[['GrLivArea', 'OverallQual']]

# 対数変換
X_test_log = X_test.copy()
X_test_log['GrLivArea'] = np.log1p(X_test_log['GrLivArea'])

# 予測
y_pred = np.expm1(model.predict(X_test_log))

submission = pd.DataFrame({"Id": test_df["Id"], "SalePrice": y_pred})
submission.to_csv("submission2025093003.csv", index=False)

RMSLEで0.20を下回りました．
次に説明変数を増やしてみます．

OverallQual, GrLivArea, TotalBsmtSF, GarageCars, YearBuilt

あたりを使ってみます．

features = ["OverallQual", "GrLivArea", "TotalBsmtSF", "GarageCars", "YearBuilt"]

X_train = train_df[features].fillna(0) # 欠損値を0で埋める．
y_train = train_df['SalePrice']

# 対数変換
X_train_log = X_train.copy()
X_train_log['GrLivArea'] = np.log1p(X_train_log['GrLivArea'])
y_train_log = np.log1p(y_train)

# 学習
model = LinearRegression()
model.fit(X_train_log, y_train_log)

X_test = test_df[features].fillna(0)

# 対数変換
X_test_log = X_test.copy()
X_test_log['GrLivArea'] = np.log1p(X_test_log['GrLivArea'])

# 予測
y_pred = np.expm1(model.predict(X_test_log))

submission = pd.DataFrame({"Id": test_df["Id"], "SalePrice": y_pred})
submission.to_csv("submission.csv", index=False)

5つの特徴量を使ったことで精度も改善されました．