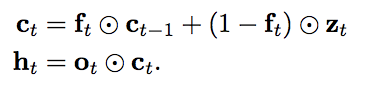はじめに
以前,KerasやTensorFlowを用いたRNN(LSTM)による時系列データ予測の導入記事を書いたのですが,予測対象が単純なsin波だったため,リカレントなネットワークの効果を実感できずに終わってしまっていました.また,その記事を書いた後あたりにCNNを活用して計算処理の並列化を進め,LSTMよりも高速な学習を行うQRNNが発表されたため,今回はもう少し複雑な時系列情報に対してQRNNの効果を試しつつ,CNNやRNNとの効果の違いをみてみます.
なお,備忘録としてざっくりとしたQRNNの解説を載せていますが,より詳しく,わかりやすい以下のような解説が多数あげられていますので,詳細等が気になる方はそちらをご覧ください.
参考文献
- QRNNでLSTM(深層学習を用いた時系列分析)をスピードアップ(次世代システム研究室様)
- Quasi-Recurrent Neural Networks(ご注文は機械学習ですか?様)
QRNN(Quasi-Recurrent-Neural-Network)とは
2016年11月にSales Force研究所のJames Bradburyらによって発表された学習手法です.
単語の連続で表現される文章や,波形の連続である音声等,時間軸方向に情報を持つデータを学習させる際には,過去から未来に向けて計算結果を順々に伝播させていく手法がよいとされています.
RNNの一手法であるLSTMでは,ネットワークを構成する隠れ層によって,過去の出力値と媒介変数から現在の出力,媒介変数を算出し,それを伝播させていくという手法をとっていました.
しかし,この方法では,現在の出力を得るために過去の出力値と媒介変数の値の両方が必要になるため,並列計算ができず計算に時間がかかるという問題点がありました.
そこでQRNNでは,CNNの並列計算能力を部分的に活用し,時系列データ学習高速化を行なっています.QRNNの論文はこちらで読むことができ,chainerやtensorflowを用いた実装もgithubにて公開されています.今回はこちらのKerasによる実装コードを用いることとします.
論文内に記載されている,LSTM, CNN, QRNNのモデルの違いがわかりやすいのでこちらに引用しておきます.
こちらを見ると,QRNNのモデルのキーはConv層とfo-Pooling層であることが見て取れます.
Conv層
Conv層では隠れ層に入力する変数(z:入力,f:忘却率,o:出力率)を計算します.
Z = tanh(W_z * X)\\
F = \sigma(W_f * X)\\
O = \sigma(W_o * X)
LSTMと異なり,z, f, oは一つ前の時間の隠れ層の出力に依存していないため,この部分は並列計算が可能になります.Xは入力,Wはそれぞれに対する重みです.
X \in R^{T \times n}\\
Z \in R^{T \times m}\\
W_z, W_f, W_o \in R^{k \times n \times m}
nは入力Xの次元数,mはz,f,o の次元数です.
隠れ層
Conv層で算出したz_t, f_t, o_t(t-1の状態に非依存)と一つ前の時間の隠れ層の媒介変数c_(t-1)を用いて,現在の時間の隠れ層の媒介変数c_tと出力h_tを求めます.
LSTMと異なり,QRNNではc_(t-1)のみに依存し,h_(t-1)の影響を受けないので,時系列順にそった計算量が減少し,高速化が可能になっています.
論文には何種類かのc_t, h_t算出方法がのっていますが,今回は上記のfo-poolingを採用しました.
カオス時系列データ予測
実際にトイデータを用いて,QRNNの性能を見てみます.
先述した通りコードは〜を用いています.
ただし本コード,RNNのステップ関数部分の記述が上式と比べてみてあれ?と思ったところがあり,修正して利用しました.
def step(self, inputs, states):
prev_output = states[0]
z = inputs[:, :self.units]
f = inputs[:, self.units:2 * self.units]
o = inputs[:, 2 * self.units:]
z = self.activation(z)
f = f if self.dropout is not None and 0. < self.dropout < 1. else K.sigmoid(f)
o = K.sigmoid(o)
c = f * prev_output + (1 - f) * z # もとはoutput = f * prev_output + (1 - f) * z
output = o * c
return output, [ct] # もとは return output, [output]
修正後実際に精度が上がったのは確認しているのですが,こちらの理解不足の可能性も十分あります...
def create_qrnn_model(l_seq):
input_layer = Input(shape=(l_seq, 1))
qrnn_output_layer = QRNN(64, window_size=60, dropout=0)(input_layer)
prediction_result = Dense(1)(qrnn_output_layer)
model = Model(input=input_layer, output=prediction_result)
model.compile(loss="mean_squared_error", optimizer="adam")
return model
またざっくりとした比較のため,LSTM,CNNのモデルも作成し,学習を回しました.
def create_rnn_model(l_seq):
inputs = Input(shape=(l_seq, 1,))
x = LSTM(hidden_neurons, return_sequences=False)(inputs)
predictions = Dense(1, activation='linear')(x)
model = Model(input=inputs, output=predictions)
model.compile(loss="mean_squared_error", optimizer="rmsprop")
return model
def create_cnn_model(l_seq):
inputs = Input(shape=(l_seq, 1))
x = Conv1D(32, 3, activation='relu', padding='valid')(inputs)
x = Conv1D(32, 3, activation='relu', padding='valid')(x)
x = MaxPooling1D(pool_size=2)(x)
x = Conv1D(64, 3, activation='relu', padding='valid')(inputs)
x = Conv1D(64, 3, activation='relu', padding='valid')(x)
x = MaxPooling1D(pool_size=2)(x)
x = Flatten()(x)
x = Dense(128, activation='relu')(x)
x = Dense(64, activation='relu')(x)
predictions = Dense(1, activation='linear')(x)
model = Model(input=inputs, output=predictions)
model.compile(loss="mean_squared_error", optimizer="adam")
return model
また,今回学習させる時系列データとしてカオス時系列データを採用しました.
初期条件・境界条件を定めると以後の運動が決まるような簡単な系であっても,初期条件のわずかな差で大きく違った結果を生じ非常にランダムな振る舞いをする非線形力学系をカオスと呼びます.
カオスについての解説は省きますが,今回はその中でもDuffing振動子の系を用いました.
これは剛性のある振り子に減衰項と磁石による強制振動項を追加した系で,基礎方程式は
m\frac{d^2x}{dt^2}=−γ\frac{dx}{dt}+2ax−4bx^3+F_0cos(ωt+δ)
です.グラフにすると以下のようになります.
こちらについてはPythonでカオス・フラクタルを見よう!(jabberwocky0139様)のコードを使わせていただきました.
def duffing(var, t, gamma, a, b, F0, omega, delta):
"""
var = [x, p]
dx/dt = p
dp/dt = -gamma*p + 2*a*x - 4*b*x**3 + F0*cos(omega*t + delta)
"""
x_dot = var[1]
p_dot = -gamma * var[1] + 2 * a * var[0] - 4 * b * var[0]**3 + F0 * np.cos(omega * t + delta)
return np.array([x_dot, p_dot])
def create_duffing():
F0, gamma, omega, delta = 10, 0.1, np.pi / 3, 1.5 * np.pi
a, b = 1 / 4, 1 / 2
var, var_lin = [[0, 1]] * 2
# timescale
t = np.arange(0, 20000, 2 * np.pi / omega)
t_lin = np.linspace(0, 1000, 10000)
# solve
var = odeint(duffing, var, t, args=(gamma, a, b, F0, omega, delta))
var_lin = odeint(duffing, var_lin, t_lin, args=(gamma, a, b, F0, omega, delta))
x_lin, p_lin = var_lin.T[0], var_lin.T[1]
return x_lin, t_lin, p_lin
上式によって10000ステップのデータを作成し,それを150区間でランダムに分割し,訓練データ,テストデータを作成します.
craete_duffing()により作成した時系列データから,訓練,テストデータを生成する方法については深層学習ライブラリKerasでRNNを使ってsin波予測をご参照ください.
これにより,150ステップ分の入力Xがあった際の出力yが151ステップ目になる様なデータセットを作ります.
結果
学習データとモデルの作成が終わったので,実際に学習を行います.
学習後,時系列データのどこかをモデルへの入力長分(150)切り取り,
それを用いてその窓の次の出力を得ます.
得られた値を用いて入力窓を一つ分ずらし,さらに次の出力を得る...ということを繰り返すことで,
予測をどんどん先に伸ばしていきます(もちろん,予測長が伸びるにつれ精度は低下します).
コードで書くと以下のようになります.
def sequential_predict(self, dataf, l_seq, start=0):
now = dataf.iloc[start:start + l_seq].as_matrix()
df = pd.DataFrame(dataf.iloc[start + l_seq - 150: start + l_seq + 350].as_matrix())
df.columns = ["true_value(observed_value)"]
pred = []
for i in range(350):
p = self.model.predict(np.array([now]))
pred.append(p[0][0])
now = np.roll(now, -1)
now[-1] = pred[-1]
df["predict"] = [None] * 150 + pred
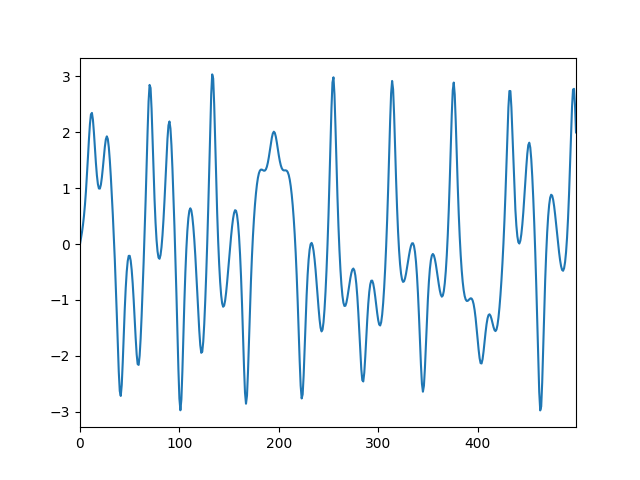
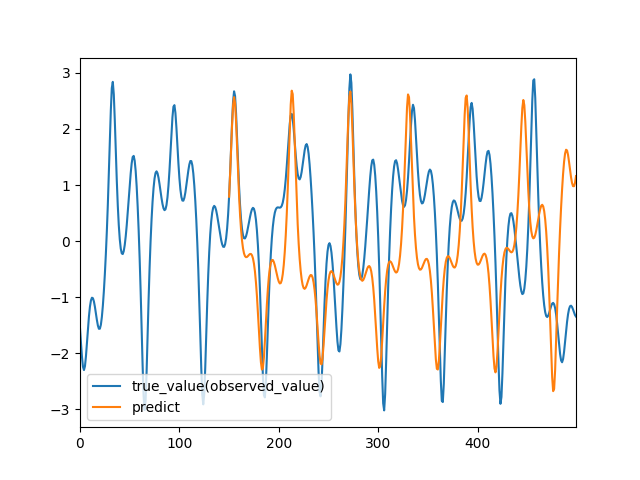
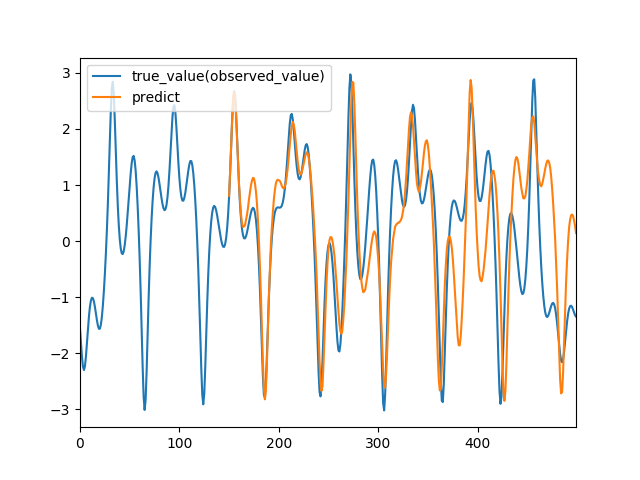
以下に,RNN, CNN, QRNNで予測をした結果を載せます.
RNN
CNN
QRNN
もちろん,最適化できていないため一概な比較はできませんが,QRNNが高い精度で予測できていることが見てとれるかと思います.
おわりに
QRNNを用いると短い学習時間で隠れ層をもつリカレントなモデルを構築することができます,時間ができたら為替データ等複雑なデータでも試してみたいです.
今回QRNNのzoneoutやpaddingの話は省略してしまっているので,時間ができれば追記したいと思います.