はじめに
これまで2回(前々回、前回)にわたって、テリー・ルドルフ教授のQ is for Quantumという本をベースに量子コンピューターについて説明しました。あんまりLGTMは付いてませんが、Facebook方面では多少ウケているようなので第3回を書いてみます。
前々回の記事では量子のもつれ(エンタングルメント)について、アインシュタイン大先生がある思考実験を披露し「これは光の速さを越えて情報が伝わることになるのでパラドックスだ。量子論はまだ不十分な理論であり、“隠れた変数”が存在するに違いない」と主張した、と説明しました。この主張は、1964年に理論的に、1982年に実験的に否定されたのですが、今回はこのことについて説明しようと思います。
EPRパラドックス
アインシュタイン大先生が披露したパラドックスは、1935年の論文の著者達の頭文字を取って「EPRパラドックス」と呼ばれます。EはEinsteinのEですね。まずは、これについて前々回での説明を再掲しておきます。
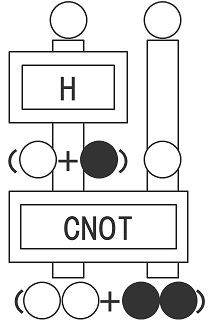
下の図のように、アダマールとCNOTを重ねて、2つの白を同時に入れると、下から白白と黒黒が混じり合った状態(白白+黒黒)の2つのボールが出てきます。その左右のボールをそれぞれ保管箱に入れ、左の箱を東京に運び、右の箱をニューヨークに運びます。そうすると、東京の箱を開けて観測して白か黒かが決まる瞬間に、同時にニューヨークの箱の中身も同じ色に決まるのです。これは光の速度を越えて情報が伝わることになるからパラドックスだ、というのがアインシュタイン大先生の指摘です。
Bellの不等式
これに対して、CERNの物理学者ジョン・スチュワート・ベル博士が1964年に「EPRパラドックスについて」という論文を出しました。
ここでベル先生が示したのは「Bellの不等式」と呼ばれ、アインシュタイン大先生の思考実験を利用して、ある測定した時に「もし“隠れた変数”が存在するならばその値は最大2にしかならない」1というものでした。Bellの不等式そのものは、「白黒のボールだけでなんとなく分かる」ようには説明できないので、この記事の最後に付録としておきます。
さてその後、光子などを使った実験が何度も試みられ、ついに1982年にフランスの物理学者アラン・アスペ博士の実験によって2より大きくなることが確認され、“隠れた変数”の存在が否定された、というわけです。
CHSHゲーム
Bellの不等式には色々なバージョンがあって、1982年にアスペ先生が行ったのは、Bell-CHSH不等式を使った「CHSHゲーム」というゲームの勝率を測定するものです。ゲームのルールは以下です。
- ゲームのプレイヤーはアリスとボブであり、2人で協力してゲームでの勝利に挑む。
- 2人は事前に戦略をよく相談した上で、東京とニューヨークに分かれる。ゲームの最中に相手との通信を行ってはいけない。
- 東京とニューヨークには一人ずつ審判がいる。審判はコインを投げて、その結果、裏か表かをプレイヤーに伝える。
- それに対してアリスとボブは白か黒かを選択する。
- コインのどちらか、あるいは両方が表の時、アリスとボブが同じ色を言ったなら勝ち。2枚のコインの両方とも裏の時だけは、アリスとボブが違う色を言ったなら勝ち。それ以外では負け。
- これを100回やった時、アリスとボブは平均して何回勝てるのか。
| 白白 | 白黒 | 黒白 | 黒黒 | |
|---|---|---|---|---|
| 表表 | 勝ち | 負け | 負け | 勝ち |
| 裏表 | 勝ち | 負け | 負け | 勝ち |
| 表裏 | 勝ち | 負け | 負け | 勝ち |
| 裏裏 | 負け | 勝ち | 勝ち | 負け |
アリスもボブも白と言い続ければ、コインが両方とも裏で無ければ勝てるので、勝率は75%です。これ以上の戦略があるでしょうか。実は、このゲームの勝率の上限は、Bell-CHSHの不等式を使うと75%になります。つまり“隠れた変数”が存在するならば、2人で白と言い続ける戦略より良い方法はありません。
しかし、量子のもつれを使うと$(2+\sqrt 2)\div 2=0.85355\dots$、85%以上勝てる戦略があり、そのことをアスペ先生が実験で確認したのです。
この85%戦略を「白黒のボールだけでなんとなく」説明できると良かったのですが、残念ながらそれほど簡単な話ではありません。$(2+\sqrt 2)\div 2$という数字は$cos^3(𝜋/2)$のことなのですが、これを「なんとなく説明する」のはちょっと無理と言うものなのですよ。
白黒のボールだけでなんとなく説明できるCHSH風ゲーム
しかし、幸いなことに、ルドルフ先生はCHSHゲームのルールを変更して、「白黒のボールだけでなんとなく」説明できるようにしてくれています。ここでは、それを使って説明します。ルールは以下の通りです:
- コインが両方とも裏の時に、2人とも黒と言えば勝ち。
- コインが両方とも表の時に、2人とも黒と言ってしまったらゲーム終了
- コインの片方だけが表の時に、表と伝えられたプレイヤーが白、もう1人が黒と言ってしまったらゲーム終了
- これを4000回繰り返すまでに20回勝てたら100万ドル貰える
| 白白 | 白黒 | 黒白 | 黒黒 | |
|---|---|---|---|---|
| 表表 | ー | ー | ー | 終了 |
| 裏表 | ー | ー | 終了 | ー |
| 表裏 | ー | 終了 | ー | ー |
| 裏裏 | ー | ー | ー | 勝ち |
よく考えてみると、プレイヤーにとって非常に厳しいルールだとわかります。
勝つためには裏裏の時に、2人そろって黒と言わなければなりません。すると各自は裏の時には黒と言わなければなりません。黒黒と言い続けると表表の時に終了してしまうので、表の時に黒というのは危険です。と言って、白と言ってしまうと、相方が裏なら黒と言うので、終了してしまいます。
結局、最良の戦略は、アリスは常に黒と言う、ボブは裏の時は黒、表の時は白か黒かを勘に任せて言う、ことでしょうか。そして、20回裏裏が出るまでの間、ボブの勘に頼ってゲーム終了にならないことを祈るのです。
毎回1/4の確率で起こる「ゲーム終了」をかわしながら、勝ち星を20個獲得しなければなりません。賞金が100万ドルなのも不思議ではありませんね。
量子もつれを使った必勝法
このゲームに「量子もつれ」を使って挑むことができれば、非常に有利にできる戦略、少なくとも絶対に途中でゲーム終了にはならない戦略があります。
- (白白+白黒+黒白)のようにもつれたボールのペアを4000セット作っておく。
- 各ペアの左右を別の保管箱にしまい、ペアがわかるように1~4000の番号を保管箱に書いておく。同じ番号の2つの保管箱に、もつれているペアの片方ずつが入っている。
- アリスはペアの左側の保管箱4000個とアダマール箱4000個を東京に、ボブはペアの右側の保管箱4000個とアダマール箱4000個をニューヨークに運んでゲームに挑む。
- 2人は持ち込んだ保管箱を番号順に使う。
- 2人は、表が出たら保管箱の下から出てきたボールの色を言う。裏が出たら保管箱の下にアダマールを接続して、アダマールから出てきたボールの色を言う。
この戦略でどうして絶対にゲーム終了にならないのでしょうか。
表表の場合
2人が持っているペアは(白白+白黒+黒白)ですから、2人の回答はこの3種類です。黒黒という回答はしないのでゲーム終了にはなりません。
これは当たり前に思えますね。「もつれたボール」なんて奇妙なものを使わなくても、白白、白黒、黒白の3通りのペアをランダムに4000個作って、2つずつの保管箱に入れておけばいいわけです。どこにも不思議なことはありません。
裏表の場合
アリスはアダマールを使います。アダマールは白を(白+黒)に、黒を(白-黒)に変化させることを思い出してください。すると、結果は以下になります。
((白+黒)白+(白+黒)黒+(白-黒)白)
=(白白+黒白+白黒+黒黒+白白-黒白)
=(白白+白黒+黒黒+白白)
黒白の可能性が消えました。黒白という回答はしないのでゲーム終了にはなりません。
これはとても不思議なことです。ボブは何もしていません。遠く離れたアリスがアダマールを使ったことも知りません。なのにボブのボールは、アリスが黒の時は必ず黒になってしまいました。
表裏の場合
裏表と同様です。
(白(白+黒)+白(白-黒)+黒(白+黒))
=(白白+白黒+白白-白黒+黒白+黒黒)
=(白白+白白+黒白+黒黒)
白黒の可能性が消えて、ゲーム終了にはなりません。
裏裏の場合
((白+黒)(白+黒)+(白+黒)(白-黒)+(白-黒)(白+黒))
=(白白+白黒+黒白+黒黒+白白-白黒+黒白-黒黒+白白+白黒-黒白-黒黒)
=(白白+白白+黒白+白白+白黒ー黒黒)
4種類の回答すべての可能性があります。勝てる黒黒が出る確率はいくつでしょうか? 直感的には$1/6$に思えますね。でも、もつれたボールが特定の色の組み合わせになる確率は、2乗に比例するという規則があります。ここでは白白になるには3つの可能性があり、他は1つずつなので、白白になる確率は$3^2\div(3^2+1^2+1^2+1^2)=9\div 12=3/4$、他の組み合わせになるのは$1/12$になります。
4000回繰り返しても途中では絶対にゲーム終了にはならないのですから、十分に勝ち目はあります。4000回のうち平均して1000回は裏裏でしょうから、その$1/12$の83回は勝てそうです。賞金100万ドルはほぼ確実ですね。
必勝法の準備
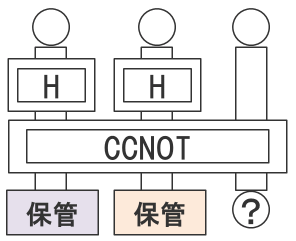
さて、そもそも(白白+白黒+黒白)というペアをどうやって作るのか、という話が残っていました。これは下の図のように、アダマール2つとCCNOTを使います。CCNOTは前回・前々回で説明したCNOTの拡張版で、左側の2つが両方とも黒ならば右端のボールの色を反転させます。したがって、下から出てくる3つのボールは、(白白白+白黒白+黒白白+黒黒黒)になります。
この回路の特徴は、左側2つのボールだけを保管箱に入れて、右端のボールは観測してしまうことです。もし、右端のボールが黒ならば、保管箱に入っているのは両方とも黒なので、これは捨ててしまいます。右端のボールが白ならば、保管箱に入っているのは(白白+白黒+黒白)というもつれたペアのはずです。
というわけで、このゲームを実際にやってみて、アリスとボブにまんまと100万ドル差し出す羽目になったら、「EPRパラドックス」はパラドックスではなくて現実に起こる現象なのだと納得するしかありませんね。
おまけ:Bellの不等式の少し詳しい解説
ベル先生は、東京とニューヨークでの観測結果の相関関係について次のように定式化しました。
まず、東京の箱を開けた時、白が出るか黒が出るかを決める関数$A(s,x)$があるとしました。$x$はアインシュタイン大先生が言う隠れた変数で、存在はするけど知られていません。$s$は$x$以外の知られている任意の変数集合です。最初に左側に入れたボールが白なのか黒なのかとか、東京まで運ぶ時に箱の向きを変えなかったのか変えたのかとか、箱を開ける時に蓋を上にして開けたのか横に倒して横から開けたのかとか、はたまた、運ぶ時の気温や振動や開ける時の天候とか、観測に関係ありそうなどんな物理変数でもいくつでも$s$に含めてかまいません。$A(s,x)$が$1$であれば「白」、$-1$であれば「黒」が出ることを表します。同じようにニューヨークの箱を開けた時に白が出るか黒が出るかを決める関数を$B(s,x)$とします。
隠れた変数$x$の値は、2つの箱を設定した時になんらかの方法で決まっていて、離れた場所に運ばれても変化しません。この$x$のお陰で、あたかも超光速に情報が伝わるように見えているのです。
一方、$s$には任意の物理変数を含めてよいので、箱を開ける瞬間に変更できます。例えば、箱を北に向けてから開けるのか、南に向けて開けるのか、とか。別の箱を下に接続してから開けるとか。ここでは、そのような開け方のうち、東京とニューヨークとでそれぞれ2通りずつのどちらかを選んで開けるものとします。東京の開け方を$s=a$と$s=a’$、ニューヨークの開け方を$s=b$、$s=b’$とします。
次に2つの観測結果の相関係数を定義します。量子力学での相関係数は、統計学の相関係数とは定義が違うので注意が必要です。相関係数$C(a,b)$は、東京で$a$の開け方、ニューヨークで$b$の開け方をした時、両方とも同じ色である確率と違う色である確率の差です。
これを数式で定義すると$$C(𝑎,𝑏)=\sum{𝐴(𝑎,𝑥)𝐵(𝑏,𝑥)𝑝(𝑥)}$$になります。$p(x)$は隠れた変数$x$の確率分布です2。$𝐴(𝑎,𝑥)𝐵(𝑏,𝑥)$は同じ色の時は$\pm 1\times\pm 1=1$、違う色の時は$\pm 1\times\mp 1=-1$になるので、それぞれの差が計算できるわけです。
ベルはこの相関係数を使ってある不等式を導いたのですが、それにはある適用条件がありました。この適用条件を緩めて一般化したのが、 John Clauser、Michael Horne、Abner Shimony、Richard Holtの4人で、頭文字を取ってBell-CHSHの不等式と言います:$$C(𝑎,𝑏)+𝐶(𝑎′,𝑏)+𝐶(𝑎,𝑏′)−𝐶(𝑎′,𝑏′)\leq 2$$
この式が重要なのは実験で確認できることです。もつれた量子のペアを多数用意して、それぞれを2通りの方法で観測してみて、同じ色になった回数、違う色になった回数を計測すれば上の式を計算できます。それがもし2より大きくなることがあると、隠れた変数の存在が否定されるのです。
Bell-CHSH不等式の直感的な証明
$C(𝑎,𝑏)+𝐶(𝑎′,𝑏)+𝐶(𝑎,𝑏′)−𝐶(𝑎′,𝑏′)$
$=\sum{𝐴(𝑎,𝑥)𝐵(𝑏,𝑥)𝑝(𝑥)}+\sum{𝐴(𝑎',𝑥)𝐵(𝑏,𝑥)𝑝(𝑥)}+\sum{𝐴(𝑎,𝑥)𝐵(𝑏',𝑥)𝑝(𝑥)}-\sum{𝐴(𝑎',𝑥)𝐵(𝑏',𝑥)𝑝(𝑥)}$
$=\sum{(𝐴(𝑎,𝑥)𝐵(𝑏,𝑥)+𝐴(𝑎',𝑥)𝐵(𝑏,𝑥)+𝐴(𝑎,𝑥)𝐵(𝑏',𝑥)-𝐴(𝑎',𝑥)𝐵(𝑏',𝑥))𝑝(𝑥)}$
$=\sum{(𝐴(𝑎,𝑥)(𝐵(𝑏,𝑥)+𝐵(𝑏',𝑥))+𝐴(𝑎',𝑥)(𝐵(𝑏,𝑥)-B(𝑏',𝑥)))𝑝(𝑥)}$
ここで特定の$B(b,x)$と$B(b’,x)$はそれぞれ$\pm 1$なので、$(𝐵(𝑏,𝑥)+𝐵(𝑏′,𝑥))$か$(𝐵(𝑏,𝑥)−𝐵(𝑏′,𝑥))$のどちらかは$0$で、もう1つは$\pm 2$です。$A(a,x)$と$A(a’,x)$もそれぞれ$\pm 1$なので、$$𝐴(𝑎,𝑥)(𝐵(𝑏,𝑥)+𝐵(𝑏′,𝑥))+𝐴(𝑎′,𝑥)(𝐵(𝑏,𝑥)−𝐵(𝑏′,𝑥))=\pm 2$$
したがって
$$C(𝑎,𝑏)+𝐶(𝑎′,𝑏)+𝐶(𝑎,𝑏′)−𝐶(𝑎′,𝑏′)\leq\sum{2p(x)}\leq 2$$
CHSHゲームの勝率の限界
Bell-CHSH不等式が成り立つ場合、つまりアインシュタイン大先生の言うように隠れた変数が存在する場合の、CHSHゲームの勝率の最大値は75%になります。
コインが表表、裏表、表裏、裏裏の時の勝率をそれぞれ$P_{hh}$、$P_{th}$、$P_{ht}$、$P_{tt}$とします。全体の勝率$P$は以下になります:
$$P=\frac{P_{hh}+P_{th}+P_{ht}+P_{tt}}{4}$$
表表の時は同じ色であれば勝ちでした。その時、アリスとボブはそれぞれ$a$と$b$という開け方をします。相関係数$C(a,b)$は同じ色を言う確率と違う色を言う確率の差なので、$$C(a,b)=P_{hh}-(1-P_{hh})=2P_{hh}-1$$同様に$$C(a',b)=2P_{th}-1$$$$C(a,b')=2P_{ht}-1$$裏裏の時だけは違う色であれば勝ちでしたので$$C(a',b')=(1-P_{tt})-P_{tt}=1-2P_{tt}$$これをBell-CHSH不等式に代入すると
$$C(𝑎,𝑏)+𝐶(𝑎′,𝑏)+𝐶(𝑎,𝑏′)−𝐶(𝑎′,𝑏′)=2(P_{hh}+P_{th}+P_{ht}+P_{tt})-4=8P-4\leq 2$$したがって、$P\leq (2+4)\div 8=0.75$になります。