はじめに
私の量子コンピュータ(ゲート型)の知識は、主に丸山不二夫先生のレクチャーと、先端IT活用推進コンソーシアムの勉強会によるものです。丸山先生の3月のセミナー「量子コンピュータをやさしく理解する三つの方法」で、テリー・ルドルフ教授のQ is for Quantumという本を紹介いただき、面白そうなので買ってみました。Kindle版884円です。
これがなかなか良い本で、“ブロッホ球”とか“テンソル積”とか“ユニタリ変換”とか、まったく使わないで、「なんとなくそんなものか」と分かるものなのです。「これは超初心者向けに使えるのではないか」と思い、試しに社内の勉強会で話してみたら結構ウケたので、気を良くしてここで披露してみることにしました。
量子の不思議な振る舞い
「量子」とは、「最小単位があるくせに波であるかのように振る舞うもの」です。例えば、光は量子です。光は「光子」という最小単位があるくせに、波であるかのような振る舞いをします。光は粒子なのか波なのか、というお馴染みの議論ですね。なぜそんなことが起こるのか、長年研究されているのですが、本当のところは誰にも分かっていないようです。ただこう考えれば辻褄が合うよねという考え方が提唱・合意されているだけらしいのです。上記のルドルフ教授の本が説明しているのも、その「辻褄が合う考え方」の一つです。
辻褄を合わせないといけない不思議な振る舞いとして有名なものとして「ヤングの実験」があります。詳しくはWikibooksとかを見ていただきたいのですが、すごく簡単に言うと「2つの光を重ねると縞模様が見える」ということです。粒子であれば単純に強め合うはずですが、縞模様になるということは強め合ったり打ち消し合ったりする、ということが起きているのです。
また、「マッハ・ツェンダー干渉計」という不思議な話もあります。詳しくはこちら(下図はここから引用)あたりを見ていただきたいのですが、後で参照するので少し説明しておきます。
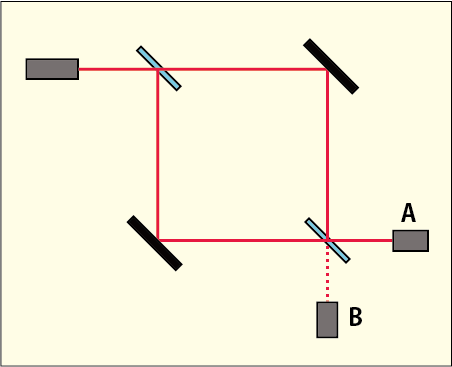
図のように、マッハ・ツェンダー干渉計は7つの部品で構成されます。左上の横長の箱は光子銃で光子を一発ずつ発射します。4つの斜めの部品のうち、灰色の2つはハーフミラーで、光子を50%の確率で反射したり透過したりします。黒い2つは普通のミラーです。右下のAとBは光子の検出器です。
まず、右下のハーフミラーを外してから、光子を何発か発射してみます。すると、光子はAとBの検出器に半々に分かれて到達します。左上のハーフミラーがちゃんと50%ずつに振り分けていることがわかります。次に、右下のハーフミラーを戻してみると、光子は検出器Aにしか届かなくなります。右下のハーフミラーは、光子が上から来たら反射、左から来たら透過しているように見えますね。ところが、光子銃の位置を変えて、左上のハーフミラーの上から光子を発射すると、今度は検出器Bにしか届かなくなるのです。**右下のハーフミラーは、光子銃が左にあったのか上にあったのかどうしてわかったのでしょう?**さらに、ハーフミラーとミラーで作られる四角形のどこか一箇所を遮ってみます。すると、光子は両方の検出器に半々に分かれて到達するのです。光を束で通しているのであれば、さきほどの「強め合ったり打ち消し合ったり」してるのかな、とも思えそうですが、一つの光子だけでもこうなるのです。不思議ですよね。
白黒のボールによるコンピュータ回路の理解
さて、ルドルフ先生の説明方法は、コンピュータ回路を「白黒のボールを入れるとボールが出てくる箱」でイメージする、というものです。例えば、下の図は「NOT」と呼ばれる回路です。
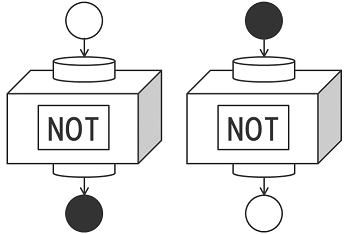
「NOT」というラベルが付いた箱の上から白いボールを入れると下から黒いボールが出てきて、黒いボールを入れると白いボールが出てきます。この最初の図は3次元の箱で書いていますが、以降では面倒なので2次元で書きますね。実は、ルドルフ先生の本もそうなんです。
次の図は「SWAP」と呼ばれる回路で、入力が2つ、出力も2つあって、左右を入れ替えます。
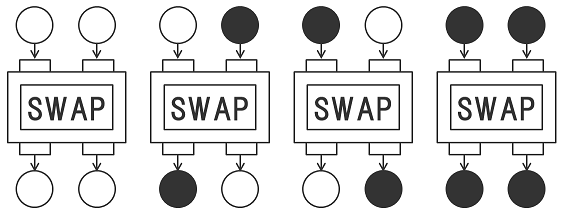
次の図は「CNOT」というちょっと変わった回路です。こいつが後々色んなことを起こす、量子コンピュータの世界では主役の一人です。どういう規則で出力しているか、ちょっと考えてみてください。
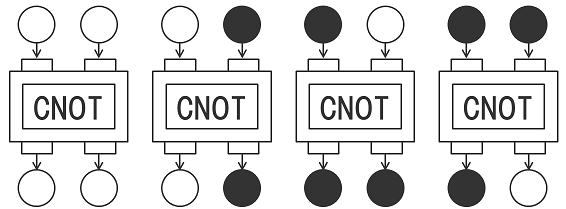
分かりましたか? 実はこれはIF文の一種なのです。まず、左のボールは常に素通しです。問題は右のボールですが、もし左のボールが白ならば、右のボールもそのまま通します。そして、左のボールが黒の時は、右のボールの色を変えます。
さて、これらの回路はさらに連結させることで、より大きな回路を作ることができます。例えば、下の図は、NOT回路を直列に重ねたものです。色が2回反転されて元に戻るわけですね。
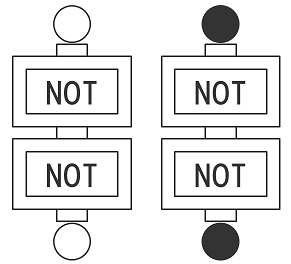
不思議な量子回路
さて、ここに不思議な働きをする「アダマール」と呼ばれる回路があります。アダマール(Hadamard)は19世紀のフランスの数学者で、この業界(どの業界?)では頭文字をとって「H」で表現するのが普通です。
ちなみに、ルドルフ先生の本では先生のお友達のPeteさんにちなんで「PETE」と書いています。どのPeteさんか分かりませんが、もしかしたら後で説明する予定の「ショアのアルゴリズム」のPeter Shor先生のことかしら、と思います。とはいえ、この記事では一般的な名称のアダマール(H)を使っておきます。
アダマール回路は以下の図のように、白いボールを入れ続けても、黒いボールを入れ続けても、半々の確率でランダムに白と黒のボールが出てきます。
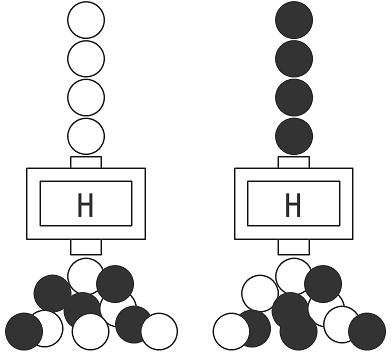
単なるランダム回路かな、と思ってはいけません。下の図のようにアダマールを2つ重ねると、不思議なことに入力したボールと同じ色のボールが必ず出てくるのです。
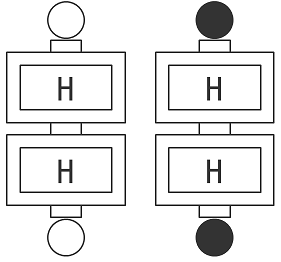
下のアダマールは、上のアダマールの入力が白だったのか黒だったのかどうしてわかったのでしょう?
気が付きましたか?そうです、この不思議な現象は、先ほど説明したマッハ・ツェンダー干渉計で起こる現象と同じなのです。
さらに不思議なことが起こります。2つのアダマールの間を少し隙間を空けて、懐中電灯で照らして覗き込んでみます。上からは白いボールだけを連続して入れ続けます。
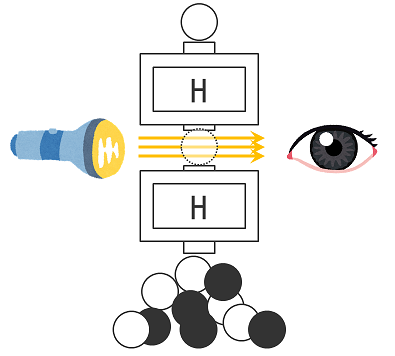
すると、隙間を白と黒のボールがランダムに流れ落ちていくのが見えるのですが、この時には下のアダマールからはランダムに白と黒のボールが出てくるのです。
そして、懐中電灯を消して途中の流れが見えなくなると、なんと、白いボールしか出てこなくなります。
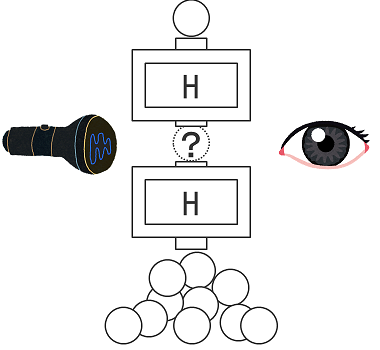
この現象は、マッハ・ツェンダー干渉計でどこかを遮ると次のハーフミラーの効果がランダムになる現象と似てますね。
この「見たり見なかったりすると結果が変わる」というのが、量子のとても重要な性質なのです。
こう考えれば辻褄が合う(量子の重ね合わせ状態)
このアダマールの不思議な性質を、ルドルフ先生は下の図のように説明しています。
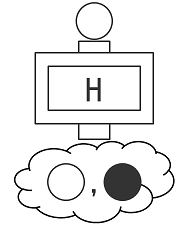
アダマール回路から出てくるのは、雲に包まれたボールです。雲の中では白と黒が混ざりあった状態なのですが、それを見る(観測する)とその瞬間に白か黒か決まります。
ちなみにルドルフ先生は「雲(クラウド)って呼びたかったけど、クラウドコンピューティングと紛らわしいから、霧状態(Misty state)と呼ぶことにする。うちの父親なら、そりゃMist-eriousだな、って言うかもね」と書いてました。
で、この記事では雲を書くのが面倒なので、以下の図のように雲を括弧“( )”で、カンマを“+”で書くことにします。
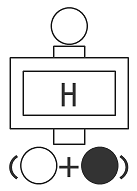
さて、アダマールに白いボールを入れると上の図のような霧状態のボールが出てくるのですが、黒いボールを入れた時は、これとはちょっと違って下の図のようになります。
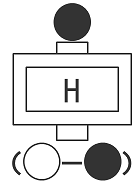
ルドルフ先生はこれを「白いボールとネガティブな黒いボールが混ざりあった状態」と説明します。これを観測するとやはりその瞬間に白か黒に決まるのですが、その黒がもともと普通の黒だったのか、ネガティブな黒だったのかは分かりません。
ちょっと怪しくなってきましたね。「それって、ようはどういうこと?」と思えてきます。ですが、なぜそんなことが起こるのか、本当のところは誰にも分かっていないことなので、「そういうものか」と思っておきましょう。
では、そう考えるとどう辻褄が合うのか、アダマールを2つ重ねた場合について見てみましょう。
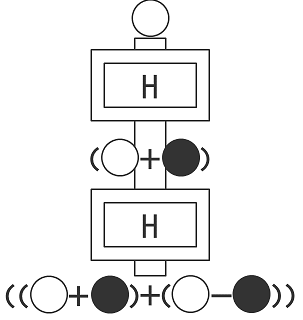
上から白いボールを入れると上側のアダマールからは白と黒が混ざりあった状態のボールがでてきます。これが下側のアダマールに入ると、下からは「白と黒が混ざりあった状態」と「白とネガティブな黒が混ざりあった状態」が混ざりあった状態のボールが出てきます。この時、白と白は強め合い、黒とネガティブな黒は打ち消し合うので、結果として白いボールが出てきます。
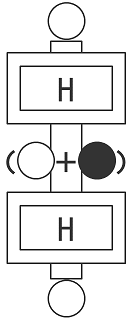
量子は波の性質を持つので強め合ったり打ち消し合ったりするのです。
上から黒いボールを入れるとどうでしょう。下側のアダマールには白とネガティブな黒が混ざりあった状態のボールが入るので、下から出てくるのは「白と黒が混ざりあった状態」とネガティブな「白とネガティブな黒が混ざりあった状態」が混ざりあった状態のボールが出てきます。
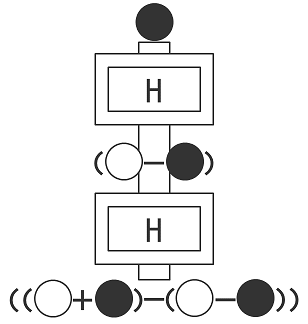
ネガティブな「白とネガティブな黒」は、ネガティブな白と普通の黒として作用します。白とネガティブな白は打ち消し合い、黒と黒は強め合うので、結果として黒いボールが出てきます。
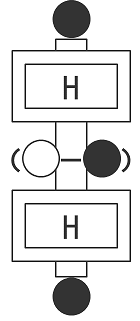
これで辻褄が合いました。
「それって、どういうこと?」と考えないで、「そういうものか」と思っておきましょう。
量子のもつれ(エンタングルメント)
アインシュタイン大先生が量子論に懐疑的だったことは有名です。アインシュタイン先生は1935年に「そんな辻褄合わせだと、ありえないことが起こることになってしまうぞ」と主張して、次のような思考実験を披露しました。
下の図のように、アダマールとCNOTを重ねて、白い2つのボールを同時に入れます。アダマールには入り口が一つしかないので、右側のボールは直接CNOTの右側に入れます。
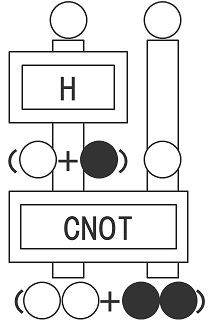
アダマールからは白と黒が混ざりあった状態のボールが出てきてCNOTの左側に入ります。CNOTはそれが白ならば右の白いボールをそのまま、黒ならば右のボールを黒いボールに変えて出します。したがって、下から出てくるのは「白・白」と「黒・黒」が混じり合った状態の2つのボールが出てきます。この2つのボールは観測した瞬間に、白と白、また黒と黒に半々の確率で決まります。
それでは、観測してしまわないように左右のボールをそれぞれ保管箱に入れておきましょう。そして、左の箱を東京に運び、右の箱をニューヨークに運びます。
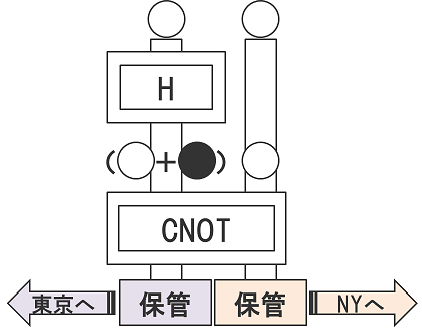
ここで誤解しやすいのですが、東京の箱に白・白が、ニューヨークの箱に黒・黒が入っているわけではありません。それぞれの箱には白か黒かが決まっていないボールが1つずつ入っています。そして、東京の箱を開けて観測すると白か黒かが決まるのですが、その瞬間同時にニューヨークの箱の中身も同じ色に決まるのです。右の箱をニューヨークではなく月面に運んでも、東京と同じ瞬間に色が決まります。ヤマトでイスカンダルに運んでもそうなります(古い!)。「これは光の速さを越えて情報が伝わることになるのでパラドックスだ、量子論はまだ不十分な理論であり、“隠れた変数”が存在するに違いない」とアインシュタイン大先生は主張しました。
このように2つのボールの色が、片方を観測すると同時にもう片方も決まってしまうことを、量子がもつれている、と言います。もつれている量子の色は、どんなに遠く離れていても同時に決まります。
(白・白+黒・黒)は典型的な「もつれている量子」の例ですが、(白・黒+黒・黒)はもつれていません。左をいつ観測しようが、右は常に黒だからです。これは「(白・黒+黒・黒)=(白+黒)・黒」のように考えれば分かります。
そうそう、それでアインシュタイン大先生が主張した隠れた変数の顛末ですが、1964年に理論的に、1982年に実験的に否定されてしまいました。右のボールの色は時空を超えて決まるのかもしれませんが、箱を開けて見るまでは本当にそうか分からないのですから、パラドックスではないと言えないことはないですね。こんにちでは「そういうものなのだ」と理解されるようになったようです。
量子コンピュータによる超高速並列計算
そもそも量子コンピュータは、ムーアの法則が限界まで来た古典コンピュータを凌ぐ、超高速計算機として期待されています。
ここではその例として「AND」回路を説明します。ANDは皆さんご存知のように、2つの論理変数の両方ともtrueの時にtrue、それ以外ではfalseを返す回路です。そこで、白いボールをfalse、黒いボールをtrueとみなすと、AND回路は以下の図のようになります。
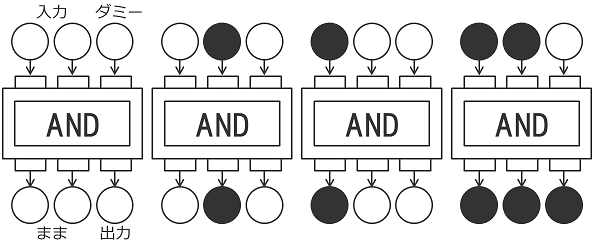
ここで重要なことは、量子回路は入力と出力の数が同じでなければならないということです。ANDは2入力・1出力なので、このような場合には3つの入出力を設けて、左の2つは入力に使い、右の1つを出力に使います。右の一つにはとりあえずダミーとして白いボールを入れておきます。また、左の2つの出力は、入力したボールと同じ色のボールが出てきます。これで、黒いボールが2つ入った時だけ右から黒いボールが出ていくるAND回路になります。
それでは、AND回路の左の2つに「白と黒が混ざりあった状態のボール」を入れるとどうなるでしょう。3つのボールはもつれてしまい、下からは「白・白・白」と「白・黒・白」と「黒・白・白」と「黒・黒・黒」が混ざりあった状態の3つのボールが出てきます。
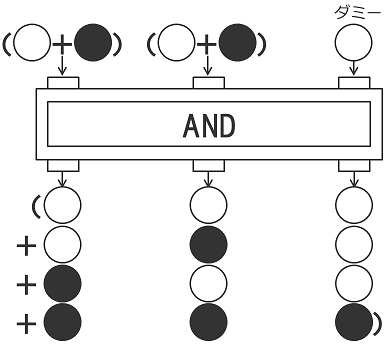
4通りの計算が同時並行して実行されました。この例では入力が2つでしたが、もし10個だったら2の10乗=1024通りの計算を、もし100個だったら12穣6757予600垓2282京通り以上の計算を同時並行して同じ時間で実行します。こんなコンピュータができたら、どんな計算でも一瞬で終わりそうですね。
超高速計算のまやかし
前の節の説明で素直に納得された方、あなたは騙されています(笑い)。
量子コンピュータは、古典コンピュータで動いていたどんなアルゴリズムでも指数関数的に高速化する、わけではありません。なぜでしょう?
たしかにAND回路の下には4通りの計算結果が混ざりあった状態のボールが出てきています。でも、その結果を知るためには観測しなければなりません。観測したら、ランダムな状態が1つに収束するので、4通りのうちの一つだけが分かります。では4回観測すればいいのでしょうか?どの1つが観測できるかはランダムなのですが、ラッキーなことに4通りの1つずつを観測できたとしましょう。でも、そうするためには回路を4回使いました。つまり4倍の時間がかかっています。それなら古典回路を使った方が、ランダム性が無い分だけマシですね。
量子コンピュータは膨大な数の並列計算を1回分の時間で実行してしまいますが、その膨大な数の計算結果を一つ一つ取り出すのではなく、なんらかの方法で意味を見出す必要があります。そのような特殊なアルゴリズムが量子アルゴリズムです。量子アルゴリズムは、現在盛んに研究されていますが、この記事を書いている時点では61個が知られています。
この記事の最後に、量子アルゴリズムの中でおそらく最も有名な「ショアのアルゴリズム」を簡単に説明しておきますが、「超々入門」とはさすがに言い難いので「付録」とします。
おわりに
アメリカの著名な物理学者、リチャード・ファインマン先生は大学の物理学の講義でこう述べたそうです:
If you think you understand quantum mechanics, you don't understand quantum mechanics.
ということなので、量子のことを分かった気になる必要は無さそうです。「そういうものなのだ」「そう考えれば辻褄が合うのだ」と思っておくことにしましょう。
追伸
実はあと「量子テレポーテーションを白と黒のボールで説明する」というネタも用意していたのですが、あまりに長い記事になってしまったので割愛します。この記事に人気が出たら、続編として書くかもしれません(アドベントカレンダーの穴埋めとして書かされるかも ^o^) 弊社アドベントカレンダーの最後の記事として投稿しました。
付録:量子アルゴリズムの例(ショアのアルゴリズム)
ショアのアルゴリズムを使えば「暗号が解読できる」と知られていますね。正確に言うと、ショアのアルゴリズムは素因数分解を高速に実行するアルゴリズムです。そして、素因数分解ができれば、例えば公開鍵暗号を簡単に解読できます。
まず、公開鍵暗号についてですが、「RSA 暗号がようやく分かった気がしたのでまとめてみる」がワタシ的にはわかりやすかったので、詳しくをそちらを見ていただくとして、ここではざっくりと説明しておきます。
例えば$0~32$の数をこっそり送ってもらいたいとします。この時、相手には「送る数字を$7$乗して$33$で割った余りを送ってください」と頼みます。例えば、送る数字が$4$ならば「$4^7=$ $16384=$ $33\times 496+16$」なので、$16$が届きます。あなたは、届いた数字を$3$乗して$33$で割った余りを見れば「$16^3=$ $ 4096=$ $33\times 124+4$」、元の数字が$4$と分かります。これは「$0~32$の数を$7$乗して$33$で割った余りを、$3$乗して$33$で割った余りは、元の数字と同じ」という性質を使っています。他の数字でも試してみてください。
$33$と$7$という数字は公開している(公開鍵)ので、$3$という数字(秘密鍵)を知られないことが大事です。しかし、「$33=3\times 11$」であることが分かれば、それと$7$とから秘密鍵が$3$であることは簡単な計算で分かってしまいます。そこで、公開鍵暗号では非常に大きな素数2つを掛け算した値を公開鍵として使います。だいたい100桁X100桁くらいだと今どきのスパコンなら素因数分解できてしまうそうなので、150桁X150桁~500桁x500桁の公開鍵を使うことが推奨されています。ところが、ショアのアルゴリズムを使った量子コンピュータならば、この素因数分解ができてしまうのです。
ショアのアルゴリズムは、整数の割り算の余りについての面白い性質を利用します。例えば、$2^0, 2^1, 2^2, 2^3, \dots$を$15$で割った余りを見てみましょう。
| $x$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
| $2^x$ | $1$ | $2$ | $4$ | $8$ | $16$ | $32$ | $64$ | $128$ | $256$ | $512$ | $1024$ |
| 余り | $1$ | $2$ | $4$ | $8$ | $1$ | $2$ | $4$ | $8$ | $1$ | $2$ | $4$ |
$1,2,4,8$と4つずつ繰り返していることがわかります。これを数学では「$15$を法とする$2$の位数は$4$である」と言います。そして「$N$を法とする$z$の位数が$2r$だったとき、$z^r+1$または$z^r-1$と$N$とに、1でない最大公約数(GCD)があれば、それが$N$の素因数である」という性質があります。$15$と$2$の例では位数が$4$なので、$2^2+1=5、GCD(5,15)=5$、また$2^2-1=3、GCD(3,15)=3$なので、$15$が$5$と$3$に素因数分解できました。
別の例として$221$を考えましょう。皆さんはパッと素因数分解できますか?
$221$を法とする$4$の位数は$12$です。すると$4^6+1=4097$、$GCD(4097,221)=17$、また$4^6-1=4095$、$GCD(4095,221)=13$となって、$221$が$17$と$13$に素因数分解できました。
$221$の約数を発見するには、基本的には$221$を$2, 3, 4, \dots, 14$で割ってみるしかありません。一方、$221$を法とする$4$の位数を求めるにも、$4^0, 4^1, 4^2, 4^3, \dots, 4^{12}$を$221$で割ってみなければなりません。どちらも同じくらい大変そうです。しかし、ショアのアルゴリズムはこの位数を高速に計算するアルゴリズムなのです。
$221$だと図が大きくなるので、$15$の場合を下に図示します。今回は白いボールを$0$、黒いボールを$1$だとみなし、その並びを2進数と考えます。入力数と出力数をそれぞれ4つとして、入力された4つのボールを2進数と見た数だけ$2$のべき乗を求め、それを$15$で割った数を2進数で表現したボールを出力する回路を作成します。
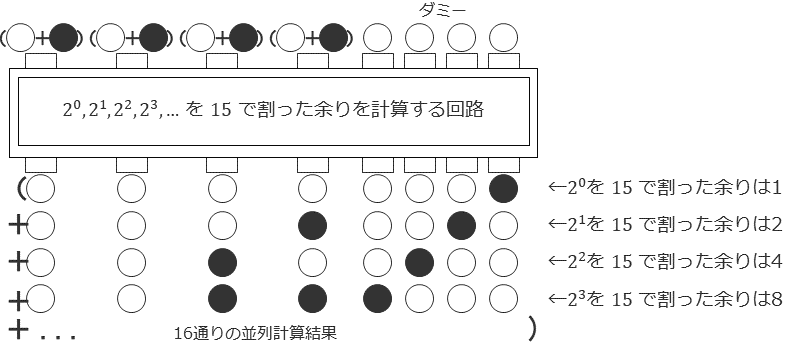
この回路に、4つの「白と黒が混ざりあった状態のボール」を入力すると、$2^0$から$2^{15}$までの16通りの計算を一度に並列に実行して、16通りの結果が得られます。さて、この回路の出力を観測するとどうなるでしょうか?
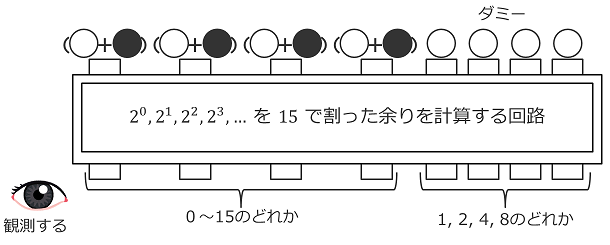
左の4つの出力には、$0~15$を表す2進数のどれか一つが観測できます。この時、右の4つの出力には、$1,2,4,8$のどれかしか観測されません。これを何回か繰り返します。例えば、右側に$8$が観測された時、左側で$3$と$7$を観測したとします。これを「$3\cdot 8$と$7\cdot 8$を観測」と書くことにしますが、この2つだけで位数が$2$か$4$だろうと分かります。そして、さらに$1\cdot 2$を観測できれば位数は$2$ではなく$4$だと分かります(もし位数が$2$なら$3\cdot 8$ではなく$3\cdot 2$になるはず)。
そんな行き当たりばったりでいいのか?と思う方のためにもう少し説明しますが、さらに小難しい話になるので覚悟をお願いします。
実は、ショアのアルゴリズムにはまだ先があります。上の図では全部の出力を観測してしまいましたが、右半分だけ観測した場合にどうなるか考えてみましょう。例えば、右半分を観測したら$8$だったとします。この時、左半分は$3、7、11、15$の重ね合わせ状態になります。一般に、右半分を観測すると左半分は「位数毎に飛々の値の重ね合わせ状態」になっています。そういう「一定の間隔で飛々になっている重ね合わせ状態」を量子フーリエ変換という回路に通してから観測すると、(観測した値$\times$間隔)が全状態数の倍数になるという法則があります。例えば上の回路で、右半分を観測した後で左半分を量子フーリエ変換し、その結果を観測すると$0、4、8、12$がランダムに観測できます。全状態数は$16$なので、$0、4、8、12$に同じ数を掛けて$16$の倍数になるのは、と考えると位数は$4$だと分かります。
ここで紹介したのは8量子ビットの小さい例で、実際の量子コンピュータで検証されたものも現時点ではこれくらいのサイズです。この程度の計算だと、何度も量子計算を実行して$0、4、8、12$を見つけるよりも、$2$から順番に割り切れるかどうか試した方がずっと早いですね。
しかし、実用上の公開鍵暗号では、$N=150$桁素数$\times 150$桁素数$=300$桁$\ \fallingdotseq 1000$ビット以上を利用するので、これを$2$から順に割り算して行くには$2^{1000}$通り程度の計算が必要です。一方で、量子アルゴリズム「ショアのアルゴリズム」を使うと$1000^2$通り程度で済むそうなのです。