はじめに
この記事はMachine Learning Advent Calendar 201612/14のエントリーです.
今回は2標本問題について扱います(統計じゃん!というツッコミが入りそう.後半からはカーネル法です).
2標本問題では独立な2つの母集団からそれぞれ
$X_1,...,X_l$, $Y_1,...,Y_n$ というように合計$N=\ell+n$のサンプルが得られたとき,これらのサンプルが得られた2母集団の分布が同じかどうかという問題を考えます.
たとえば,臨床試験などで投薬を行った群と行わなかった群で薬の効果に差があったかどうか,2つの学校の試験の点数が同じかどうかといったことを検証したい際に用いることができます.マーケティングなどにおけるA/Bテストの結果の検証でも用いることができるでしょう.
今回はこの問題に対する様々なアプローチを紹介していきたいと思います.この記事内ではなるべく概念的な説明にとどめて,各手法のイメージやモチベーション,Rでの使い方を紹介したいと思います.もう少し数学的な詳細が知りたい方は,参考文献のリストを参照してください.また私が以前作成したスライド(英語)
には本記事には載せていない各手法の性能比較などを載せているので興味のある方は確認してください.
2標本問題の定式化
$X_1,...,X_l \stackrel{{i.i.d}}\sim P$, $Y_1,...,Y_n \stackrel{{i.i.d}}\sim Q$と考えて, 帰無仮説を$P=Q$, 対立仮説を$P\neq Q$とします.いくつもの解法が考えられます.大きな枠組みではパラメトリックな検定とノンパラメトリックな検定に分けることができます.以下でこれらを説明していきます.
パラメトリックな2標本検定
まずはパラメトリックなアプローチが考えられます.2つの分布の形を仮定して,そのモーメントを比較する方法です.有名なものでサンプルが正規分布に従うと仮定したスチューデントのt-検定やウェルチのt-検定,F検定などがあります(t-検定ではサンプルサイズが大きければ正規分布である必要はありません).大学で統計の授業を取っていた方はご存知でしょう.
Rでは次のようにします.
# 平均も分散も異なる正規分布から100個ずつサンプリング
x <- rnorm(100,0,1)
y <- rnorm(100,1,3)
# t-検定とF-検定
t.test(x,y,var.equal = FALSE)
var.test(x,y) #等分散の検定
Welch Two Sample t-test
data: x and y
t = -3.557, df = 120.87, p-value = 0.0005366
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-1.8102522 -0.5156762
sample estimates:
mean of x mean of y
0.05884905 1.22181322
F test to compare two variances
data: x and y
F = 0.11183, num df = 99, denom df = 99, p-value < 2.2e-16
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.07524339 0.16620444
sample estimates:
ratio of variances
0.1118293
p値はどちらも0.05以下となり有意水準0.05でどちらも同分布ではないということが検出できました.しかし,次のような場合はどうでしょうか.
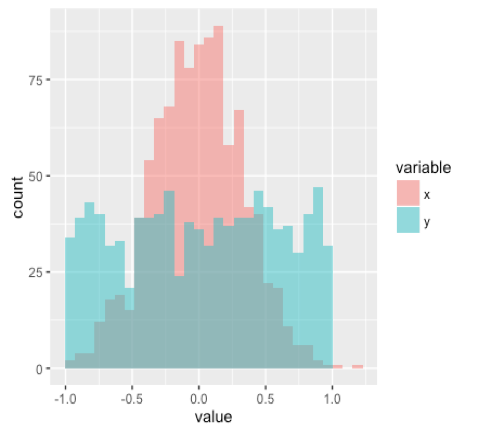
X \sim \mathcal{N}(0,1/3), \ \ Y \sim U(-1,1)
これはどちらも平均$0$,分散$1/3$となる場合です.ヒストグラムを描くと
のようになり明らかに$P\neq Q$です.
しかし,同様にt-検定とF-検定を行うと
Two Sample t-test
data: x and y
t = -0.28689, df = 198, p-value = 0.7745
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.1823799 0.1360547
sample estimates:
mean of x mean of y
0.03289270 0.05605532
F test to compare two variances
data: x and y
F = 0.69655, num df = 99, denom df = 99, p-value = 0.07351
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.4686646 1.0352290
sample estimates:
ratio of variances
0.6965452
やはり平均(1次モーメント)や分散(2次モーメントまで)しかみていないので,どちらもp値は$0.05$以上で帰無仮説は棄却されず分布の違いを検出することができません.
そこで事前に確率分布を仮定しないノンパラメトリックな方法が必要になってきます.
雑記)t-検定をウェルチの検定で行うか判断するために先に分散の検定を行う人がいますがやめましょう.検定を繰り返すと各々の検定は有意水準$\alpha$でも,全体としてType 1 error率は$\alpha$より大きくなってしまいます(つまり帰無仮説が正しいのに棄却してしまいがちになります).なので,多重比較では有意水準をコントロールする補正(ボンフェローニ補正など)を考えなくてはなりません.
ノンパラメトリックな手法(古典的方法)
様々の方法が提案されていますが,2標本問題でスタンダードな方法と考えられる2つの検定を紹介します.
コルモゴロフ-スミノフ検定
コルモゴロフ-スミノフ検定は検定統計量として
D_N = \sup_{t\in \mathbb{R}}\left |F_N^1(t)-F_N^2(t)\right|
を用います.ただし
F_N(t) = \frac{1}{N}\sum_{i=1}^N I(X_i \leq t)
です.これは次の図を見ると理解しやすいです.
それぞれの母集団の経験分布を計算して,その差が最も大きくなるところを検定統計量としているわけです.
こちらもそれぞれの1次元データをx,yに渡して
# コルモゴロフ-スミノフ検定
ks.test(x,y)
とすれば簡単に実行できます.
Mann-WhitneyのU検定(Wilcoxonの順位和検定)
マンホイットニーのU検定はその名の通りU統計量と呼ばれるクラスの統計量を利用した検定になっています.そのあたりの話は,「はじめに」のリンク先の資料に記載しています.
Wilcoxonの順位和検定と呼ばれるもの(こちらはランク統計量の考え方で導かれる)と同等です.Rの関数はwilcoxon.testとなっています.
2変数関数 $h(x,y)=1[x \leq y]$ を考えます(カーネルといいます.カーネル法とは関係ないです).ただし$1[\cdot]$は中身が成立するときのみ$1$となりその他は$0$となる指示関数です.帰無仮説$P=Q$の元で,
\mathbb{E}[h(X,Y)] = \mathbb{P}(X\leq Y) = \frac{1}{2} (:= \theta)
となります.
ここでU統計量を
U_{\ell,n} = \frac{1}{\ell n}\sum_{i, j}1[X_i\leq Y_j]
と定義します.これがMann-WhitneyのU検定の検定統計量です.意味合いとしては,$X$と$Y$の2つの対を考えて,$Y$の方が大きかった回数を数えて,組み合わせの総数で割っていることになります.
帰無仮説が真(同分布)であれば,この値は$\theta =1/2$に近い値をとることになるでしょう.こうして上の統計量で2標本検定が可能となるわけです.
考察として$P\neq Q$だったとしても,中央値が同じで中央値まわりで対称なケース,つまり先ほどの
X \sim \mathcal{N}(0,1/3), \ \ Y \sim U(-1,1)
なんかは識別できなさそうです.実際,
x <- rnorm(1000,0,sd=sqrt(1/3))
y <- runif(1000,-1,1)
# Mann-WhitneyのU検定(Wilcoxonの順位和検定)
wilcox.test(x,y)
Wilcoxon rank sum test with continuity correction
data: x and y
W = 492340, p-value = 0.5528
alternative hypothesis: true location shift is not equal to 0
かなりサンプルサイズを大きくとりましたが,やはり検出できません.
注)統計量を作っただけでは仮説検定は行えません.統計量の従う分布が分からなければ棄却域(p値)は計算できないからです.実はU統計量はその漸近分布の性質が一般論でかなり研究されていて,
\sqrt{N}(U_{\ell,n} - \theta)
が漸近的に(サンプル数を大きくした時に)正規分布に従うことが分かっています.統計の入門書で仮説検定を勉強されたことのある方なら,Z検定などでテキストの巻末の正規分布表とにらめっこしながら,棄却できるか計算した経験がおありですよね?あんな感じで上式の値を検定統計量として棄却域と比較すればいいのです.
多少詳しくは「はじめに」のスライド,本当に詳しくは参考文献のvan der vaartなんかを参照してください.
結局何がいいの?
ノンパラメトリック検定をいくつか紹介してきましたが,決定打となるような手法はなかなか見つかりません.そもそも1次元ならヒストグラムを書いたら分かるじゃないか!って気分にもなってきました.視覚化できないような高次元の確率分布だって考えてみたいものです.ここからがカーネル法の出番です!でも,SVMなんかで使われているカーネル法をどうこの問題に当てはめたらいいのか自明ではありません.
そこで,近年のカーネル法でのホットトピックであるカーネル平均(Kernel mean embedding)の出番です!
正定値カーネルによる2標本検定
特徴写像の確率測度への拡張
以下では,$k$で特性的な正定値カーネル(ガウシアンカーネル${k(x, x') = exp(-\frac {||x - x'||^2} {2\sigma^2} )}$だと思っておいてもらえば問題ないです),$\mathcal{H}$で正定値カーネル$k$により定義される再生核ヒルベルト空間を表すとします.
確率測度$\mathbb{P}$のカーネル平均は
m_P^k := \int k(\cdot,x)d\mathbb{P}(x)
と定義されます(積分はバナッハ空間(ヒルベルト空間はバナッハ空間)に値をとる関数へのルベーグ積分の一般化であるボホナー積分.今回の話ではそんなこと気にしなくてもまったく問題ないですが,気になる人がいそうなので念のため).
Kernel mean embeddingはカーネル法の特徴写像の確率測度への拡張となっています.
統数研の福水先生やマックスプランク研究所のB.Schölkopf先生,UCLのA. Gretton先生らをはじめとし,多くの方々により研究され発展してきています.先日のNIPSのproceedingsにもKernel mean embedding周りの論文は何本かあがっていましたね.年末の時間があるときにでもチェックしておきたいものです.
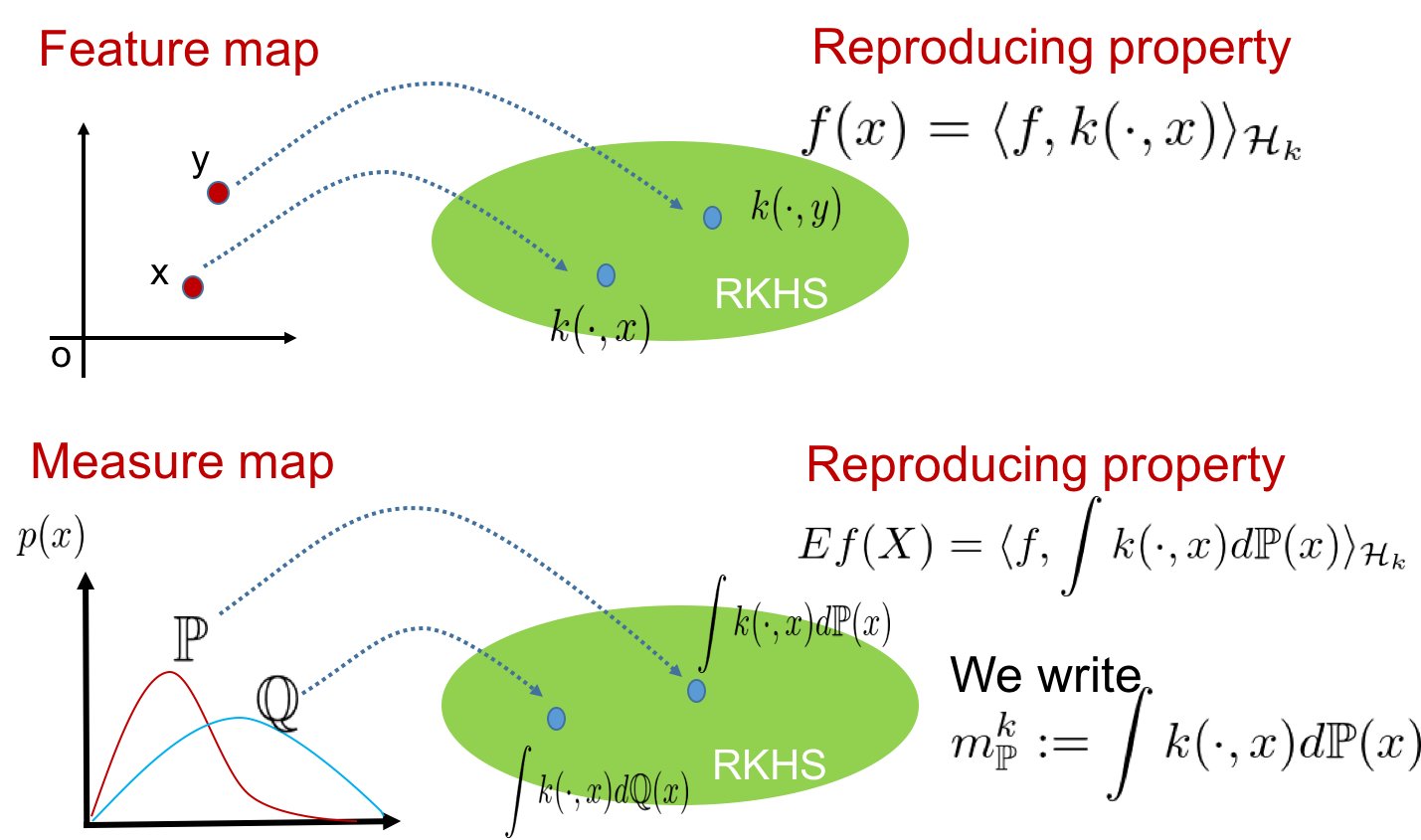
従来のカーネル法と対応させた概念図は以下のようになっています.
もとの確率測度として,ディラック測度を考えれば,カーネル平均は特徴写像と一致します;
\int k(\cdot,y) \delta_x(y) = k(\cdot,x).
詳細は参考文献にある福水先生のカーネル法入門,無料で読めるものでしたらarXivにあがっているK.Muandet先生のサーベイ論文『Kernel Mean Embedding of Distributions: A Review and Beyonds』などを参照してください.
なぜKernel mean embedding?
なぜ2標本問題のノンパラ化にカーネルを使うとうまくいくと考えられるのでしょうか?それは,ガウシアンカーネルなどの特性的と呼ばれるクラスのカーネルにより定義されたカーネル平均は,もとの確率分布のすべてのモーメントの情報を保持しているからです.
実際,カーネル関数として$k(x,x')=e^{xx'}$などとして,$X \sim P$としたとき$P$のカーネル平均は
m_k^P(t) = \mathbb{E}_{X\sim P}[k(t,X)]=\int e^{tx}dP(x)\\
=\int 1+tx+\frac{t^2x^2}{2}+\frac{t^3x^3}{3!}+\cdots dP(x)\\
=1+t\mathbb{E}_{X\sim P}[X]+\frac{t^2}{2}\mathbb{E}_{X\sim P}[X^2]+\frac{t^3}{3!}\mathbb{E}_{X\sim P}[X^3]+\cdots
となり,$P$の全てのモーメントの情報が保持されていることが確認できます.どうやらKernel mean embeddingを利用すれば理想的な検定方式が作れそうです.
さらにカーネル法は正定値カーネルさえ定義できれば,多次元データはもちろん文字列やグラフといった構造化データなどに対しても同じ方法論が適用できるのでした.つまり正定値カーネルを定義すればどんなデータにでも仮説検定を行うことができるのです!スゴイ!!
カーネル2標本検定の検定方式
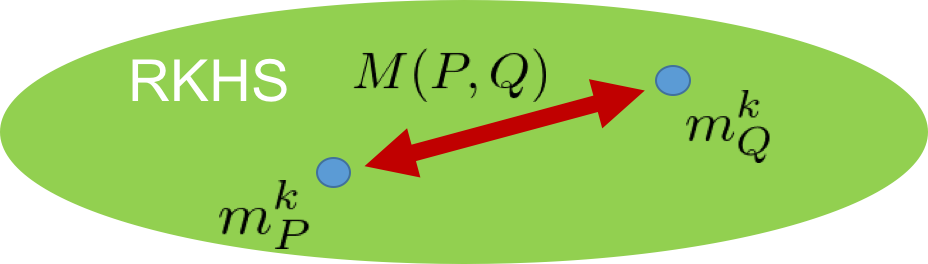
再生核ヒルベルト空間での分布$P$と$Q$のカーネル平均の距離を考えます.これはMaximum mean discrepancy(MMD)と呼ばれます.
定義式はこうです.
M^2(P,Q) :=||m_P^k-m_Q^k||_{\mathcal{H}}^2
$P=Q$なら$M^2(P,Q)=0$となります.これの推定量が検定に利用する統計量となります.推定量の計算は簡単でカーネル平均を推定量$\hat{m}_P^k=\frac{1}{\ell}\sum k(\cdot,X_i)$で置き換えるだけです.ここからは,いつもの(?)カーネル法です.
\hat{M}_{\ell,n}=||\hat{m}_P-\hat{m}_Q||_{\mathcal{H}}^2 =\\
\frac{1}{\ell^2}\sum_{a,b=1}^{\ell}k(X_a,X_b)+ \frac{1}{n^2}\sum_{c,d=1}^{n}k(Y_c,Y_d)-\frac{2}{\ell n}\sum_{a=1}^{\ell}\sum_{c=1}^nk(X_a,Y_c)
と計算できます.実際にプログラムで計算するのも簡単で,例えばKernelabパッケージを使って,
library(kernlab)
X <- rnorm(100,0,1)
Y <- rnorm(100,0,1)
X <- as.matrix(X)
Y <- as.matrix(Y)
s <- sigest(rbind(X,Y),scaled=FALSE)[2]
rbf <- rbfdot(sigma = s)
nX <- dim(X)[1]
nY <- dim(Y)[1]
N <- nX+nY
Kx <- kernelMatrix(x = X,kernel = rbf)
Ky <- kernelMatrix(x = Y,kernel = rbf)
# get MMD estimator
term1 <- sum(Kx)/(nX^2)
term2 <- sum(Ky)/(nY^2)
term3 <- 2*sum(kernelMatrix(x=X,y=Y,kernel=rbf))/(nX*nY)
MMDestimator <- term1+term2-term3
MMDestimator
などとすればいいと思います.グラム行列を作って全成分を足してるだけですね.上の場合XとYどちらも標準正規分布としていて,MMDの推定量の値は0.01988となってやはり0に近い値となっています.
しかし,定義から分かるように,この推定量は常に0以上の値をとります.しかし帰無仮説$P=Q$のもとでMMDは0となるのでした.これは上の推定量が不偏でない,つまり偏りがあることを意味しています.不偏となるように次のように統計量を修正します.
U_{\ell,n}=\frac{1}{\ell (\ell-1)}\sum_{a\neq b}k(X_a,X_b)+\frac{1}{n(n-1)}\sum_{c\neq d}k(Y_c,Y_d)-\frac{2}{\ell n}\sum_{a=1}^{\ell}\sum_{c=1}^nk(X_a,Y_c)
Rのコードも対応して変更します.
library(kernlab)
X <- rnorm(100,0,1)
Y <- rnorm(100,0,1)
X <- as.matrix(X)
Y <- as.matrix(Y)
s <- sigest(rbind(X,Y),scaled=FALSE)[2]
rbf <- rbfdot(sigma = s)
nX <- dim(X)[1]
nY <- dim(Y)[1]
N <- nX+nY
Kx <- kernelMatrix(x = X,kernel = rbf)
Ky <- kernelMatrix(x = Y,kernel = rbf)
# get unbiased MMD estimator
diag(Kx)<-0;diag(Ky)<-0
term1 <- sum(Kx)/(nX*(nX-1))
term2 <- sum(Ky)/(nY*(nY-1))
term3 <- 2*sum(kernelMatrix(x=X,y=Y,kernel=rbf))/(nX*nY)
Ustatistic <- term1+term2-term3
Ustatistic
和をとる前にXとYのグラム行列の対角成分を0として,割る値を修正しました.実際推定量の値は-0.00436で負の値となりましたが先ほどよりも0に近い値になりました.
棄却域をどう作るか
統計量$U_{\ell,n}$を作ることができました.しかし,カーネルも入っていてどんな分布に従うのか分かりそうにもありません.
しかし,Mann-WhitneyのU統計量のときと同じ記号を使っていたことから気づかれたかもしれまんせんが,実はこれもU統計量になっています.対応する$h$は
h(x_1,x_2;,y_1,y_2)=k(x_1,x_2)+k(y_1,y_2)
-\frac{1}{2}[k(x_1,y_1)+k(x_1,y_2)+k(x_2,y_1)+k(x_2,y_2)]
です.
つまり,U統計量の一般論を当てはめて帰無仮説のもとでの漸近分布を求め,棄却域を決定することができるのです!
結果を述べると次のような定理が得られます.
$\frac{\ell}{N}\rightarrow \gamma,\frac{n}{N}\rightarrow 1-\gamma$を仮定する.このとき帰無仮説$P=Q$のもとで
N U_{\ell,n} \stackrel{{d}}\rightarrow \sum_{i=1}^{\infty}\lambda_i \left(Z_i^2 - \frac{1}{\gamma (1-\gamma)}\right) \\
\mbox{where } Z_i \stackrel{{i.i.d}}\sim \mathcal{N}\left( 0,\frac{1}{\gamma(1-\gamma)}\right).
$(\lambda_i)_{i=1}^{\infty}$がなにものかという話は一旦置いておきます.
お気づきの方もおられるでしょうが,先ほどは$U_{\ell,n}$に掛けていたのが$\sqrt{N}$だったのに今回は$N$であること,さらに$\theta$を引いていないことに注目しましょう.まず$\theta$を引いていないのは帰無仮説のもとでMMDは0で$U_{\ell,n}$がその不偏推定量になっているためです(Mann-Whitneyでは$1/2$でした).
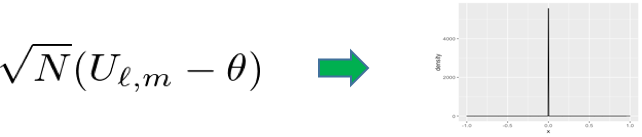
$\sqrt{N}$でない理由は,このU統計量が縮退した(degenerateな)U統計量であるためです.$\sqrt{N}$倍だと漸近分布の分散が0になってしましい,下の図のように1点分布になってしまうのです.
そこで,$\sqrt{N}$より大きなオーダーを掛けて,漸近分布に広がりをもたせてやる必要があるわけです.degenerateなU統計量の一般論はかなり難しいのですが,参考文献のvan der Vaartの本には詳しく載っているので興味のある方は参照してください.今回のケースの証明は福水先生のカーネル法入門にも載っています.
次に$(\lambda_i)_{i=1}^{\infty}$がなにものかという話をします.多少,関数解析の知識がないと以下の説明は厳しいと思うので,苦手な人は推定のステップまで読み飛ばしてください.
$(\lambda_i)_{i=1}^{\infty}$は,カーネル関数を$\tilde{k}(x,y) = k(x,y) - \mathbb{E}[k(x,X)]-\mathbb{E}[k(X,y)]+E[k(X,\tilde{X})]$ (ただし,$X,\tilde{X}\stackrel{{i.i.d}}\sim P$)としたときの$L^2(P)$空間上の積分作用素の非ゼロ固有値です.つまり,
\int \tilde{k}(x,y)\phi_i(y)dP(y)=\lambda_i\phi_i(x)
を満たす非負実数値です.
これをサンプルから推定する方法は,考案者であるGretton先生の論文で紹介されています.比較的単純で$\tilde{k}$をもとにしたサンプルXのグラム行列を作り,その非ゼロ固有値を計算します.それをXのサンプル数で割ったものが$\lambda_i$の一致推定量となります.
このグラム行列は中心化グラム行列と呼ばれて次のような綺麗な形でかけます.
\tilde{K}_{ij} = k(X_i,X_j) - \frac{1}{N}\sum_{b=1}^Nk(X_i,X_b) - \frac{1}{N}\sum_{a=1}^Nk(X_a,X_j)+ \frac{1}{N^2}\sum_{a,b=1}^Nk(X_a,X_b)= (Q_N KQ_N)_{ij}. \\ \mbox{where. } Q_N = I_N - \frac{1}{N}1_N1_N^T
$I_N$は$N\times N$単位行列,$1_N$は全ての成分が1の$N$次元ベクトルです.
先のコードの続きで,以下のようにすれば$(\lambda_i)_{i=1}^{\infty}$の推定量が得られます.
one <- matrix(1,nX,1)
H <- diag(nX) - 1/nX*(one%*%t(one))
K <- kernelMatrix(x = X,kernel = rbf)
centerd_K <- H%*%K%*%H
lambda <- 1/nX*eigen(centerd_K)$values
lambda_pos <- lambda[lambda>0.001]
Rではexactに0にはならないので,0.001以下の値は0とみなすようにしました.実際グラム行列の固有値はかなり早く縮退してほとんどの固有値が0になります.
これでようやく棄却域を求める準備が整いました.漸近分布はそれでも複雑な形(非心のカイ二乗分布っぽい何かでしょうか?)サンプリングで推定することにしましょう.
漸近分布$\sum_{i=1}^{\infty}\lambda_i \left(Z_i^2 - \frac{1}{\gamma (1-\gamma)}\right)$からサンプリングする関数を次のように定義します.
rnull <- function(lambda,size,gamma){
kekka <- rep(0,size)
for(i in 1:size){
z <- rnorm(length(lambda),mean=0,sd=sqrt(1/(gamma*(1-gamma))))
kekka[i] <- sum(lambda*(z^2-1/(gamma*(1-gamma))))
}
return(kekka)
}
lambdaに推定した固有値,sizeにサンプリングしたい個数,gammaにXの割合を与えてやれば,上の分布からのサンプルを返してくれます.
これを使って,有意水準0.05で棄却域を推定するには以下のようにします.
null_sample <- rnull(lambda=lambda_pos,size=1000,gamma=nX/N)
critical_value <- sort(null_sample)[0.95*length(null_sample)]
サンプルをソートして上側5%点を計算しているだけです.sizeに指定する値は大きければ大きい方がよいです.
あとは,これを先に求めた$NU_{\ell,n}$の値と比較して,$NU_{\ell,n}$の方が大きければ$P=Q$を棄却して$P\neq Q$,小さければ$P=Q$を棄却できない,というふうにすれば有意水準0.05の2標本検定の完成です.
実演
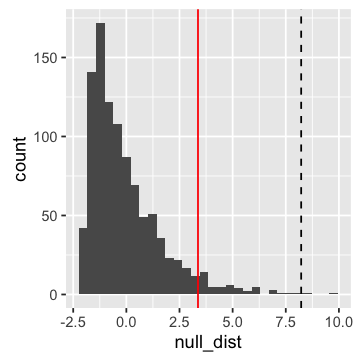
全て関数化して,先ほどのサンプルに対して検定してみましょう.ついでに推定された漸近分布(ヒストグラム)と検定統計量(statistic,破線),棄却域(CriticalValue,赤線)をプロットしてみました.(githubに載せています)
x <- rnorm(500,0,sd=sqrt(1/3))
y <- runif(500,-1,1)
kernelTST(x,y)
$CriticalValue
[1] 3.37031
$TestStatistic
[1] 8.224383
$NullHypothesis
[1] "Rejected"
ちゃんと検出することができました.
せっかくカーネル化したのだから,多変量データに対しても2標本検定を行ってみましょう.簡単にMNISTデータ(手書き数字データ)で各数字ごとに確率分布は異なるのか(同じ分布なら確率分布は同じなのか)カーネル2標本検定を行ってみました.MNISTデータはkaggleのものです.
なんとなく見分けにくそうに見えた(?)7と9をそれぞれ2000個ずつサンプルをとって検定してみます.
library(dplyr)
library(data.table)
library(ggplot2)
library(kernlab)
dt <- tbl_df(fread("train.csv"))
dt_7 <- filter(dt,label==7)[,-1]
dt_9 <- filter(dt,label==9)[,-1]
dt_7_1 <- dt_7[1:2000,]
dt_7_2 <- dt_7[2001:4000,]
dt_9_1 <- dt_9[1:2000,]
dt_9_2 <- dt_9[2001:2000,]
kernelTST(dt_7_1,dt_9_1)
$CriticalValue
[1] 1.007231
$TestStatistic
[1] 372.1564
$NullHypothesis
[1] "Rejected"
ちゃんと棄却されました.同じ文字だとどうなるかも試してみます.
kernelTST(dt_7_1,dt_7_2)
kernelTST(dt_9_1,dt_9_2)
# 7vs7
$CriticalValue
[1] 0.9227437
$TestStatistic
[1] 0.9032882
$NullHypothesis
[1] "Accepted"
# 9vs9
$CriticalValue
[1] 0.9944741
$TestStatistic
[1] -183.6595
$NullHypothesis
[1] "Accepted"
期待通り棄却されませんでした.実際は事前にPCAなんかをかけた方がいい気もするのですが,上手くいったのでこれでよしとします.
検出力やType 1 errorの手法ごとの比較も重要なのですが,それは「はじめに」のスライドに載せているのでそちらを参照してください.
参考文献
- A. Gretton, et al. A fast, consistent kernel two-sample test. Advances in neural information processing systems (2009).
- A. Gretton, et al. A kernel two-sample test. Journal of Machine Learning Research 13: 723-773. (2012).
- 福水健次. カーネル法入門—正定値カーネルによるデータ解析. 朝倉 書店, (2010).
- K. Muandet, et al. Kernel Mean Embedding of Distributions: A Review and Beyonds. arXiv:1605.09522 (2016).
- A. W. Van der Vaart. Asymptotic statistics. Cambridge series in statistical and probabilistic mathematics. (2000).
あとがき
かなり基本的な手法から始まり,カーネル2標本検定まで紹介しました.私自身勉強中の身ですので,間違い,誤解,プログラムミス等あるかもしれません.気づかれた方はコメント等いただけると幸いです.