Go to Qiita Advent Calendar 2024 Top
LoginSignup
1
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@ytaki0801(Yozo TAKIZAWA)

ラムダ式プログラミング一時間体験講座（Python/Ruby/JavaScript同時並行版）

Last updated at Posted at 2021-07-24

筆者『一時間体験講座』第４弾（１，２，３）．内容的にはこちらの方が近いかもしれませんが，より実践的な内容となっています．複数言語対応の体験ということもあって，用語や仕組みの正確なところの解説はほとんどありません1．

前書き

この記事は，ともすれば難読化扱いされかねないラムダ式を用いたプログラミングの普及の一助になればという筆者の被害妄想想いから生まれました．３言語同時並行で進めますが，いずれの言語も事前知識はあまり必要ありません．講座の目標として，次の記述が何を行うものかわかるようになればいいなあという感じです．

Python
$ python
>>> (lambda u: u(u))(lambda u: lambda n,a,b: a if n == 0 else u(u)(n - 1, b, a + b))(40,0,1)
102334155
>>> exit()
$
Ruby
$ irb --simple-prompt
>> ->u{u[u]}[->u{->n,a,b{n == 0 ? a : u[u][n-1,b,a+b]}}][40,0,1]
=> 102334155
>> exit
$
JavaScript
$ node
> (u=>u(u))(u=>(n,a,b)=> n == 0 ? a : u(u)(n-1,b,a+b))(40,0,1)
102334155
> （Ctrlキーを押しながらD）
$

実行例はいずれも，UNIXシェルからの対話モード（REPL）で記載しています．それぞれの環境で適宜読み替えてもらえればと思います．

※JavaScriptについては，上記Node.jsの他，Chrome/EdgeでCtrl+Shift+Jで呼び出されるconsoleでも実行可能です．
chconsole

ラムダ式の基本

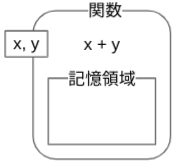
ラムダ式は無名関数とも呼ばれ，名前のない関数です．関数そのものは数学のそれと基本的には同じで，ある変数に依存して決まる値あるいはその対応を表す式によって構成されています．プログラミングでは，変数やその変数の値を引数（ひきすう）と呼んでいます．次の図は，関数処理の大まかな流れです．

引数として変数$x$，$y$をとってその変数の値を足した結果を返すラムダ式は，次のように記述できます．

Python
>>> lambda x, y: x + y
Ruby
>> ->x,y{x+y}
JavaScript
> (x,y)=>x+y

上記を実行2しただけでは『関数だよ』という結果表示しかありません．ですが，ラムダ式はこの実行時に，変数と値の対応を保持するための記憶領域を内部に作ります3．

closure
変数に値を対応させて処理を行わせる4には，実際の値を引数として指定します．

Python
>>> (lambda x, y: x + y)(10, 20)
30
Ruby
>> ->x,y{x+y}[10,20]
=> 30
JavaScript
> ((x,y)=>x+y)(10,20)
30
Python
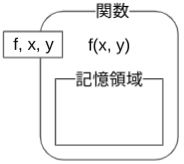
>>> lambda f, x, y: f(x, y)
Ruby
>> ->f,x,y{f[x,y]}
JavaScript
> (f,x,y)=>f(x,y)
Python
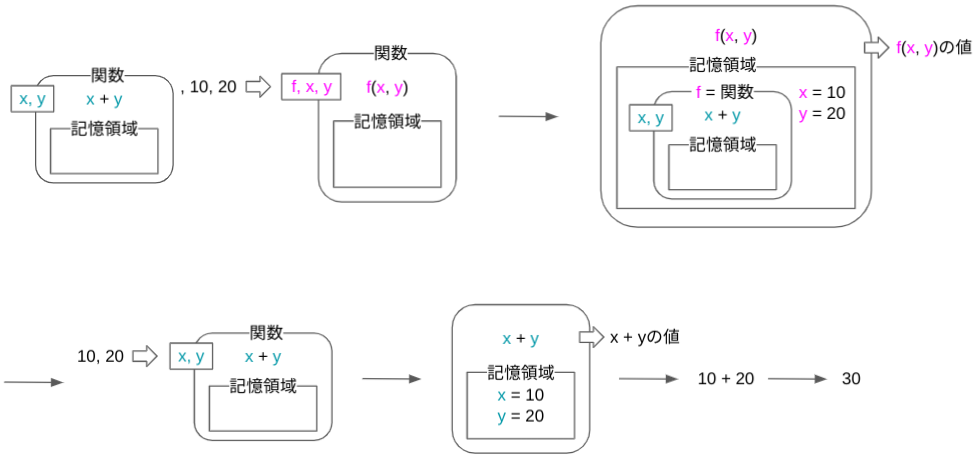
>>> (lambda f, x, y: f(x, y))(lambda x, y: x + y, 10, 20)
30
Ruby
>> ->f,x,y{f[x,y]}[->(x,y){x+y},10,20]
=> 30
JavaScript
> ((f,x,y)=>f(x,y))((x,y)=>x+y,10,20)
30
Python
>>> lambda x: lambda y: x + y
Ruby
>> ->x{->y{x+y}}
JavaScript
> x=>y=>x+y
Python
>>> (lambda x: lambda y: x + y)(10)
Ruby
>> ->x{->y{x+y}}[10]
JavaScript
> (x=>y=>x+y)(10)

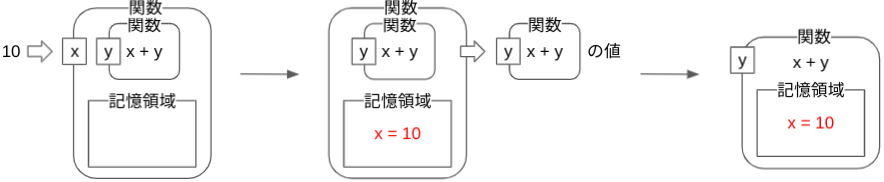
lambda-closure4
このラムダ式に値20を指定すると，引数$y$に20が対応付けられ，なおかつ，$x+y$が計算されますから，晴れて$10+20⇒30$が表示されます．

Python
>>> (lambda x: lambda y: x + y)(10)(20)
30
Ruby
>> ->x{->y{x+y}}[10][20]
=> 30
JavaScript
> (x=>y=>x+y)(10)(20)
30

eval-apply3

ループ式と条件分岐

次は，ループを発生させるラムダ式です．

Python
>>> (lambda u: u(u))(lambda u: u(u))
Ruby
>> ->u{u[u]}[->u{u[u]}]
JavaScript
> (u=>u(u))(u=>u(u))

今回取り上げているプログラミング言語の処理系は，一定回数以上のループ（正確には，再帰）が発生するとエラーとなり停止します．

Python
>>> (lambda u: u(u))(lambda u: u(u))
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 1, in <lambda>
  File "<stdin>", line 1, in <lambda>
  File "<stdin>", line 1, in <lambda>
  [Previous line repeated 996 more times]
RecursionError: maximum recursion depth exceeded
Ruby
>> ->u{u[u]}[->u{u[u]}]
Traceback (most recent call last):
       16: from (irb):1:in `block in irb_binding'
       15: from (irb):1:in `block in irb_binding'
       14: from (irb):1:in `block in irb_binding'
       13: from (irb):1:in `block in irb_binding'
       12: from (irb):1:in `block in irb_binding'
       11: from (irb):1:in `block in irb_binding'
       10: from (irb):1:in `block in irb_binding'
        9: from (irb):1:in `block in irb_binding'
        8: from (irb):1:in `block in irb_binding'
        7: from (irb):1:in `block in irb_binding'
        6: from (irb):1:in `block in irb_binding'
        5: from (irb):1:in `block in irb_binding'
        4: from (irb):1:in `block in irb_binding'
        3: from (irb):1:in `block in irb_binding'
        2: from (irb):1:in `block in irb_binding'
        1: from (irb):1:in `block in irb_binding'
SystemStackError (stack level too deep)
JavaScript
> (u=>u(u))(u=>u(u))
Thrown:
RangeError: Maximum call stack size exceeded
    at u (repl:1:11)
    at u (repl:1:14)
    at u (repl:1:14)
    at u (repl:1:14)
    at u (repl:1:14)
    at u (repl:1:14)
    at u (repl:1:14)
    at u (repl:1:14)
    at u (repl:1:14)
    at u (repl:1:14)

なぜ，ループが発生するのでしょうか？それは，上記の式が，引数に値として同じラムダ式を指定することで，全く同じ式が構成されるからです．構成された式は再び引数に同じラムダ式を指定していますから，引数への値の指定が次々と行われます．

Python
(lambda u: u(u))(lambda u: u(u))
➡ u(u)  ※ラムダ式の記憶領域に『u = lambda u: u(u)』を保持
➡ (lambda u: u(u))(lambda u: u(u))
➡ u(u)  ※ラムダ式の記憶領域に『u = lambda u: u(u)』を保持
➡ (lambda u: u(u))(lambda u: u(u))
➡ …
Ruby
->u{u[u]}[->u{u[u]}]
➡ u[u]  ※ラムダ式の記憶領域に『u = ->u{u[u]}』を保持
➡ ->u{u[u]}[->u{u[u]}]
➡ u[u]  ※ラムダ式の記憶領域に『u = ->u{u[u]}』を保持
➡ ->u{u[u]}[->u{u[u]}]
➡ …
JavaScript
(u=>u(u))(u=>u(u))
➡ u(u)  ※ラムダ式の記憶領域に『u = u=>u(u)』を保持
➡ (u=>u(u))(u=>u(u))
➡ u(u)  ※ラムダ式の記憶領域に『u = u=>u(u)』を保持
➡ (u=>u(u))(u=>u(u))
➡ …

このループ式の意味するところは，適切な脱出方法があれば，繰り返し相当の処理をラムダ式のみで記述できることです．ここでは，値として指定している（右側の）ラムダ式の中に，『繰り返すたびに値が変化する変数』と『その値によって条件分岐する仕組み』もつラムダ式を組み込んでみましょう．

次は，

  • 繰り返すたびに値が変化する変数として$n,r$のふたつをもつ
  • $n$は繰り返すたびに$n-1$に置き換わり，$r$は繰り返すたびに$n*r$に置き換わる
  • $n$が$1$より小さくなれば$r$を返して終了する

というラムダ式を組み込んだ例です．結果として階乗計算を行うプログラムとなり，$n,r$それぞれの初期値として$5,1$という引数を指定して実行しています．

Python
>>> (lambda u: u(u))(lambda u: (lambda n,r: r if n < 1 else u(u)(n - 1, n * r)))(5, 1)
120
Ruby
>> ->u{u[u]}[->u{->n,r{n < 1 ? r : u[u][n-1,n*r]}}][5,1]
=> 120
JavaScript
> (u=>u(u))(u=>(n,r)=>n < 1 ? r : u(u)(n-1,n*r))(5,1)
120

階乗計算については，単純に，$n$を$1$ずつ減らしながら$n$の値を掛けていくループの形でも実現できます．この場合，階乗計算は$n!=n×(n-1)!=n×(n-1)×(n-2)!=…$というように，実際の掛け算を後回しにするスタイル9で行われます．

Python
>>> (lambda u: u(u))(lambda u: (lambda n: 1 if n < 1 else n * u(u)(n - 1)))(5)
120
Ruby
>> ->u{u[u]}[->u{->n{n < 1 ? 1 : n * u[u][n-1]}}][5]
=> 120
JavaScript
> (u=>u(u))(u=>n=>n < 1 ? 1 : n * u(u)(n-1))(5)
120

プログラムコード例

ラムダ式によるプログラミングは，基本的には，判断分岐に三項演算子，反復処理に前章の表現10を用いることで，様々なアルゴリズムを記述することができます．ただし，ラムダ式の性質上，多くの場合，引数を入力として戻り値を出力とするプログラミングスタイル11とする必要があります．

フィボナッチ数列

冒頭の記述例は40番目のフィボナッチ数を求めるラムダ式の例ですが，0番目からn番目までのフィボナッチ数列を求めたい場合は，別途用意した変数を用いて，途中経過の値を追加した配列等に置き換えていき，最後にその変数の値を返すことで得られます．

Python
>>> (lambda u: u(u))(lambda u: lambda n,a,b,r: r if n < 0 else u(u)(n - 1, b, a + b, r + [a]))(10,0,1,[])
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
Ruby
>> ->u{u[u]}[->u{->n,a,b,r{n < 0 ? r : u[u][n-1,b,a+b,r+[a]]}}][10,0,1,[]]
=> [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
JavaScript
> (u=>u(u))(u=>(n,a,b,r)=>n < 0 ? r : u(u)(n-1,b,a+b,r.concat(a)))(10,0,1,[])
[ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ]

FizzBuzz

一行で表現することもできますが，コードの見やすさのため，適宜改行や字下げを行う方が良いかもしれません．この時，ラムダ式として完結する部分の直後に改行すると，引数として値を指定する前にラムダ式単体で実行されてしまうことに注意して下さい．

Python
>>> (lambda u: u(u))(
...  lambda u:
...    lambda n,r:
...      r if n < 1 else
...      u(u)(n-1, ["FizzBuzz"] + r) if n%15==0 else
...      u(u)(n-1, ["Fizz"] + r)     if n%3==0  else
...      u(u)(n-1, ["Buzz"] + r)     if n%5==0  else
...      u(u)(n-1, [n] + r)
... )(30,[])
[1, 2, 'Fizz', 4, 'Buzz', 'Fizz', 7, 8, 'Fizz', 'Buzz', 11, 'Fizz', 13, 14, 'FizzBuzz', 16, 17, 'Fizz', 19, 'Buzz', 'Fizz', 22, 23, 'Fizz', 'Buzz', 26, 'Fizz', 28, 29, 'FizzBuzz']
Ruby
>> ->u{u[u]}[->u{->n,r{
?>   n<1 ? r :
?>   n%15==0 ? u[u][n-1,["FizzBuzz"]+r] :
?>   n%3==0  ? u[u][n-1,["Fizz"]+r] :
?>   n%5==0  ? u[u][n-1,["Buzz"]+r] :
?>   u[u][n-1,[n]+r]}}
>> ][30,[]]
=> [1, 2, "Fizz", 4, "Buzz", "Fizz", 7, 8, "Fizz", "Buzz", 11, "Fizz", 13, 14, "FizzBuzz", 16, 17, "Fizz", 19, "Buzz", "Fizz", 22, 23, "Fizz", "Buzz", 26, "Fizz", 28, 29, "FizzBuzz"]
>>
JavaScript
> (u=>u(u))(u=>(n,r)=>
... n==1 ? n+r :
... n%15==0 ? u(u)(n-1," FizzBuzz"+r) :
... n%3==0  ? u(u)(n-1," Fizz"+r) :
... n%5==0  ? u(u)(n-1," Buzz"+r) :
... u(u)(n-1," "+n+r)
... )(30,"")
'1 2 Fizz 4 Buzz Fizz 7 8 Fizz Buzz 11 Fizz 13 14 FizzBuzz 16 17 Fizz 19 Buzz Fizz 22 23 Fizz Buzz 26 Fizz 28 29 FizzBuzz'

コラッツ数列

3n+1問題とも呼ばれるコラッツの問題において，正の整数を初期値として$n$に与えた際に，次の操作によって$1$まで到達する間に求められる値の列を指します．

  • $n$が偶数の時，$n$を$2$で割る
  • $n$が奇数の時，$n$に$3$を掛けて$1$を足す

下記の例では，初期値が$27$の時の数列を求めています．

Python
>>> (lambda u:u(u))(lambda u: lambda n,r: r+[int(n)] if n==1 else u(u)(n/2,r+[int(n)]) if n%2==0 else u(u)(n*3+1,r+[int(n)]))(27,[])
[27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]
Ruby
>> ->u{u[u]}[->u{->n,r{n==1?r+[n]:n%2==0?u[u][n/2,r+[n]]:u[u][n*3+1,r+[n]]}}][27,[]]
=> [27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]
JavaScript
> (u=>u(u))(u=>(n,r)=>n==1?r+n:n%2==0?u(u)(n/2,r+n+" "):u(u)(n*3+1,r+n+" "))(27,"")
'27 82 41 124 62 31 94 47 142 71 214 107 322 161 484 242 121 364 182 91 274 137 412 206 103 310 155 466 233 700 350 175 526 263 790 395 1186 593 1780 890 445 1336 668 334 167 502 251 754 377 1132 566 283 850 425 1276 638 319 958 479 1438 719 2158 1079 3238 1619 4858 2429 7288 3644 1822 911 2734 1367 4102 2051 6154 3077 9232 4616 2308 1154 577 1732 866 433 1300 650 325 976 488 244 122 61 184 92 46 23 70 35 106 53 160 80 40 20 10 5 16 8 4 2 1'

備考

記事に関する補足

  • 説明はするけど対応する用語は出さないという…．あとで用語一覧を追加するかも．→脚注にしてみました．

更新履歴

  • 2021-08-10：ループ式と条件分岐の章を大幅削減，プログラムコード例の追加
  • 2021-07-25：用語の類を脚注に記載
  • 2021-07-24：初版公開

  1. 用語の類は脚注にしました． ↩

  2. 評価（eval） ↩

  3. クロージャ ↩

  4. 関数適用（apply）
    eval/apply
    実際の値については，ラムダ式を指定5することもできます．次は，３つの引数$f$，$x$，$y$をとり，$f(x,y)$，すなわち，関数$f$に$x$，$y$の値を渡して計算させるラムダ式です． ↩

  5. 高階関数（引数が関数）
    lambda-closure2
    $f$に上記の足し算を行うラムダ式を，$x$，$y$にそれぞれ10，20を引数として指定して実行すると，足し算のラムダ式の時と同じ結果が得られます6． ↩

  6. ラムダ計算のβ簡約相当
    注意してほしいのは，$f$，$x$，$y$のラムダ式の$x$，$y$と，足し算を行うラムダ式の$x$，$y$は全くの別物であるということです7．先の記憶領域の仕組みにより，$x$，$y$はそれぞれのラムダ式で独自に値の対応付けの管理が行われます． ↩

  7. レキシカルスコープ
    eval-apply2
    もし，あるラムダ式が別のラムダ式の変数を参照したい場合は，ラムダ式を返すラムダ式を定義して親子関係とし8，子が親の変数を参照可能とします．次は，引数$x$をとって『引数$y$をとって$x+y$を計算するラムダ式』を返すラムダ式の例です． ↩

  8. 高階関数（戻り値が関数）
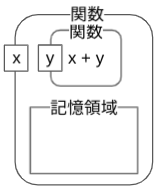
    lambda-closure3
    この式に値10を指定すると，引数xが10に対応付けられ，その対応付けを引き継いだ『引数$y$をとって$x+y$を計算するラムダ式』が返ります．最初のラムダ式の例と同じく，ラムダ式だけが返っても『関数だよ』という表示しか行われません． ↩

  9. 末尾再帰ではない再帰表現 ↩

  10. Uコンビネータ ↩

  11. 関数型プログラミング ↩

1
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?