純LISPを用いたプログラミング一時間体験講座

この記事は，LISP系言語全般をほとんど知らない，けれども他の言語でプログラミングに触れた経験がある人向けに，最低限の記述方法と応用例をまとめたものです．なお，LISPは多くの方言に分かれていることから，この記事では当方がシェルスクリプトで簡易実装した純LISP処理系にて実行例を示しています．

主に想定される読者

• LISP系言語をほとんど知らず，とりあえずどのような言語か知っておきたい．
• LISPによるリスト処理やラムダ式の基本的なところを把握しておきたい．
• 最低限のLISP仕様と応用例を知ることで，言語処理系実装の参考としたい．
• 純LISP（Pure Lisp）の定義についてツッコミを入れ考察・議論したい．

記事内容は，最初のLISP実行例と基本的なプログラミングで概ね一時間，残りの応用例を関心に応じて読み進めるという構成となっています．なお，この記事は下記拙作記事の統廃合・整理版です．

• Schemeプログラミング一時間体験講座
• Common Lispプログラミング一時間体験講座

純LISPの仕様と言語処理系

『純LISP』という言葉には明確な定義がなく，最低限必要な要素で構成されたLISP，といった程度の捉え方しかありません．また，LISP系言語全般に言えることですが，基本関数・構文の機能や名称もまちまちです．そこで，この記事では，最低限必要な要素で構成されたLISP処理系を独自実装することで，その言語仕様を示すことにしました．仕様の構成概要は次の通りです．

• 基本関数：cons car cdr eq atom
• 基本構文：quote lambda def
• 追加構文：macro
• 追加関数：length

独自処理系はシェルスクリプトで実装しており，次のGitHubリポジトリでパブリックドメイン（CC0, Creative Commons Zero v1.0 Universal）として開発・公開しています．『PureLISP.sh』と呼んでおり，この記事では，実行スクリプトのファイル名としています．

POSIX仕様で簡易実装していますので，ほとんどのコンピュータ環境で実行できると思います．たとえば，Windowsで利用できる『busybox-w32』を用いた実行例は次の通りです．S>はプロンプトです．なお，ひとつのまとまったLISP記述を実行（評価）するには，空行を一行入れる必要があることに注意して下さい．exitで処理系を終了できます．

C:\Users\TAKIZAWA Yozo\busybox>busybox.exe sh PureLISP.sh
S> (car '(10 20))

10
S> (cdr '(10 20))

(20)
S> (car (cdr '(10 20)))

20
S> (cons '10 (cons '20 nil))

(10 20)
S> exit


C:\Users\TAKIZAWA Yozo\busybox>

また，シェルを利用していることもあり，あらかじめLISPプログラムをテキストファイルに記述しておき，リダイレクトで読み込ませることもできます．プロンプトを表示しない-sオプションを併用すると結果表示が見やすくなります．ただし，テキストファイルに記述する際にも，ひとつのまとまったLISP記述の後には空行を一行入れる必要があることに注意して下さい．

$ cat examples/reduce.plsh
(def reduce
  (lambda (f L i)
     (cond ((eq L nil) i)
           (t (f (car L) (reduce f (cdr L) i))))))

(def list1 '(a b c))

(def list2 '(d e f g))

(reduce cons list1 list2)

(def rappend (lambda (x y) (reduce cons x y)))

(def list3 '((a b) (c d e) (f) (g h i)))

(reduce rappend list3 nil)

exit

$ sh PureLISP.sh -snl < examples/reduce.plsh
reduce
list1
list2
(a b c d e f g)
rappend
list3
(a b c d e f g h i)

【補足】
今回の記事につきましては，プログラミング内容に関するコメントや編集リクエストだけでなく，『PureLISP.sh』そのものへの御意見等（GitHubのIssues/Forkを含む）も受け付けます．ただし，記事の趣旨もあって，最低限必要な要素で構成されたLISP処理系を志向すること，POSIX準拠のシェルスクリプトで実装すること，パブリックドメインにて開発・公開することは維持します．他のプログラミング言語よる簡易LISP処理系実装については，こちらの記事を参考にして下さい．

基本的なLISPプログラミング

リスト構造とコンスセル

LISP系言語では，基本的なデータ構造として連結リストを多く用います．要素が先頭から芋づる式に連なっており，先頭から要素を順番にたどって様々な処理を行うのに向いているデータ構造です．

次は，LISPの記述方式であるS式を用いてリスト構造を示した実行例です．括弧と空白で要素の連なりを表現しています．なお，リストの要素としてリストを設けることができます．

S> '(a b c)

(a b c)
S> '(a (hoge 10) (hage 20))

(a (hoge 10) (hage 20))

'（シングルクォート）は，関数の実行と区別するために付けています．'を付けない場合は，リストの先頭要素が関数名，残りの要素がその関数への引数とみなされます．次は，リストの先頭要素を参照する基本関数car，残りの要素をもつリストを参照する基本関数cdrを実行した例です．

S> (car '(a (hoge 10) (hage 20)))

a
S> (cdr '(a (hoge 10) (hage 20)))

((hoge 10) (hage 20))

上記のcarおよびcdrの説明は，実は実際の処理とは大きく異なります．といいますのも，LISPにおける連結リストは，コンスセルと呼ばれる基本データ構造を基にしているためです．次の図は，上記の(a (hoge 10) (hage 20))の処理系内部でのデータ構造をボックス記法によって表現したものです．

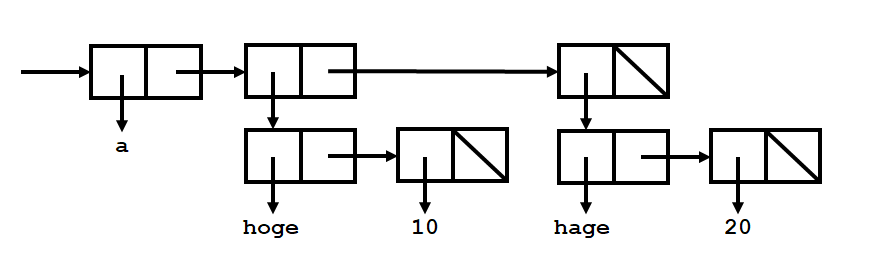
ふたつのセル（ボックス）がつながった表現が，ひとつのコンスセルを表しています．それぞれのセルは，アトムと呼ばれる数値や文字列などの基本データ（この記事の処理系ではシンボルのみを扱います）またはコンスセルを指し示すか，もしくは，図の斜線のように何も指し示さないかのいずれかとなります．そして，左側のセルをCAR部，右側のセルをCDR部と読んでいます．

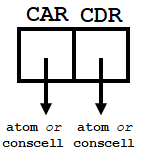
基本関数car，cdrは，このCAR部，CDR部を取り出しているに過ぎません．

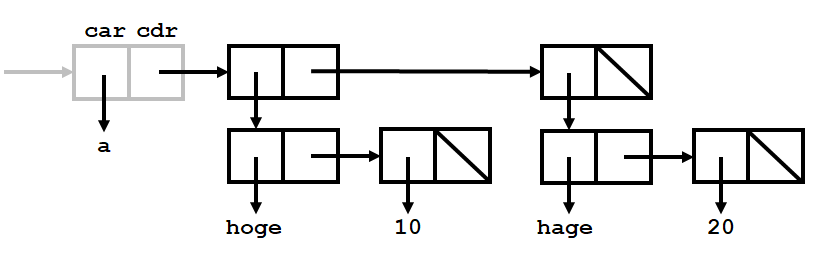
したがって，LISPでは連結リストだけでなく，コンスセルで表現できる他のデータ構造も扱うことができます．たとえば，コンスセルを作成する基本関数consを用いて，次のようなデータ構造を作成できます．なお，アトムにも'を付けることで，関数の名前ではないことを示しています．

S> (cons 'a 'b)

(a . b)

この.と( )によるふたつの要素で構成されるS式表現をドット対と呼びます．consを用ると，(a b c)は次のように構成することができます．

S> (cons 'a (cons 'b (cons 'c nil)))

(a b c)

nilは，上記の図の斜線の何もないことを表しています．この記事の処理系では，nilを空リスト()と等しいものとして扱っています．

S> nil

()
S> '()

()

ドット対は，シングルクォートを用いた表記でも可能です．

S> '(a . (b . (c . nil)))

(a b c)

上記の実行結果からわかるように，リスト表現(XX XX ... XX)は，(XX . (XX . (... (XX . nil)...)))を簡略した表現として扱われ，自動的に変換されます．ちなみに，'も基本構文quoteを簡略した表現であり，(a b c)は，本来であれば，consとquoteを用いて次のように作成することになります．

S> (cons (quote a) (cons (quote b) (cons (quote c) nil)))

(a b c)

ですが，多用される連結リストを表現するためにドット対やquote，consを用いていてはとても煩雑であるため，S式の入力においても簡略表現を利用することができます．

ところで，コンスセルによる連結リストは，CAR部がリストの要素，CDR部が次のコンスセルを指し示すことで構成されます．では，この逆を行うとどのようになるでしょうか？実行結果は次の通りです．

S> (cons (cons (cons nil 'a) 'b) 'c)

(((() . a) . b) . c)

【注意】
LISPの方言と呼ばれるプログラミング言語の中には，コンスセルは扱わず，連結リストのみ扱う場合があります．そのような言語でもcar cdr consが利用できる場合がありますが，それぞれ『リストの先頭要素の参照』『残りの要素をもつリストの参照』『先頭に要素を加えたリストを生成』のみとなります．例：Clojure，Hy

ラムダ式と名前束縛

まとまった処理をもつ関数を定義するには基本構文lambdaを用い，その記述はラムダ式と呼ばれます．次は，リストの引数をひとつとって二番目の要素を参照する関数処理を定義した時の実行例です．

S> (lambda (x) (car (cdr x)))

(lambda (x) (car (cdr x)) ())

このままではラムダ式を表現しただけですので，実際に値を与えて実行してみます．名前が付いている関数と同じく，リストの第一要素にラムダ式を，第二以降の要素に引数を記述します．

S> ((lambda (x) (car (cdr x))) '(a b c d e))

b

このままでは，二番目の要素を参照するプログラムが必要となるたびにラムダ式を記述しなければなりませんので，名前を付けます．ラムダ式に名前を付けたり，名前としての引数が実行時に具体的な値に対応付けられることを名前束縛といいますが，他の多くのプログラミング言語における『変数に代入する』こととは異なることに注意して下さい．

この記事で用いている処理系では，他のどのラムダ式の中からでも呼び出せるようグローバル空間で名前を付ける基本構文として，defを用います．

S> (def second (lambda (x) (car (cdr x))))

second
S> (second '(a b c d e))

b

ラムダ式以外にも，シングルクォートで表現されたデータ構造にも名前をを付けることができます．結果として，処理記述もデータも，共に名前に対する値として扱うことになります．

S> (def second (lambda (x) (car (cdr x))))

second
S> (def L '(a b c d e))

L
S> (second L)

b

この記事の処理系では，ラムダ式の中で利用できる処理として，基本関数cons car cdrの他に，判断分岐のための基本構文condと，条件式を記述するための基本関数eqとatomがあります．基本構文condは，条件式と，その条件式が真の時に行わせたい処理を括弧でセットにして記述します．

S> (def one 'a)

one
S> (def two 'b)

two
S> (cond ((eq one two) 'yes) (t 'no))

no
S> (def two 'a)

two
S> (cond ((eq one two) 'yes) (t 'no))

yes

基本関数eqは，ふたつの引数のアトムが等しいか否かを判断して真偽値を返します．この処理系では，真がt，偽がnil（『何もない』ことや空リスト()と兼用）です．アトムですので，リストを含むコンスセル構造は比較対象外となり，その際にはnilが返されます．もし，値がアトムか否かを判断したい場合は，基本関数atomを用います．

S> (atom 'hoge)

t
S> (atom '(hoge))

()

上記のcondの例では，最後の条件式として真の値であるtが記述されています．これは，condが条件式と真の時の処理のセットについて最初から順番に確認し，条件式が真となった時に対応する処理を行い，その時点で判断分岐を終えることから，他の条件式が全て偽だった時の処理を記述するためです．

次は，引数の値が0の時にzeroを，1の時にoneを，それ以外はothersを返す関数定義の例です．

S> (def func
     (lambda (x)
       (cond ((eq x '0) 'zero)
             ((eq x '1) 'one)
             (t 'others))))

func
S> (func '0)

zero
S> (func '1)

one
S> (func '2)

others

ここで気をつけたいのは，この記事の処理系では数値を扱えないということです．上記の例で0や1を用いていますが，あくまで文字の羅列としての値＝シンボル（記号）でしかありません．アルファベットを用いた文字の羅列もシンボルであり，文字列でもないことに併せて注意して下さい．

ラムダ式に名前を付けることができると，自分自身を呼び出す再帰関数を定義することができます．次は，キーワードと値をコンスセルでセットにしたもののリスト（辞書型や連想配列に相当）から，キーワード検索して対応するセットを返す関数assocを定義・実行した例です．

S> (def assoc
     (lambda (k vs)
       (cond ((eq vs nil) nil)
             ((eq k (car (car vs)))
              (car vs))
             (t (assoc k (cdr vs))))))

assoc
S> (assoc 'Orange '((Apple . 120) (Orange . 210) (Lemon . 180)))

(Orange . 210)
S> (def ret (assoc 'Orange '((Apple . 120) (Orange . 210) (Lemon . 180))))

ret
S> (car ret)

Orange
S> (cdr ret)

210
S> (assoc 'Nashi '((Apple . 120) (Orange . 210) (Lemon . 180)))

()

第二引数のリストが空リストnilの時は，偽を表すnilを返します．そうでない時は，次に，第一引数のキーワードkの値と，第二引数のリストのCAR部のCAR部(car (car vs))，すなわち，先頭のセットのキーワードと比較します．一致すれば，その先頭のセットを返して終わりです．以上のいずれでもない場合は，第二引数の先頭のセットは該当しませんので，先頭のセットを除いたリスト(cdr vs)を新しく第二引数として，自分自身であるassocを再帰的に呼び出しています．

ところで，先に『処理記述もデータも名前に対する値として扱う』と述べました．これは，ラムダ式の引数の値として，ラムダ式（関数）を与えることができることを意味します．次は，関数型プログラミングでは有名なmapを定義・実行した例です（ただし，引数としてリストを必ずひとつのみとるバージョンとなります）．第二引数の関数を第三引数のリストの各要素に対して処理を行い，その結果を再びリストにして返します．

S> (def map
     (lambda (f x)
        (cond ((eq x nil) nil)
              (t (cons (f (car x))
                       (map f (cdr x)))))))

map
S> (def vs '((hoge . 10) (hage . 20) (hige . 30)))

vs
S> (map car vs)

(hoge hage hige)
S> (map cdr vs)

(10 20 30)

【注意】
上記で扱った基本関数・基本構文の名称や文法・機能は，LISPの方言や処理系によってまちまちです．コンスセルを扱うLISP系言語については，cons car cdrのみが共通と考えた方が良いでしょう．

応用例

リスト処理による数値表現

ラムダ式の説明にて，『この記事の処理系では数値を扱えない』と述べました．実のところ，原初のLISPでも数値は想定されておらず，値は全てシンボル（記号）とコンスセル構造のみで表現しています．これは，プログラムを処理する評価器のみを実装できれば良かったためで，それには，基本5関数（この記事の処理系でいうcons car cdr eq atom）とラムダ式および判断分岐構文があるだけで実装できます．すなわち，評価器を記述するために必要な最低限の機能を実装する評価器（超循環評価器）という構成となっており，この必要最低限のLISP仕様を『純LISP』と呼ぶ場合が多いという状況です．

では，この必要最低限の機能だけでは絶対に数値を扱うことができないのかというとそんなことはなく，実用性はないものの，リストの要素数を数値とみなすことで，0以上の整数や演算を比較的簡単に表現することができます．次は，0の値，+1を行う関数，-1を行う関数を定義した例です．

S> (def zero nil)

zero
S> (def inc (lambda (x) (cons 'n x)))

inc
S> (def dec (lambda (x) (cdr x)))

dec
S> (def one (inc zero))

one
S> (eq (dec one) zero)

t

この考え方を用いて，フィボナッチ数を計算するプログラムを作成してみましょう．まず，フィボナッチ数$F_n$の定義は次の通りです．

F_0=0 \\
F_1=1 \\
F_n=F_{n-1}+F_{n-2}

今回の場合，三行目の$+$（足し算）に相当するのは，ふたつのリストの要素の合成となります．ここで，この処理を行う関数addの定義を考えます．たとえば，$1+3=4$は次のように表現されます．

(add '(n) '(n n n))
⇒ (n n n n)

まず，第一引数として指定されたリストx，第二引数として指定されたリストyのうち，xが要素なしの空リスト()だった時は，$0+y$に相当しますから，yをそのまま返すことにします．

(add '() '(n n n)
⇒ (n n n)

xが空リストではなかった場合は，xの先頭要素を除いたリスト(cdr x)とyについて，add自身を呼び出して再帰処理を行います．$1+3$の場合，cdrによって$1$が$0$となりますから，add自身を呼び出す際の引数は，上記のリストxが空リストの時と同じ処理となります．

(add (cdr '(n) '(n n n)))
⇒ (add '() '(n n n))
⇒ (n n n)

そこに，xの先頭要素を再びconsによって追加すれば，要素を合成したリストが得られることになります．

(cons 'n (add (cdr '(n)) '(n n n)))
⇒ (cons 'n '(n n n))
⇒ (n n n n)

以上の記述を組み合わせれば，関数addを定義することができます．

S> (def add
     (lambda (x y)
       (cond ((eq x nil) y)
             (t (cons (car x)
                      (add (cdr x) y))))))

add
S> (add '(n n) '(n n n))

(n n n n n)

数値を扱う準備ができましたので，フィボナッチ数を計算する関数fibを定義します．

S> (def fib
     (lambda (n)
       (cond ((eq n nil) nil)
             ((eq (cdr n) nil) '(n))
             (t (add (fib (cdr n))
                     (fib (cdr (cdr n))))))))

fib

早速，$F_{10}$を求めてみましょう．複数の関数を間違いのないよう定義して実行する必要がありますので，あらかじめテキストファイルfib.plshにプログラムを記述し，リダイレクトで実行してみます．

$ cat fib.plsh
(def add
  (lambda (x y)
    (cond ((eq x nil) y)
          (t (cons (car x)
                   (add (cdr x) y))))))

(def fib
  (lambda (n)
    (cond ((eq n nil) nil)
          ((eq (cdr n) nil) '(n))
          (t (add (fib (cdr n))
                  (fib (cdr (cdr n))))))))

(fib '(n n n n n n n n n n))

exit

$ sh PureLISP.sh -s < fib.plsh
add
fib
(n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n)

さあ，結果として表示された要素数を数えてみましょう…というのはとても厳しいので，この記事の処理系の追加組込関数である，リストの要素数を返す関数lengthを用いて確認してみます．

$ cat fib.plsh
（省略）
(length (fib '(n n n n n n n n n n)))

exit

$ sh PureLISP.sh -s < fib.plsh
add
fib
55

ところで，上記の処理はとても時間がかかります．フィボナッチ数計算一般に言えることですが，定義をそのままプログラムにすると，自分自身を1回呼び出すごとに，更にそこからそれぞれ2回呼び出して計算していくことになるためです．

そこで，自分自身を呼び出した結果を用いて計算するのではなく，計算を行ってから自分自身を呼び出すようにすることで，計算を後回しにして溜め込んでいくことがないようにします．この処理を行うため，途中結果を参照する引数をふたつ増やします．

$ cat fib2.plsh
(def add
  (lambda (x y)
    (cond ((eq x nil) y)
          (t (cons (car x)
                   (add (cdr x) y))))))

(def fib2
  (lambda (n f1 f2)
    (cond ((eq n nil) f1)
          (t (fib2 (cdr n)
                   f2
                   (add f1 f2))))))

(length (fib2 '(n n n n n n n n n n) nil '(n)))

exit

$ sh PureLISP.sh -s < fib2.plsh
add
fib2
55

後者のスタイルは末尾再帰と呼び，実質的には，単純な繰り返し処理に相当します．処理系によっては，末尾再帰処理を本当の繰り返し処理に変換して実行する『末尾再帰最適化』が行われ，関数呼び出しが繰り返されても高速に実行することが可能です．

ところで，既にお気づきもしれませんが，必要最低限な機能をもつLISP仕様には，繰り返し処理を行う構文も存在しません．LISP系言語では，上記の末尾再帰最適化などを前提に，繰り返し処理を再帰関数で定義することがよく行われます．

高階関数による不動点コンビネータ

ラムダ式の説明で，lambdaを用いた関数定義は，他の関数に渡す値とすることができると述べました．多くのLISP系言語では，関数定義の中でlambda式を新しく記述して，関数の処理結果としてその新しいlambda式，すなわち，関数定義を返すことができます．このように，関数を引数の値としたり戻り値としたりする関数を高階関数と呼びます．

ここでは，高階関数の機能を用いて，不動点コンビネータと呼ばれる無名再帰関数を実行するための関数を定義してみたいと思います．無名関数とはラムダ式のみのことですが，再帰関数を定義するには，自分自身を呼び出すために名前が必要であるため，通常であれば，無名再帰関数は定義・実行できません．しかし，不動点コンビネータを用いれば，引数のひとつを自身を呼び出す名前として扱うことができ，再帰処理が可能となります．

このような不動点コンビネータとして最も有名なのが，自身も無名関数であるYコンビネータと呼ばれる定義ですが，ここではよりシンプルな定義として，名前をもつ不動点コンビネータfixを定義・利用してみます．不動点コンビネータとは，次の式が成り立つ関数$g$を指します．

$$g(f)=f(g(f))$$

ここでは，任意の関数$f$が無名再帰関数に相当します．そこでまず，この関数$g$をfixという名前でそのまま定義してみます．

S> (def fix (lambda (f) (f (fix f))))

fix

うまく定義できたように見えますが，実は，うまくいっていません．といいますのも，LISP系言語では引数の実行（評価）を先に行うことになっており，このままでは，(f (fix f))について，(fix f)がfより先に実行されて無限ループに陥ってしまうためです．そこで，(fix f)よりも前にfを実行するため，(fix f)を更にラムダ式の本体として(lambda (x) ((fix f) x))とし，実質的な遅延評価をさせるようにします．

S> (def fix (lambda (f) (f (lambda (x) ((fix f) x)))))

fix

LISP系言語の多くではレキシカルスコープを採用しており，それぞれのラムダ式は，グローバル空間とは別に，内部に独自の名前空間をもっています．このことについて，簡単な例で確認してみます．

S> (def f1 (lambda (arg1) (cons arg1 arg2)))

f1
S> (def f2 (lambda (arg2) (f1 'a)))

f2
S> (def arg2 'c)

arg2
S> (f2 'd)

(a . c)

関数f2はf1を実行する際に引数としてaを渡しますので，f1の(cons arg1 arg2)のうちのarg1はaとなります．では，f1の(cons arg1 arg2)のうちのarg2の値はどのように決まるでしょうか？関数f2の本体で呼ばれているので，f2の引数arg2の値であるdでしょうか？レキシカルスコープの場合，関数f1のラムダ式は独自の名前空間をもっているため，たとえ関数f2の本体から呼ばれたとしてもf2のarg2には名前束縛されず，唯一参照できる，defによって定義されたグローバル空間で名前束縛されているcが参照されます．

したがって，関数fixの定義における(lambda (f) (f (lambda (x) ((fix f) x))))についても，最初のfは(lambda (f) ...)のfに名前束縛されますが，(lambda (x) ((fix f) x))のfは束縛されず，(lambda (x) ((fix f) x))が戻り値として評価される際のfに束縛されます．同じ無名再帰関数に束縛はされますが，別のものとして扱われることから，評価に遅延が発生しています．この，戻り値としてのラムダ式に内包された名前空間はクロージャと呼ばれています．

さて，定義したfixを用いて，無名再帰関数を実行してみましょう．『リスト処理による数値表現』で登場した，フィボナッチ数を求める関数（末尾再帰ではない方）を，次のように無名関数化します（lambda fibをlambda (fib)に置き換えただけですが）．

(lambda (fib)
  (lambda (n)
    (cond ((eq n nil) nil)
          ((eq (cdr n) nil) '(n))
          (t (add (fib (cdr n))
                  (fib (cdr (cdr n))))))))

そして，これを不動点コンビネータfixの引数として指定します．fixの戻り値がやはりラムダ式なので，第二要素にフィボナッチ数を求める順番を記述したリストとし，最終的な戻り値をlengthで数値化します．今回もテキストファイルにプログラムを記述し，リダイレクトで実行しています．

$ cat fixfib.plsh
(def add
  (lambda (x y)
    (cond ((eq x nil) y)
          (t (cons (car x)
                   (add (cdr x) y))))))

(def fix (lambda (f) (f (lambda (x) ((fix f) x)))))

(length
  ((fix
     (lambda (fib)
       (lambda (n)
         (cond ((eq n nil) nil)
               ((eq (cdr n) nil) '(n))
               (t (add (fib (cdr n))
                       (fib (cdr (cdr n)))))))))
   '(n n n n n n n n n n)))

exit

$ sh PureLISP.sh -s < fixfib.plsh
add
fix
55

マクロによるメタプログラミング

純LISPの範疇ではありませんが，ほとんどのLISP系言語にはマクロの機能があります．ラムダ式によく似ているのですが，ラムダ式が処理そのものを定義するのに対し，マクロは処理を行う記述の生成を定義します．この機能によって，プログラム上で新しい構文を導入することが可能となります．

この記事で用いている処理系にもマクロ機能がありますので，実際に利用例を見てみましょう．次は，関数定義専用の構文defunを定義した例です．既存の構文であるdefやlambdaが，シングルクォートで基本データ（シンボル）扱いされていることに注意して下さい．

(def defun
  (macro (name args body)
    (list 'def name (list 'lambda args body))))

上記で用いられているlistは，任意個の引数をとってリストを作成する関数です．詳細は省きますが，今回の処理系では次のように定義して利用することが可能です．

S> (def list (lambda x x))

list
S> (list 'a 'b 'c)

(a b c)
S> (list '(a b) 'c '(d e))

((a b) c (d e))

マクロ定義したdefunは，次のように用いることができます．

S> (def list (lambda x x))

list
S> (def defun
     (macro (name args body)
       (list 'def name (list 'lambda args body))))

defun
S> (defun f (x) (cdr (cdr x)))

f
S> (f '(a b c))

(c)

なぜこのようなことが可能かを理解するため，処理の流れを順番に見ていきましょう．まず，macro構文はlambda構文と同じく，引数と処理内容を定義します．

S> (macro (name args body) (list 'def name (list 'lambda args body)))

(macro (name args body) (list (quote def) name (list (quote lambda) args body)) ())

このmacro構文の記述に引数の値を与えることで処理が行われますが，本体では具体的な処理が行われるのではなく，処理を行うためのS式が生成されます．例として，本体で用いられている引数の名前name args bodyに，defで値を割り当ててから，本体の処理記述である(list 'def name (list 'lambda args body))を実行してみます．

S> (def name 'f)

name
S> (def args '(x))

args
S> (def body '(cdr (cdr x)))

body
S> (list 'def name (list 'lambda args body))

(def f (lambda (x) (cdr (cdr x))))

出力されたS式は，defとlambda式を用いた関数定義記述そのものです．処理系は，上記のようにmacro構文で定義された処理に引数の値を適用（apply）することでプログラム記述を生成し，生成されたS式をあらためて評価（eval）することで，実際の処理を行います．これが，LISPにおけるマクロの仕組みです．

プログラムがプログラムを生成して実行することを，メタプログラミングと呼びます．他のプログラミング言語にも似たような機能がありますが，多くは文字列としてのプログラム記述の操作に留まっています．LISP系言語ではプログラムもデータも内部では同じS式ですので，S式データがそうであるように，既に実行しているS式プログラムの構文を書き換えながら処理を継続するということも可能です．

次は，(defun func1 (x y) (cons x y))という処理は全く変更せず，defunを通常の関数定義構文から，本体処理の書き換えを含む構文に変更している例です．

S> (def defun
     (macro (name args body)
       (list 'def name (list 'lambda args body))))

defun
S> (defun func1 (x y) (cons x y))

func1
S> (func1 'a 'b)

(a . b)
S> (def defun
     (macro (name args body)
       (list 'def name (list 'lambda args (cons 'list (cdr body))))))

defun
S> (defun func1 (x y) (cons x y))

func1
S> (func1 'a 'b)

(a b)

基本関数によるユーティリティ関数の定義

これまでの解説や例の中で，関数型プログラミングではおなじみのmapといったユーティリティ関数の定義を見てきました．これらは実用的な用途として用いられることから，組込関数として処理系内部で実装した方が速度面で良いのですが，今回の記事で用いている処理系は（どのような環境でも試しやすくするよう，シェルスクリプトによる）簡易実装でしかありませんので，実のところ，処理系内部で定義しても速度的にはあまり変わりません．

そのことを踏まえ，ここでは，多用されるユーティリティ関数の実際の定義例を見ていくことにします．理解してほしいのは，mapなどを用いたリスト処理を行うのが関数型プログラミングというわけではなく，それらは関数型プログラミングによって実現されている機能の一例である，ということです．

• Map

ここでは，処理対象のリストがふたつある場合，すなわち，指定する関数がふたつの引数をとる場合の関数map2の定義を示します．利用例として，基本関数consとふたつの同じ要素数をもつリストを引数の値としてとって実行するpairsを定義・実行しています．pairsによって，この記事の処理系におけるevalで指定する名前空間を比較的簡単に生成できます．

$ cat map2.plsh
(def map2
  (lambda (f a b)
     (cond ((eq a nil) nil)
           (t (cons (f (car a) (car b))
                    (map2 f (cdr a) (cdr b)))))))

(def pairs (lambda (a b) (map2 cons a b)))

(def exp '(cons (cons a b) (cons (cons a c) nil) nil))

(def env (pairs '(a b c) '(1 2 3)))

(eval exp env)

(def env (pairs '(a b c) '(hoge hage hige)))

(eval exp env)

exit

$ sh PureLISP.sh -snl < map2.plsh
map2
pairs
exp
env
((1 . 2) (1 . 3))
env
((hoge . hage) (hoge . hige))

• Filter

下記で定義されているfilterは，ある条件を満たす要素だけをリストから取り出す高階関数です．リストの各要素になんらかの判断を行うことができる関数を指定して『ふるいにかける』処理を行いますが，ここでは，再帰関数の解説で登場しました，キーワードと値をコンスセルでセットにした連想リストに対する処理を行ってみます．注目すべきは，指定関数が無名のラムダ式のままであるということで，条件を示すためだけのこのようなシーンでは，名前付けを行わずにラムダ式をそのままFilter関数で記述することがよく行われています．

$ cat filter.plsh
(def filter
  (lambda (f x)
     (cond ((eq x nil) nil)
           ((f (car x))
            (cons (car x) (filter f (cdr x))))
           (t (filter f (cdr x))))))

(def vs '((O . 1) (O . 2) (I . 10) (A . 20) (I . 3) (A . 30) (O . 4)))

(filter (lambda (x) (eq (car x) 'O)) vs)

exit

$ sh PureLISP.sh -snl < filter.plsh
filter
vs
((O . 1) (O . 2) (O . 4))

• Reduce

Reduce（またはFold）と呼ばれている処理は，引数として関数とリスト，そして初期値をとって畳み込みを行います．Mapがリストの要素それぞれに指定した関数を実行するのに対し，Reduceはリストの要素を指定した関数で連鎖的に実行していきます．連鎖的に処理を行うことから，ふたつの引数をとる関数をReduceの引数として指定することになります．

次の例では，関数reduceを定義し，引数としてconsを指定することで，ふたつのリストの要素を結合する処理を行っています．処理の流れとしては，第三引数の(d e f)に対して，第二引数の(a b c)を後ろ（右）の要素から次々と『畳み込んで』いく，すなわち，

S> (cons 'a (cons 'b (cons 'c '(d e f))))

(a b c d e f)

と同じ処理を行っています．

$ cat reduce.plsh
(def reduce
  (lambda (f L i)
     (cond ((eq L nil) i)
           (t (f (car L) (reduce f (cdr L) i))))))

(reduce cons '(a b c) '(d e f))

exit

$ sh PureLISP.sh -snl < reduce.plsh
reduce
(a b c d e f)

なお，上記のreduceとconsによるリスト要素の結合処理は，通常appendと呼ばれますが，reduceの処理をcons専用の関数として書き換えると，reduceなしで定義できます．この定義の方が，上記のconsによる処理との対応が取りやすいかと思います．

S> (def append
     (lambda (a b)
       (cond ((eq a nil) b)
             (t (cons (car a) (append (cdr a) b))))))

append
S> (append '(a b c) '(d e f))

(a b c d e f)

ところで，このappendを更にreduceで用いて畳み込み処理を行うことで，リスト内のリストの要素を『平坦化』させることができます．これは，任意の数のリストの要素を全て結合する処理にも相当します．

S> (reduce append '((1 2) (3) (4 5 6) (7 8)))

(1 2 3 4 5 6 7 8)

この平坦化処理も，次の通り，関数flattenとして直接定義することが可能です（ただし，appendは使用しています）．

S> (def flatten
     (lambda (L)
        (cond ((eq L nil) nil)
              (t (append (car L) (flatten (cdr L)))))))

flatten
S> (def append
     (lambda (a b)
       (cond ((eq a nil) b)
             (t (cons (car a) (append (cdr a) b))))))

append
S> (flatten '((1 2) (3) (4 5 6) (7 8)))

(1 2 3 4 5 6 7 8)

• その他

appendを用いた定義例のひとつに，リストの要素を逆順にする関数reverseがあります．

S> (def reverse
     (lambda (a)
       (cond ((eq a nil) nil)
             (t (append (reverse (cdr a))
                        (cons (car a) nil))))))

reverse
S> (reverse '(1 2 3 4 5 6 7 8))

(8 7 6 5 4 3 2 1)

リストの中に特定の要素が存在しているかを判定するために用いられるmemberというユーティリティ関数があります．次の例は，特定の要素が存在すれば，その要素以降のリストを返すというものです．このため，判定というよりは，通常のリスト処理のひとつとして定義されます．

S> (def member
     (lambda (k vs)
       (cond ((null vs) nil)
             ((eq (car vs) k) vs)
             (t (member k (cdr vs))))))

member
S> (member 'c '(a b c d e f g h i j))

(c d e f g h i j)
S> (member 'i '(a b c d e f g h i j))

(i j)
S> (member 'z '(a b c d e f g h i j))

()

備考

記事に関する補足

• 今回用いた自作処理系『PureLISP.sh』や，各プログラミング言語でも実装した原初LISP処理系，実は，この統廃合・整理版記事を作成したいがために実装を始めたという…．一時期，あらゆる言語で簡易LISP処理系が実装できるのが楽しくなってあさっての方向に意識が飛んでいたけど，なんとか戻ってこれた感じ．うん．
• 応用例については，もっと簡単な例を順次追加する予定．とはいえ，『リスト処理による数値表現』がないと数値は扱えないから，クロージャによるcons car cdrの実装例あたりからかなあ．あと，追加組込関数evalを用いた，なんちゃってメタプログラミングとか．後者は，原初LISP処理系ならすごく簡単だったんだよなあ…．【2020-10-31】なんちゃってメタプログラミングの例を追加．これって，『PureLISP.sh』にマクロを実装するのも簡単ってことなのだよな．どうしよっかな．【2020-11-04】マクロによるメタプログラミングの例に差し替え．やはりマクロはLISPの真髄のひとつですな．

変更履歴

• 2020-11-04：メタプログラミングの例をevalからmacroに変更
• 2020-11-01：応用例に『基本関数によるユーティリティ関数の定義』を追加
• 2020-10-31：応用例に『評価器呼び出しによるメタプログラミング』を追加
• 2020-10-30：初版公開