TOPIXcore30銘柄のクラスタリング分析

はじめに

TOPIXcore30銘柄の株価変化率のデータにクラスタリング分析をかけることにした。
データはYahoo Financeからライブラリ（yfinance）を利用して取得した。

コード

データをGoogle Driveに保存するまで

Google Driveのマウント

from google.colab import drive
drive.mount('/content/drive')

必要なライブラリをインポート

# 必要なライブラリをインポート
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import yfinance as yf
from datetime import datetime, timedelta

TOPIX Core30銘柄の株価を取得してGoogleドライブに保存

同じデータを使って分析を行うことになる場合も多いだろうから、取得したデータをGoogleドライブにcsvで保存しておく。しかし、 TOPIX Core30は結構銘柄入れ替えしてて、構成銘柄をキチンと拾うのが面倒。

# TOPIX Core30の構成銘柄
tickers = ['3382.T', '4063.T', '4502.T', '4503.T', '4568.T', '6098.T', '6273.T', '6367.T', 
           '6501.T', '6594.T', '6758.T', '6861.T', '6954.T', '6981.T', '7203.T', '7267.T', 
           '7741.T', '7974.T', '8001.T', '8031.T', '8035.T', '8058.T', '8306.T', '8316.T', 
           '8411.T', '8766.T', '9432.T', '9433.T', '9434.T', '9984.T']

# 銘柄と会社名の辞書
company_names = {
    '3382.T': 'Seven&I', '4063.T': 'ShinEtsu', '4502.T': 'Takeda', 
    '4503.T': 'Astellas', '4568.T': 'DaiichiSankyo', '6098.T': 'Recruit', '6273.T': 'SMC', '6367.T': 'Daikin', 
    '6501.T': 'Hitachi', '6594.T': 'Nidec', '6758.T': 'Sony', '6861.T': 'Keyence', '6954.T': 'Fanuc', 
    '6981.T': 'MuRata', '7203.T': 'Toyota', '7267.T': 'Honda', '7741.T': 'HOYA', '7974.T': 'Nintendo', 
    '8001.T': 'ITOCHU', '8031.T': 'Mitsubishi Corp', '8035.T': 'Tokyo Electron', '8058.T': 'Mitsubishi Trading', 
    '8306.T': 'MUFG', '8316.T': 'SMBC', '8411.T': 'Mizuho', '8766.T': 'Tokio Marine', 
    '9432.T': 'NTT', '9433.T': 'KDDI', '9434.T': 'SoftBank', '9984.T': 'SoftBankG'
}

# 株価データを取得
data = yf.download(tickers, period="max")['Adj Close']

# 現在の日付を取得
now = datetime.now()

# 日付を文字列に変換（形式：年-月-日）
date_str = now.strftime("%Y-%m-%d")

# Google DriveのパスにデータをCSVファイルとして保存
data.to_csv(f'/content/drive/MyDrive/stock_data_{date_str}.csv')

これで、株価データが今日の日付（2023/5/17）を入れたファイル名"stock_data_20230517.csv"として保存された。

クラスタリング分析の実行

株価データの再読み込みと株価変化率の計算

保存したデータ"stock_data_20230517.csv"を呼び出して、日々の株価変化率を計算する。

# CSVファイルの再読込
data = pd.read_csv('/content/drive/MyDrive/stock_data_2023-05-17.csv', index_col=0)

### 日次変化率を計算
returns = data.pct_change()

### 欠損値を削除
returns = returns.dropna()

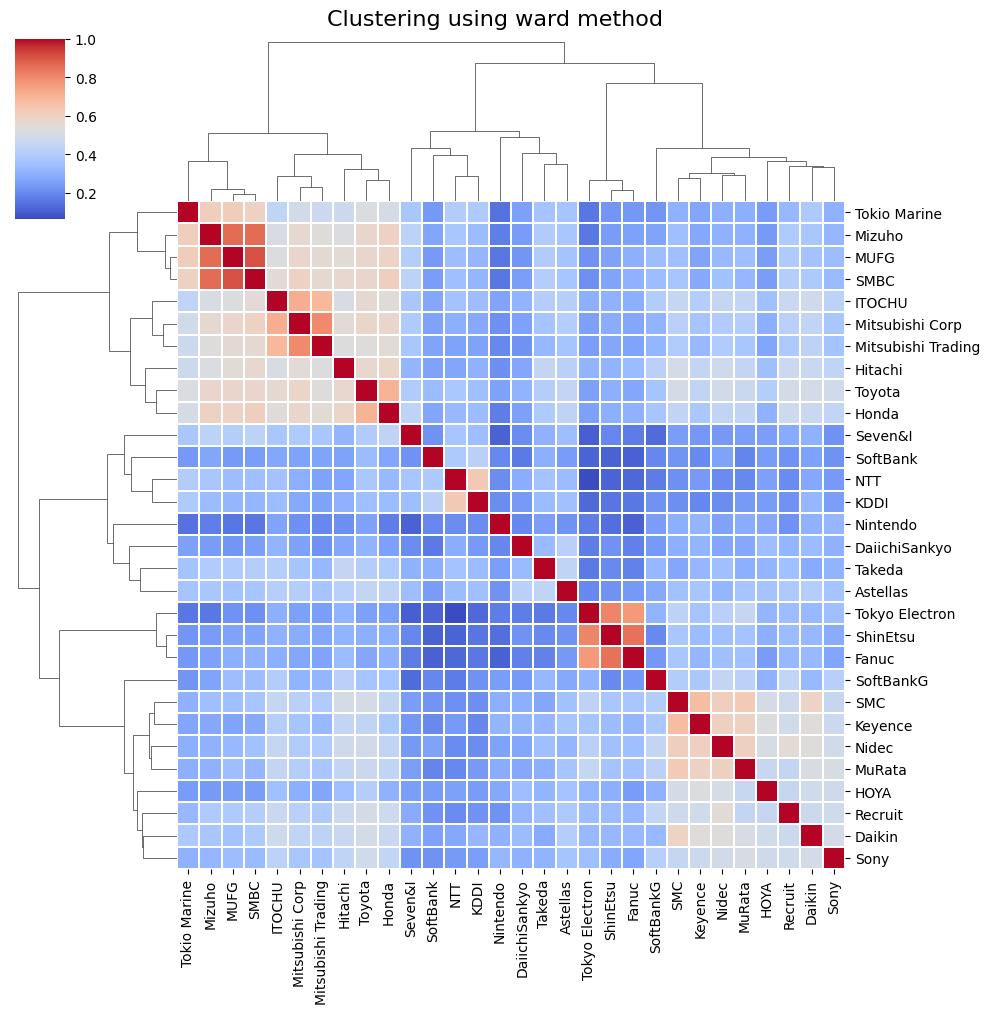
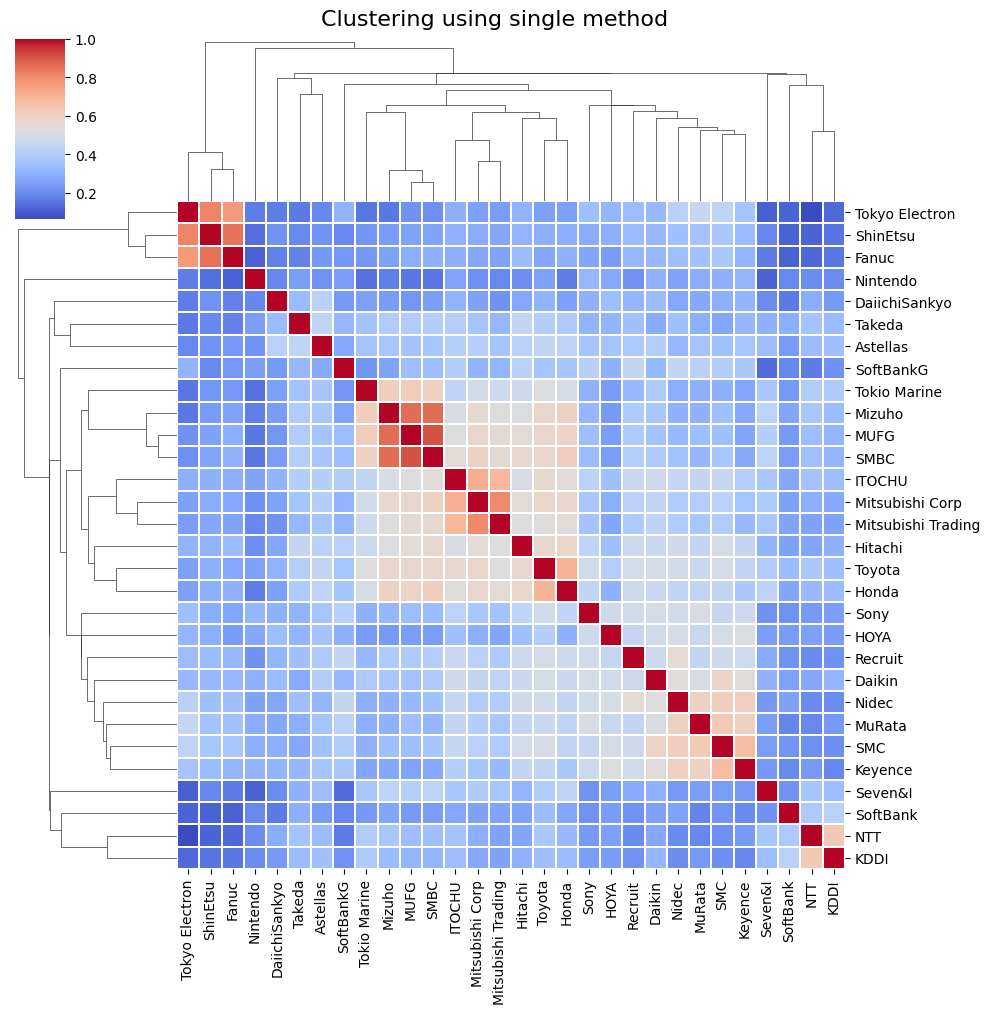
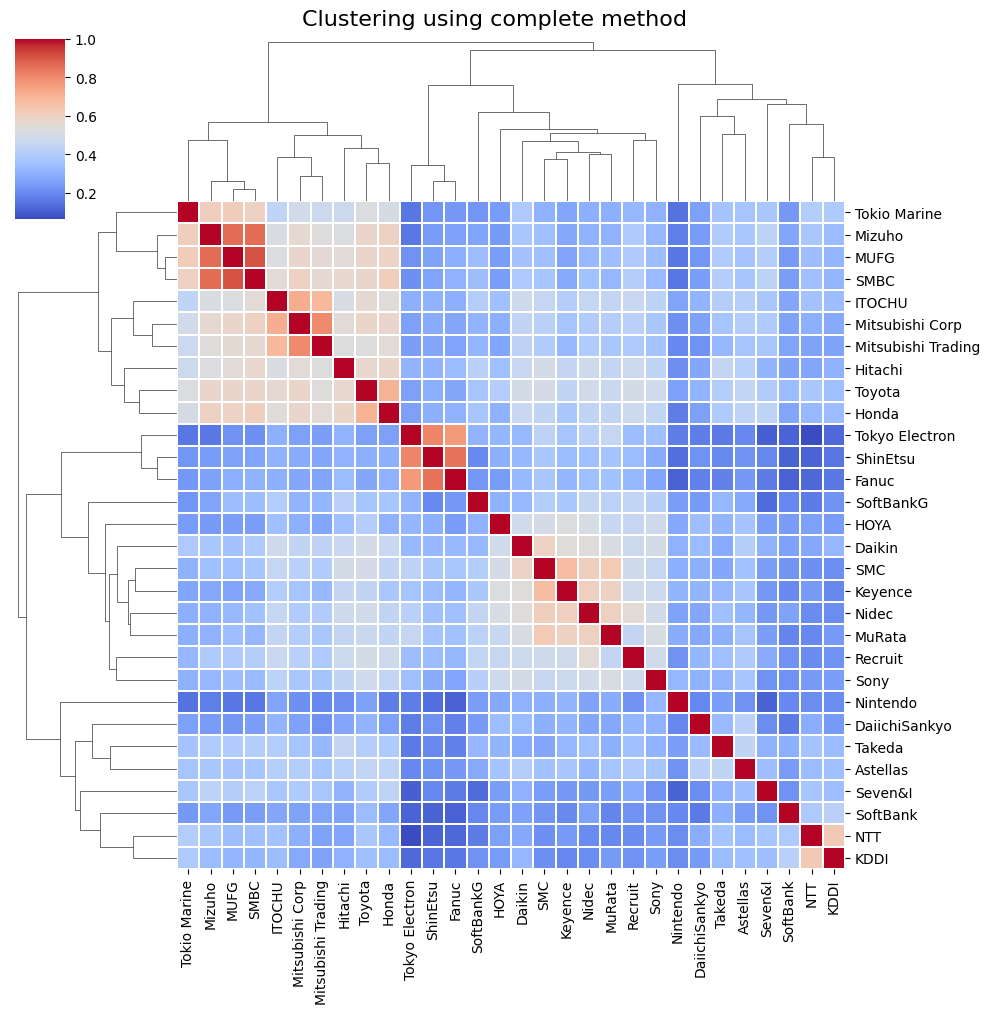
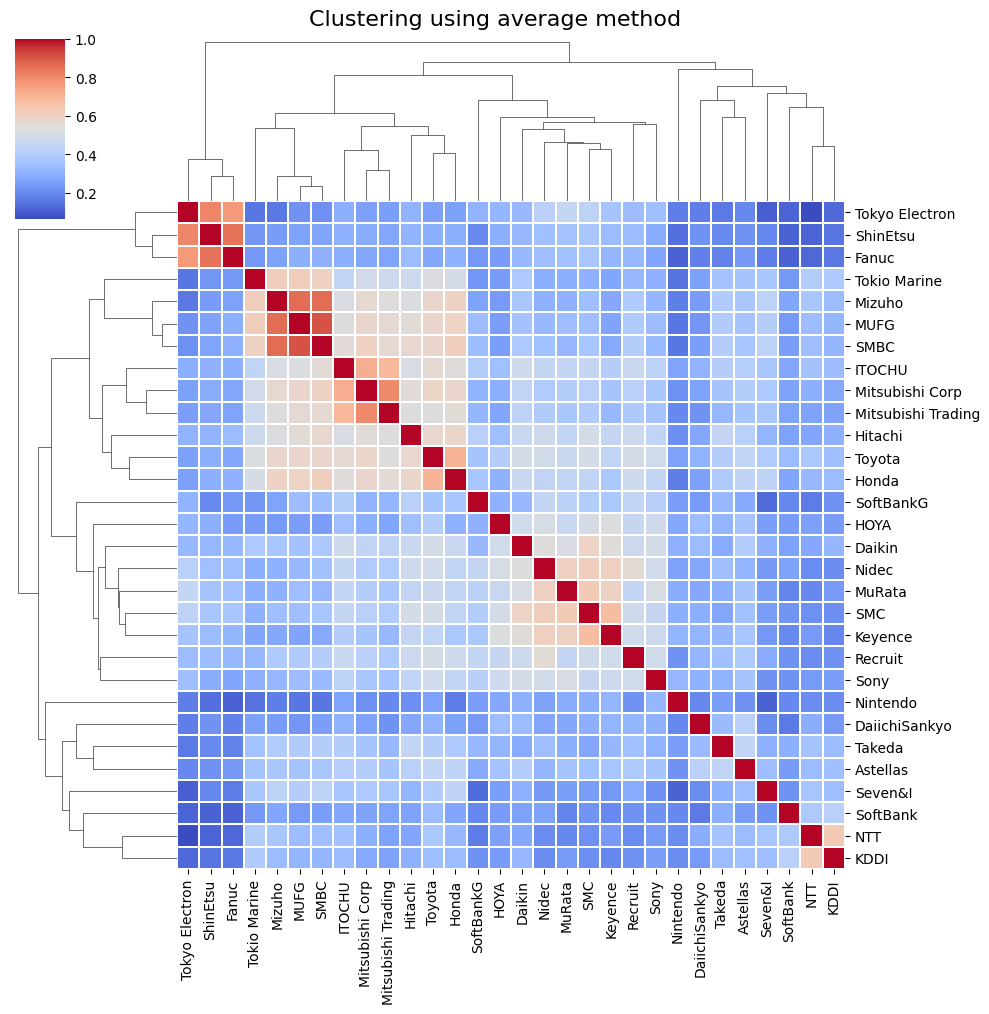
階層的クラスタリング分析

各種の階層的クラスタリング手法を試みることにした。

# クラスタリング手法のリスト
methods = ['ward', 'single', 'complete', 'average']

for method in methods:
    g = sns.clustermap(returns.corr(), cmap='coolwarm', linewidths=0.1, 
                       xticklabels=[company_names[ticker] for ticker in returns.columns], 
                       yticklabels=[company_names[ticker] for ticker in returns.columns], 
                       method=method)
    
    plt.setp(g.ax_heatmap.get_xticklabels(), rotation=90)  # x軸のラベルを90度回転
    g.fig.suptitle(f'Clustering using {method} method', fontsize=16, y=1.01)  # タイトルを設定し、少し上にずらす
    plt.show()

階層的クラスタリング手法による出力結果（ヒートマップ）

それぞれの手法ごとに描画したところ、以下の図が描けた。

非階層的クラスタリング

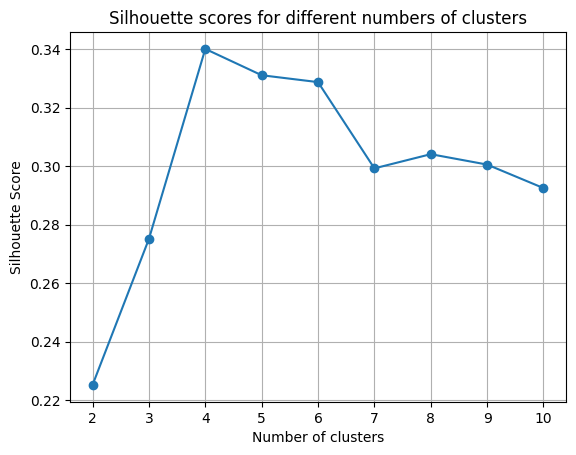
以下では、非階層的クラスタリング手法のうちk-means法によってみる。クラスター数はシルエット法によって決めることにした。

# 必要なライブラリの追加インポート
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score, silhouette_samples
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# クラスタ数の候補
n_clusters_candidates = list(range(2, 11))

# 各クラスタ数でのシルエットスコアを保存するリスト
silhouette_scores = []

# クラスタ数の候補ごとにk-means法とシルエット法を適用
best_n_clusters = None
best_silhouette_score = -1
best_labels = None
best_silhouette_vals = None
for n_clusters in n_clusters_candidates:
    # クラスタリングモデルを作成
    kmeans = KMeans(n_clusters=n_clusters, n_init=10)
    
    # 変動の相関行列に対してクラスタリングを実行
    kmeans.fit(returns.corr())
    
    # クラスタリング結果を取得
    labels = kmeans.labels_
    
    # シルエットスコアを計算
    score = silhouette_score(returns.corr(), labels)
    
    # 各サンプルのシルエットスコアを計算
    silhouette_vals = silhouette_samples(returns.corr(), labels)
    
    # シルエットスコアをリストに追加
    silhouette_scores.append(score)
    
    # シルエットスコアが最高の場合、そのクラスタ数とシルエットスコア、ラベル、シルエット値を保存
    if score > best_silhouette_score:
        best_n_clusters = n_clusters
        best_silhouette_score = score
        best_labels = labels
        best_silhouette_vals = silhouette_vals

# 最適なクラスタ数とその時のシルエットスコアを表示
print(f"The best number of clusters is {best_n_clusters} with a silhouette score of {best_silhouette_score}")

# シルエットスコアのプロット
plt.plot(n_clusters_candidates, silhouette_scores, 'o-')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score')
plt.grid(True)
plt.title('Silhouette scores for different numbers of clusters')
plt.show()

# 最適なクラスタ数でのクラスタリング結果を表示
for i in range(best_n_clusters):
    print(f"Cluster {i+1}:")  # クラスタ番号を1から始める
    print([company_names[ticker] for ticker, label in zip(returns.columns, best_labels) if label == i])

# 銘柄とクラスタラベルのデータフレームを作成
clusters_df = pd.DataFrame({'Ticker': returns.columns, 'Cluster': best_labels + 1}) 

# 銘柄名を追加
clusters_df['Company'] = clusters_df['Ticker'].apply(lambda x: company_names[x])

print(clusters_df)

出力結果（シルエット・スコア）

Cluster 1:
['Hitachi', 'Toyota', 'Honda', 'ITOCHU', 'Mitsubishi Corp', 'Mitsubishi Trading', 'MUFG', 'SMBC', 'Mizuho', 'Tokio Marine']
Cluster 2:
['ShinEtsu', 'Fanuc', 'Tokyo Electron']
Cluster 3:
['Recruit', 'SMC', 'Daikin', 'Nidec', 'Sony', 'Keyence', 'MuRata', 'HOYA', 'SoftBankG']
Cluster 4:
['Seven&I', 'Takeda', 'Astellas', 'DaiichiSankyo', 'Nintendo', 'NTT', 'KDDI', 'SoftBank']
Ticker Cluster Company
0 3382.T 4 Seven&I
1 4063.T 2 ShinEtsu
2 4502.T 4 Takeda
3 4503.T 4 Astellas
4 4568.T 4 DaiichiSankyo
5 6098.T 3 Recruit
6 6273.T 3 SMC
7 6367.T 3 Daikin
8 6501.T 1 Hitachi
9 6594.T 3 Nidec
10 6758.T 3 Sony
11 6861.T 3 Keyence
12 6954.T 2 Fanuc
13 6981.T 3 MuRata
14 7203.T 1 Toyota
15 7267.T 1 Honda
16 7741.T 3 HOYA
17 7974.T 4 Nintendo
18 8001.T 1 ITOCHU
19 8031.T 1 Mitsubishi Corp
20 8035.T 2 Tokyo Electron
21 8058.T 1 Mitsubishi Trading
22 8306.T 1 MUFG
23 8316.T 1 SMBC
24 8411.T 1 Mizuho
25 8766.T 1 Tokio Marine
26 9432.T 4 NTT
27 9433.T 4 KDDI
28 9434.T 4 SoftBank
29 9984.T 3 SoftBankG

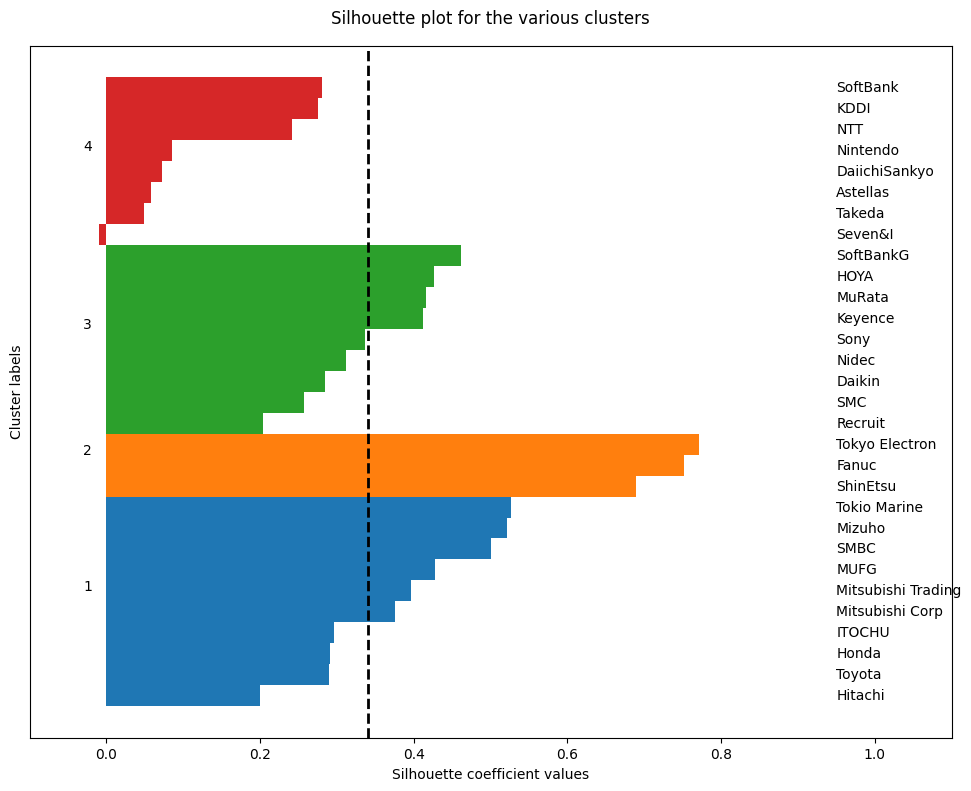
まあ、概ね順当な結果かなとは思うが、Cluster4がセブン＆アイ、製薬会社（武田薬品工業、アステラス製薬、第一三共）、任天堂、通信事業者（NTT,KDDI、ソフトバンク）で構成されているのはやや意外。

もう少し詳しく見るために、シルエット図を描いてみることにした。

# シルエット図のプロット
fig, ax = plt.subplots(1, 1, figsize=(10, 8))
y_lower, y_upper = 0, 0
yticks = []
for i, cluster in enumerate(np.unique(best_labels)):
    cluster_silhouette_vals = silhouette_vals[best_labels == cluster]
    cluster_silhouette_vals.sort()
    y_upper += len(cluster_silhouette_vals)
    ax.barh(range(y_lower, y_upper), cluster_silhouette_vals, edgecolor='none', height=1)
    ax.text(-0.03, (y_lower + y_upper) / 2, str(i + 1))
    y_lower += len(cluster_silhouette_vals)
    
    # 銘柄名の追加
    for j, ticker in enumerate(returns.columns[best_labels == cluster]):
        company_name = company_names[ticker]  # Tickerを会社名に変換
        ax.text(0.95, y_lower - len(cluster_silhouette_vals) + j, company_name, ha='left', va='center')  # テキストの位置を左に移動

# 平均シルエットスコアを縦線でプロット
avg_score = np.mean(best_silhouette_vals)
ax.axvline(avg_score, linestyle='--', linewidth=2, color='black')
ax.set_yticks([])
ax.set_xlim([-0.1, 1.1])  # x軸の範囲を少し広げて銘柄名を表示できるようにする
ax.set_xlabel('Silhouette coefficient values')
ax.set_ylabel('Cluster labels')
ax.set_title('Silhouette plot for the various clusters', y=1.02);

plt.tight_layout()
plt.show()

出力結果（シルエット図）

主成分分析

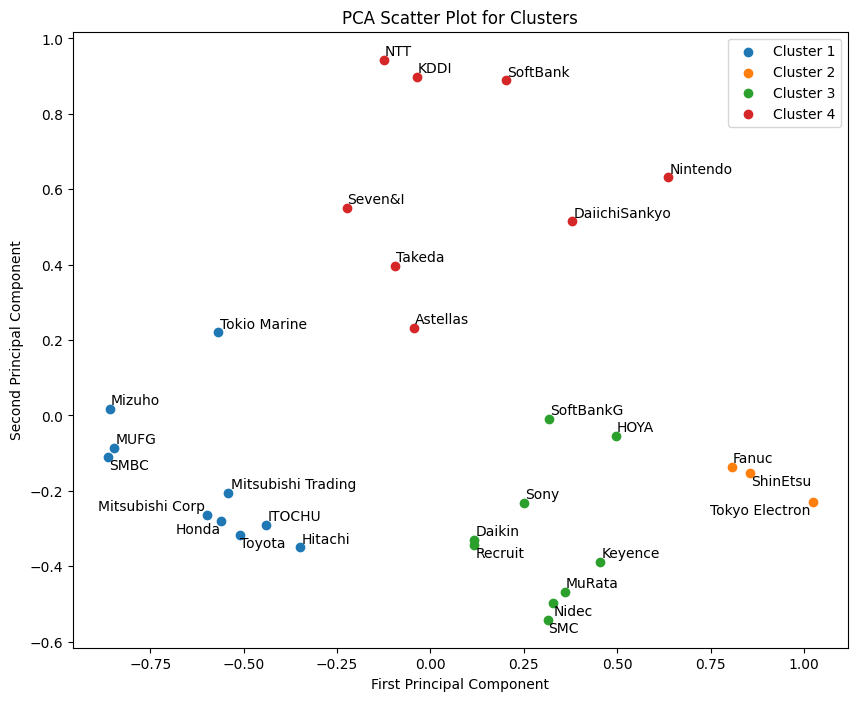
まだよくわからないので、主成分分析を使って次元削減して、2次元プロットしてみる。
図に描いたときに銘柄名が重なるのを避けるため、パッケージ（adjustText）を利用したいが、GoogleColabではプリインストールされていないので、ここでインストール。

pip install adjustText

そこで、主成分分析。

# パッケージの追加インポート
from adjustText import adjust_text
from sklearn.decomposition import PCA

# PCAのインスタンスを作成
pca = PCA(n_components=2)

# PCAを適用
pca_results = pca.fit_transform(returns.corr())

# プロット
plt.figure(figsize=(10,8))
texts = []  # テキストオブジェクトを保存するリスト
for i, cluster in enumerate(np.unique(best_labels)):
    plt.scatter(pca_results[best_labels == cluster, 0], pca_results[best_labels == cluster, 1], label=f'Cluster {i+1}')  # クラスタ番号を1から始める
    for j, ticker in enumerate(returns.columns[best_labels == cluster]):
        texts.append(plt.text(pca_results[best_labels == cluster][j, 0],  # テキストオブジェクトを追加
                              pca_results[best_labels == cluster][j, 1], 
                              company_names[ticker]))  # 会社名をプロット

# テキストラベルの位置を自動調整
adjust_text(texts)

plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA Scatter Plot for Clusters')
plt.legend()
plt.show()

出力結果

わかったようでわからない図だが、まあこれは主成分分析の常なんで仕方ないか。

おわりに

何をやってるか結局よくわからなくなったが、Yahoo Financeのデータも利用できたし、クラスタリング分析、さらに主成分分析までできたので、今回はこれで終了。