はじめに
『機械学習のエッセンス(http://isbn.sbcr.jp/93965/)』のPythonサンプルをJuliaで書き換えてみる。(第05章08k-Means法)の続きです。
PCAのアルゴリズム
ここは実装に出てくる最終的な式だけ書きます。詳細は本をご参照ください。
データ$\{x_i\}_{i=1}^n$の平均を$\overline{x}$とする。
\overline{x} = \frac{1}{n}\sum_{i=1}^n x_i
データ行列$X$のすべての行から$\overline{x}$を引いたものを$Y$とする。
Y =\begin{pmatrix}
(x_1 - \overline{x})^T\\
(x_2 - \overline{x})^T \\
\vdots \\
(x_n - \overline{x})^T
\end{pmatrix}
= (x_{ij} - \frac{1}{n}\sum_{k=1}^n x_{kj})
$X$の共分散行列$S$は次のように表される。
\begin{eqnarray}
S &=& \frac{1}{n}\sum_{i=1}^n(x_i - \overline{x})(x_i - \overline{x})^T \\
&=& \frac{1}{n}Y^TY
\end{eqnarray}
このとき$Y$の特異値分解を$U$, $\Sigma$, $V$とする。
$Y = U \Sigma V^T$なので次のようになる。
- 式05-27
\begin{eqnarray}
S &=& \frac{1}{n}Y^TY \\
&=& \frac{1}{n}(U \Sigma V^T)^T(U \Sigma V^T) \\
&=&
V\begin{pmatrix}
\sigma_1^2/n & & & \\
& \sigma_2^2/n & & \\
& & \ddots &\\
& & & \sigma_M^2/n
\end{pmatrix}V^T
\end{eqnarray}
これは共分散行列$S$の固有値が$\sigma_1^2/n,\sigma_2^2/n,\cdots,\sigma_M^2/n$であり、大きい順に並べたものとなっている。
SVDを計算する関数があればPCAの計算ができる。
アルゴリズム
- 共分散行列$S$を計算する。
- $S$を特異値分解し$S=U \Sigma V$とし、$V$の上から$c$行を取り出したものを$V^{(c)}$とする。
- 与えられたベクトル$x$に対して$V^{(c)}x$を計算する。
前提・補足
特異値分解のsvdsについて
本のPythonの実装ではscipyライブラリのscipy.sparse.linalg.svdsを使っています。
https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.linalg.svds.html
これは特異値分解のメソッドで、オプションkを指定すると、特異値の上位k個だけ計算することができるようです。
今回のPCAの実装で特徴量(11次元)を2次元に圧縮するためにこのメソッドが使われています。
Juliaで同じような関数を調べたのですが見つかりませんでした。(特異値分解のsvd関数はLinearAlgebraにありますが、上記のようなオプションがありません。)
同じことが出来るパッケージがないか調べたところPROPACK.jlというものを見つけました。
https://github.com/JuliaSmoothOptimizers/PROPACK.jl
しかし、マニュアルにある下記のコマンドを実行したところPkg.test("PROPACK")でエラーになってしまいました。
julia> Pkg.clone("https://github.com/JuliaSmoothOptimizers/PROPACK.jl.git")
julia> Pkg.build("PROPACK")
julia> Pkg.test("PROPACK")
そのまま無理矢理使おうとしてみましたが、エラーが出て使うことが出来ませんでした。(まだJuliaの今のバージョン(1.1.0)に対応していないのかもしれません。エラーについて詳しくは調べていません。)
ここは今回の実装のキモになる部分だと思うので困っていたのですが、JuliaはPythonのライブラリが使用できることを思い出しました。
この記事の目的がPythonサンプルのJuliaへの置き換えだったので、出来ればJuliaのみで完結させたかったのですが最後の最後でPythonパッケージを呼び出すという方法になってしまいました。
JuliaからPythonのライブラリを使用する
JuliaにはPyCall.jlというPythonのfunctionを呼べるライブラリがあります。
https://github.com/JuliaPy/PyCall.jl
これを使います。
準備
PyCallパッケージのインストール
julia> using Pkg
julia> Pkg.add("PyCall")
(略)
PyCallは.juliaディレクトリ配下に別途インストールされるようで、予めPythonをインストールする必要はなさそうです。(ただし全くPythonが入っていない環境では試していません。)
- Pythonのバージョンを確認してみます。
julia> using PyCall
(略)
julia> PyCall.pyversion
v"3.7.2"
scipyパッケージのインストール
PyCallで使うPythonにscipyパッケージをインストールします。
julia> pyimport_conda("scipy", "scipy")
[ Info: Installing scipy via the Conda scipy package...
[ Info: Running `conda install -y scipy` in root environment
(略)
実装
module pca
using Random
using Statistics
using PyCall
mutable struct PCA
n_components
tol
rng_::MersenneTwister
VT_
function PCA(n_components)
rng = MersenneTwister(0)
new(n_components, 0.0, rng)
end
end
function fit(obj::PCA, X)
v0 = randn(obj.rng_, minimum(size(X)))
xbar = mean(X, dims=1)
Y = X .- xbar
S = Y' * Y
linalg = pyimport("scipy.sparse.linalg")
U, Σ, VT = linalg.svds(S, k=obj.n_components, tol=obj.tol, v0=v0)
obj.VT_ = VT[end:-1:1, :]
end
function transform(obj::PCA, X)
(obj.VT_ * X')'
end
end
第05章02回帰
のところで使ったワインの品質データを使います。
include("./pca.jl")
using .pca
using CSV
using Plots
dataframe = CSV.read("winequality-red.csv", header=true, delim=';')
row,col=size(dataframe)
Xy = Float64[dataframe[r,c] for r in 1:row, c in 1:col]
X = Xy[:, 1:end-1]
model = pca.PCA(2)
pca.fit(model, X)
Y = pca.transform(model, X)
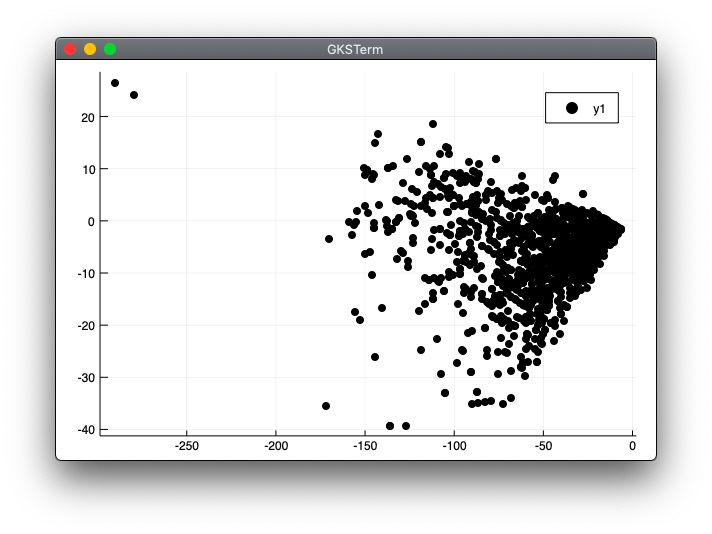
scatter(Y[:,1], Y[:,2], color=:black)
実行結果
julia> include("pca_test1.jl")
補足(ランダム値から生成するv0をPythonサンプルの値で試す)
実行結果の図が本の結果と少し異なったため、ランダム値を利用している所にPythonサンプルでの値を埋め込んで試してみました。
(略)
# v0 = randn(obj.rng_, minimum(size(X)))
v0 = [1.76405235, 0.40015721, 0.97873798, 2.2408932, 1.86755799,
-0.97727788, 0.95008842, -0.15135721, -0.10321885, 0.4105985,
0.14404357
(略)
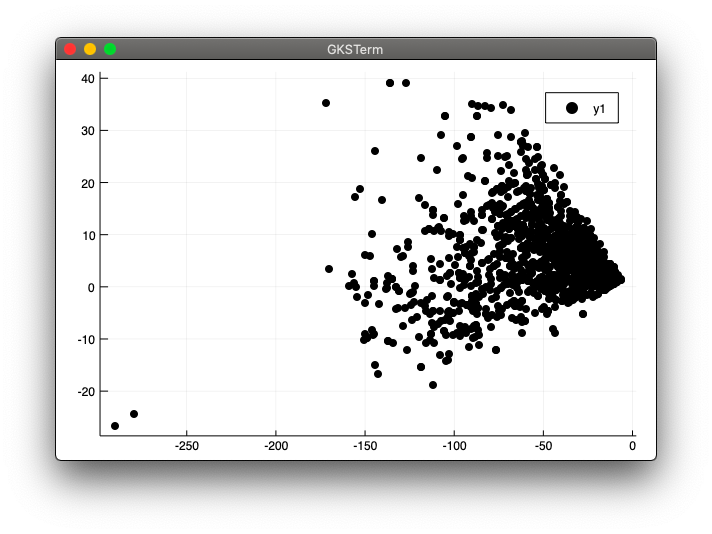
実行結果
julia> include("pca_test1.jl")
本とほぼ同じ図が得られました。