『機械学習のエッセンス(http://isbn.sbcr.jp/93965/)』のPythonサンプルをJuliaで書き換えてみる。（第05章02回帰）

はじめに

『機械学習のエッセンス(http://isbn.sbcr.jp/93965/)』のPythonサンプルをJuliaで書き換えてみる。（第04章09統計）の続きです。

「第05章01準備」は「インターフェース」の部分に少しコードがありますが、擬似的なものだったので書き換えは省略しました

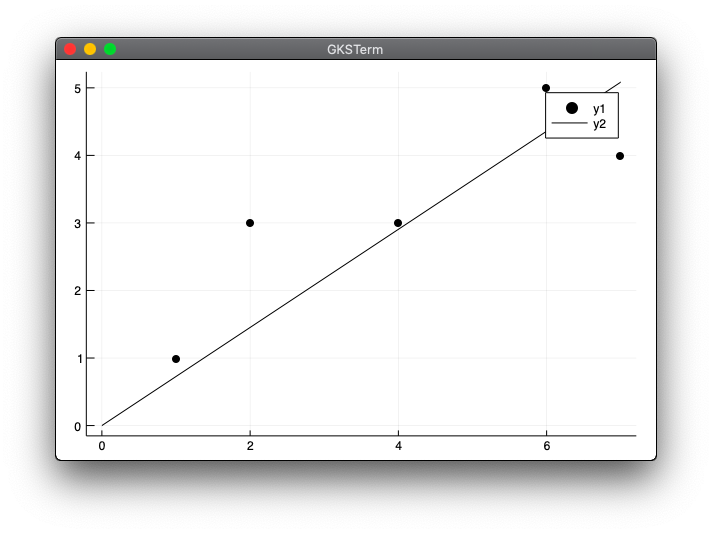
原点を通る直線による近似

x = (x_1,\cdots, x_n)^T, \ y = (y_1,\cdots,y_n)^T

$x$：特徴量、$y$：ターゲット

E = \sum_{i=1}^n(ax_i - y_i)^2 \\
a = \frac{x^Ty}{\|x\|^2}

reg1dim1.jl

using LinearAlgebra
using Plots

reg1dim1(x, y) = dot(x, y) / sum(x.^2)

x = [1, 2, 4, 6, 7]
y = [1, 3, 3, 5, 4]
a = reg1dim1(x, y)

xmax = maximum(x)

scatter(x, y, color="black")
plot!([0, xmax], [0, a*xmax], color="black")

実行結果

julia> include("reg1dim1.jl")

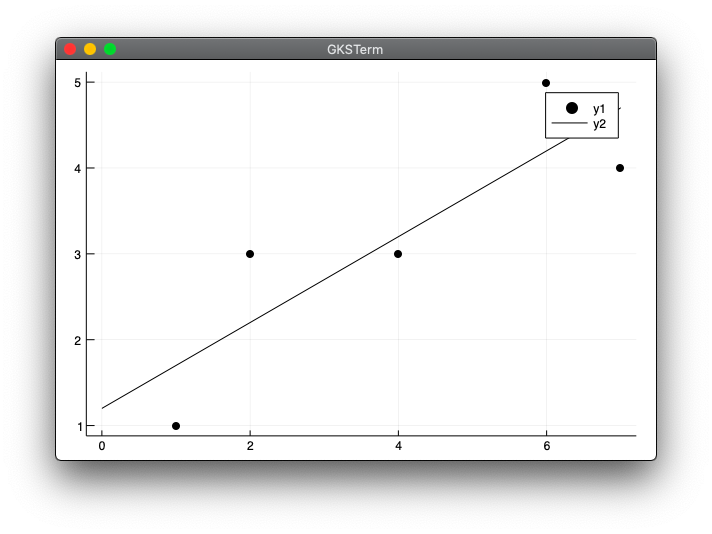
一般の直線による近似

E = \sum_{i=1}^n(ax_i + b - y_i)^2 \\
a = \frac{\sum_{i=1}^n x_i y_i - \frac{1}{n}\sum_{i=1}^n x_i \sum_{i=1}^n y_i}{\sum_{i=1}^n {x_i}^2 - \frac{1}{n} (\sum_{i=1}^n x_i)^2} \\
b = \frac{1}{n}\sum_{i=1}^n(y_i - ax_i)

reg1dim2.jl

using LinearAlgebra
using Plots

function reg1dim2(x, y)
  n = length(x)
  a = (dot(x, y) - sum(y) * sum(x) / n ) / (sum(x.^2) - (sum(x)^2) / n)
  b = (sum(y) -  a * sum(x)) / n
  return a, b
end

x = [1, 2, 4, 6, 7]
y = [1, 3, 3, 5, 4]
a, b = reg1dim2(x, y)

xmax = maximum(x)

scatter(x, y, color="black")
plot!([0, xmax], [b, a*xmax + b], color="black")

実行結果

julia> include("reg1dim2.jl")

特徴量ベクトルが多次元の場合

プログラムだけだと内容が不明になるので一部本の解説を書きますが、定義と結果のみで計算途中は省略します。

y = w_0 + w_1x_1 + w_2x_2 + \cdots w_dx_d + \varepsilon

$(x_0,\cdots,x_d)^T$は入力変数、$w_0, w_1, \cdots, w_d$はパラメータ、$y$はターゲット、$\varepsilon$はノイズ。

ベクトル$x=(x_1,x_2,\cdots,x_d)^T$に対して要素1を付加したベクトル$\tilde{x}$、ベクトル$w=(w_0,w_1,\cdots,w_d)^T$とすると、

y = w^T\tilde{x}

行列$X$について、左に1列追加してその要素をすべて１としたものを$\tilde{X}$とする。

\hat{y}(w) = \tilde{X}w 

ターゲット$y$との差の2乗の和$||y - \hat{y}(w)||^2$を最小化することを考える。

w = (\tilde{X}^T\tilde{X})^{-1}\tilde{X}^Ty

まず計算のみ実装

linearreg.jl

module linearreg

mutable struct LinearRegression
  w_
  function LinearRegression()
    new(Nothing)
  end
end

function fit(s::LinearRegression, X, t)
  Xtil = hcat(ones(size(X)[1]), X)
  A = Xtil' * Xtil
  b = Xtil' * t
  s.w_ = A \ b
end

function predict(s::LinearRegression, X)
  if ndims(X) == 1
    X = reshape(X, 1, :)
  end
  Xtil = hcat(ones(size(X)[1]), X)
  return Xtil * s.w_
end

end

reg_test1.jl

using .linearreg
using Random

n = 100
scale = 10
Random.seed!(0)
X = rand(n, 2) .* scale
w0 = 1
w1 = 2
w2 = 3
y = w0 .+ w1 * X[:, 1] .+ w2 * X[:, 2] .+ randn(n)

model = linearreg.LinearRegression()
linearreg.fit(model, X, y)
println("係数:", model.w_)
println("(1, 1)に対する予測値:", linearreg.predict(model, [1,1]))

実行結果

julia> include("linearreg.jl")
Main.linearreg

julia> include("reg_test1.jl")
係数:[0.812652, 1.99266, 3.01417]
(1, 1)に対する予測値:[5.81949]

本の「(1, 1)に対する予測値」の結果は6.07483080617となっています。P.290から一部引用すると、

(1,1)に対する真の値は$1 + 2 \times 1 + 3 \times 1 = 6$なので、それなりによい予測がされているように見えます。

とあります。5.81949がそれなりによい予測なのかよくわかりません。乱数を使用しているので本と答え合わせが出来ず、ロジックが間違っている可能性があります。
ここでreg_test1.jlファイルのnの値を100から1000に変更して試してみます。

（一部抜粋）reg_test1.jl

n = 1000

実行結果

julia> include("reg_test1.jl")
係数:[1.04535, 1.9861, 3.00733]
(1, 1)に対する予測値:[6.03878]

6に近づきました。ちょっと自信がないですが、とりあえずロジックは合っているものとして進めてみます。

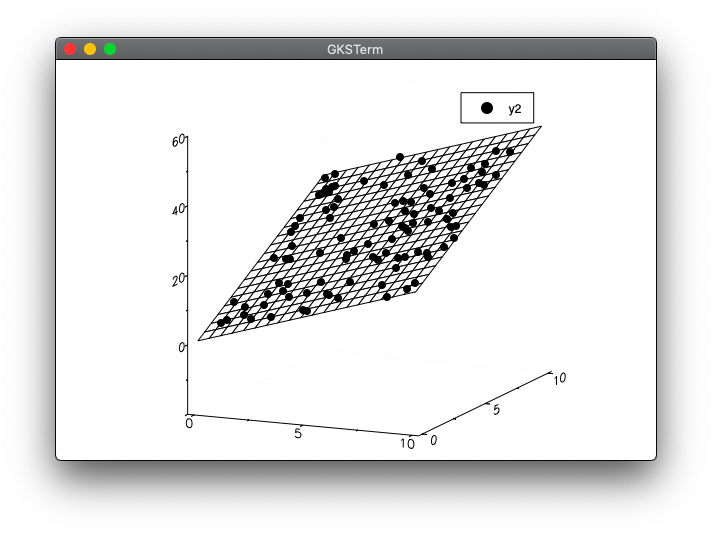
グラフを追加

reg_test1.jl

using .linearreg
using Random
using Plots

n = 100
scale = 10
Random.seed!(0)
X = rand(n, 2) .* scale
w0 = 1
w1 = 2
w2 = 3
y = w0 .+ w1 * X[:, 1] .+ w2 * X[:, 2] .+ randn(n)

model = linearreg.LinearRegression()
linearreg.fit(model, X, y)
println("係数:", model.w_)
println("(1, 1)に対する予測値:", linearreg.predict(model, [1,1]))

x_range = LinRange(0, scale, 20)
y_range = LinRange(0, scale, 20)
xmesh = repeat(x_range', outer=(length(y_range),1))
ymesh = repeat(y_range,  outer=(1,length(x_range)))
zmesh = reshape(model.w_[1] .+ model.w_[2] .* vec(xmesh) .+ model.w_[3] .* vec(ymesh), size(xmesh))

plot(x_range, y_range, zmesh, color="red", st=:wireframe)
scatter!(X[:,1], X[:,2], y, color="black")

実行結果

julia> include("reg_test1.jl")
係数:[0.812652, 1.99266, 3.01417]
(1, 1)に対する予測値:[5.81949]

• ワイヤーフレーム部分をredにしてしているのですが赤くなりませんでした。いろいろオプションを調べたのですが分からず・・・。
• 最後のscatterをplotの前にもってくるとワイヤーフレーム部分がドットの上に来てしまい、ドットが見えなくなりました。
• 本の場合、グラフがドラッグすることで回転できるようですが、PlotのデフォルトであるGRでは固定でした。他の描画を利用するとできるかもしれません。（試していません）

実践的な例

本と同じく、下記のデータを取得し、プログラムと同じディレクトリに置きます。
https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv

CSVパッケージのインストール

JuliaでCSVファイルを読み込むため、CSVパッケージをインストールします。

julia> using Pkg

julia> Pkg.add("CSV")

• RMSE

予測値

\hat{y}=(\hat{y}_1,\hat{y}_2,\cdots,\hat{y}_n)

と正解値（出力訓練データ）

y = (y_1,y_2,\cdots,y_n)

について

\sqrt{\sum_{i=1}^n(\hat{y}_i-y_i)^2} = ||\hat{y} - y||

reg_winequality.jl

using .linearreg
using CSV
using Random
using Statistics
using Printf

dataframe = CSV.read("winequality-red.csv", header=true, delim=';')
row,col=size(dataframe)

Xy = Float64[dataframe[r,c] for r in 1:row, c in 1:col]

Random.seed!(0)
shuffle(Xy)

train_X = Xy[1:row-1000, 1:col-1]
train_y = Xy[1:row-1000, col-1]
test_X = Xy[row-999:row, 1:col-1]
test_y = Xy[row-999:row, col-1]

model = linearreg.LinearRegression()
linearreg.fit(model, train_X, train_y)

y = linearreg.predict(model, test_X)

println("最初の5つの正解と予測値:")
for i in 1:5
  println("$(@sprintf("%1.0f", test_y[i])) $(@sprintf("%5.3f",y[i]))")
end
println()
println("RMSE:", mean(sqrt.((test_y .- y ).^2)))

スライスについて補足

（一部抜粋）reg_winequality.jl

train_X = Xy[1:row-1000, 1:col-1]
train_y = Xy[1:row-1000, col-1]
test_X = Xy[row-999:row, 1:col-1]
test_y = Xy[row-999:row, col-1]

この部分は一応、Pythonのコードで配列の形式を確認しました。Xyは(1599,12)で、上記はそれぞれ下記の形式になっています。

(599, 11)
(599,)
(1000, 11)
(1000, )

実行結果

julia> include("linearreg.jl")
Main.linearreg

julia> include("reg_winequality.jl")
最初の5つの正解と予測値:
9 9.300
10 10.000
9 9.000
9 9.300
9 9.000

RMSE:1.4790872526759814e-11

なんか、本と数値が大分違う気がしました。ただし、最初の5つの数値が一致しないのはshuffle関数でXyをシャッフルしているせいだと思います。また、RMSEは本では約0.67となっていて、一部引用すると

平均として1以上ずれていないということで、ここではまあままの意味のある予測はできている程度に思ってください

とあります。
今回実行した結果も約1.48なのでまあまあと見なすことにしました。いろいろ調べたのですがRMSEの目安についてはなかなか難しそうです。

補足

第4章までは本と答え合わせができたのですが、ここでは乱数を利用するので本と違う結果になってしまいます。ロジックが間違っていないか、なんどもプログラムを見直しました。合っていると思うのですが、間違っていたらすみません。