目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
| リンク | 説明 |
|---|---|
| marubatsu.py | Marubatsu、Marubatsu_GUI クラスの定義 |
| ai.py | AI に関する関数 |
| test.py | テストに関する関数 |
| util.py | ユーティリティ関数の定義。現在は gui_play のみ定義されている |
| tree.py | ゲーム木に関する Node、Mbtree クラスの定義 |
| gui.py | GUI に関する処理を行う基底クラスとなる GUI クラスの定義 |
AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。
ミニマックス法の問題点
前回の記事で、ミニマックス法を使って特定のノードの評価値を動的に計算する方法を紹介しましたが、その際にルートノードの評価値を計算するためには、50 万以上もある 〇×ゲームの ゲーム木のノードの評価値をすべて計算する必要がある ため、評価値の計算に約 30 秒も時間がかかる という問題があります。
この問題を解決する方法として、前回の記事で説明した、探索空間を狭める という方法があります。具体的には、ミニマックス法で評価値を計算する際に、何らかの方法で計算を行うノードの数を減らす というものです。ミニマックス法を行う際に 計算するノードを減らした上 で、ミニマックス法と同じ 最適解を得る ことができる αβ(アルファベータ)法 というアルゴリズムがあるので、今回の記事ではその説明を行います。
αβ 法の仕組み
αβ 法は 直観的にわかりづらく、αβ法を実装する プログラムもわかりづらい ので、本記事ではその仕組みを説明し、順を追ってプログラムを実装することにします。
ミニマックス法では、〇×ゲームのゲーム木に対して、下記のような計算を行います。
- 〇 の手番のノードの評価値として、子ノードの評価値の最大値を計算する
- × の手番のノードの評価値として、子ノードの評価値の最小値を計算する
ゲーム木の ノードのうち、子ノードの評価値の 最大値を計算 するノードのことを max ノード、最小値を計算 するノードのことを min ノード と呼びます。
ゲーム木のノードは、必ず max ノードと min ノードのいずれかに分類 され、ゲーム木の深さ によって max ノードと min ノードが交互に現れる という性質があります。
子ノードの評価値の計算の性質を利用した枝狩り
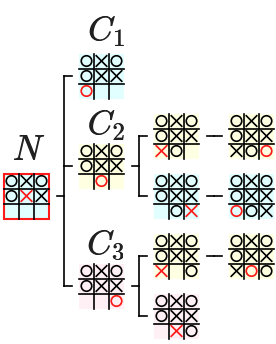
具体例として、下図の赤枠の 〇 の手番の局面である max ノードの評価値を計算する場合 について説明します。以後はこの赤枠のノードのことを $N$ と表記することにします。また、$N$ の 3 つの子(child)ノードを上から順に $C_1$、$C_2$、$C_3$ と表記することにします。
ミニマックス法では、max ノード の 子ノードの評価値 を順番に計算し、その 最大値を求める 処理を行うので、最初に $N$ の最初の子ノードの $C_1$ の評価値を計算します。
下図の赤枠の $C_1$ のノードは 〇 が勝利している局面なので、評価値が 1 として計算 され、下図のようになります。以後の図では、直前に処理を行ったノードの枠を赤色 で、評価値が計算されていないノードを暗く表示 することにします。
次に、下図の赤枠の $C_2$ の評価値を計算する必要がありますが、$C_2$ には 2 つの子ノードが存在する ので、それらの評価値を計算する必要があります。$C_2$ の 2 つの子ノードは $N$ の孫(grandchild)ノードなので、$G_{21}$、$G_{22}$ と表記することにします。
下図の赤枠の $G_{21}$ には 1 つだけ子ノードが存在し、その 子ノード は引き分けなので 評価値は 0 となります。子ノードが 1 つしか存在しない場合は、max ノードでも min ノードでも子ノードの評価値を計算すればよいので、$G_{21}$ の 評価値は下図のように 0 になります。
実は、この時点で次の $G_{22}$ の 評価値を計算する必要がない ことが 確定 します。その理由について少し考えてみて下さい。
min ノードでの枝狩り(α 狩り)
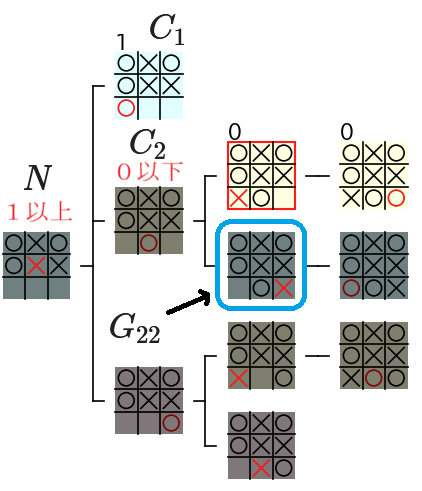
$C_2$ は × の手番 なので、子ノードの評価値の最小値を計算する min ノード です。従って、上図のように $C_2$ の子ノードである $G_{21}$ の 評価値が 0 と計算された時点 で $G_{22}$ の 評価値を計算しなくても $C_2$ の 評価値 は下図のように 0 以下 であることが 確定 します。
なお、下図では $C_2$ は 2 つしか子ノードを持ちませんが、$C_2$ が 3 つ以上 の子ノードを持つ場合でも、$G_{21}$ の 評価値が 0 と計算された時点 で残りの子ノードの評価値の値に関わらず $C_2$ の 評価値 が 0 以下 であることが 確定 します。
また、$C_2$ の親ノードである $N$ は子ノードの評価値の最大値を計算する max ノード なので、$C_1$ の 評価値が 1 と計算された時点 で、下図のように $N$ の 評価値は 1 以上 であることが 確定 します。
これらのことから、下図の青枠の $G_{22}$ の 評価値がどのような値であっても 親ノードの $C_2$ の 評価値は 0 以下 になり、$N$ の 評価値に影響を与えることはありません。従って、$C_2$ の 残りの子ノード である $G_{22}$ 及び その子孫ノード の評価値を 計算する必要はありません。
上記から、min ノードの評価値を計算 する際に、以下の性質があることがわかります。
- それまでに計算された 兄弟ノード の 評価値の最大値を α とする
- 子ノードの中 で、α 以下の評価値が計算された時点 で評価値が α 以下になることが確定 するため、そのノードの評価値 が max ノードである 親ノードの評価値に影響を与えないことが確定 する
- 従って、その時点で 残りの子ノードの評価値を計算する必要がないことが確定 する
以前の記事で説明したように、木構造 のデータを 探索する際 に、探索を行う必要がない ノードとその子孫ノードの探索を行わない ようにすることを、枝狩り(pruning)と呼ぶと説明しました。枝狩りは 探索空間を狭める 処理です。
αβ 法 では、上記の手順で min ノードの子ノードの枝狩り を行い、その際に上記の α という値 を用いて枝狩りを行うので、この枝狩りのことを α 狩り(alpha pruning)や α カット などと呼びます。また、α の値 のことを α 値 と呼びます。
α 狩りの手順をまとめると以下のようになります。
αβ 法では、以下の手順で min ノード の 子孫ノード に対する α 狩り を行う。
- それまでに計算された 兄弟ノード の 評価値の最大値を α とする
- 子ノードの中 で α 以下 の評価値が 計算された時点 で 残りの子ノードの評価値の計算を省略 する
max ノードでの枝狩り(β 狩り)
ゲーム木 では、深さごとに max ノードと min ノードが交互 に現れます。また、max ノードと min ノードの性質は 正反対の性質 なので、max ノード においても、min ノードと同様の考え方 で 枝狩りを行う ことができます。
具体的には、max ノード の評価値を計算 する際に以下の性質があります。min ノードとの違い は下記の太字で表記した 最大値が最小値 に、以下が以上 に、α が β に、max が min になった点だけです。
- それまでに計算された兄弟ノードの評価値の 最小値を β とする
- 子ノードの中で、β 以上 の評価値が計算された時点で評価値が β 以上 になることが確定するため、そのノードの評価値が min ノード である親ノードの評価値に影響を与えないことが確定する
- 従って、その時点で残りの子ノードの評価値を計算する必要がないことが確定する
αβ 法 では、上記の手順で max ノードの子ノードの枝狩り を行い、その際に上記の β という値 を用いて枝狩りを行うので、その枝狩りのことを β 狩り(beta pruning)や β カット などと呼びます。また、β の値 のことを β値 と呼びます。
β 狩りの手順をまとめると以下のようになります。
αβ 法では、以下の手順で max ノード の 子孫ノード に対する β 狩り を行う。
- それまでに計算された 兄弟ノード の 評価値の最小値を β とする
- 子ノードの中 で β 以上 の評価値が 計算された時点 で 残りの子ノードの評価値の計算を省略 する
祖先ノードを考慮した min ノードでの α 狩り
上記では、兄弟ノードの評価値を利用した枝狩りを行いましたが、αβ 法では 祖先ノード で計算されている 評価値を利用 することで、さらなる枝狩り を行うことができます。
その方法は、先ほどと同様に min ノードと max ノードで異なる ので、順に説明します。
min ノードでは、以下の方法で α 狩りを行うことができます。
- 祖先ノード の中の max ノード をすべて探す
- 探した max ノードの中で、評価値が計算済 の 子ノードの評価値の最大値を α とする
- 子ノードの中で α 以下 の評価値が 計算された時点 で 残りの子ノードの評価値の計算を省略 する
先程との違い は、α 値 を「親ノード の子ノード(兄弟ノード)で計算された評価値の最大値」で計算していたのを、「祖先ノードの中のすべての max ノード の子ノードで計算された評価値の最大値」で計算するようにした点です。親ノード は 祖先ノードの一種 なので、α 値を計算する範囲 を親ノードから 祖先ノードに広げた アルゴリズムです。
α 狩りの計算の具体例
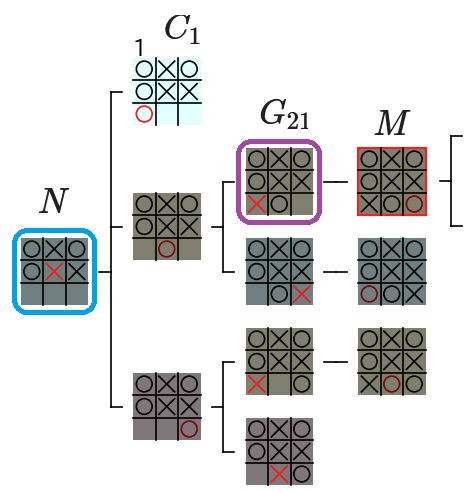
具体例として、先程の例と同じようなゲーム木での評価値の計算を説明します。なお、実際の 〇×ゲームのゲーム木では、下図の赤枠のノードは決着がついた局面なので子ノードは存在しませんが、下図のようにこのノードが 決着がついておらず、子ノードが存在する場合 の 評価値の計算の処理 を考えてみることにします。以後は赤枠のノードを min ノードであることから $M$ と表記します
上図の $M$ は min ノード です。また、$M$ の 祖先ノード の中で、max ノード は下図の 青枠の $N$ と 紫枠の $G_{21}$ です。$N$ と $G_{21}$ の 子ノード の中で 評価値が計算されている のは $C_1$ だけ なので、α は 1 と計算されます。
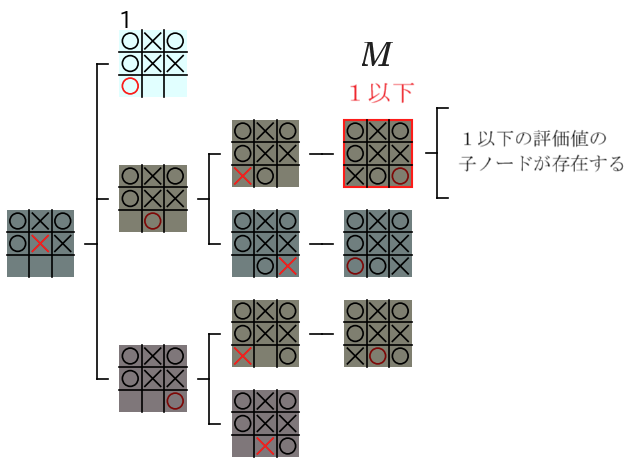
$M$ の 子ノードの中 で、1 以下 の評価値が 計算された時点 で、$M$ の 残りの子ノード の評価値を 計算する必要がないことが確定 します。その理由について少し考えてみて下さい。
$M$ は min ノード なので、子ノードの中に 1 以下の評価値が存在 した場合は、$M$ の 評価値 は下図のように 1 以下 になります。
上図の $M$ の 親ノード である $G_{21}$ は、max ノード です。上図の $G_{21}$ には子ノードは 1 つしか存在しませんが、一般的な評価値の計算例になるように、下図のように $G_{21}$ に 複数の子ノードが存在する場合 のことを考えます。
$G_{21}$ に 複数の子ノードが存在 する場合は、下記の 2 種類の状況が考えられます。
- $G_{21}$ の $M$ 以外の子ノードに 評価値が 1 より大きい ノードが 存在する
- $G_{21}$ の $M$ 以外の子ノードに 評価値が 1 より大きい ノードが 存在しない
上記の両方の場合 で先程の方法で α 狩りを行うことができる ことを 示すことで、常に 先ほどの方法で α 狩りを行うことができる ことが 証明できます。
子ノードに評価値が 1 より大きいノードが存在する場合
$G_{21}$ は max ノード なので、$G_{21}$ の子ノードの中に下図のように 1 より大きい評価値の子ノードが存在 する場合は、$G_{21}$ の 評価値は 1 より大きな値 となります。
この場合は $M$ の評価値は $G_{21}$ の評価値に 影響を及ぼしません。ミニマックス法では、子ノードの評価値 を元に 親ノードの評価値を計算する手法な ので、$G_{21}$ の評価値に影響を与えないということは、その 祖先の $N$ の評価値にも影響を与えない ことになります。従って、$M$ の 子ノード の中で 1 つでも 1 以下の評価値が計算された時点 で残りの子ノードの評価値を 計算しなくても良い ことが確認できました。
子ノードに評価値が 1 より大きいノードが存在しない場合
$G_{21}$ の子ノードの中に 1 より大きい評価値が 存在しない場合 は、以下の手順で計算が行われて下図のように $G_{21}$ と $C_2$ の評価値が計算されます。
- $G_{21}$ の全ての子ノードの評価値が 1 以下なので $G_{21}$ の 評価値は 1 以下 となる
- $G_{21}$ の 親ノード である $C_2$ は min ノード なので $C_2$の 評価値は 1 以下 となる
上記から、以下の理由で $M$ の 子ノード の中で 1 つでも 1 以下の評価値が計算された時点 で残りの子ノードの評価値を 計算しなくても良い ことが確認できます。
- $C_2$ の 親ノード である $N$ は max ノード で、$N$ には 評価値が 1 の子ノード $C_1$ が 存在する ので、$C_2$ の評価値は $N$ の 評価値に影響を及ぼさない
- 従って、$C_2$ の評価値を計算する際に必要となる、$C_2$ の 子孫ノードの評価値 はいずれも $N$ の 評価値に影響を及ぼさない
$G_{21}$ の 他の子ノードの評価値の値に関わらず、先程の α 狩りの手順が正しい ことが確認できたので、全ての場合で先程の α 狩りの手順が正しいことが証明できました。
祖先ノードを考慮した αβ 法
上記の例では、min ノード である $N$ の親ノードと、曾祖父ノードに max ノードが存在した場合の例ですが、もっと遠い祖先ノードに max ノードが存在する場合も同様 です。
また、max ノード でも 同様の方法で β 狩り を行うことができます。
以下は、祖先ノードを考慮した αβ 法 のアルゴリズムで、一般的にはこのアルゴリズムを αβ 法と呼びます。
αβ 法は、ミニマックス法で評価値を計算する際 に、下記の手順で α 狩り と β 狩り を行うアルゴリズムである。また、αβ 法 で求められる評価値は、ミニマックス法 で求められる評価値と 常に同じ になるので、最適解 の評価値を ミニマックス法より短い時間 で 求めることができる。
-
min ノード では、下記の手順で α 狩り を行う
- 祖先ノード の中の max ノード をすべて探す
- 探した max ノードの中で、評価値が計算済 の 子ノードの評価値の最大値を α とする
- 子ノードの中で α 以下 の評価値が 計算された時点 で 残りの子ノードの評価値の計算を省略 する
-
max ノード では、下記の手順で β 狩り を行う
- 祖先ノード の中の min ノード をすべて探す
- 探した min ノードの中で、評価値が計算済 の 子ノードの評価値の最小値を β とする
- 子ノードの中で β 以上 の評価値が 計算された時点 で 残りの子ノードの評価値の計算を省略 する
α 値と β 値の意味
αβ 法で行う枝狩りは、評価値を計算しても、最終的に計算する評価値 に 影響を及ぼさない ノードに対して行います。このことから α 値と β 値 は、ミニマックス法でそれぞれのノードの評価値を計算する際に、そのノードの評価値が 最終的に求める評価値 に 影響を与える可能性がない ことを表す 子ノードの評価値の範囲 と考えることができます。
αβ 法が行っているのは、探索の途中 で 絶対に探索する必要がないことが判明したノードの枝狩り であり、α 値と β 値 は枝狩りを行う 評価値の範囲を表す値 である。
αβ 法の実装
αβ 法のアルゴリズムがわかったので、αβ 法 に従ってゲーム木のノードの 評価値を動的に計算 する ai_abs1 を定義する事にします。αβ 法の 基本はミニマックス法 なので、まずは ai_mmdfs と 同じ処理を行う関数 として下記のプログラムのように ai_abs を定義 します。なお、ai_mmdfs との違いは、関数の名前 と、中で定義する ローカル関数の名前を ab_search とした点です。また、@ai_by_score のデコレーター式を記述すると、ai_abs の処理の確認が行いづらくなってしまうので、デコレーター式は現時点では削除しました。
from marubatsu import Marubatsu
from ai import dprint
from copy import deepcopy
def ai_abs(mb, debug=False):
count = 0
def ab_search(mborig):
nonlocal count
count += 1
if mborig.status == Marubatsu.CIRCLE:
return 1
elif mborig.status == Marubatsu.CROSS:
return -1
elif mborig.status == Marubatsu.DRAW:
return 0
legal_moves = mborig.calc_legal_moves()
score_list = []
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score_list.append(ab_search(mb))
if mborig.turn == Marubatsu.CIRCLE:
return max(score_list)
else:
return min(score_list)
score = ab_search(mb)
dprint(debug, "count =", count)
if mb.turn == Marubatsu.CIRCLE:
score *= -1
return score
修正箇所
from marubatsu import Marubatsu
from ai import dprint
from copy import deepcopy
-@ai_by_score
-def ai_mmdfs(mb, debug=False):
+def ai_abs(mb, debug=False):
count = 0
- def mm_search(mborig):
+ def ab_search(mborig):
nonlocal count
count += 1
if mborig.status == Marubatsu.CIRCLE:
return 1
elif mborig.status == Marubatsu.CROSS:
return -1
elif mborig.status == Marubatsu.DRAW:
return 0
legal_moves = mborig.calc_legal_moves()
score_list = []
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
- score_list.append(mm_search(mb))
+ score_list.append(ab_search(mb))
if mborig.turn == Marubatsu.CIRCLE:
return max(score_list)
else:
return min(score_list)
- score = mm_search(mb)
+ score = ab_search(mb)
dprint(debug, "count =", count)
if mb.turn == Marubatsu.CIRCLE:
score *= -1
return score
兄弟ノード評価値のみを考慮した α 狩りと β 狩りの実装
いきなり祖先ノードの評価値を考慮した αβ 法の実装を行うのは大変なので、本記事の最初に説明した、兄弟ノードの評価値のみを考慮 した下記の処理を実装することにします。
以下の手順で min ノードの子孫ノードの α 狩りを行う。
- それまでに計算された兄弟ノードの評価値の最大値を α とする
- 子ノードの中で α 以下の評価値が計算された時点で残りの子ノードの計算を終了する
以下の手順で max ノードの子孫ノードの β 狩りを行う。
- それまでに計算された兄弟ノードの評価値の最小値を β とする
- 子ノードの中で β 以上の評価値が計算された時点で残りの子ノードの計算を終了する
α 値と β 値の計算処理の実装
まず、上記の処理の中の α 値と β 値 を計算する処理 を実装します。上記では、α 値 を min ノードの 兄弟ノード の評価値の最大値と表記しましたが、min ノードの 兄弟ノードの評価値 を順番に 計算する処理を行う のは、min ノードの 親ノードである max ノード です。
従って、α 値を利用 して枝狩りを行うのは min ノード ですが、その α 値を計算 するのはその 親ノードである max ノード です。
同様に、β 値を利用 して枝狩りを行うのは max ノード ですが、その β 値を計算 するのはその 親ノードである min ノード です。
このように、α 値と β 値 は、その値を 計算するノード とその値を 利用するノード が 異なる 点がわかりづらく、間違えやすい ので注意が必要です。
ai_mmdfs では下記のプログラムのように、子ノードの評価値 を score_list という list の要素に記録し、すべての子ノードの評価値を計算した後 で max または min 関数でその最大値または最小値を まとめて計算 していました。
score_list = []
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score_list.append(ab_search(mb))
if mborig.turn == Marubatsu.CIRCLE:
return max(score_list)
else:
return min(score_list)
αβ 法では 子ノードの評価値を順番に計算する際 に、それまでの子ノードの評価値の最大値(または最小値)を 計算しておく 必要があるので、まとめて計算 することは できません。
そのため、下記のプログラムのように ai_abs を修正する必要があります。
- 4 行目の前で行っている、決着がついた局面の評価値の計算 では枝狩りを行うことはできないので、
ai_mmdfsから修正する必要はない - 5 ~ 12 行目:〇 の手番の max ノード の場合の処理を行う
-
6 行目:max ノード では、子ノードの評価値の 最大値 である α 値を計算 する必要があるので、その値を計算する
alphaを負の無限大で初期化 する。負の無限大を利用した最大値の計算の方法 について忘れた方は以前の記事を復習すること -
10 行目:
ab_search(mb)によって計算された子ノードの評価値をscoreに代入する -
11 行目:max ノードの場合は
max関数を利用してscoreとalphaの最大値をalphaに代入することで、alphaにそれまでに計算した子ノードの評価値の最大値を代入する -
12 行目:合法手に対する繰り返し処理の終了後では、
alphaに子ノードの評価値の最大値が計算されて代入されるので、alphaを返り値として返すように修正する - 13 ~ 20 行目:上記と同様の方法で × の手番の min ノード の場合の子ノードの最小値を表す β 値 を計算し、返り値として返すように修正する
1 def ai_abs(mb, debug=False):
2 count = 0
3 def ab_search(mborig):
元と同じなので省略
4 legal_moves = mborig.calc_legal_moves()
5 if mborig.turn == Marubatsu.CIRCLE:
6 alpha = float("-inf")
7 for x, y in legal_moves:
8 mb = deepcopy(mborig)
9 mb.move(x, y)
10 score = ab_search(mb)
11 alpha = max(alpha, score)
12 return alpha
13 else:
14 beta = float("inf")
15 for x, y in legal_moves:
16 mb = deepcopy(mborig)
17 mb.move(x, y)
18 score = ab_search(mb)
19 beta = min(beta, score)
20 return beta
元と同じなので省略
行番号のないプログラム
def ai_abs(mb, debug=False):
count = 0
def ab_search(mborig):
nonlocal count
count += 1
if mborig.status == Marubatsu.CIRCLE:
return 1
elif mborig.status == Marubatsu.CROSS:
return -1
elif mborig.status == Marubatsu.DRAW:
return 0
legal_moves = mborig.calc_legal_moves()
if mborig.turn == Marubatsu.CIRCLE:
alpha = float("-inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score = ab_search(mb)
alpha = max(alpha, score)
return alpha
else:
beta = float("inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score = ab_search(mb)
beta = min(beta, score)
return beta
score = ab_search(mb)
dprint(debug, "count =", count)
if mb.turn == Marubatsu.CIRCLE:
score *= -1
return score
修正箇所
def ai_abs(mb, debug=False):
count = 0
def ab_search(mborig):
元と同じなので省略
legal_moves = mborig.calc_legal_moves()
- score_list = []
- for x, y in legal_moves:
- mb = deepcopy(mborig)
- mb.move(x, y)
- score_list.append(ab_search(mb))
- if mborig.turn == Marubatsu.CIRCLE:
- return max(score_list)
- else:
- return min(score_list)
+ if mborig.turn == Marubatsu.CIRCLE:
+ alpha = float("-inf")
+ for x, y in legal_moves:
+ mb = deepcopy(mborig)
+ mb.move(x, y)
+ score = ab_search(mb)
+ alpha = max(alpha, score)
+ return alpha
+ else:
+ beta = float("inf")
+ for x, y in legal_moves:
+ mb = deepcopy(mborig)
+ mb.move(x, y)
+ score = ab_search(mb)
+ beta = min(beta, score)
+ return beta
元と同じなので省略
上記から、max ノードでは全ての子ノードの評価値を計算した後の α 値に子ノードの評価値の最大値が計算されるので、α 値 は max ノードの評価値を計算 していることがわかります。同様に、β 値 は min ノードの評価値を計算 しています。
上記のプログラムの 7 ~ 10 行目と 15 ~ 18 行目は全く同じプログラムなので、その部分をまとめることもできますが、ただでさえわかりづらい αβ 法のプログラムがさらにわかりづらくなるのでまとめないことにします。なお、まとめる方法については、今回の記事の最後で紹介しましたのでそちらを参照して下さい。
上記の修正は、α 値と β 値を計算する処理を行っているだけで、枝狩りの処理はまだ実装していない ので、ai_abs は ai_mmdfs と同じ処理 を行います。実際に下記のプログラムを実行すると、実行結果のように ai_mmdfs と同じ結果が表示される ことが確認できます。
なお、count の表示は前回の記事 で実装した、debug=True を実引数に記述した際に表示される、探索を行ったノードの数(ノードの評価値を計算するために ab_search を呼び出した回数)を表します。
mb = Marubatsu()
print(ai_abs(mb, debug=True))
実行結果
count = 549946
0
α 狩りと β 狩りの実装
α 狩り を行うためには、min ノードの子ノードの評価値を計算する際 に、その 親ノードで計算した α 値の情報が必要 になります。そのため、仮引数 mmorig に代入された min ノードの評価値を計算 する処理で α 狩りを行う ためには ab_search に α 値を代入する仮引数を追加 する必要があります。これは β 狩りを行う際も同様 なので、ab_search に α 値と β 値を代入するための 仮引数 alpha、beta を追加 することにします。下記は 追加した仮引数を利用 して α 狩りと β 狩りを行う ように ai_abs を修正したプログラムです。
-
3 行目:
ab_searchに仮引数alphaとbetaを追加する -
10 行目:〇 の手番の max ノードの 子ノードは min ノード なので、その min ノード の評価値を計算する際に α 狩りを行うためには α 値が必要 になる。そのため、子ノードの評価値を計算 する処理を行う
ab_searchを呼び出す際に α 値に対応する実引数alphaを記述 する。また、β 値は必要がない ので対応する実引数にNoneを記述する2 -
11、12 行目:max ノードの子ノードの評価値 が β 値以上の場合 は、残りの子ノードの評価値を計算する必要がないので、計算した評価値 をこのノードの評価値として return 文で返す 処理を行う。return 文が実行されると
ab_searchの処理が終了し、残りの子ノード の評価値を計算する 処理が行われなくなる ため、β 狩りが行われた ことになる - 20 ~ 22 行目:min ノードの場合の子ノードの評価値の計算や、α 狩りの処理を、上記と同様の方法で行う
-
26 ~ 28 行目:
ai_absが評価値を計算するノードは、兄弟ノードの評価値が計算されることはない。そのため、そのノードが max ノード の場合は β 値 として 正の無限大を設定 する。α 値 は子ノードの評価値を計算する際に 必要がないのでNoneを設定 する - 29 ~ 31 行目:min ノードの場合に上記と同様の処理を行う
-
32 行目:
ai_absの実引数にalphaとbetaを記述するように修正する
1 def ai_abs(mb, debug=False):
2 count = 0
3 def ab_search(mborig, alpha, beta):
元と同じなので省略
4 legal_moves = mborig.calc_legal_moves()
5 if mborig.turn == Marubatsu.CIRCLE:
6 alpha = float("-inf")
7 for x, y in legal_moves:
8 mb = deepcopy(mborig)
9 mb.move(x, y)
10 score = ab_search(mb, alpha, None)
11 if score >= beta:
12 return score
13 alpha = max(alpha, score)
14 return alpha
15 else:
16 beta = float("inf")
17 for x, y in legal_moves:
18 mb = deepcopy(mborig)
19 mb.move(x, y)
20 score = ab_search(mb, None, beta)
21 if score <= alpha:
22 return score
23 beta = min(beta, score)
24 return beta
25
26 if mb.turn == Marubatsu.CIRCLE:
27 alpha = None
28 beta = float("inf")
29 else:
30 alpha = float("-inf")
31 beta = None
32 score = ab_search(mb, alpha, beta)
元と同じなので省略
行番号のないプログラム
def ai_abs(mb, debug=False):
count = 0
def ab_search(mborig, alpha, beta):
nonlocal count
count += 1
if mborig.status == Marubatsu.CIRCLE:
return 1
elif mborig.status == Marubatsu.CROSS:
return -1
elif mborig.status == Marubatsu.DRAW:
return 0
legal_moves = mborig.calc_legal_moves()
if mborig.turn == Marubatsu.CIRCLE:
alpha = float("-inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score = ab_search(mb, alpha, None)
if score >= beta:
return score
alpha = max(alpha, score)
return alpha
else:
beta = float("inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score = ab_search(mb, None, beta)
if score <= alpha:
return score
beta = min(beta, score)
return beta
if mb.turn == Marubatsu.CIRCLE:
alpha = None
beta = float("inf")
else:
alpha = float("-inf")
beta = None
score = ab_search(mb, alpha, beta)
dprint(debug, "count =", count)
if mb.turn == Marubatsu.CIRCLE:
score *= -1
return score
修正箇所
def ai_abs(mb, debug=False):
count = 0
- def ab_search(mborig):
+ def ab_search(mborig, alpha, beta):
元と同じなので省略
legal_moves = mborig.calc_legal_moves()
if mborig.turn == Marubatsu.CIRCLE:
alpha = float("-inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
- score = ab_search(mb, alpha, None)
+ score = ab_search(mb, alpha, None)
+ if score >= beta:
+ return score
+ alpha = max(alpha, score)
return alpha
else:
beta = float("inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
- score = ab_search(mb)
+ score = ab_search(mb, None, beta)
+ if score <= alpha:
+ return score
beta = min(beta, score)
return beta
元と同じなので省略
+ if mb.turn == Marubatsu.CIRCLE:
+ alpha = None
+ beta = float("inf")
+ else:
+ alpha = float("-inf")
+ beta = None
- score = ab_search(mb)
+ score = ab_search(mb, alpha, beta)
元と同じなので省略
上記の修正後に下記のプログラムを実行すると、実行結果からゲーム開始時の局面の評価値を計算するために ab_search で評価値の計算を行ったノードの数 が約 55 万から 約 3 万に大幅に減った ことが確認でき、αβ 法による枝狩りが実際に行われたことが確認できます。また、枝狩りが行われた結果、下記のプログラムの 処理時間 が約 30 秒から 約 1 秒に大幅に短縮 されるため αβ 法が大きな効果を持つ ことが確認できました。
print(ai_abs(mb, debug=True))
実行結果
count = 29257
0
mborig が max ノード の場合は、仮引数 alpha に None が、beta に β 値 が代入された状態で ab_search が呼び出されますが、そのうちの alpha は ab_search の中の下記のプログラムで負の無限大が代入され、その後の繰り返し処理で 評価値の最大値が代入 されるので、alpha に最初に代入された None が使われることはありません。一方、beta は仮引数に代入された値が そのまま利用 され、ab_search の処理の中で その値が変更されることはありません。
if mborig.turn == Marubatsu.CIRCLE:
alpha = float("-inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score = ab_search(mb, alpha, None)
if score >= beta:
return score
alpha = max(alpha, score)
mborig が min ノードの場合は、上記の alpha と beta の説明が逆になります。
祖先ノードを考慮した α 狩りとβ 狩りの実装
次に、下記の 祖先ノードを考慮 した α 狩りと β 狩りの実装することにします。
-
min ノード では、下記の手順で α 狩り を行う
- 祖先ノード の中の max ノード をすべて探す
- 探した max ノードの中で、評価値が計算済 の 子ノードの評価値の最大値を α とする
- 子ノードの中で α 以下 の評価値が 計算された時点 で 残りの子ノードの評価値の計算を省略 する
-
max ノード では、下記の手順で β 狩り を行う
- 祖先ノード の中の min ノード をすべて探す
- 探した min ノードの中で、評価値が計算済 の 子ノードの評価値の最小値を β とする
- 子ノードの中で β 以上 の評価値が 計算された時点 で 残りの子ノードの評価値の計算を省略 する
先程は、max ノード子ノードの計算 を行う際に、下記のプログラムのように α 値のみ を子ノードの処理を行う ab_search に伝えました が、祖先ノードの評価値を考慮 するためには、ab_search に α 値と β 値の両方を伝える必要 があります。どのように伝えればよいかについて少し考えてみて下さい。
if mborig.turn == Marubatsu.CIRCLE:
score = ab_search(mb, alpha, None)
先程のプログラムでは、max ノードの α 値を計算 する際に、兄弟ノードの評価値のみを考慮 して計算を行っていたため、ab_search の中で α 値を計算する変数 を 負の無限大で初期化 してから計算を行いました。
max ノードで計算する α 値 は子ノードの評価値が計算された際に、それまでの α 値と子ノードの 最大値で更新されます。そのため、祖先ノードの max ノードの α 値 を 子ノードに伝え、max ノードで α 値 を計算する際に負の無限大ではなく、伝えられた α 値から 計算することで、α 値の値は 祖先ノードの max ノードの α 値の最大値 になります。
例えば、下図の 赤枠の max ノードの α 値を計算 する際には、負の無限大からではなく、祖先ノードの青枠 max ノードの α 値 である 1 を α 値の初期値 として計算します。

上図のような処理を行うためには、min ノード では、親ノードから受け取った alpha の値 を、子ノードの評価値を計算する処理に受け渡す 必要があります。現状では α 値は max ノードから子ノードに実引数で伝わりますが、min ノード では下記のプログラムのように alpha の実引数に None が代入 されて ab_search が呼び出されるので 伝わりません。
score = ab_search(mb, None, beta)
そこで、min ノード で ab_search を呼び出す際に、下記のプログラムのように親ノードから受け取った alpha に代入された α 値 を そのまま 子ノードの評価値を計算する処理に 受け渡す ように修正します。
score = ab_search(mb, alpha, beta)
また、max ノードでも同様 に β 値をそのまま 子ノードの評価値を計算する処理に 受け渡す ように修正します。
α 値と β 値 の値が、親ノードから仮引数 alpha と beta で 受け渡されるようになった ので、それらを正または負の無限大で 初期化する処理を削除する 必要があります。
ai_abs で mb の評価値を計算する局面を計算するために 最初に ab_search を呼び出す際 には、α 値 と β 値の両方に適切な値を受け渡す 必要があります。α 値は祖先ノードの α 値の最大値、β 値は祖先ノードの β 値の最小値を表し、その場合に 祖先ノードは存在しない ため、それぞれに負の無限大と正の無限大を設定します。
下記は、そのように ab_search を修正したプログラムです。
- 6、14 行目の後にあった、
alphaまたはbetaを正の無限大または負の無限大で初期化する処理を削除する -
9、18 行目:max ノードでも、min ノードでも子ノードの評価値を計算する際に α 値と β 値の両方を実引数に記述 して
ab_searchを呼び出すように修正する - 24 行目の前の
alphaとbetaを計算する処理を削除する -
24 行目:
ai_absでmbのノードの評価値を計算するためにab_searchを呼び出す際に、α 値と β 値にそれぞれの負の無限大と正の無限大を記述して呼び出すように修正する
1 def ai_abs(mb, debug=False):
2 count = 0
3 def ab_search(mborig, alpha, beta):
元と同じなので省略
4 legal_moves = mborig.calc_legal_moves()
5 if mborig.turn == Marubatsu.CIRCLE:
6 for x, y in legal_moves:
7 mb = deepcopy(mborig)
8 mb.move(x, y)
9 score = ab_search(mb, alpha, beta)
10 if score >= beta:
11 return score
12 alpha = max(alpha, score)
13 return alpha
14 else:
15 for x, y in legal_moves:
16 mb = deepcopy(mborig)
17 mb.move(x, y)
18 score = ab_search(mb, alpha, beta)
19 if score <= alpha:
20 return score
21 beta = min(beta, score)
22 return beta
23
24 score = ab_search(mb, float("-inf") , float("inf"))
元と同じなので省略
行番号のないプログラム
def ai_abs(mb, debug=False):
count = 0
def ab_search(mborig, alpha, beta):
nonlocal count
count += 1
if mborig.status == Marubatsu.CIRCLE:
return 1
elif mborig.status == Marubatsu.CROSS:
return -1
elif mborig.status == Marubatsu.DRAW:
return 0
legal_moves = mborig.calc_legal_moves()
if mborig.turn == Marubatsu.CIRCLE:
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score = ab_search(mb, alpha, beta)
if score >= beta:
return score
alpha = max(alpha, score)
return alpha
else:
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score = ab_search(mb, alpha, beta)
if score <= alpha:
return score
beta = min(beta, score)
return beta
score = ab_search(mb, float("-inf") , float("inf"))
dprint(debug, "count =", count)
if mb.turn == Marubatsu.CIRCLE:
score *= -1
return score
修正箇所
def ai_abs(mb, debug=False):
count = 0
def ab_search(mborig, alpha, beta):
元と同じなので省略
legal_moves = mborig.calc_legal_moves()
if mborig.turn == Marubatsu.CIRCLE:
- alpha = float("-inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
- score = ab_search(mb, alpha, None)
+ score = ab_search(mb, alpha, beta)
if score >= beta:
return score
alpha = max(alpha, score)
return alpha
else:
- beta = float("inf")
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
- score = ab_search(mb, None, beta)
+ score = ab_search(mb, alpha, beta)
if score <= alpha:
return score
beta = min(beta, score)
return beta
- if mb.turn == Marubatsu.CIRCLE:
- alpha = None
- beta = float("inf")
- else:
- alpha = float("-inf")
- beta = None
- score = ab_search(mb, alpha, beta)
+ score = ab_search(mb, float("-inf") , float("inf"))
元と同じなので省略
上記の修正後に下記のプログラムを実行すると、実行結果からゲーム開始時の局面の評価値を計算するために探索したノードの数が約 3 万から 約 2 万に減った ことが確認できます。
print(ai_abs(mb, debug=True))
実行結果
count = 18297
0
AI の関数としての ai_abs の定義
先程のプログラムでは 24 行目で 最初に ab_search を呼び出す際 に α 値と β 値の実引数を記述 しましたが、その代わりに ab_search の 仮引数 alpha と beta をそれぞれ 負の無限大と正の無限大をデフォルト値とする仮引数 として定義できます。
ai_abs は、仮引数として局面を表すデータを代入する mb と、デバッグ表示を行うかどうかを表す debug を持ち、局面の評価値を返す関数として定義したので、@ai_by_score のデコレーター式を記述 することで AI の関数として定義 することができます。
下記は、そのように ai_abs を修正したプログラムです。
-
3 行目:
@ai_by_scoreのデコレータ式を記述する -
6 行目:
alphaとbetaをデフォルト引数に修正する -
7 行目:最初に
ab_searchを呼び出す際に、α 値とβ 値の実引数を省略する
1 from ai import ai_by_score
2
3 @ai_by_score
4 def ai_abs(mb, debug=False):
5 count = 0
6 def ab_search(mborig, alpha=float("-inf"), beta=float("inf")):
元と同じなので省略
7 score = ab_search(mb)
元と同じなので省略
行番号のないプログラム
from ai import ai_by_score
@ai_by_score
def ai_abs(mb, debug=False):
count = 0
def ab_search(mborig, alpha=float("-inf"), beta=float("inf")):
nonlocal count
count += 1
if mborig.status == Marubatsu.CIRCLE:
return 1
elif mborig.status == Marubatsu.CROSS:
return -1
elif mborig.status == Marubatsu.DRAW:
return 0
legal_moves = mborig.calc_legal_moves()
if mborig.turn == Marubatsu.CIRCLE:
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score = ab_search(mb, alpha, beta)
if score >= beta:
return score
alpha = max(alpha, score)
return alpha
else:
for x, y in legal_moves:
mb = deepcopy(mborig)
mb.move(x, y)
score = ab_search(mb, alpha, beta)
if score <= alpha:
return score
beta = min(beta, score)
return beta
score = ab_search(mb)
dprint(debug, "count =", count)
if mb.turn == Marubatsu.CIRCLE:
score *= -1
return score
修正箇所
+from ai import ai_by_score
+@ai_by_score
def ai_abs(mb, debug=False):
count = 0
- def ab_search(mborig, alpha, beta):
+ def ab_search(mborig, alpha=float("-inf"), beta=float("inf")):
元と同じなので省略
- score = ab_search(mb, float("-inf") , float("inf"))
+ score = ab_search(mb)
元と同じなので省略
上記の修正後に、下記のプログラムで ai_abs が 強解決の AI であるか どうかを確認すると、実行結果のように 強解決の AI であることが確認できました。
from util import Check_solved
print(Check_solved.is_strongly_solved(ai_abs))
実行結果
100%|██████████| 431/431 [00:03<00:00, 114.97it/s]
431/431 100.00%
(True, [])
αβ 法による枝狩りの効率
αβ 法 によって どれだけの枝狩りを行うことができるか については、ゲーム木の内容によって大きく異なります。最も多く枝帰りを行うことができる のは、それぞれのノードの 子ノードが評価値の高い順(min ノードの場合は低い順)に並んでいる場合 で、その場合は基本的に各ノードの 最初の子ノードの評価値を計算した時点で枝狩りを行うことができる ため、最も枝狩りを多く行うことができます。具体的な計算方法は長くなるので示しませんが、最高で元のノードの数が n の場合は探索するノードの数を $\sqrt{n}$ まで減らすことができます。
〇×ゲームの ゲーム開始時の局面 の場合は、ミニマックス法で 549946、αβ 法で 18297 個のノードの評価値を計算する必要があります。$\sqrt{549946} = 約 740$ なので、理想的ではありませんが、それでも 約 1/30 に減っている ので αβ 法は確かに大きな効果 があります。
ネガマックス法とネガアルファ法
ミニマックス法と、αβ 法では max ノードと min ノードで行う処理で 同じような処理を 2 回記述 する必要があります。max ノードと min ノードは交互に現れる ので、評価値を計算する 関数の返り値の符号などを反転させる ことで、常に 子ノードの評価値の 最大値を計算するように、max ノードと min ノードの処理を 1 つにまとめる という手法があります。符号を反転(negative)する ことから、そのようなアルゴリズムの事をそれぞれ ネガマックス法 と ネガアルファ法 と呼びます。
ネガマックス法とネガアルファ法は確かに処理を短く記述できますが、ただでさえわかりづらいミニマックス法や αβ 法の プログラムの意味がさらにわかりづらくなる3という欠点があるので、本記事では採用しません。具体的なプログラムの記述方法について興味がある方は、下記の Wikipedia のリンク先を参照して下さい。
今回の記事のまとめ
今回の記事では αβ 法の仕組みの説明と、その実装を行いました。
本記事で入力したプログラム
| リンク | 説明 |
|---|---|
| marubatsu.ipynb | 本記事で入力して実行した JupyterLab のファイル |
| ai.py | 本記事で更新した ai_new.py |
次回の記事