Pythonで〇×ゲームのAIを一から作成する　その177　正規分布に従う離散型確率分布の計算

Last updated at 2025-06-29Posted at 2025-06-22

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

リンク	説明
marubatsu.py	Marubatsu、Marubatsu_GUI クラスの定義
ai.py	AI に関する関数
test.py	テストに関する関数
util.py	ユーティリティ関数の定義
tree.py	ゲーム木に関する Node、Mbtree クラスなどの定義
gui.py	GUI に関する処理を行う基底クラスとなる GUI クラスの定義

AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。

用語と記号

今回の記事では前回の記事に引き続き下記の表の用語と記号を用いることにします。

用語と記号	意味
正確なミニマックス値	深さの制限がないゲーム木の探索によって計算される、局面の正確なミニマックス値のこと
近似値	静的評価関数が計算する正確なミニマックス値とは異なる不正確な値が計算される場合がある評価値のこと
近似値のミニマックス値	深さ制限探索によって計算される、静的評価関数が計算する近似値に対するミニマックス値のこと
$\boldsymbol{d}$	局面の形勢判断の難しさを表す数値
$\boldsymbol{N(d)}$	局面の形勢判断の難しさが $d$ の局面の集合
$\boldsymbol{M(d)}$	$N(d)$ の局面に対して静的評価関数が計算する近似値の平均値
$\boldsymbol{S(d)}$	$N(d)$ の局面に対して静的評価関数が計算する近似値の標準偏差（standard variation）
$\boldsymbol{N_{mean}(s)}$	$M(d) = s$ となる局面の集合。静的評価関数のばらつきをなくした場合にその局面に対して計算される近似値が $s$ となる局面の集合

平均値と期待値の用語について

前回の記事では脚注で 確率分布の平均値 のことを、データの集合から複数のデータを取り出した場合に 想定される平均値 であることから、期待値 と呼ぶと説明しました。一方で、今回の記事で紹介する 確率分布の一種 である 正規分布 の下記の Wikipedia などを見ると、期待値ではなく 平均という用語が使われている ようです。

これまでは、本記事では平均値と期待値の用語を区別して使い分けてきましたが、上記のようなことがあることから、本記事では以後は区別せずに平均と表記することにします。

「平均」と「平均値」は同じ意味の用語だと思います。これまでは平均値と記述してきましたが、上記の Wikipedia に倣って以後は平均と表記することにします。

正規分布で期待値ではなく、平均という用語が一般的に使われている理由については、用語が用いられる文脈の違いではないかと思います。ただし、正直にいうと筆者もそのことを正確に説明できる自信はありませんので説明は省略します。興味がある方は調べてみて下さい

`calc_pdist` の改良

前回の記事では、深さの上限が 1 の場合の深さ制限探索で計算される 近似値のミニマックス値 の 確率分布の計算 を行う calc_pdist を定義しましたが、calc_pdist には以下のような欠点があります。

2 つの子ノード を持つ max ノード の場合しか計算できない

そこで、下記のように calc_pdist 修正することで、任意の数の子ノード と、ルートノードが min ノードの場合にも対応できる ように修正することにします。

複数の子ノード が計算する近似値の確率分布（probability distribution）の一覧を表す list を代入する仮引数 pdistlist を追加し、仮引数 pdistA と pdistB を削除する
ルートノードが max ノードであるかどうか を表す仮引数 maxnode を追加する

下記はそのように calc_pdist を修正したプログラムです。

4 行目：仮引数を pdistlist と、デフォルト値を True とする maxnode に修正する
6 行目：pdistlist のそれぞれの要素を、dict の items メソッドの返り値に置き換える。この処理が必要な理由について忘れた方は前回の記事を復習すること
7 行目：前回の記事で説明した product は、実引数に記述されたデータの直積を計算するので、以前の記事で説明した反復可能オブジェクトの展開を利用して pdistlist の各要素の直積を計算する
8 行目：直積の集合の各要素に対する繰り返し処理を行う
9 行目：直積の要素が代入された data には、それぞれの子ノードの (近似値, 確率) という tuple を要素に持つ list が代入されている。先頭の list の要素から最初の子ノードで計算された近似値とその確率を取り出して score と prob に代入する
10 行目：data の 2 番目以降の要素に対する繰り返し処理を行う
11 ~ 14 行目：ノードの種類に応じた score の値の更新を行う
15 行目：data に記録された子ノードの近似値の組み合わせが計算される確率は、それぞれの近似値が計算される確率を乗算した値となるので、その計算を行う
16、17 行目：元のプログラムと同じ

 1  from collections import defaultdict
 2  from itertools import product
 3  
 4  def calc_pdist(pdistlist, maxnode=True):
 5      pdist = defaultdict(int)
 6      pdistlist = [pd.items() for pd in pdistlist]
 7      productdata = product(*pdistlist)
 8      for data in productdata:
 9          score, prob = data[0]
10          for s, p in data[1:]:
11              if maxnode:
12                  score = max(score, s)
13              else:
14                  score = min(score, s)
15              prob *= p
16          pdist[score] += prob
17      return pdist

行番号のないプログラム

from collections import defaultdict
from itertools import product

def calc_pdist(pdistlist, maxnode=True):
    pdist = defaultdict(int)
    pdistlist = [pd.items() for pd in pdistlist]
    productdata = product(*pdistlist)
    for data in productdata:
        score, prob = data[0]
        for s, p in data[1:]:
            if maxnode:
                score = max(score, s)
            else:
                score = min(score, s)
            prob *= p
        pdist[score] += prob
    return pdist

修正箇所

from collections import defaultdict
from itertools import product

-def calc_pdist(pdistA, pdistB):
+def calc_pdist(pdistlist, maxnode=True):
    pdist = defaultdict(int)
+   pdistlist = [pd.items() for pd in pdistlist]
-   productdata = product(pdistA.items(), pdistB.items())
+   productdata = product(*pdistlist)
-   for ((scoreA, probA), (scoreB, probB)) in productdata:
-       score = max(scoreA, scoreB)
-       prob = probA * probB
-       result[score] += prob
+   for data in productdata:
+       score, prob = data[0]
+       for s, p in data[1:]:
+           if maxnode:
+               score = max(score, s)
+           else:
+               score = min(score, s)
+           prob *= p
+       pdist[score] += prob
    return pdist

上記の修正後に、前回の記事と同じ 下記の設定で深さの上限を 1 とした深さ制限探索での ノード $\boldsymbol{N}$ の近似値のミニマックス値の 確率分布の計算 を行い、結果が同じになる ことで calc_pdist が 正しく動作することを確認 することにします。

静的評価関数が任意の $d$ に対して下記の表の確率分布で近似値を計算する
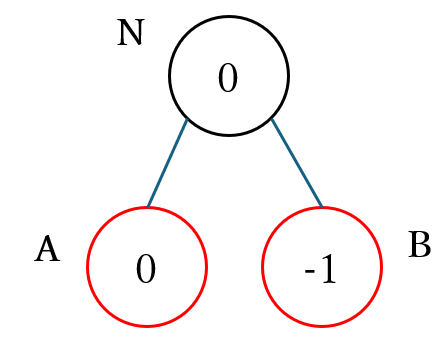
max ノードであるノード $N$ が下図のように子ノード $A$ と $B$ を持つ。なおノードの黒枠が max ノードを、赤枠が min ノードを表す
ノード $A$ と $N$ は $N_{mean}(0)$、ノード $B$ は $N_{mean}(-1)$ の集合に属する。図のノードの中の数値がそのノードが属する $N_{mean}(s)$ の集合の $s$ を表す

近似値の平均 $\boldsymbol{M(d)}$ との差	-2	-1	0	1	2
局面の割合	5%	20%	50%	20%	5%

下記はその計算を行うプログラムで 前回の記事と同じ計算結果 になることが確認できます。

from pprint import pprint
from tree import calc_stval

pdistA = {
    -2: 0.05,
    -1: 0.2,
     0: 0.5,
     1: 0.2,
     2: 0.05
}
pdistB = {
    -3: 0.05,
    -2: 0.2,
    -1: 0.5,
     0: 0.2,
     1: 0.05
}
pdistNmax = calc_pdist([pdistA, pdistB], maxnode=True)
pprint(pdistNmax)
print(calc_stval(pdistNmax))

実行結果

defaultdict(<class 'int'>,
            {-2: 0.012500000000000002,
             -1: 0.17500000000000002,
             0: 0.525,
             1: 0.23750000000000004,
             2: 0.05000000000000001})
(0.13750000000000007, 0.6435937500000002, 0.8022429494860022)

次に、下図のようにノード $N$ を min ノードとした場合 の計算を行うことにします。ノード $N$ は min ノード なので、下図のように $\boldsymbol{N_{mean}(-1)}$ の集合に属する ことになります。

下記はその計算を行うプログラムです。

pdistNmin = calc_pdist([pdistA, pdistB], maxnode=False)
pprint(pdistNmin)
print(calc_stval(pdistNmin))

実行結果

defaultdict(<class 'int'>,
            {-3: 0.05000000000000001,
             -2: 0.23750000000000004,
             -1: 0.525,
             0: 0.17500000000000002,
             1: 0.012500000000000002})
(-1.1375000000000002, 0.6435937500000001, 0.802242949486002)

min ノードと max ノード で行われる 処理の違い は、子ノードの近似値の 最小値 を計算するか 最大値 を計算するかです。そのため、max ノード の場合に計算される 確率分布 は、min ノード の場合の確率分布と下記の表のように 反転します。なお、表の数値は小数点以下第 5 桁で四捨五入しました。

近似値など	max ノード	min ノード
-3	0.0000	0.05000
-2	0.0125	0.02375
-1	0.1750	0.05250
0	0.5250	0.01750
1	0.2375	0.01250
2	0.0500	0.00000
平均	0.1375	-1.1375
標準偏差	0.8022	0.8022

max ノード の場合は $N$ は $\boldsymbol{N_{mean}(0)}$ の集合に属しており、計算される 確率分布の平均 は 0 から 0.1375 多い値 になります。一方、min ノードの場合は $N$ は $\boldsymbol{N_{mean}(-1)}$ の集合に属しており、計算される 確率分布の平均 は -1 から 0.1375 小さい値 となります。このように、平均も max ノードと min ノードの場合で 反転している ことがわかります。

確率分布の形状 は 反転している ので、ばらつきをあらわす 標準偏差は同じ になります。

次に、calc_pdist が 3 つ以上の子ノード に対応していることを確認することにします。下記は下図のように max ノード $N$ の 3 つ目の子ノード として ノード $\boldsymbol{B}$ と同じ確率分布 で近似値を計算する ノード $\boldsymbol{C}$ が加わった場合の計算を行うプログラムです。実行結果から子ノードが 2 つの場合と比較して平均が 0.138 から 0.229 に 少し上昇し、標準偏差 が 0.802 から 0.755 に 少し減少する ことが確認できます。なお、子ノードの数と平均、標準偏差の具体的な関係については次回の記事で説明します。

pdistN3 = calc_pdist([pdistA, pdistB, pdistB], maxnode=True)
pprint(pdistN3)
print(calc_stval(pdistN3))

実行結果

defaultdict(<class 'int'>,
            {-2: 0.0031250000000000006,
             -1: 0.1375,
             0: 0.5362500000000001,
             1: 0.2731250000000001,
             2: 0.05000000000000002})
(0.22937500000000013, 0.5705121093750002, 0.7553225201031677)

確率分布の視覚化

上記のような 確率分布を表す dict を見ても 実感がわかない と思いますので、実引数に記述した 確率分布のグラフを表示 する draw_pdist を定義することにします。

`draw_pdist` の定義

下記は draw_pdist を定義するプログラムです。以前の記事のノートで matplotlib の hist を利用 して ヒストグラムを描画 する方法を説明しました。hist は 20 代（20 以上 29 以下）の人数を描画するヒストグラムのように、範囲を持つデータの個数 を描画する際には便利ですが、静的評価関数の確率分布のように、確率変数が 範囲を持たない 1 種類のデータ の場合は 棒グラフを描画 する bar を利用したほうが 簡単に描画できる ことに気が付きましたので bar を利用して描画することにします。bar の使い方はは折れ線グラフを描画する plot とほぼ同じ ですが、棒の幅 を表す 仮引数 width を持つ点などが異なります。

bar の詳細については下記のリンク先を参照して下さい。

2 行目：文字化けが起きないようにするために japanize_matplotlib をインポートする
5 行目：pdist のキーが確率変数の値、キーの値が確率変数に対する確率を表すので、pdist.keys() と pdist.values() を bar の実引数に記述して棒グラフを描画する。また、width=1 を記述して棒の幅を 1 にして棒と棒がくっついて描画されるようにした
6, 7 行目：x 軸と y 軸のラベルを描画する

1  import matplotlib.pyplot as plt
2  import japanize_matplotlib
3  
4  def draw_pdist(pdist):
5      plt.bar(pdist.keys(), pdist.values(), width=1)
6      plt.xlabel("近似値")
7      plt.ylabel("確率")

行番号のないプログラム

import matplotlib.pyplot as plt
import japanize_matplotlib

def draw_pdist(pdist):
    plt.bar(pdist.keys(), pdist.values(), width=1)
    plt.xlabel("近似値")
    plt.ylabel("確率")

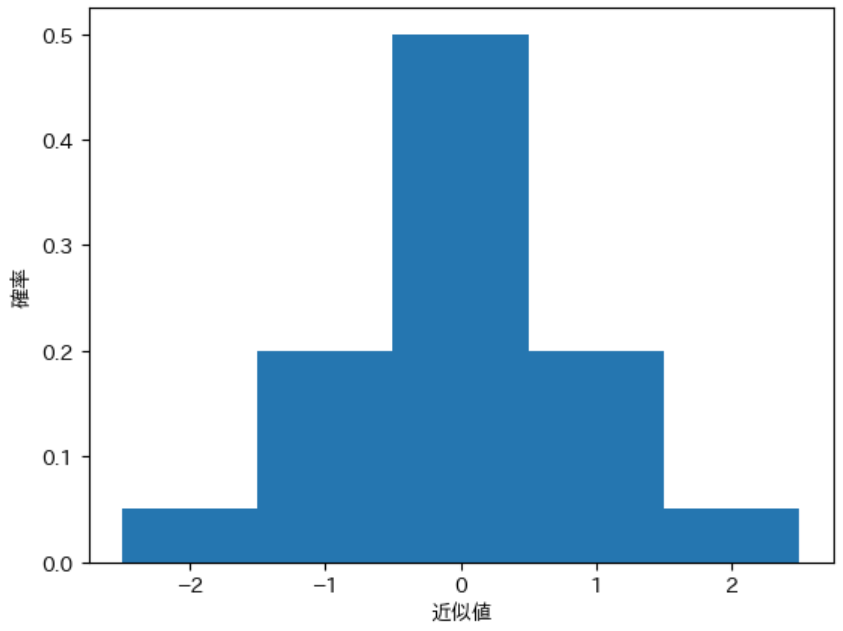
上記の定義後に下記のプログラムで pdistA の確率分布を描画すると、実行結果のようなグラフ描画されます。

draw_pdist(pdistA)

実行結果

下記は pdistA と先程計算した pdistNmax の確率分布を 同時に描画 するプログラムです。

draw_pdist(pdistA)
draw_pdist(pdistNmax)

実行結果

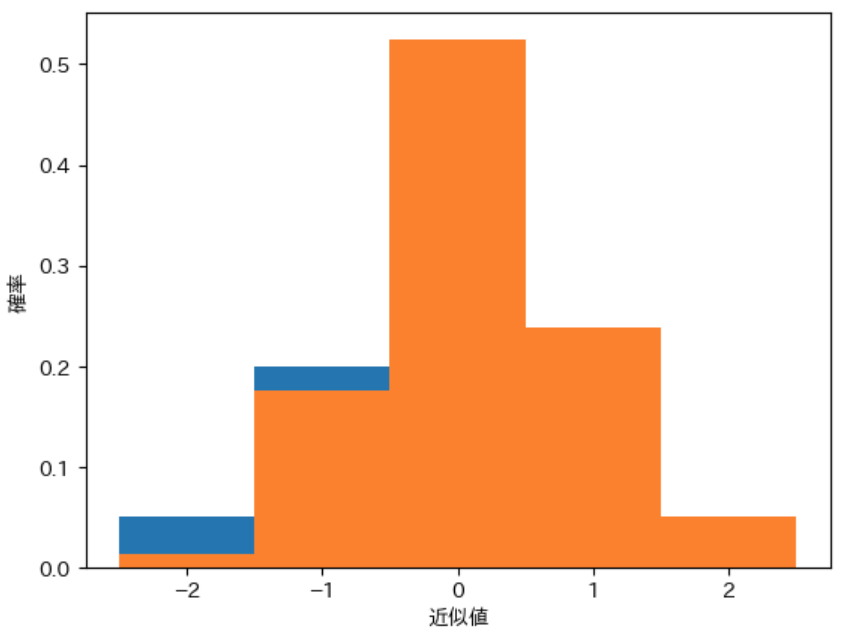
2 つの確率分布のグラフ を draw_pdist で描画すると、実行結果のように 重なった部分 が後から描画したグラフで 上書きされてしまう という問題があることがわかります。

`draw_pdist` の改良

matplotlib の plot や bar などでグラフを描画する際に、透明度 を表す キーワード引数 alpha を記述することで 半透明なグラフ を描画することができます。透明度 は 0 以上 1 以下の実数 で表現し、0 が透明、1 が不透明 を表します。そこで、draw_pdist の 仮引数 にグラフの 透明度を表す alpha を追加 して半透明なグラフを描画できるようにします。

また、複数のグラフを一度に描画 する場合は 凡例を描画 したほうがわかりやすいので、凡例に表示する グラフのラベルを代入する仮引数を追加 することにします。

下記はそのように draw_pdist を改良したプログラムです。

1 行目：グラフのラベルを代入する仮引数 label と、デフォルト値を不透明を表す 1.0 とする仮引数 alpha を追加した
2 行目：キーワード引数 label=label と alpha=alpha を追加した
5 行目：凡例を表示するようにした

1  def draw_pdist(pdist, label, alpha=1.0):
2      plt.bar(pdist.keys(), pdist.values(), width=1, label=label, alpha=alpha)
3      plt.xlabel("近似値")
4      plt.ylabel("確率")
5      plt.legend()

行番号のないプログラム

def draw_pdist(pdist, label, alpha=1.0):
    plt.bar(pdist.keys(), pdist.values(), width=1, label=label, alpha=alpha)
    plt.xlabel("近似値")
    plt.ylabel("確率")
    plt.legend()

修正箇所

-def draw_pdist(pdist):
+def draw_pdist(pdist, label, alpha=1.0):
-   plt.bar(pdist.keys(), pdist.values(), width=1)
+   plt.bar(pdist.keys(), pdist.values(), width=1, label=label, alpha=alpha)
    plt.xlabel("近似値")
    plt.ylabel("確率")
+   plt.legend()

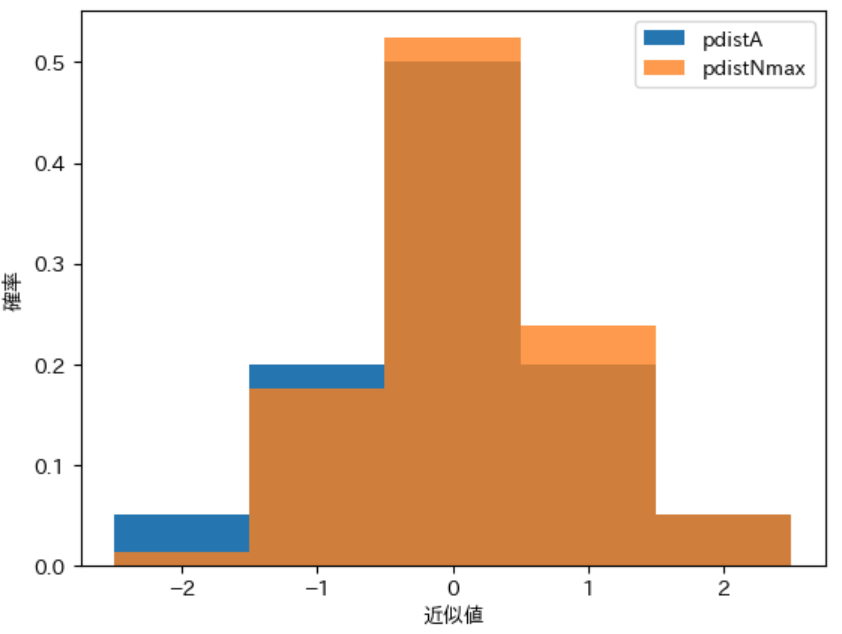
上記の修正後に下記のプログラムを実行すると、実行結果のように pdistNmax のグラフ が透明度が 0.8 の 半透明で描画 されて pdistA のグラフが透けて見える ようになります

draw_pdist(pdistA, label="pdistA")
draw_pdist(pdistNmax, label="pdistNmax", alpha=0.8)

実行結果

正規分布に従う離散型確率分布の作成

これまでに作成した確率分布は確率変数が 5 つしかないシンプルなものでしたが、もっと多い確率変数 を持つ確率分布を 記述するのは大変 です。また、特定の標準偏差 を持つ確率分布を 作成するため には、確率変数とその確率を 何度も調整する必要がある ため大変です。

統計学では 正規分布 という 確率分布 が良く使われており、Python には 指定した平均と標準偏差 を持つ 正規分布を計算するモジュール が存在するので、それを使って静的評価関数が計算する近似値の 確率分布を作成する関数を定義 することにします。

正規分布とは何か

関数を定義する前に、正規分布 について簡単に説明します。正規分布は、下図のような ベル（釣り鐘）のような形状をしたグラフ で表される 確率分布 で、学校で同じ学年の人間の身長や体重を計測した際の分布など、多くの統計データ が 正規分布に似た分布 になることが知られています。そのため、自然科学や社会科学などの様々な場面で、複雑な現象を近似的に表す分布 として よく用いられます。正規分布の性質を持つ分布 の事を、正規分布に従う分布 と表現します。

なお、下記のグラフの描画方法については、後で説明します。

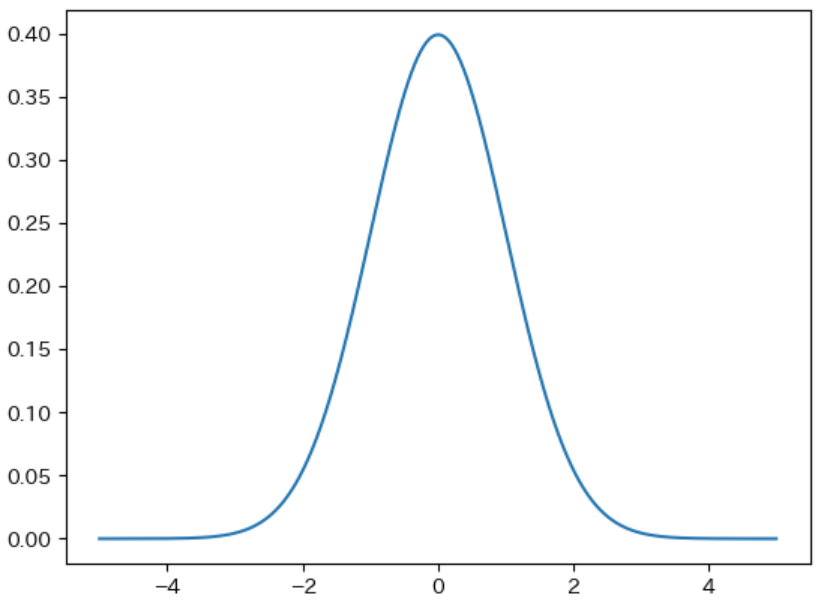
正規分布を表すグラフは、上図のように平均が最も多く、平均から離れるほど小さくなり、平均を中心とした左右対称になります。これは以前の記事で 設定した静的評価関数の性質を満たします。そこで、本記事では局面の形勢判断の難しさが同じ局面に対して 静的評価関数が計算する近似値 が、正規分布に従う ものとして以後の計算を行うことにします。

参考までに正規分布の Wikipedia のリンクを下記に示します。

離散型確率分布と連続型確率分布

確率分布には 離散型確率分布 と 連続型確率分布 があり、正規分布に従う離散型確率分布を作成する際に必要となるのでその性質について説明します。

参考までに確率分布の Wikipedia のリンクを下記に示します。

先程のグラフは 平均が 0、標準偏差が 1 の 正規分布 のグラフです。そのような正規分布のことを 標準正規分布 と呼び、以後の説明では 標準正規分布のグラフ を使って 説明を行う ことにします。

離散型確率分布

本記事では静的評価関数が計算する 近似値を整数とした ので、これまでの確率分布の 確率変数 は -2, -1, 0, 1, 2 のような整数でした。整数のような 飛び飛びの値 を取る数値のことを 離散的 と呼び、離散的な確率変数 を持つ 確率分布 のことを 離散型確率分布 と呼びます。離散型確率分布には以下のような用語と性質があります

確率変数は離散的な値をとるので 離散型確率変数 と呼ぶ
前回の記事で説明した、確率変数 $X$ の要素である $x$ に対応する 確率を計算 する $\boldsymbol{P(x)}$ のことを 確率質量関数 と呼ぶ
確率分布を表す 確率質量関数 をグラフ化すると、ヒストグラムのようなグラフ でグラフ化される。ただし、ヒストグラムの縦軸が個数を表す 0 以上の整数であるのに対して、確率質量関数のグラフの 縦軸は確率を表す ので 0 以上 1 以下の実数 となる

離散型確率分布 の 具体例 としては、サイコロの出目 に対応する 確率分布 などがあります。

連続型確率分布

実数のような 連続した値 を取る数値のことを 連続的 と呼び、連続的な確率変数 を持つの 確率分布 のことを 連続型確率分布 と呼びます。連続型確率分布には以下のような用語と性質があります

確率変数は連続的な値ととるので 連続型確率変数 と呼ぶ
連続型確率分布は確率変数 $X$ の要素である $x$ に対応した $f(x)$ を計算する 確率密度関数 と呼ばれる関数で表される
確率質量関数と異なり、確率密度関数 $\boldsymbol{f(x)}$ そのもの は 確率を表さない
確率変数 $X$ が $\boldsymbol{a ≦ X ≦ b}$ となる確率 は、$\boldsymbol{a ≦ X ≦ b}$ の範囲 の確率密度関数 $\boldsymbol{f(x)}$ と x 軸の間 の面積で表される
確率密度関数 と x 軸との間の面積 は 1 となる。確率密度関数と x 軸との間の面積は 1 となる理由は、$X$ が $-∞ ≦ X ≦ ∞$ となる確率が 1 だからである

例えば、下図の 確率密度関数 を表す 青色のグラフ では、赤色で塗りつぶされた面積 が確率変数 $X$ が $\boldsymbol{a ≦ X ≦ b}$ となる確率 を表します。

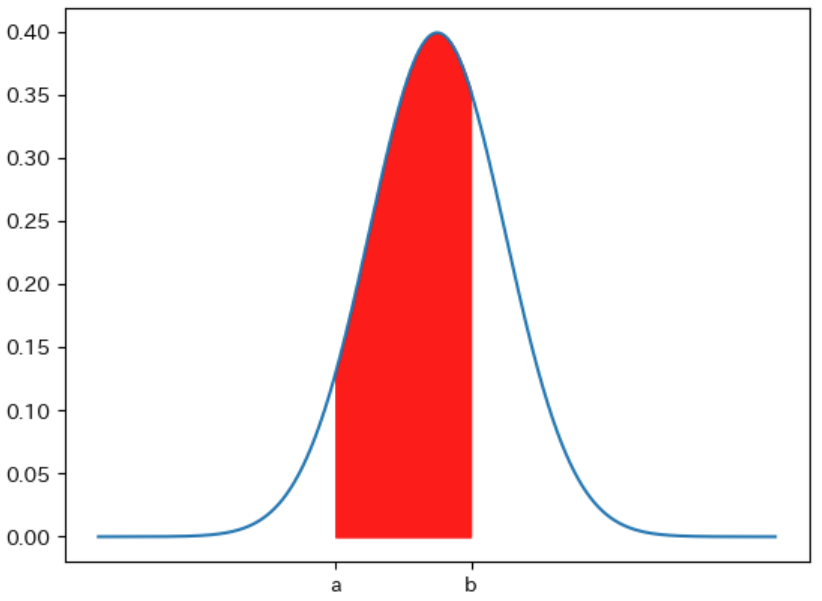
確率密度関数 $f(x)$ が確率を表さない理由は下記の例から明らかです。

例えば下図の平均が 0、標準偏差が 1 の正規分布の確率密度関数では $f(0)$ の値は約 0.4 であることが読み取れます。また 0 の付近の $f(0.1)$ や $f(0.2)$ も約 0.4 であることがわかります。もし、$f(0)$ が確率変数が 0 となる確率を表すとした場合は、確率変数が 0、0.1、0.2 となる 確率の合計 が 0.4 + 0.4 + 0.4 = 1.2 のように 1 を超えてしまう という、おかしなことになります。

別の考え方としては、連続型確率変数 の確率変数の 種類は無限にある ことから、特定の確率変数が起きる確率は 0 となり、確率変数の 範囲を指定する ことではじめてその 確率を求めることができる ようになります。

上記の確率密度関数に関する性質は積分を使った下記の式で表現されます。なお、本記事では積分を使った計算の説明を行う予定は今の所ありませんので、下記の式の意味がわからない人は無視してもかまいません。

確率変数 $X$ が $a ≦ X ≦ b$ となる確率は $\int_{a}^{b}f(x)dx$
$\int_{-∞}^{∞}f(x)dx = 1$

確率密度関数の意味

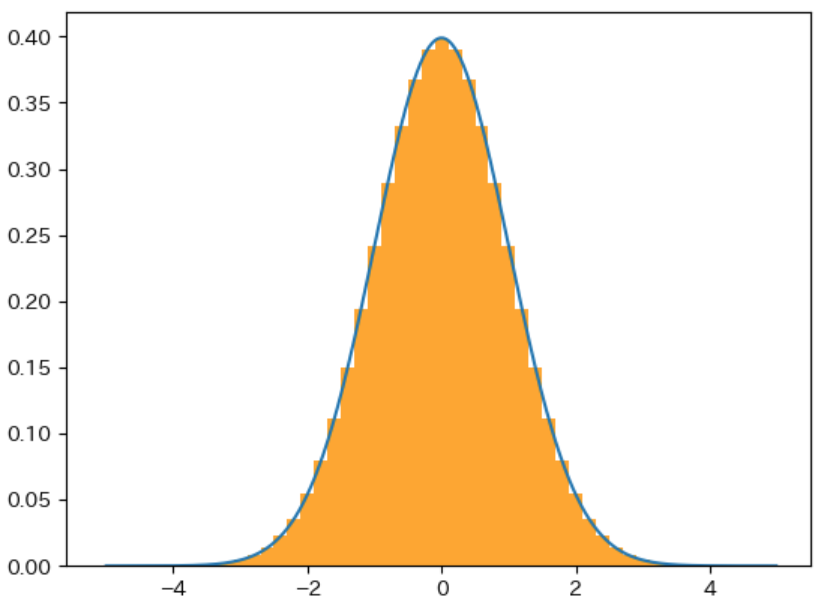
下図の オレンジ色のグラフ は、青色の確率密度関数 の確率分布の 確率変数 を -0.5 ~ 0.5、0.5 ~ 1.5 のように 整数を中心とした幅が 1 の範囲 で区切った場合の それぞれの範囲の確率 を表すグラフです。このように、確率密度関数 の確率変数を 一定の範囲で区切ったグラフ は 確率質量関数のグラフ になります。

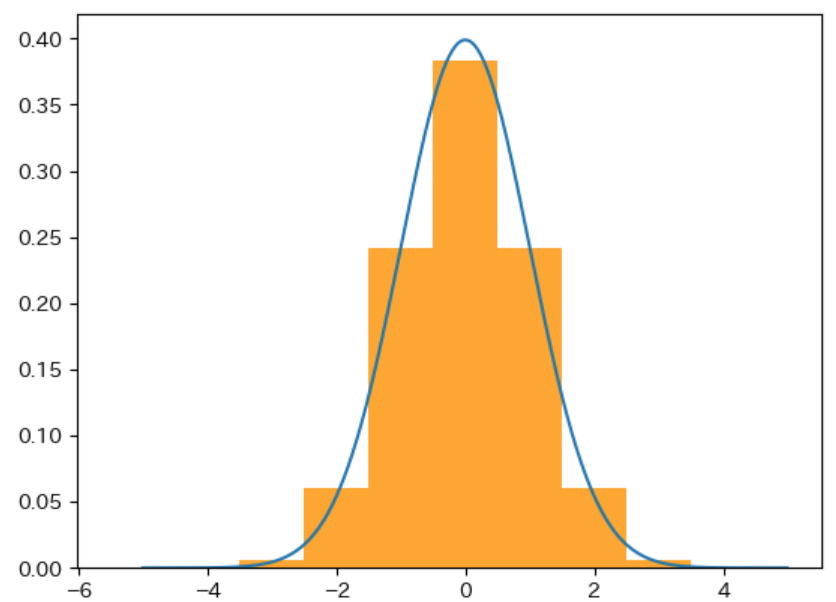
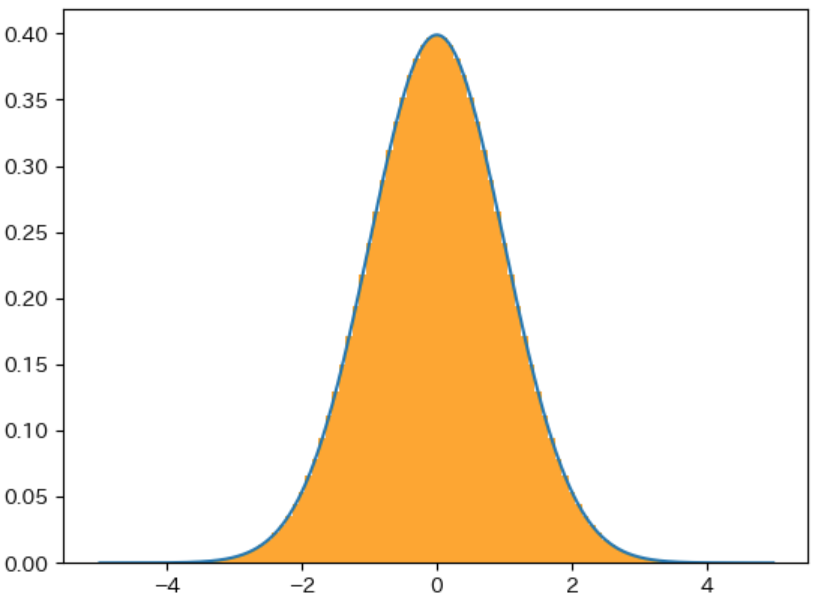
下図は 確率変数 を 0.5、0.2、0.1 ずつ区切った場合 のグラフで、区切る範囲が狭くなるほど 青色の 確率密度関数のグラフと同じ形に近くなる ことがわかります。このことから、確率密度関数 は 確率変数 を 限りなく 0 に近い範囲 で区切った場合の 確率質量関数のグラフ であることがわかります。

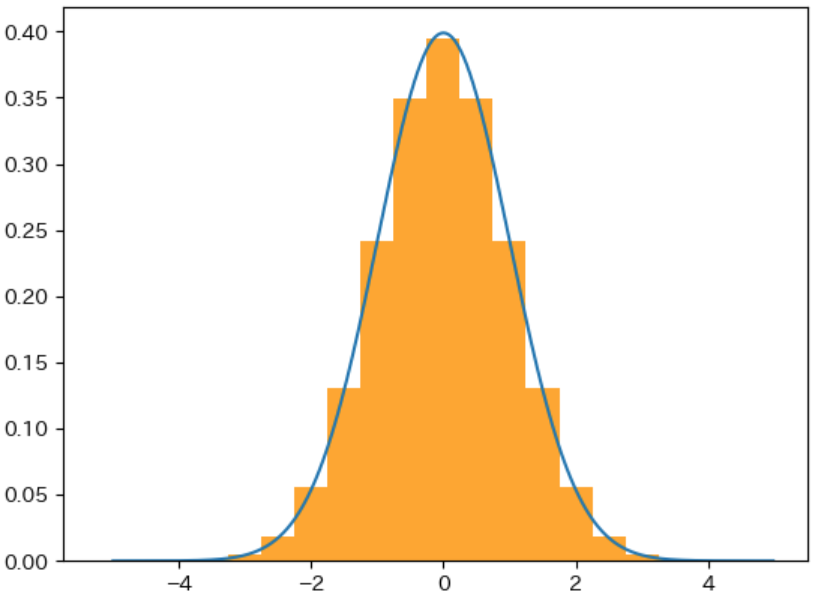
累積分布関数

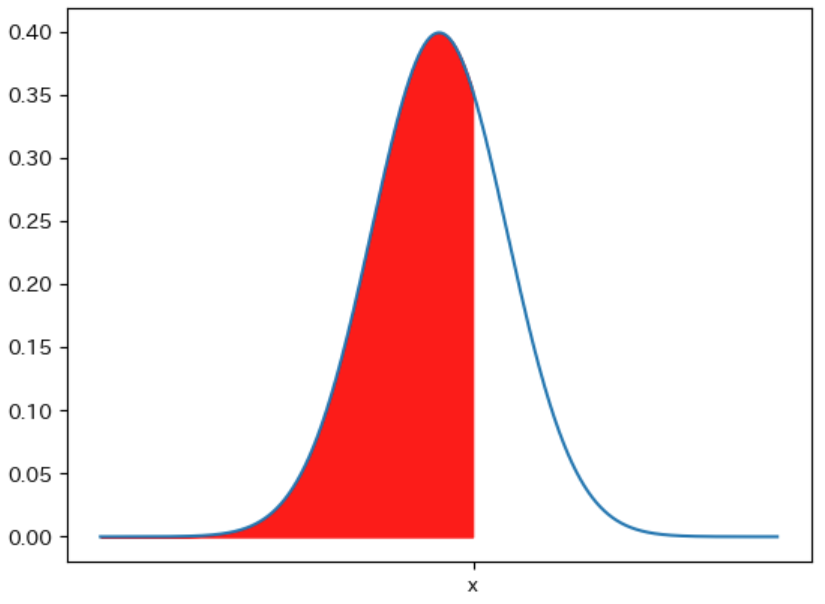
連続型確率分布 の確率変数 $\boldsymbol{X}$ が $\boldsymbol{x}$ 以下となる確率 を表す関数を 累積分布関数 と呼びます。累積分布関数を $\boldsymbol{F(x)}$ と記述した場合に $F(x)$ は下図の 赤色の面積 を表します。

累積分布関数は確率密度関数の積分を使って下記のように定義できます。

$F(a) = \int_{-∞}^{a}f(x)dx$

平均が 0、標準偏差が 1 の正規分布の 累積分布関数のグラフ は下図のようになります。

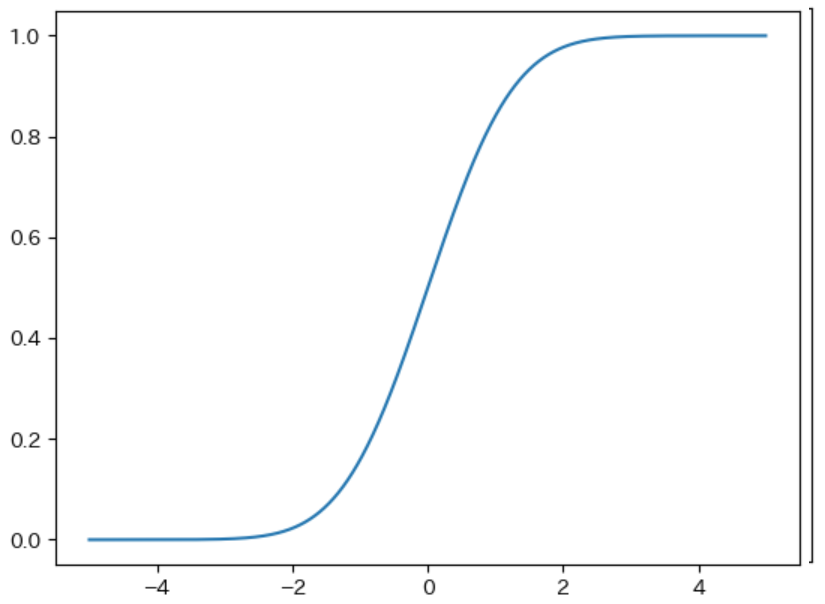
累積分布関数 はその定義から 下記の性質 があります。

$F(-∞) = 0$
$F(∞) = 1$

従って確率変数 $X$ が $\boldsymbol{a ≦ X ≦ b}$ となる確率 は 累積分布関数を利用した下記の式 で計算することができます。

a と b の条件	確率変数の範囲	確率
$\boldsymbol{a = -∞ < b < ∞}$	$X ≦ b$	$F(b)$
$\boldsymbol{-∞ < a < b < ∞}$	$a ≦ X ≦ b$	$F(b) - F(a)$
$\boldsymbol{-∞ < a < b = ∞}$	$a ≦ X$	$1 - F(a)$

正規分布と標準偏差の関係

平均を $μ$、標準偏差を $σ$、確率変数を $X$ とする 正規分布 には下記の性質があります。

確率変数が $\boldsymbol{μ - σ ≦ X ≦ μ + σ}$ の範囲を取る確率は 約 68 % である
確率変数が $\boldsymbol{μ - 2σ ≦ X ≦ μ + 2σ}$ の範囲を取る確率は 約 95 % である
確率変数が $\boldsymbol{μ - 3σ ≦ X ≦ μ + 3σ}$ の範囲を取る確率は 約 99.7 % である

例えば、下記の 平均が 0、標準偏差が 1 の 正規分布 の確率密度関数のグラフでは、$-1 ≦ x ≦ 1$ の範囲の 赤色の面積が約 0.68 となります。

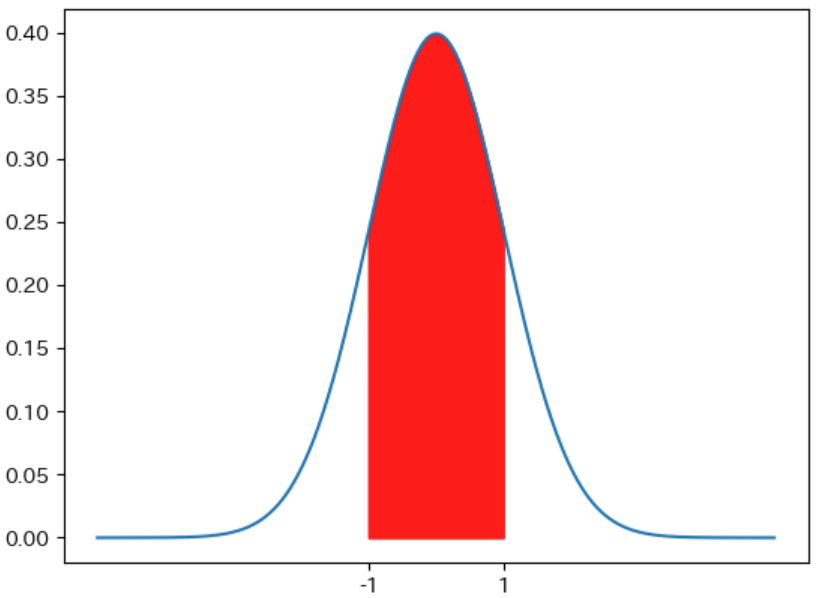
上記を覚えておくことで、データの分布 が 正規分布にほぼ従う ことがわかっている場合は、その 平均と標準偏差を計算 することで、データが 上位何 % であるか を 簡単に知る ことができるようになります。これが 正規分布に従うと仮定 した分析が 良く行われる理由 です。なお、当然ですが 正規分布に従わない場合 は 上記の性質は満たされません。そのため、正規分布であると 安易に仮定して分析を進めるのは危険である ことに注意して下さい。

%%timeit で表示される下記の内容は、JupyterLab のセルに記述したプログラムを 7 × 1000 = 7000 回行った際 の 処理時間の平均が 120 s、標準偏差が 20 s であったことを表します。このことから、セルに記述したプログラムの 処理時間 が 正規分布に従う場合 は、その 68 % の処理 が 120 ± 20 s（100 秒以上 140 秒以下）、95 % の処理 が 120 ± 40 s（80 秒以上 160 秒以下）で行われた ことを意味します。

120 s ± 20 s per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

なお、一般的 にはプログラムの 処理時間 は 正規分布にほぼ従います が、プログラムが行う 処理の種類によって は そうでない場合もある 点に注意が必要です。

テストの結果などで表記される 偏差値 は、テストの結果を 平均が 50、標準偏差が 10 のデータに 変換した時の値 を表します。偏差値が 60 の場合は、テストの結果が正規分布に従っていれば 累積分布関数 から 上位約 15 % の成績 であることを意味します。なお、テストが簡単すぎる場合など、テストの結果が 正規分布に従わない場合 は 上位 15 % ではない ので、偏差値は目安である ことに注意して下さい。

正規分布を扱う NormalDist クラス

Python には正規分布などの 統計学（statistics）に関する関数を集めた statistics モジュール があり、その中で 正規分布（normal distribution）を扱う NormalDist というクラスが定義 されています。正規分布 は 平均と標準偏差に よって 形状が決まる分布 で、NormalDist
の実引数に平均と標準偏差を記述して呼び出すことで、その平均と標準偏差を持つ 正規分布に従う連続型確率分布 を表す NormalDist のインスタンスが作成されます。

下記のプログラムは、平均が 0、標準偏差が 1 の正規分布 を表す NormalDist のクラスのインスタンスを作成し、ndist に代入 しています。

from statistics import NormalDist

ndist = NormalDist(0, 1)

NormalDist クラスの詳細については下記のリンク先を参照して下さい。

正規分布のように、特定のパラメータ（値）の 組み合わせ によって 形状が決まる分布 の事を パラメトリック分布 と呼び、様々なパラメトリック分布が存在します。

例えばサイコロを振った時の出目の確率分布のように、すべての確率変数 に対応する確率が 1/6 で 同じになる確率分布 を 一様分布 と呼びますが、一様分布もパラメトリック分布です。

特定の パラメータ で 形状が決まらない 分布のことを ノンパラメトリック分布 と呼びます。ノンパラメトリック分布には正規分布のような 特定の名前はありません。

確率密度関数を計算する `pdf` メソッド

正規分布 の 確率密度関数（probability density function）は Normaldist の pdf というメソッドで計算できます。そのため、確率密度関数 は下記のプログラムで グラフ化 できます。

1 行目：-5 ~ 5 までの数値を 0.01 刻み で要素として持つ list を X に代入 する。range は整数しか扱えない ため、小数点以下の数値を規則正しく増やす 処理を range で行う 場合は、このように記述する必要がある¹
2 行目：X のそれぞれの要素に対する正規分布の 確率密度関数の値 を pdf で計算 して Y に代入 する
3 行目：X と Y を plot メソッドでグラフ化する

X = [x / 100 for x in range(-500, 500)]
Y = [ndist.pdf(x) for x in X]
plt.plot(X, Y)

実行結果

グラフの塗りつぶしは fill_between というメソッドを利用して描画することができます。また、x 軸のラベルは xticks というメソッドを利用して描画することができます。下記は先ほどのグラフを描画するプログラムです。

X = [x / 100 for x in range(-500, 500)]
Y = [ndist.pdf(x) for x in X]
plt.plot(X, Y)
plt.fill_between(X[350:550], 0, Y[350:550], color="r")
plt.xticks([-1.5, 0.5], labels=["a", "b"])

実行結果

fill_between と xticks の詳細については下記のリンク先を参照して下さい。

確率密度関数を計算する `cdf` メソッド

正規分布の 累積分布関数（cumulative distribution function）は Normaldist の cdf というメソッドで計算できるので、累積分布関数は下記のプログラムでグラフ化できます。

X = [x / 100 for x in range(-500, 500)]
Y = [ndist.cdf(x) for x in X]
plt.plot(X, Y)

実行結果

正規分布に従う離散型確率分布の計算

正規分布に従う、確率変数が整数 の 離散型確率分布 は下記の手順で NomalDist のインスタンスを利用して作成 することができます。

平均と標準偏差を記述 して NormalDist のインスタンス ndist を作成 する
整数の確率変数 $X$ に対する確率を、 $\boldsymbol{X - 0.5 ≦ x ≦ X + 0.5}$ の範囲 の ndist の確率を表す ndist.cdf(X + 0.5) - ndist.cdf(X - 0.5) で計算する

ただし、正規分布 の 確率変数の範囲 は 実数全体 であり、無限に存在する確率変数 に対する確率を 計算することは不可能 なので、本記事では 平均を中心とした特定の範囲 の確率変数の確率を計算することにします。具体的には下記のような関数を定義することにします。

名前：正規分布（normal distribution）に従う離散型（discrete）確率分布を計算するので、calc_discrete_ndist と命名する
処理：指定した平均と標準偏差を持ち、指定した範囲の確率変数に対する確率が計算された離散型確率分布を計算する
入力：仮引数 m に平均、s に標準偏差、area に確率変数の平均からの範囲を代入する
出力：計算した確率分布を返り値として返す

下記は calc_discrete_ndist の定義です。

1 行目：仮引数 m、s、area を持つ関数として定義する
2 行目：平均を m、標準偏差を s とする正規分布を表すデータを計算する
3 行目：作成する離散型確率分布を表す pdist を空の dict で初期化する
4 行目：平均から area の範囲の確率変数の繰り返し処理を行う
5、6 行目：確率変数が m - area の場合は、m - area 以下の範囲の確率を表す ndist.cdf(x + 0.5) を計算する
7、8 行目：確率変数が m + area の場合は、m + area 以上の範囲の確率を表す ndist.cdf(x - 0.5) を計算する
9、10 行目：それ以外の場合は確率変数 x の確率を表す ndist.cdf(x + 0.5) - ndist.cdf(x - 0.5) を計算する
11 行目：計算した確率分布を返り値として返す

 1  def calc_discrete_ndist(m, s, area):
 2      ndist = NormalDist(m, s)
 3      pdist = {}
 4      for x in range(m - area, m + area + 1):
 5          if x == m - area:
 6              pdist[x] = ndist.cdf(x + 0.5)
 7          elif x == m + area:
 8              pdist[x] = 1 - ndist.cdf(x - 0.5)
 9          else:
10              pdist[x] = ndist.cdf(x + 0.5) - ndist.cdf(x - 0.5)
11      return pdist

行番号のないプログラム

def calc_discrete_ndist(m, s, area):
    ndist = NormalDist(m, s)
    pdist = {}
    for x in range(m - area, m + area + 1):
        if x == m - area:
            pdist[x] = ndist.cdf(x + 0.5)
        elif x == m + area:
            pdist[x] = 1 - ndist.cdf(x - 0.5)
        else:
            pdist[x] = ndist.cdf(x + 0.5) - ndist.cdf(x - 0.5)
    return pdist

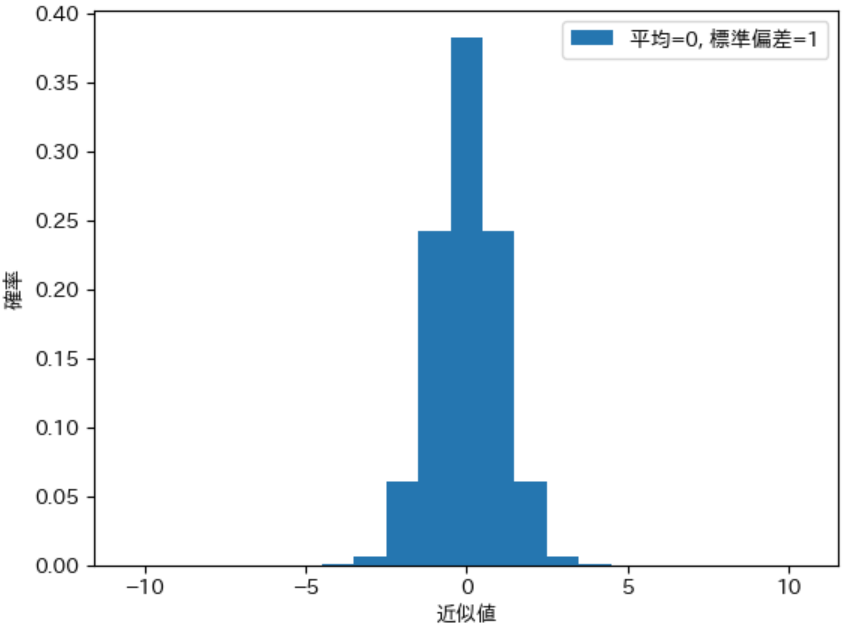
下記のプログラムは 平均が 0、標準偏差が 1、確率変数の範囲を 10 とした場合の 正規分布に従う離散型確率分布 を計算し、その 平均と標準偏差と確率分布のグラフ を表示するプログラムです。実行結果から、小数点以下第 4 桁で四捨五入すると 平均が 0、標準偏差が 1.04 の離散型確率分布が計算できていることがわかります。なお、連続型確率分布から離散型確率分布を計算する場合は、どうしても誤差が発生して 標準偏差が少しだけずれてしまう ので 1 にはなりませんが、1.04 なので ほぼ 1 になっている ことが確認できます。

pdist = calc_discrete_ndist(0, 1, 10)
print(calc_stval(pdist))
draw_pdist(pdist, label="平均=0, 標準偏差=1")

実行結果

(1.1102230246251565e-16, 1.0833333223611192, 1.0408329944621852)

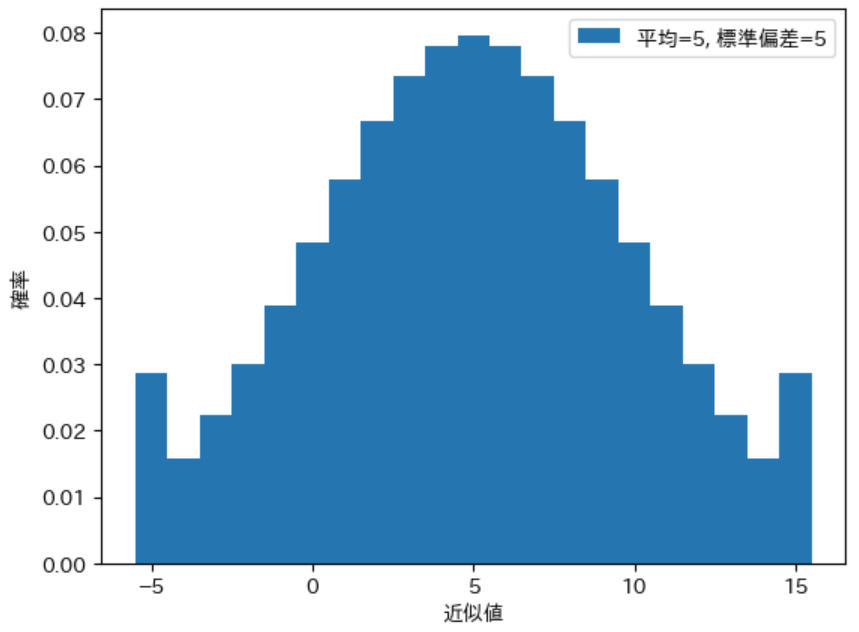
下記のプログラムは 平均が 5、標準偏差が 5、確率変数の範囲を 10 とした場合の正規分布に従う離散型確率分布を計算します。calc_pdict は 両端の確率変数に対する確率 として、その 確率変数以下（または以上）の範囲 の確率を計算するため、両端の確率が他よりも高く計算 されてしまいます。そのため、実行結果の確率分布の図からわかるように、標準偏差を 5 にすると、 両端がおかしな形になる ことがわかります。また、標準偏差 も 4.69 のように 5 から離れた値 になっています。

pdist = calc_discrete_ndist(5, 5, 10)
print(calc_stval(pdist))
draw_pdist(pdist, label="平均=0, 標準偏差=5")

実行結果

(5.054260696265926, 22.016883005931323, 4.692215149151979)

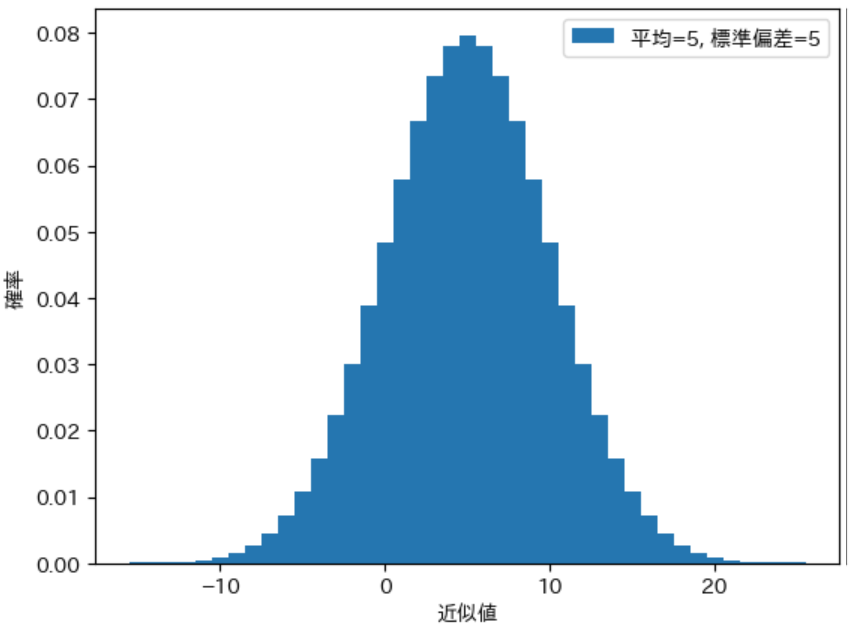
この問題は、両端の付近の確率変数に対する確率 が ある程度以上小さければ ほとんど 目立たなくなります。上記の場合は下記のプログラムのように 確率変数の範囲を 20 に増やす ことで両端の確率が大きいことがわからなくなります。また、標準偏差 は 5.01 と ほぼ 5 が計算 されており、確率分布の グラフもきれいな形になる ことが確認できます。

pdist = calc_discrete_ndist(5, 5, 20)
print(calc_stval(pdist))
draw_pdist(pdist, label="平均=0, 標準偏差=5")

実行結果

(5.000411582556574, 25.069427605637735, 5.006937947052843)

`calc_pdist` での利用

今回の記事の最初で行った下図の max ノード N の近似値のミニマックス値の確率分布の計算を、静的評価関数が 標準偏差が 5 の正規分布 に従う離散型確率分布で近似値の計算を行う場合で計算することにします。

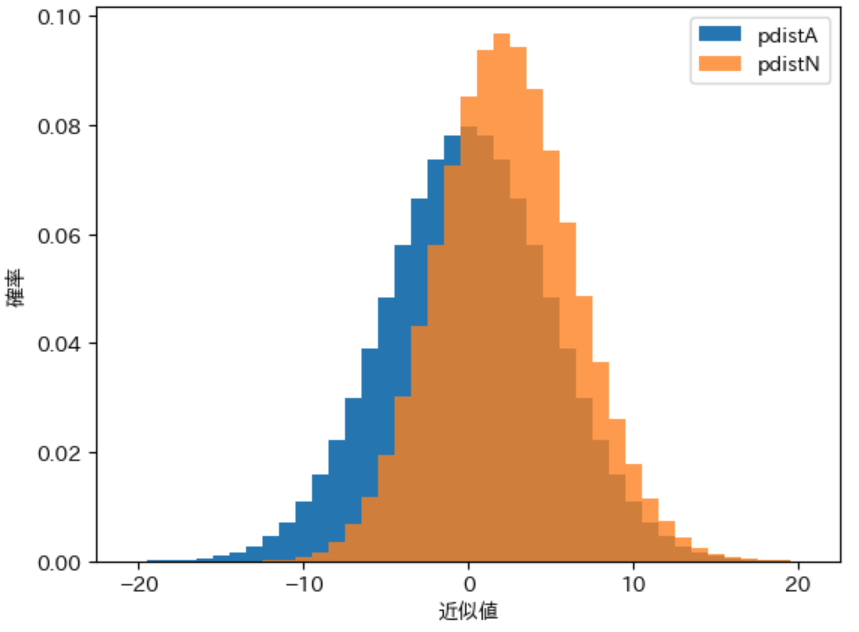
下記はその計算を行うプログラムです。実行結果から 平均が 0 から 2.35 に増える 一方で、標準偏差が 5 から 4.15 に減る ことが確認できます。また、グラフからオレンジ色のグラフが 右にずれて平均が増え、幅が狭く なり ばらつき（標準偏差）が減る こと確認できます。

pdistA = calc_discrete_ndist(0, 5, 20)
pdistB = calc_discrete_ndist(-1, 5, 20)
pdistN = calc_pdist([pdistA, pdistB], maxnode=True)
print(calc_stval(pdistN))
draw_pdist(pdistA, label="pdistA")
draw_pdist(pdistN, alpha=0.8, label="pdistN")

実行結果

(2.349041216719883, 17.213367568249353, 4.148899561118508)

今回の記事のまとめ

今回の記事では calc_pdist の改良を行い、draw_pdist を定義して確率分布の視覚化を行うことができるようにしました。また、正規分布について説明し、正規分布に従う離散型確率変数を計算する関数を定義しました。

本記事で入力したプログラム

今回の記事で定義した draw_pdist と calc_discrete_ndist は tree.py に保存することにします。

リンク	説明
marubatsu.ipynb	本記事で入力して実行した JupyterLab のファイル
tree.py	本記事で更新した tree_new.py

次回の記事

本記事ではまだ紹介していない numpy というモジュールの arange という関数を利用することで、実数に対して規則正しく増えていくような処理をより簡潔に記述することができます ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Pythonで〇×ゲームのAIを一から作成する その177 正規分布に従う離散型確率分布の計算

目次と前回の記事

これまでに作成したモジュール

用語と記号

平均値と期待値の用語について

calc_pdist の改良

確率分布の視覚化

draw_pdist の定義

draw_pdist の改良

正規分布に従う離散型確率分布の作成

正規分布とは何か

離散型確率分布と連続型確率分布

離散型確率分布

連続型確率分布

確率密度関数の意味

累積分布関数

正規分布と標準偏差の関係

正規分布を扱う NormalDist クラス

確率密度関数を計算する pdf メソッド

確率密度関数を計算する cdf メソッド

正規分布に従う離散型確率分布の計算

calc_pdist での利用

今回の記事のまとめ

本記事で入力したプログラム

次回の記事

Pythonで〇×ゲームのAIを一から作成する　その177　正規分布に従う離散型確率分布の計算

`calc_pdist` の改良

`draw_pdist` の定義

`draw_pdist` の改良

確率密度関数を計算する `pdf` メソッド

確率密度関数を計算する `cdf` メソッド

`calc_pdist` での利用