LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@ysgeso

Pythonで〇×ゲームのAIを一から作成する　その178　深さの上限を 1 としたミニマックス法で計算される確率分布の性質

Posted at

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

リンク 説明
marubatsu.py Marubatsu、Marubatsu_GUI クラスの定義
ai.py AI に関する関数
test.py テストに関する関数
util.py ユーティリティ関数の定義
tree.py ゲーム木に関する Node、Mbtree クラスなどの定義
gui.py GUI に関する処理を行う基底クラスとなる GUI クラスの定義

AI の一覧とこれまでに作成したデータファイルについては、下記の記事を参照して下さい。

用語と記号

今回の記事でも前回の記事に引き続き下記の表の用語と記号を用いることにします。

ただし、今回の記事から、ノード $\boldsymbol{X}$ の局面の形勢判断の難しさ を表す $\boldsymbol{d_X}$ と、深さの上限を $\boldsymbol{u}$ とするミニマックス法が計算する 近似値の平均値 と 標準偏差 を表す $\boldsymbol{M(d, u)}$ と $\boldsymbol{S(d, u)}$、ノード $X$ の確率密度関数と確率質量関数を表す $\boldsymbol{P_X}$ と $\boldsymbol{F_X}$ を 新たに追加 することにしました。それぞれの説明は今回の記事で行います。

静的評価関数が計算する近似値 は 深さの上限を 0 としたミニマックス法とみなすことができるので、$\boldsymbol{M(d) = M(d, 0)}$、$\boldsymbol{S(d) = S(d, 0)}$ となります。

用語と記号 意味
正確なミニマックス値 深さの制限がないゲーム木の探索によって計算される、局面の正確なミニマックス値のこと
近似値 静的評価関数が計算する 正確なミニマックス値とは異なる 不正確な値が計算される場合がある 評価値のこと
近似値のミニマックス値 深さ制限探索 によって計算される、静的評価関数が計算する 近似値に対するミニマックス値 のこと
$\boldsymbol{d}$ 局面の形勢判断の難しさ を表す数値
$\boldsymbol{d_X}$ ノード $X$ の局面の形勢判断の難しさ
$\boldsymbol{N(d)}$ 局面の形勢判断の難しさが $d$ の 局面の集合
$\boldsymbol{M(d)}$ $N(d)$ の局面に対して 静的評価関数 が計算する 近似値の平均値
$\boldsymbol{S(d)}$ $N(d)$ の局面に対して 静的評価関数 が計算する 近似値の標準偏差（standard variation）
$\boldsymbol{M(d, u)}$ $N(d)$ の局面に対して深さの上限を $u$ とする ミニマックス法 が計算する 近似値の平均値
$\boldsymbol{S(d, u)}$ $N(d)$ の局面に対して深さの上限を $u$ とする ミニマックス法 が計算する 近似値の標準偏差
$\boldsymbol{N_{mean}(s)}$ $M(d) = s$ となる局面の集合。静的評価関数の ばらつきをなくした場合 にその局面に対して 計算される近似値 が $s$ となる局面の集合　
$\boldsymbol{P_X}$ ノード $X$ の 確率質量関数　
$\boldsymbol{F_X}$ ノード $X$ の 累積分布関数　

深さの上限を 1 としたミニマックス法で計算される確率分布の性質

前回の記事では、下記の設定で 深さの上限を 1 としたミニマックス法での ノード $\boldsymbol{N}$ の近似値のミニマックス値の 確率分布の計算 を行いました、

  • 静的評価関数が任意の $d$ に対して平均が $M(d)$、標準偏差が 5 の正規分布に従う確率分布で近似値を計算する
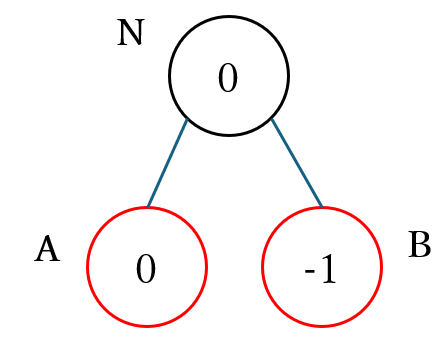
  • max ノードであるノード $N$ が下図のように子ノード $A$ と $B$ を持つ。なおノードの黒枠が max ノードを、赤枠が min ノードを表す
  • ノード $A$ と $N$ は $N_{mean}(0)$、ノード $B$ は $N_{mean}(-1)$ の集合に属する。図のノードの中の数値がそのノードが属する $N_{mean}(s)$ の集合の $s$ を表す

　

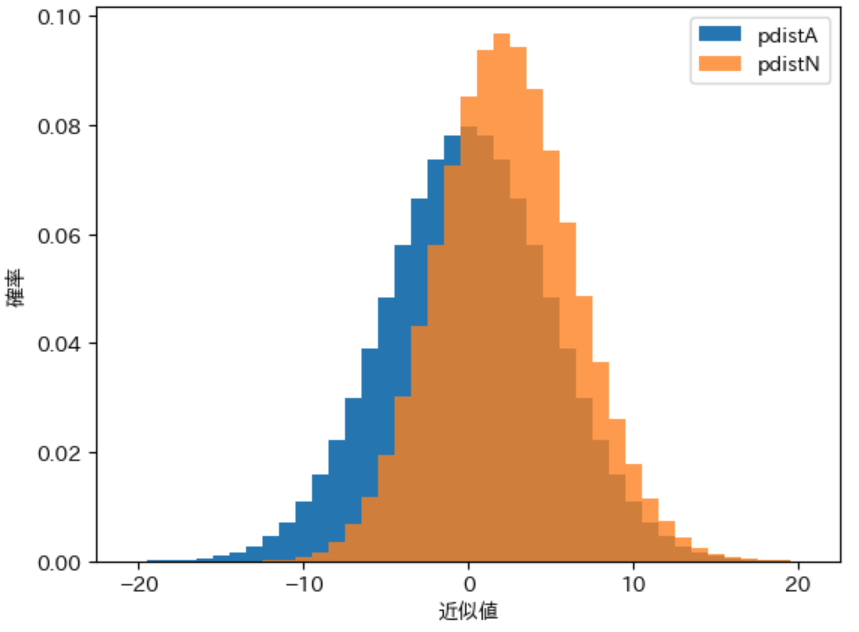
その結果、同じ $N_{mean}(0)$ の集合に属するノード $N$ の近似値のミニマックス値の確率分布と、ノード $A$ の近似値の確率分布の平均と標準偏差を比べると、下記の表のようにノード $\boldsymbol{N}$ の確率分布のほうが 平均値が高く、標準偏差が小さく なるという結果が得られました。

平均 標準偏差
ノード $A$ 0.00 5.01
ノード $N$ 2.35 4.15

下記はノード $A$ と ノード $N$ の 確率分布をグラフ化 した図で、図からもノード $N$ のほうが明らかに平均が高く、幅が狭いことから標準偏差が小さくなることがわかります。

今回の記事では、上記のようなことが起きる理由について説明します。

条件の設定

下記は検証を行う際の 前提条件 です。なお、$N$ が min ノードの場合は max ノードと正負が反転する以外は同様の性質を持つので説明を省略します。

  • 静的評価関数が任意の $d$ に対して同一の標準偏差 $σ$ の正規分布に従う確率分布で近似値を計算する
  • max ノードであるノード $N$ が 2 つ以上の複数の子ノード $A$、$B$、$C$・・・ を持つ
  • それぞれの子ノードの局面の難しさを $d_A$、$d_B$、$d_C$ ・・・ のように表記した場合に、$M(d_A) ≧ M(d_B) ≧ M(d_C) ・・・$ の条件を満たすものとする。別の言葉で説明すると、ノード $\boldsymbol{A}$ に対して計算される 近似値の平均が最も大きい ことを表す
  • $N$ は max ノードなので、$N$ と $A$ の 局面の形勢判断の難しさは同じ（$d_N = d_A$）であるものとする

上記の条件が満たされる場合に、下記の性質が成り立つことを示します。

  • $M(d_N, 1) ≧ M(d_A) = M(d_N, 0)$
  • $S(d_N, 1) ≦ S(d_A) = S(d_N, 0)$

上記の式を言葉で説明すると以下のようになります。

  • $N$ に対して 深さの上限 を 0 と 1 としたミニマックス法で 近似値のミニマックス値 を計算すると、下記の性質が成り立つ
    • 平均 は 深さの上限を 1 としたほうが 同じかより大きく なる
    • 標準偏差 は 深さの上限を 1 としたほうが 同じかより小さく なる

深さの上限を 1 とした場合の平均が増える理由

ミニマックス法では max ノード では子ノードに対して計算された 近似値の最大値 を計算するため、ノード $X$ に対して静的評価関数が計算した近似値を $score(X)$ と表記すると、ノード $\boldsymbol{N}$ に対して計算される 近似値のミニマックス値 は以下の性質を持ちます。

$max(score(A), score(B), score(C), ・・・) ≧ score(A)$

そのため、ノード $\boldsymbol{N}$ に対して計算される 近似値のミニマックス値 は、ノード $\boldsymbol{A}$ に対して静的評価関数が計算する 近似値以上 になります。$d_A = d_N$ という前提条件から $M(d_A) = M(d_N)$ となるので、下記の式が成り立ちます。

$M(d_N, 1) ≧ M(d_A) = M(d_N, 0)$

これが 深さの上限を 1 とした場合の $N$ の確率分布の平均が、上限を 0 とした場合の $N$ の確率分布の 平均以上になる理由 です。

ノード $N$ が min ノードの場合は同様の理由で、 深さの上限を 1 とした場合の平均が、上限を 0 とした場合の 平均以下 になります。

深さの上限を 1 とした場合の標準偏差が減る理由

次に、標準偏差が減る理由 について説明します。そのためには、深さの上限を 1 としたミニマックス法で $N$ に対して計算される近似値のミニマックス値の 確率分布の性質を検証 する必要があります。以後はその確率分布の事を単に $N$ の確率分布と表記することにします。

計算を簡単にするために、最初に $N$ の 子ノードの数が 2 の場合 について説明します。

離散型確率分布 では確率変数 $X$ が $a$ の場合の確率を $P(X=a)$、確率変数 $X$ が $a ≦ X ≦ b$ の場合の確率を $P(a ≦ X ≦ b)$ のように記述します。前回の記事で説明したように、この関数 $P$ を 確率質量関数 と呼び、前回の記事で定義した draw_pdict で表示する 確率分布のグラフ は 確率質量関数のグラフ です。本記事では以後は ノード $\boldsymbol{X}$ の確率質量関数 を $\boldsymbol{P_X}$ と表記することにします。

ノード N の累積分布の計算方法

離散型確率分布でも連続型確率分布と同様に、確率変数 $X$ が $a$ 以下の確率を表す 累積分布関数 $\boldsymbol{F(a) = P(a ≦ X)}$ を考えることができます。本記事ではノード $\boldsymbol{X}$ の累積分布関数 を $\boldsymbol{F_X}$ と表記することにします。

max ノード $N$ が子ノード $A$ と子ノード $B$ を持つ場合に、ノード $\boldsymbol{N}$ を 深さの上限が 1 のミニマックス法で計算した場合の近似値のミニマックス値の 累積分布関数 $\boldsymbol{F_N}$ は、ノード $\boldsymbol{A}$ と ノード $\boldsymbol{B}$ を静的評価関数で計算した場合の 累積分布関数 $\boldsymbol{F_A}$ と $\boldsymbol{F_B}$ を用いた 下記の式で計算 することができます。

$F_N(x) = F_A(x) × F_B(x)$

上記の式で $F_N$ を計算できる理由は、max ノード で行われる計算が 子ノードの中で最も高い近似値を計算 するため、$\boldsymbol{N}$ に対して $\boldsymbol{a}$ 以下の値が計算 される条件は $\boldsymbol{A}$ と $\boldsymbol{B}$ の 両方で $\boldsymbol{a}$ 以下の値が計算 される場合だからです。

累積分布を計算する関数の定義

$N$ の 累積分布が上記の式で計算できること を実際に 確認する ことにします。そのためにはノード $A$ と $B$ の 累積分布を計算する必要 があります。そこで、離散型確率分布を表すデータから 累積分布（cumulative distribution）を計算する下記の calc_cdist という関数を定義することにします。

累積分布のデータ構造 は、確率分布のデータ構造と同様に dict で表現 することにします。

  • 1 行目：離散型確率分布を代入する仮引数 pdist を持つ関数として定義する
  • 2 行目：累積確率を計算する変数を 0 で初期化する
  • 3 行目：累積分布を計算する変数を空の dict で初期化する
  • 4 行目：確率分布のデータから確率変数とその確率を順番に取り出す繰り返し処理を行う
  • 5 行目：累積確率に、取り出した確率変数の確率を加算する
  • 6 行目：累積分布の確率変数のキーの値に累積確率を代入する
  • 7 行目：計算した累積分布を返り値として返る
1  def calc_cdist(pdist):
2      psum = 0
3      cdist = {}
4      for score, p in pdist.items():
5          psum += p
6          cdist[score] = psum
7      return cdist
行番号のないプログラム 
def calc_cdist(pdist):
    psum = 0
    cdist = {}
    for score, p in pdist.items():
        psum += p
        cdist[score] = psum
    return cdist

calc_cdist で累積分布を正しく計算するためには、確率分布を表す dict のキーが、小さい順に登録されている必要がある点に注意が必要です。calc_discrete_ndist や calc_pdist が計算する確率分布はそのような性質を持ちます。

ノード A と B の累積分布の計算

下記の下図の条件でノード $\boldsymbol{A}$ と $\boldsymbol{B}$ の 累積分布を計算 することにします。

  • 前回の記事と同様にノード $A$ と $B$ の $M(d_A) = 0$、$M(d_B) = -1$ とする
  • 静的評価関数が標準偏差が 5 の正規分布に従う確率分布で近似値を計算するものとする

　

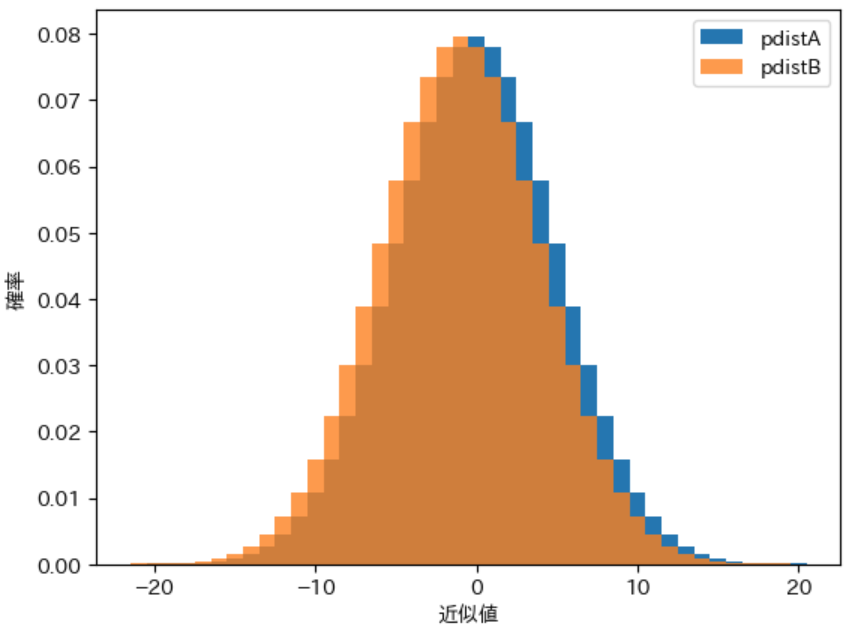
ノード $A$ と $B$ の 確率分布 は前回の記事で定義した calc_discrete_ndist を利用した下記のプログラムで計算できます。また、下記では前回の記事で定義した draw_pdist を利用してグラフ化を行いました。

from tree import calc_discrete_ndist, draw_pdist

pdistA = calc_discrete_ndist(0, 5, 20)
pdistB = calc_discrete_ndist(-1, 5, 20)
draw_pdist(pdistA, label="pdistA")
draw_pdist(pdistB, label="pdistB", alpha=0.8)

実行結果

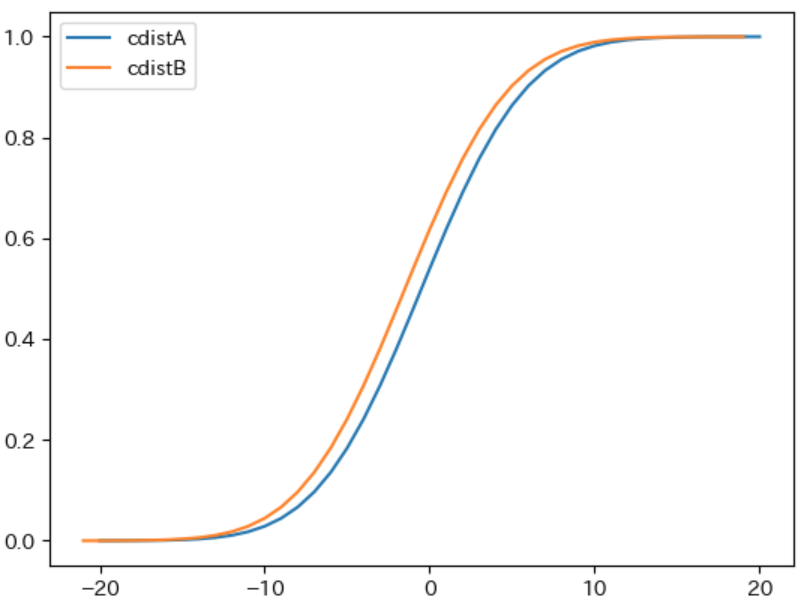
次に、下記のプログラムで先程定義した calc_cdist を利用してそれぞれの 累積分布を計算 し、plot でそれぞれの グラフを描画 します。

import matplotlib.pyplot as plt

cdistA = calc_cdist(pdistA)
cdistB = calc_cdist(pdistB)
plt.plot(cdistA.keys(), cdistA.values(), label="cdistA")
plt.plot(cdistB.keys(), cdistA.values(), label="cdistB")
plt.legend()

実行結果

ノード N の累積分布の計算

次に、ノード $\boldsymbol{N}$ の累積分布 を先程説明した $F_N(x) = F_A(x) × F_B(x)$ という式を利用して下記のプログラムで計算して表示します。

  • 3 行目：ノード $N$ の累積分布を計算する変数を空の dict で初期化する
  • 4 行目：ノード $A$ の累積分布から順番に確率変数と累積確率を取り出して繰り返し処理を行う
  • 5 行目：ノード $A$ とノード $B$ の累積分布を表すデータの両方が確率変数 score を持つ場合に上記の式で $N$ の累積分布の計算を行う
1  from pprint import pprint
2  
3  cdistN = {}
4  for score, p in cdistA.items():
5      if score in cdistA and score in cdistB:
6          cdistN[score] = cdistA[score] * cdistB[score]
7  pprint(cdistN)
行番号のないプログラム 
from pprint import pprint

cdistN = {}
for score, p in cdistA.items():
    if score in cdistA and score in cdistB:
        cdistN[score] = cdistA[score] * cdistB[score]
pprint(cdistN)

実行結果

{-20: 5.184773066333963e-09,
 -19: 2.507735271912644e-08,
 -18: 1.124585130262849e-07,
 -17: 4.677627535178823e-07,
 -16: 1.8053669447171754e-06,
 -15: 6.4687258337963435e-06,
 -14: 2.1528747010115977e-05,
 -13: 6.659313415140906e-05,
 -12: 0.0001915800115891324,
 -11: 0.0005130047016703317,
 -10: 0.0012797667770334997,
 -9: 0.002977293840149786,
 -8: 0.006466969456633866,
 -7: 0.013132540441430791,
 -6: 0.024970712183092304,
 -5: 0.04453586015753854,
 -4: 0.07465486971805763,
 -3: 0.1178886693731333,
 -2: 0.17582652720305386,
 -1: 0.2484137433778345,
 0: 0.3335657866690355,
 1: 0.427262552836099,
 2: 0.5241536787689977,
 3: 0.618512082587706,
 4: 0.7052445258899501,
 5: 0.7806659949094378,
 6: 0.8428592836021654,
 7: 0.8916046298127487,
 8: 0.9279977442024887,
 9: 0.9539320243228522,
 10: 0.9716030494270969,
 11: 0.9831328177866994,
 12: 0.9903448896181933,
 13: 0.9946736816224091,
 14: 0.9971683888533422,
 15: 0.9985494404071513,
 16: 0.9992840592370937,
 17: 0.9996595962648398,
 18: 0.9998441091072781,
 19: 0.9999519036559824}

上記の計算結果が正しいことを、下記のプログラムでノード $N$ の 確率分布 を前回の記事で定義した calc_pdist を利用して計算し、calc_cdist で その累積分布を計算した結果と比較 することにします。

from tree import calc_pdist

pdistN = calc_pdist([pdistA, pdistB])
cdistN2 = calc_cdist(pdistN)
pprint(cdistN2)

実行結果

{-20: 5.184773066333963e-09,
 -19: 2.507735271912644e-08,
 -18: 1.1245851302628488e-07,
 -17: 4.6776275351788217e-07,
 -16: 1.8053669447171752e-06,
 -15: 6.4687258337963435e-06,
 -14: 2.1528747010115974e-05,
 -13: 6.659313415140905e-05,
 -12: 0.00019158001158913238,
 -11: 0.0005130047016703317,
 -10: 0.0012797667770334997,
 -9: 0.002977293840149786,
 -8: 0.006466969456633866,
 -7: 0.013132540441430791,
 -6: 0.024970712183092308,
 -5: 0.04453586015753855,
 -4: 0.07465486971805764,
 -3: 0.1178886693731333,
 -2: 0.17582652720305386,
 -1: 0.2484137433778345,
 0: 0.3335657866690355,
 1: 0.42726255283609904,
 2: 0.5241536787689977,
 3: 0.6185120825877061,
 4: 0.7052445258899502,
 5: 0.7806659949094379,
 6: 0.8428592836021656,
 7: 0.8916046298127488,
 8: 0.9279977442024888,
 9: 0.9539320243228522,
 10: 0.9716030494270969,
 11: 0.9831328177866995,
 12: 0.9903448896181934,
 13: 0.9946736816224092,
 14: 0.9971683888533424,
 15: 0.9985494404071514,
 16: 0.9992840592370938,
 17: 0.9996595962648399,
 18: 0.9998441091072782,
 19: 0.9999519036559825,
 20: 1.0000000000000002}

2 つの 実行結果を比較 すると、多少の誤差はありますが ほぼ同じ累積分布になっている ことが確認できます。また、下記のプログラムで 2 つの累積分布をグラフ化 すると、2 つのグラフが重なって 1 つのグラフのように見えることから、2 つの累積分布がほぼ同じになる ことが確認できます。

plt.plot(cdistN.keys(), cdistN.values(), label="cdistN")
plt.plot(cdistN2.keys(), cdistN2.values(), label="cdistN2")
plt.legend()

実行結果

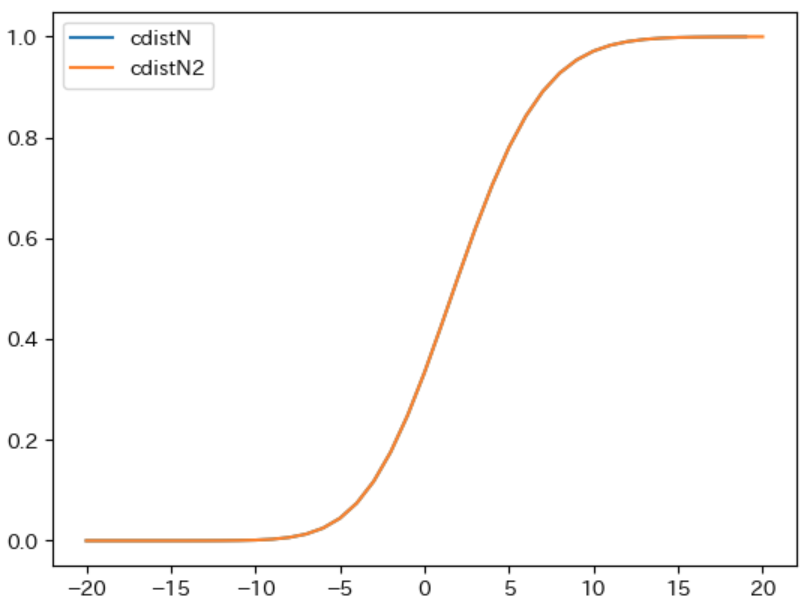
ノード N の累積分布の性質の検証

次に、ノード $\boldsymbol{N}$ の 累積分布の性質を検証 します。下記は、ノード $A$、$B$、$N$ の累積分布のグラフを描画するプログラムです。

plt.plot(cdistA.keys(), cdistA.values(), label="cdistA")
plt.plot(cdistB.keys(), cdistB.values(), label="cdistB")
plt.plot(cdistN.keys(), cdistN.values(), label="cdistN")
plt.legend()

実行結果

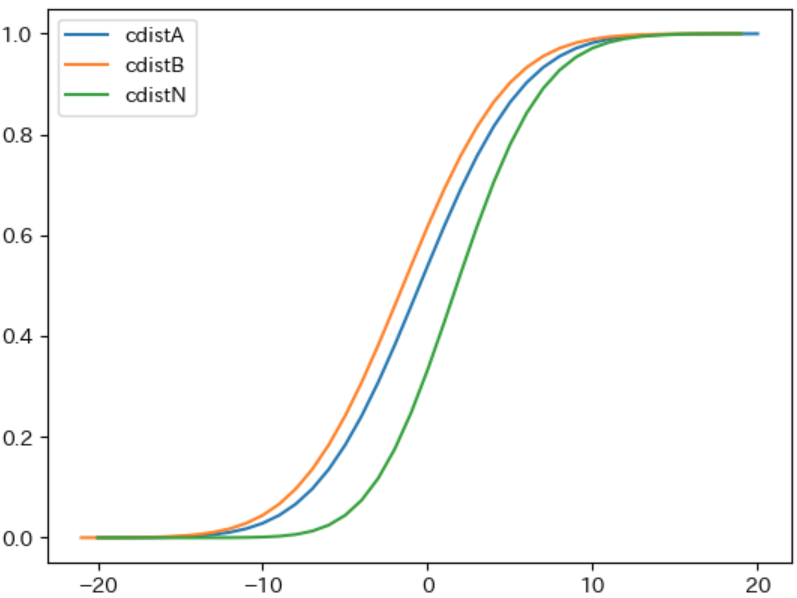
累積分布関数 $\boldsymbol{F(x)}$ の値 は $X ≦ x$ となる 確率を表す のでその値は 0 以上 1 未満、すなわち任意の $x$ に対して $\boldsymbol{0 ≦ F(x) ≦ 1}$ になります。また、$N$ の累積分布関数 $\boldsymbol{F_N(x)}$ は $\boldsymbol{F_N(x) = F_A(x) × F_B(x)}$ という式で計算されるため、必ず $\boldsymbol{F_N(x) ≦ F_A(x)}$ かつ $\boldsymbol{F_N(x) ≦ F_B(x)}$ となります。上記の cdistN のグラフ が、すべての範囲 において cdistA と cdistB より小さくなる のはそのためです。

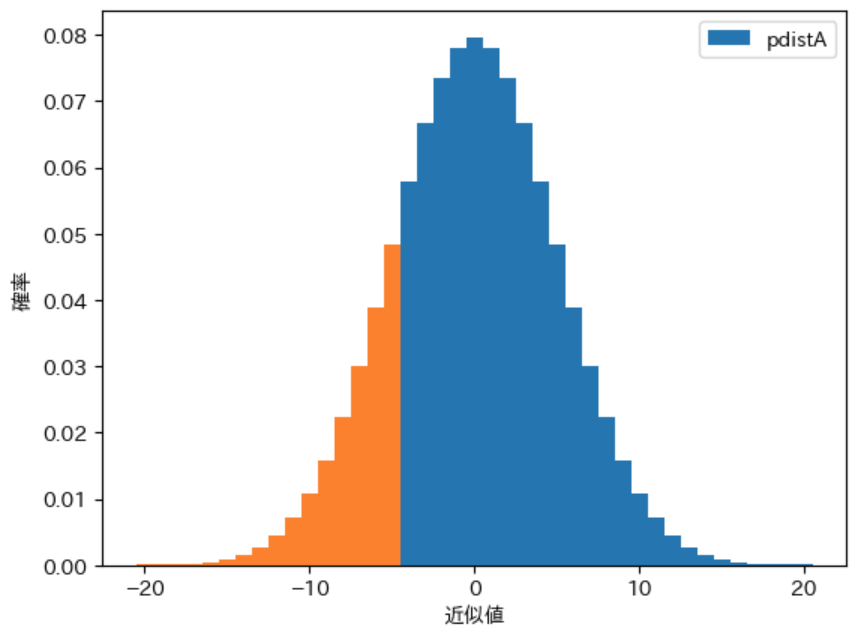
累積分布関数 $\boldsymbol{F(x)}$ は $\boldsymbol{X ≦ x}$ となる確率 を表すので、確率分布のグラフ で $\boldsymbol{X <= x}$ となる部分の 面積 を表します。例えば $\boldsymbol{F_A(-5)}$ は、下図の $A$ の確率分布を表す pdistA の -5 以下 のグラフの オレンジ色で塗りつぶされた部分 の面積を表します。

累積分布関数 は 0 から 1 に 向かって 単調増加 するという性質を持ちます。累積分布関数が 0 から単調増加 することと、すべての $x$ に対して $\boldsymbol{F_N(x) ≦ F_A(x)}$ という性質から $\boldsymbol{x}$ が一定以上小さい場合 は、$\boldsymbol{F_N}$ は $F_A$ と比べて 緩やかに増加 します。増加の度合い は累積分布関数の グラフの傾き によって表され、実際に下記のグラフでは見た目からも明らかに $\boldsymbol{x ≦ -5}$ の範囲 では $\boldsymbol{F_N}$ のグラフを表す緑色の cdistN のほう が $F_A$ のグラフを表す青色の cdistA よりも 傾きが緩やか になっています。

一方、累積分布関数が 1 に向かって単調増加 することと、最初は $F_N$ のほうが $F_A$ よりも緩やかに増加する事から、途中から $\boldsymbol{F_N}$ のほうが $F_A$ と比べて 増加率が高く なります。実際に上記のグラフでは 0 付近から $F_N$ のほうが $F_A$ よりも グラフの傾きが高くなる ことがわかります。

確率変数が整数の値を 取る離散型確率分布の 累積分布関数 $F(x)$ は、先程定義した calc_pdist の中の処理で行ったように、下記の式で計算します。

$F(x) = F(x - 1) + P(x)$

従って、$\boldsymbol{F(x)}$ の $\boldsymbol{x}$ での増加量 を表す グラフの傾き は 確率分布のグラフ の $\boldsymbol{P(x)}$ の値 になります。実際にそのことは、下記のプログラムによって表示されるノード $A$ と ノード $N$ の確率分布のグラフが以下の表のようになることからも確認できます。

x の範囲 確率分布の値
$\boldsymbol{X < 0}$ $P_N(x) < P_A(x)$。pdistA のほうが大きい
$\boldsymbol{0 ≦ X}$ $P_N(x) > P_A(x)$。pdistN のほうが大きい 
draw_pdist(pdistA, label="pdistA")
draw_pdist(pdistN, label="pdistN", alpha=0.8)

実行結果

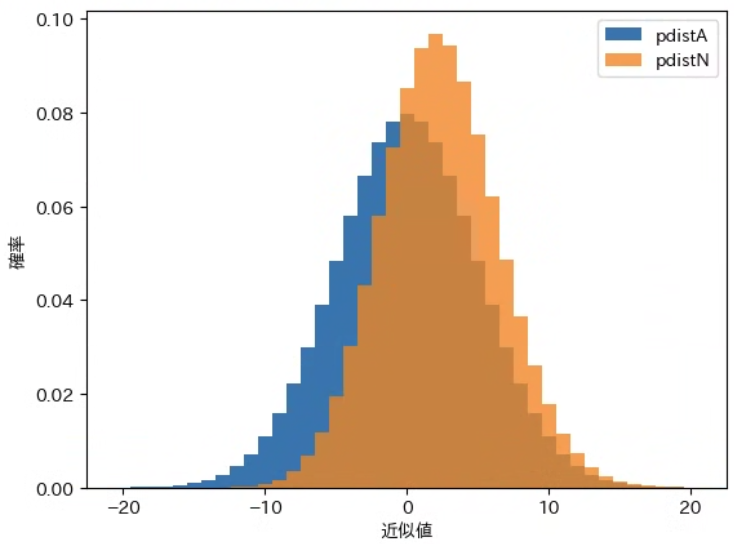
このことから、上図の 確率分布のグラフ と x 軸との間の面積 は、$\boldsymbol{X < 0}$ の範囲では pdistN のほうが小さく 、$\boldsymbol{0 ≦ X}$ の範囲では pdistN のほうが大きく なります。そのため pdistN のグラフは、pdistA のグラフと比べて 右に偏ったグラフ になります。右に偏る ということは 平均が高くなる ということを表します。

上記は離散型確率分布での説明ですが、連続型隔離分布の場合の累積分布関数の傾きは、下記のように確率密度関数で表されることを数学的に説明できます。

前回の記事のノートで説明したように、連続型確率分布の場合の累積分布関数は確率分布のグラフを表す確率密度関数の積分を使って下記のように定義できます。

$F(a) = \int_{-∞}^{a}f(x)dx$

グラフの増加率を表す傾きは微分で計算でき、積分は微分の反対の計算を行うことから、確率密度関数 $f(x)$ は累積分布関数 $F(x)$ の $x$ での傾きを表します。

一方、下図の 累積分布関数のグラフ からわかるように、$\boldsymbol{x}$ がある程度以上大きくなる と $\boldsymbol{F(x)}$ は 1 に急速に近づいていき、その値は ほぼ 1 になります。そのため、x がある程度以上大きくなる と下図のグラフのように $F_N(x)$ と $F_A(x)$ は 急速に近づいていき どちらも ほぼ 1 になります。確率分布 は、累積分布から計算できる ので、$x$ がある程度以上大きくなると $A$ と $N$ の 確率分布のグラフの形状 は ほぼ同じ になります。

実際に下図の確率分布のグラフでは x が 15 以上になるあたり から pdistA と pdistN のグラフは ほぼ同じ形状 になります。

ここまでの検証をまとめると以下のようになります。

  • ノード $\boldsymbol{N}$ の 確率分布のグラフ は、ノード $A$ の確率分布のグラフよりも 右に偏る
  • ノード $A$ と $N$ の確率分布のグラフは $\boldsymbol{x}$ が大きくなる と 形状はほぼ同じ になる

上記の検証結果から $\boldsymbol{N}$ の確率分布のグラフ は $A$ の確率分布のグラフに対して、右端の形状を変えない ように、左から右に押しつぶすような形で変形 させた形になることがわかります。グラフの 形状が x 軸方向に押しつぶされる ことによって 散らばりが減る ことになり、標準偏差が減る ことになります。

子ノードの数が 3 以上の場合

子ノードの数が 3 以上の場合はノード $N$ の累積分布関数は下記の式で計算できます。

$F_N(x) = F_A(x) × F_B(x) × F_C(x) × ・・・$

従って、この場合も $\boldsymbol{F_N(x) ≦ F_A(x)}$ となるため、上記で説明したのと 同じ理由から 子ノードの数が 3 以上の場合も 平均は増え、 標準偏差は減ります。

上記から下記が成り立つことがわかりました。

  • $M(d_N, 1) ≧ M(d_A) = M(d_N, 0)$
  • $S(d_N, 1) ≦ S(d_A) = S(d_N, 0)$

平均の上昇と、標準偏差の減少の意味

平均の上昇 と、標準偏差の減少 の 意味 を別の言葉で説明すると以下のようになります。

確率分布の 平均が大きくなる ということは、形勢判断 を先手にとって有利であると 過大評価する ということを意味します。一方、確率分布の 標準偏差が小さくなる ということは、形勢判断を 大きく誤る可能性が減る ということを意味します。

ミニマックス法で max ノードの計算を行う際に、深さの上限を 0 から 1 とすることで以下のようなことが起きる。

  • 形勢判断を 過大評価 する
  • 形勢判断を 大きく誤る可能性が減る

子ノードの確率分布が与える影響の検証

次に、子ノードの確率分布 が $N$ の確率分布の平均と標準偏差に対して どのように影響するか について検証することにします。

子ノードの確率分布の平均による影響

最初に、子ノード に対して静的評価関数が計算する近似値の 確率分布の平均 が、$N$ の確率分布の 平均と標準偏差 に どのような影響を与えるか について検証することにします。

具体的には 下記の条件 で $N$ の確率分布を計算し、平均と標準偏差がどのように変化するか を確認することにします。計算を簡単にするために子ノードの数を 2 としました。

  • 静的評価関数が任意の $d$ に対して 同一の標準偏差 5 の正規分布に従う確率分布で近似値を計算する
  • max ノード $N$ は 2 つの子ノード $A$ と $B$ を持つ
  • $A$ と $N$ の局面の形勢判断の難しさは同じであるものとする
  • $M(d_A) = 0$ とする
  • $M(d_B)$ の値として -20 ~ 0 まで のそれぞれの場合で計算を行う

下記は、$M(d_B)$ のそれぞれの値に対して $N$ の確率分布を計算し、平均と標準偏差を計算するプログラムです。また、計算した結果を x 軸を $M(d_B)$ としたグラフで表示します。

  • 3 行目：平均が 0、標準偏差が 5 の正規分布に従う $A$ の確率分布を計算する
  • 4 ~ 7 行目：$N$ の平均と標準偏差、ノード $B$ と $N$ の確率分布の一覧を計算する変数を空の dict で初期化する
  • 8 行目：$M(d_B)$ を表す -20 ~ 0 までの整数の繰り返しを計算する
  • 9 行目：平均が meanB、標準偏差が 5 の正規分布に従う確率分布を計算する
  • 10 ~ 15 行目：ノード $N$ の確率分布を計算し、その平均、標準偏差を計算して dict に追加する
  • 17 ~ 20 行目：x 軸をノード $B$ の平均とした場合の $N$ の確率分布の平均と標準偏差を表すグラフを描画する
  • 21、22 行目：$N$ の確率分布の平均と標準偏差の dict を表示する
 1  from tree import calc_stval
 2  
 3  pdistA = calc_discrete_ndist(0, 5, 20)
 4  meandict = {}
 5  stddict = {}
 6  pdistBdict = {}
 7  pdistNdict = {}
 8  for meanB in range(-20, 1):
 9      pdistB = calc_discrete_ndist(meanB, 5, 20)
10      pdistN = calc_pdist([pdistA, pdistB])
11      meanN, varN, stdN = calc_stval(pdistN)
12      meandict[meanB] =meanN
13      stddict[meanB] = stdN
14      pdistBdict[meanB] = pdistB
15      pdistNdict[meanB] = pdistN
16      
17  plt.plot(meandict.keys(), meandict.values(), label="平均")
18  plt.plot(stddict.keys(), stddict.values(), label="標準偏差")
19  plt.xlabel("ノード B の確率分布の平均")
20  plt.legend()
21  pprint(meandict)
22  pprint(stddict)
行番号のないプログラム 
from tree import calc_stval

pdistA = calc_discrete_ndist(0, 5, 20)
meandict = {}
stddict = {}
pdistBdict = {}
pdistNdict = {}
for meanB in range(-20, 1):
    pdistB = calc_discrete_ndist(meanB, 5, 20)
    pdistN = calc_pdist([pdistA, pdistB])
    meanN, varN, stdN = calc_stval(pdistN)
    meandict[meanB] =meanN
    stddict[meanB] = stdN
    pdistBdict[meanB] = pdistB
    pdistNdict[meanB] = pdistN
    
plt.plot(meandict.keys(), meandict.values(), label="平均")
plt.plot(stddict.keys(), stddict.values(), label="標準偏差")
plt.xlabel("ノード B の確率分布の平均")
plt.legend()
pprint(meandict)
pprint(stddict)

実行結果

{-20: 0.004849353925101274,
 -19: 0.007775019739777178,
 -18: 0.012243167984891501,
 -17: 0.01894163609505288,
 -16: 0.02880126089797834,
 -15: 0.043052924369400156,
 -14: 0.06328638641718635,
 -13: 0.09150612423275765,
 -12: 0.13017796459616646,
 -11: 0.18225920113592736,
 -10: 0.2512044222644311,
 -9: 0.34093970949710795,
 -8: 0.45579939532522984,
 -7: 0.6004222519921993,
 -6: 0.7796076887849025,
 -5: 0.9981369313502241,
 -4: 1.2605687213485217,
 -3: 1.5710231644086232,
 -2: 1.932970301744381,
 -1: 2.349041216719883,
 0: 2.8208786580952716}
{-20: 4.998339006918453,
 -19: 4.993257213165605,
 -18: 4.985967960579742,
 -17: 4.9757448511377875,
 -16: 4.9617289059178855,
 -15: 4.9429501315490025,
 -14: 4.918372581075137,
 -13: 4.886967406993842,
 -12: 4.84781616247952,
 -11: 4.800243097377898,
 -10: 4.743970440296667,
 -9: 4.679284790631162,
 -8: 4.607196020513712,
 -7: 4.529562978719391,
 -6: 4.449153755681647,
 -5: 4.369604264958293,
 -4: 4.29524097533325,
 -3: 4.230746996274265,
 -2: 4.180680402985086,
 -1: 4.148899561118508,
 0: 4.13800036480432}

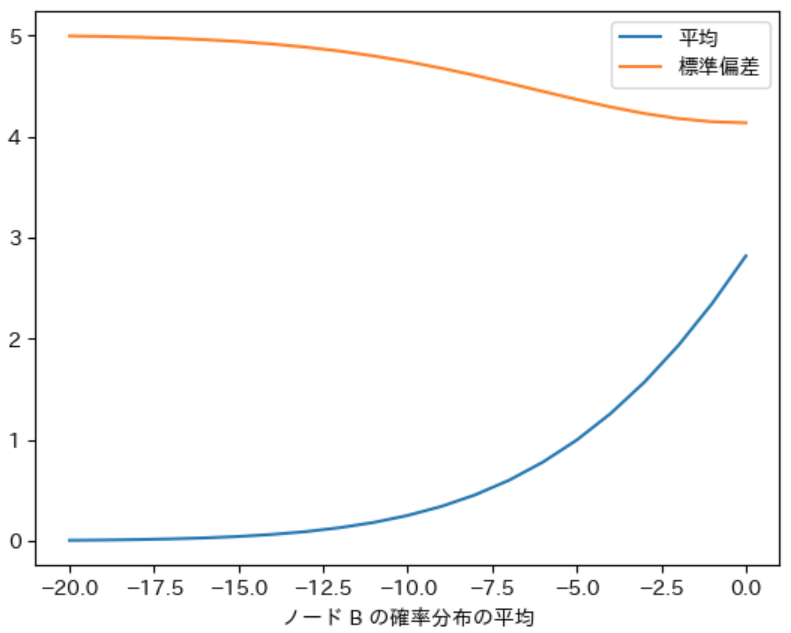
実行結果で表示される数値とグラフから以下の事がわかります。なお、下記の数値は小数点以下第 3 桁で四捨五入しました。

  • 子ノード $B$ の確率分布の平均が -20 の場合は $N$ の確率分布の平均は 0.00、標準偏差は 5.00 となり、$\boldsymbol{N}$ と $\boldsymbol{A}$ の確率分布の 平均と標準偏差 と ほぼ同じ になる
  • 子ノード $B$ の確率分布の 平均が大きくなるにつれて、$\boldsymbol{N}$ の確率分布の 平均が増え、標準偏差が減る

下記は $\boldsymbol{B}$ の確率分布の 平均が -20, -5, 0 の場合の $\boldsymbol{N}$ の確率分布 のグラフを表示 するプログラムです。実行結果のグラフからも上記のようになることが確認できます。

draw_pdist(pdistNdict[-20], label="B の平均 = -20")
draw_pdist(pdistNdict[-5], label="B の平均 = -5", alpha=0.8)
draw_pdist(pdistNdict[0], label="B の平均 = 0", alpha=0.5)

実行結果

!

B の確率分布の平均が -20 の場合の検証

下記は子ノード $\boldsymbol{B}$ の確率分布の 平均が -20 の場合の $\boldsymbol{A}$、$\boldsymbol{B}$、$\boldsymbol{N}$ の 累積確率分布 のグラフを表示するプログラムです。2 本のグラフしか表示されていないように見えるかもしれませんが、これは $\boldsymbol{A}$ と $\boldsymbol{N}$ の 2 つのグラフ の値が ほぼ同じ で 重なっている ため 1 本のグラフのように見える からです。また、グラフの範囲が異なる のは、累積確率分布を表す dict に記録された 確率変数とその確率 が その範囲でのみ計算された からです。範囲外の部分のグラフは左は 0 に、右は 1 になると考えて下さい。

cdistA = calc_cdist(pdistA)
cdistB = calc_cdist(pdistBdict[-20])
cdistN = calc_cdist(pdistNdict[-20])
plt.plot(cdistA.keys(), cdistA.values(), label="cdistA")
plt.plot(cdistB.keys(), cdistB.values(), label="cdistB")
plt.plot(cdistN.keys(), cdistN.values(), label="cdistN")
plt.legend()

実行結果

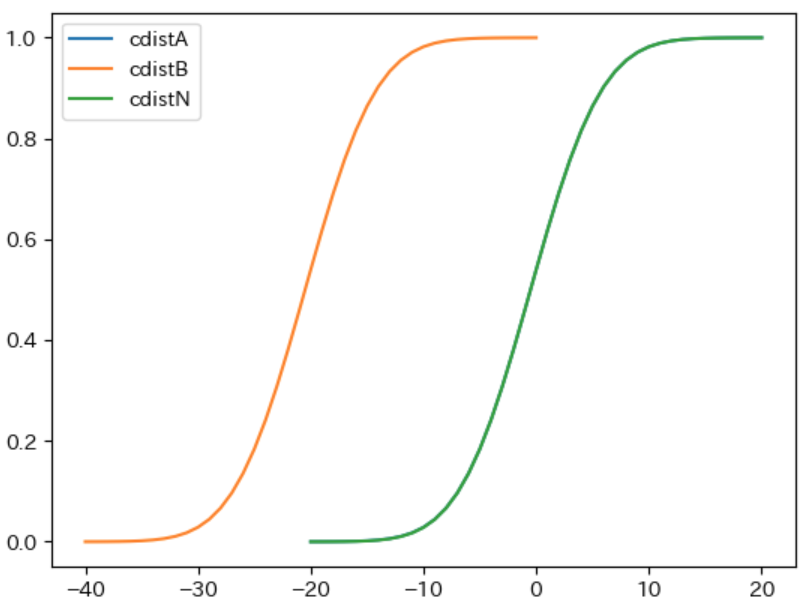
$\boldsymbol{B}$ の確率分布の 平均が -20 の場合に、ノード $A$ と $N$ の 累積分布がほぼ重なる理由 について説明します。

前回の記事で説明したように、正規分布 は 平均 ± 標準偏差 × 2 の範囲 に 全体の約 95 % が入ります。そのため、$\boldsymbol{A}$ の確率分布 である 平均が 0 で 標準偏差が 5 の正規分布では、-5 × 2 = -10 以下 と 5 × 2 = 10 以上 の範囲に 全体の約 5 % が入ります。正規分布は平均を中心とした左右対称となるグラフで表されるので、-10 以下の範囲 と 10 以上の範囲にはそれぞれ 全体の約 2.5 % が入ります。従って $\boldsymbol{x ≦ -10}$ では $\boldsymbol{F_A(x)}$ は 約 0.025 以下 の 0 に近い値 になります。

同様の理由で、$\boldsymbol{B}$ の確率分布 である 平均が -20 で 標準偏差が 5 の正規分布では、-30 以下と、-10 以上の範囲 にそれぞれ 全体の約 2.5 % が入るので、$\boldsymbol{-10 ≦ x}$ では $\boldsymbol{F_B(x)}$ は 1 - 0.025 = 約 0.975 以上 の 1 に近い値 になります。

上記から、以下のようにノード $A$ と $N$ の 累積分布がほぼ重なる理由 が説明できます。

  • $F_N(x) = F_A(x) × F_B(x)$ で計算される
  • 従って $\boldsymbol{F_A(x)}$ が ほぼ 0 である $\boldsymbol{x ≦ -10}$ の範囲では $\boldsymbol{F_N(x)}$ も ほぼ 0 となる
  • 従って $\boldsymbol{F_B(x)}$ が ほぼ 1 である $\boldsymbol{-10 ≦ x}$ の範囲では $\boldsymbol{F_N(x)}$ は ほぼ $\boldsymbol{F_A(x)}$ となる
  • 上記から、すべての範囲 で $\boldsymbol{F_A(x)}$ と $\boldsymbol{F_N(x)}$ は ほぼ同じ になる

$\boldsymbol{F_A(x)}$ と $\boldsymbol{F_N(x)}$ が ほぼ同じ であるということは、ノード $A$ と ノード $N$ の 確率分布 が ほぼ同じ になることを表します。

上記の例のように 同じ標準偏差 の 正規分布 に従う 2 つの確率分布の 平均が大きく離れた場合 は、平均が小さいほう の確率分布で 計算される値 が、平均が大きいほう の確率分布で計算される 値よりも大きくなる確率 が ほぼ 0 になります。そのため、ノード $\boldsymbol{N}$ の確率分布は、ノード $\boldsymbol{A}$ の確率分布と ほぼ同じ になります。

ただし、そのような場合でも平均が減ったり、標準偏差が増えることはありません。

A と B の確率分布の平均の差による影響

2 つの 同じ標準偏差 の 正規分布 に従う確率分布の 平均が近い程、平均が小さいほう の確率分布で 計算される値 が、平均が大きいほうの確率分布で計算される 値よりもよりも大きくなる確率 が 高くなる ため、$\boldsymbol{N}$ の確率分布は $\boldsymbol{A}$ の確率分布よりも 右に偏る ことになります。その結果、平均が上昇 し 標準偏差が減ります。

上記をまとめると以下のようになります。

深さの上限を 0 から 1 とした場合の $N$ の確率分布の 平均と標準偏差 は、2 つの子ノードの確率分布の 平均 によって以下のように影響される。

  • 2 つの子ノードの確率分布の 平均が大きく異なる 場合は、平均も標準偏差も ほとんど変化しない
  • 2 つの子ノードの確率分布の 平均が近い程、平均が大きく標準偏差が小さくなる
  • ただし、どのような場合でも平均が減ったり、標準偏差が増えることはない

上記を別の言葉で説明すると以下のようになります。

子ノードの局面の 形勢が大きく異なる 場合は、先手にとって不利だと思われる局面が 形勢判断に影響することはほとんどない。子ノードの局面の 形勢が似ている 場合は、形勢判断を 過大評価しやすく なるが、一方で形勢判断を 大きく誤る可能性が減る。

子ノードの確率分布の標準偏差による影響

次に、子ノードの確率分布の 標準偏差による影響 を検証することにします。

具体的には 下記の条件 で $N$ の確率分布を計算し、平均と標準偏差がどのように変化するか を確認することにします。

  • 静的評価関数が任意の $d$ に対して同一の標準偏差 $σ$ の正規分布に従う確率分布で近似値を計算する
  • 標準偏差が 1 から 10 まで のそれぞれの場合について計算を行う
  • max ノード $N$ は 2 つの子ノード $A$ と $B$ を持つ
  • $A$ と $N$ の局面の形勢判断の難しさは同じであるものとする
  • $M(d_A) = 0$、$M(d_B) = -1$ とする

下記は上記の処理を行うプログラムです。先ほどのプログラムとほぼ同じなので、異なる部分のみ説明します。

  • 5 行目：ノード $A$、$B$ の標準偏差を表す、1 ~ 10 までの整数の繰り返しを計算する
  • 6、7 行目：ノード $A$ と $B$ に対応する、平均が 0、1、標準偏差が std の正規分布に従う確率分布を計算する
  • 17 行目：$N$ の 標準偏差がどれだけ減ったか がわかるように、ノード $A$ の標準偏差を表すグラフを表示する
 1  meandict = {}
 2  stddict = {}
 3  pdistBdict = {}
 4  pdistNdict = {}
 5  for std in range(1, 11):
 6      pdistA = calc_discrete_ndist(0, std, 20)
 7      pdistB = calc_discrete_ndist(-1, std, 20)
 8      pdistN = calc_pdist([pdistA, pdistB])
 9      meanN, varN, stdN = calc_stval(pdistN)
10      meandict[std] = meanN
11      stddict[std] = stdN
12      pdistBdict[std] = pdistB
13      pdistNdict[std] = pdistN
14      
15  plt.plot(meandict.keys(), meandict.values(), label="N の平均")
16  plt.plot(stddict.keys(), stddict.values(), label="N の標準偏差")
17  plt.plot(stddict.keys(), stddict.keys(), label="A の標準偏差")
18  plt.xlabel("ノード A,B の確率分布の標準偏差")
19  plt.legend()
20  pprint(meandict)
21  pprint(stddict)
行番号のないプログラム 
meandict = {}
stddict = {}
pdistBdict = {}
pdistNdict = {}
for std in range(1, 11):
    pdistA = calc_discrete_ndist(0, std, 20)
    pdistB = calc_discrete_ndist(-1, std, 20)
    pdistN = calc_pdist([pdistA, pdistB])
    meanN, varN, stdN = calc_stval(pdistN)
    meandict[std] = meanN
    stddict[std] = stdN
    pdistBdict[std] = pdistB
    pdistNdict[std] = pdistN
    
plt.plot(meandict.keys(), meandict.values(), label="N の平均")
plt.plot(stddict.keys(), stddict.values(), label="N の標準偏差")
plt.plot(stddict.keys(), stddict.keys(), label="A の標準偏差")
plt.xlabel("ノード A,B の確率分布の標準偏差")
plt.legend()
pprint(meandict)
pprint(stddict)

実行結果

{1: 0.19964358725801898,
 2: 0.6981773244602325,
 3: 1.239368086810338,
 4: 1.7919282435625503,
 5: 2.349041216719883,
 6: 2.907295055180596,
 7: 3.4607716140368128,
 8: 3.999398471809786,
 9: 4.5118781677832205,
 10: 4.989220813077225}
{1: 0.9186033818628424,
 2: 1.7022645013283473,
 3: 2.5115596731001184,
 4: 3.3287207269535593,
 5: 4.148899561118508,
 6: 4.966554448384215,
 7: 5.767438587105039,
 8: 6.531374026619168,
 9: 7.241947019587376,
 10: 7.891114373050852}

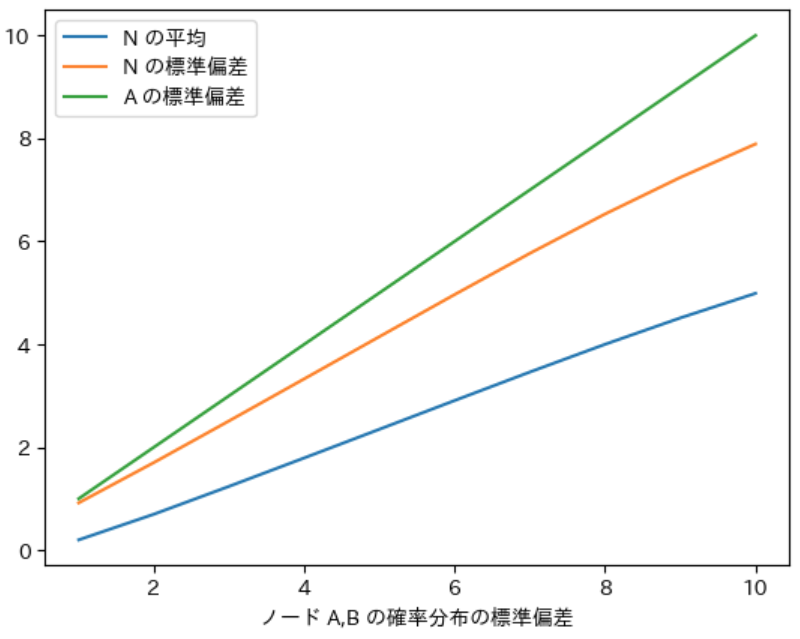
実行結果からノード $\boldsymbol{A}$、$\boldsymbol{B}$ の確率分布の 標準偏差が大きくなるほど ノード $\boldsymbol{N}$ の確率分布の 平均が増える ことが確認できます。これは、静的評価関数の 標準偏差が大きくなるほど 平均よりも 大きな近似値を計算する確率が高い ため 平均の増え幅が大きくなる からです。

$\boldsymbol{N}$ の標準偏差 に関しては、いずれの場合 も緑のグラフのノード $\boldsymbol{A}$ の標準偏差よりも減少する ことと、$\boldsymbol{A}$ の標準偏差が 大きいほど減少幅も大きくなる ことが確認できます。

また、何れの場合でも平均が減ったり、標準偏差が増えることがないことも確認できます。

深さの上限を 0 から 1 とした場合の $N$ の確率分布の 平均と標準偏差 は、2 つの子ノードの確率分布の 標準偏差 によって以下のように影響される。

  • 2 つの子ノードの確率分布の 標準偏差が大きいほど、平均が大きく なる
  • 2 つの子ノードの確率分布の 標準偏差が大きいほど、標準偏差の減り幅 が 大きくなる
  • ただし、どのような場合でも平均が減ったり、標準偏差が増えることはない

上記を別の言葉で説明すると以下のようになります。

現在の局面だけから形勢判断を行うよりも、現在の局面に対して合法手を着手した 複数の局面から形勢判断を行う ことで形勢判断を 大きく誤る可能性が減る。一方で、現在の局面だけから形勢判断を行う場合 に形勢判断を 大きく誤る可能性が高い場合 は形勢判断を 過大評価しやすく なる。

子ノードの数による影響

ここまでの検証では、計算を簡単に行えるように子ノードの数を 2 としてきましたが、実際には子ノードの数は 2 であるとは限りません。そこで次は 子ノード の数による影響を検証することにします。

具体的には 下記の条件 で $N$ の確率分布を計算し、平均と標準偏差がどのように変化するか を確認することにします。

  • 静的評価関数が任意の $d$ に対して同一の標準偏差 5 の正規分布に従う確率分布で近似値を計算する
  • max ノード $N$ は 1 つ以上の子ノード $A$、$B$、$C$、・・・を持つ
  • 子ノードの数 が 1 ~ 5 のそれぞれの場合に対する計算を行う
  • $A$ と $N$ の局面の形勢判断の難しさは同じであるものとする
  • $A$ 以外の全ての子ノードの形勢判断の難しさは同じであるものとする
  • $M(d_A) = 0$、$M(d_B) = -1$ とする

なお、子ノードの数を 1 ~ 5 とした理由は、子ノードの数を 1 増やすごとに product で計算する 直積の集合の数が約 40 倍1 になるため、子ノードの数を 5 以上とした場合 に 処理時間が長くなりすぎる からです。

下記は上記の処理を行うプログラムです。先ほどのプログラムとほぼ同じなので、異なる部分のみ説明します。

  • 5、6 行目：ノード $A$ と $B$ に対応する、平均が 0、1、標準偏差が 5 の正規分布に従う確率分布を計算する
  • 7 行目：$\boldsymbol{A}$ 以外の子ノードの数 を表す 0 ~ 4 までの整数の繰り返しを計算する
  • 8 行目：$\boldsymbol{A}$ 以外の子ノード の 確率分布 は $\boldsymbol{B}$ の確率分布と同じ なので、$A$ の確率分布と num 個の $\boldsymbol{B}$ の確率分布 を要素として持つ list を calc_pdist で計算することで、子ノードの確率分布の直積を計算する
  • 10 ~ 13 行目：子ノードの数は num + 1 なので、dict の num + 1 のキーの値に計算したデータを代入する
 1  meandict = {}
 2  stddict = {}
 3  pdistBdict = {}
 4  pdistNdict = {}
 5  pdistA = calc_discrete_ndist(0, 5, 20)
 6  pdistB = calc_discrete_ndist(-1, 5, 20)
 7  for num in range(0, 5):
 8      pdistN = calc_pdist([pdistA] + [pdistB] * num)
 9      meanN, varN, stdN = calc_stval(pdistN)
10      meandict[num + 1] = meanN
11      stddict[num + 1] = stdN
12      pdistBdict[num + 1] = pdistB
13      pdistNdict[num + 1] = pdistN
14      
15  plt.plot(meandict.keys(), meandict.values(), label="平均")
16  plt.plot(stddict.keys(), stddict.values(), label="標準偏差")
17  plt.xlabel("子ノードの数")
18  plt.legend()
19  pprint(meandict)
20  pprint(stddict)
行番号のないプログラム 
meandict = {}
stddict = {}
pdistBdict = {}
pdistNdict = {}
pdistA = calc_discrete_ndist(0, 5, 20)
pdistB = calc_discrete_ndist(-1, 5, 20)
for num in range(0, 5):
    pdistN = calc_pdist([pdistA] + [pdistB] * num)
    meanN, varN, stdN = calc_stval(pdistN)
    meandict[num + 1] = meanN
    stddict[num + 1] = stdN
    pdistBdict[num + 1] = pdistB
    pdistNdict[num + 1] = pdistN
    
plt.plot(meandict.keys(), meandict.values(), label="平均")
plt.plot(stddict.keys(), stddict.values(), label="標準偏差")
plt.xlabel("子ノードの数")
plt.legend()
pprint(meandict)
pprint(stddict)

実行結果

{1: -3.3306690738754696e-16,
 2: 2.349041216719883,
 3: 3.593424430236882,
 4: 4.423356286724643,
 5: 5.038954187424833}
{1: 5.008033887946253,
 2: 4.148899561118508,
 3: 3.7610731687081422,
 4: 3.526687428469222,
 5: 3.3647613731461354}

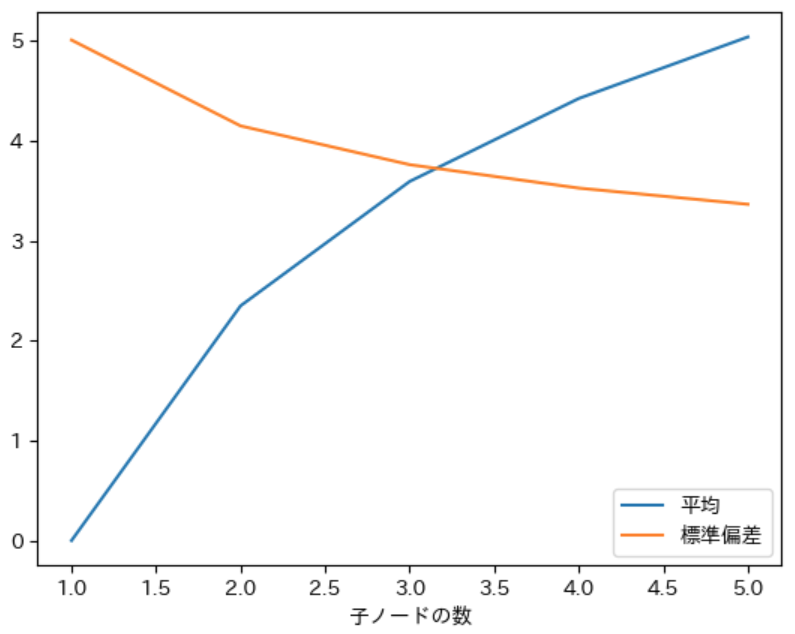
実行結果から、子ノードの数 が 多くなるほど $N$ の確率分布の 平均が大きくなり、標準偏差が小さくなる ことが確認できました。また、当たり前ですが 子ノードの数が 1 の場合はノード $A$ のみが子ノードとなるので $\boldsymbol{N}$ の確率分布は $\boldsymbol{A}$ と同じになる ため平均は 0、標準偏差は 5 になります。

深さの上限を 0 から 1 とした場合の $N$ の確率分布の 平均と標準偏差 は、子ノードの 数 によって以下のように影響される。

  • 子ノードの 数が多いほど、平均が大きく なる
  • 子ノードの 数が多いほど、標準偏差が小さく なる
  • ただし、どのような場合でも平均が減ったり、標準偏差が増えることはない

上記を別の言葉で説明すると以下のようになります。

子ノードの数が多くなるほど、より多くの局面 から 総合的な形勢判断を行う ことができるようになるので、形勢判断を 大きく誤る可能性が減る が、一方で形勢判断を 過大評価しやすくなる。

今回の記事のまとめ

今回の記事では以下の条件を設定しました。

  • 静的評価関数が任意の $d$ に対して同一の標準偏差 $σ$ の正規分布に従う確率分布で近似値を計算する
  • max ノードであるノード $N$ が 2 つ以上の複数の子ノード $A$、$B$、$C$・・・ を持つ
  • それぞれの子ノードの局面の難しさを $d_A$、$d_B$、$d_C$ ・・・ のように表記した場合に、$M(d_A) ≧ M(d_B) ≧ M(d_C) ・・・$ の条件を満たすものとする。別の言葉で説明すると、ノード $\boldsymbol{A}$ に対して計算される 近似値の平均が最も大きい ことを表す
  • $N$ は max ノードなので、$N$ と $A$ の 局面の形勢判断の難しさは同じ（$d_N = d_A$）であるものとする

そして、上記の条件が満たされる場合に、下記の性質が成り立つことを示しました。

  • $N$ に対して 深さの上限 を 0 と 1 としたミニマックス法で 近似値のミニマックス値 を計算すると、下記の性質が成り立つ
    • 平均 は 深さの上限を 1 としたほうが 同じかより大きく なる
    • 標準偏差 は 深さの上限を 1 としたほうが 同じかより小さく なる

上記を式で表すと下記のようになります。

  • $M(d_N, 1) ≧ M(d_N, 0)$
  • $S(d_N, 1) ≦ S(d_N, 0)$

また、子ノードの平均、標準偏差、個数が $N$ の確率分布の平均と標準偏差に与える影響について検証し、以下の性質があること示しました。

深さの上限を 0 から 1 とした場合の $N$ の確率分布の 平均と標準偏差 は、子ノードの確率分布の 平均、標準偏差、子ノードの 数 が以下のような場合に、平均が増え、標準偏差が減る

  • 子ノード $A$ の確率分布の平均により近い子ノードが存在する
  • 子ノードの確率分布の標準偏差が大きい
  • 子ノードの数が多い

ただし、平均が減ったり、標準偏差が増えることはない。

なお、今回の記事では 限られた条件 での検証しか行っていないので、余裕と興味がある方は例えば平均と標準偏差の両方を変化させるなどの他の様々な条件で $N$ の確率分布の平均と標準偏差がどのように変化するかについて検証してみて下さい。

次回の記事では深さの上限を 2 以上にした場合の検証を行います。

本記事で入力したプログラム

今回の記事で定義した calc_cdist は tree.py に保存することにします。

リンク 説明
marubatsu.ipynb 本記事で入力して実行した JupyterLab のファイル
tree.py 本記事で更新した tree_new.py

次回の記事

近日公開予定です

  1. 標準偏差を 5 とした場合の確率分布の確率変数を平均から 20 の範囲で計算したので、計算した確率変数の数は 20 × 2 + 1 = 41 個となるので約 40 倍になります ↩

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?