- RGB ビット深度のうんちく (前編) 〜 前提知識
- RGB ビット深度のうんちく (中編) 〜 実数型と整数型の変換
- RGB ビット深度のうんちく (後編) 〜 整数型同士の変換
はじめに
このエントリは、連続的なRGB値と不連続なRGB値の相互変換についての、うんちくです。
例えば、ガンマ補正は 0.0〜1.0 に対する式なので、RGB値が 0〜255 の場合は 0.0〜1.0 に一度変換する必要があります。
連続的な値のどの範囲を、どの不連続な値で代表させるかは色んなパターンが考えられるので、整理していきます。
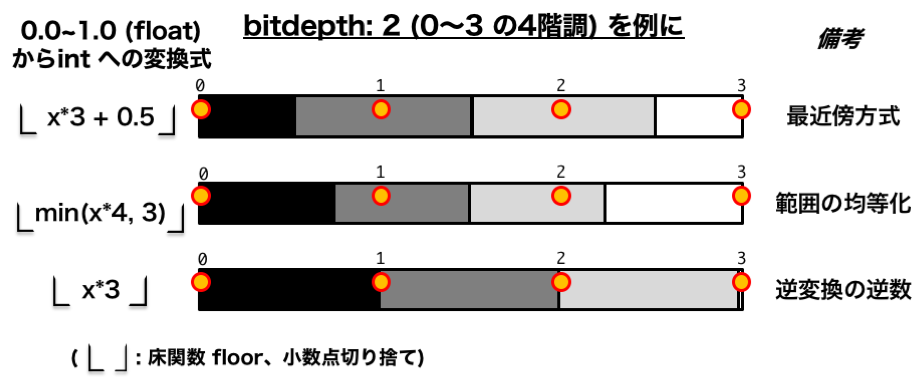
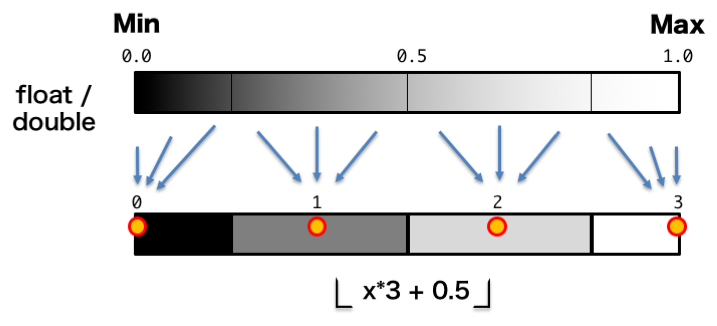
最近傍方式
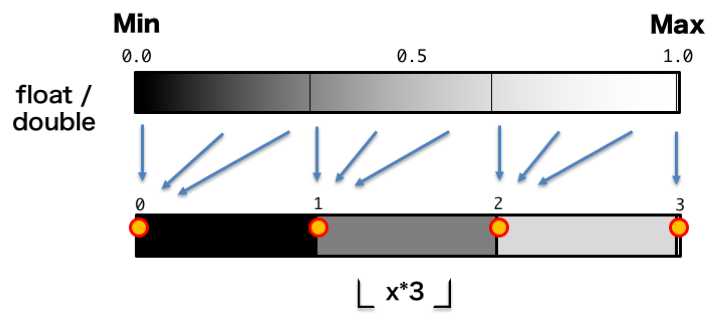
画像処理の世界で実際に使う輝度の量子化はこの方式が基本です。
全体として量子化誤差による輝度のバイアスが少ない傾向があります。つまり、元の画像の明るさを維持しやすいです。
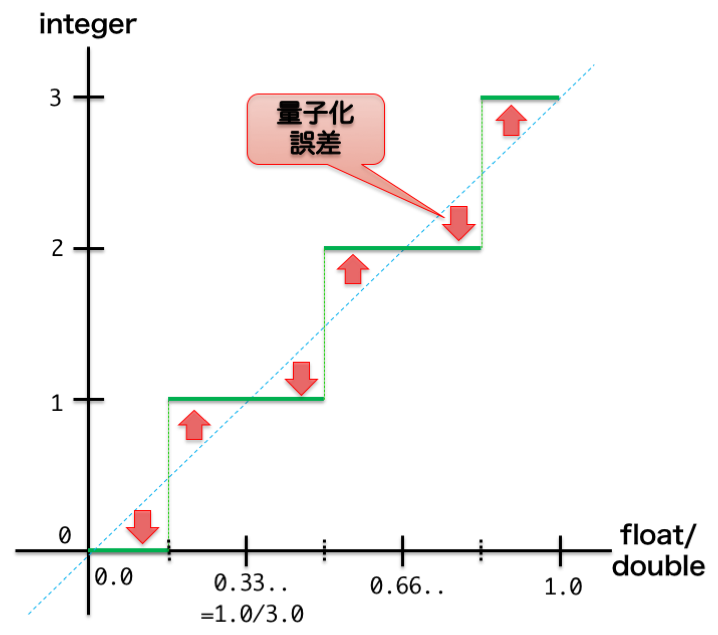
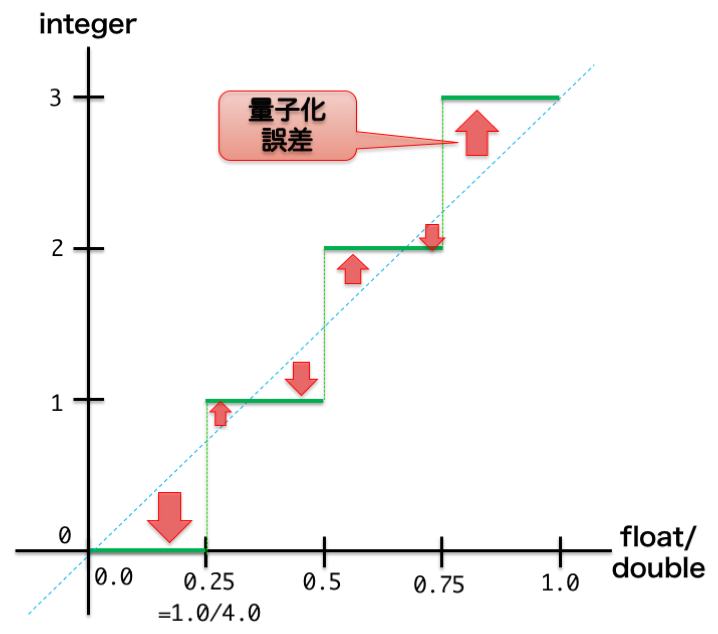
水色の斜めの点線は連続量そのものを表し、緑色は量子化したデジタル値を表します。
このように一定範囲を不連続な値(0,1,2,3)に代表させる為、元の値からずれる分を**量子化誤差(Quantization Error)**と呼びます。
この方式だと量子化誤差の一番大きい場所も抑えられますし、全体としても増分と減分が相殺して良い感じです。
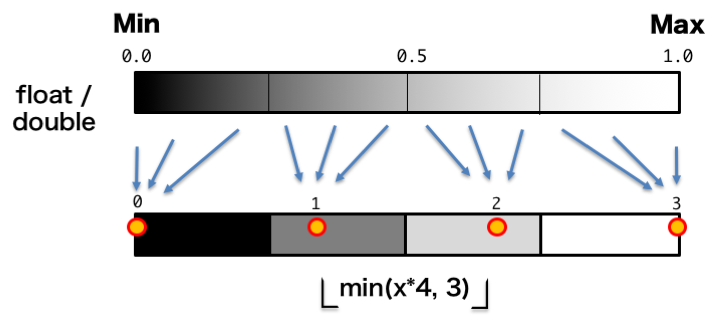
範囲の均等化
量子化の情報量としての考え方では、元のアナログ量をどれだけ均等にコード化出来るかが重要なポイントなので、両端だけ範囲が狭いのは符号化効率的に駄目という判断もあるかもしれません。
量子化誤差の増分と減分が相殺しているように見えますが、、最低輝度と最高輝度の誤差が大きくなります
ただし、中くらいの輝度が広がりそこだけコントラストが改善されます。
実は、デジタルの整数値同士の深度変換だとビット処理の都合で、この方式を使う可能性があります。
それについては、。RGB ビット深度のうんちく (後編)で解説する予定です。
逆変換の逆数
筋の悪い方法ですが、一応把握しておく必要があります。
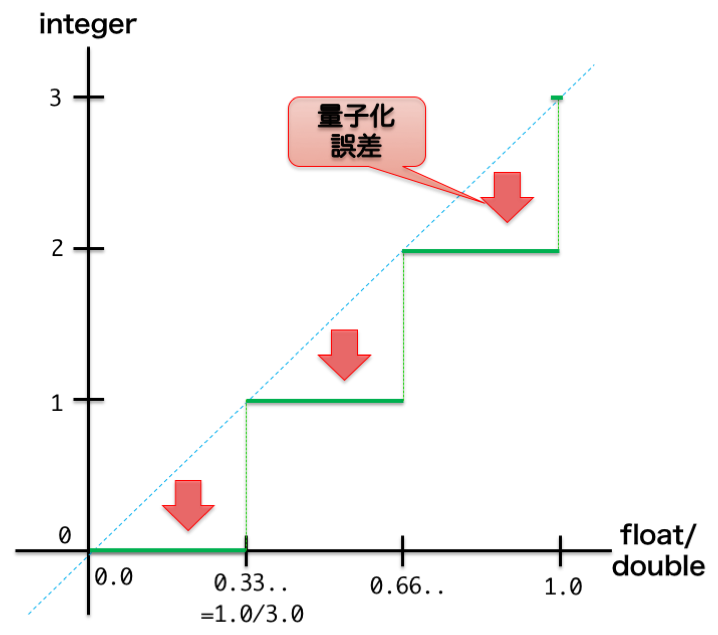
デジタルのビット深度2(0,1,2,3)からアナログに変換する時は、3で割れば良いので、その逆で 3 を掛ければ良いだろうと短絡的な処理を書く事も十分あり得る事です。(整数変換で小数点が落ちる事を忘れてとか。。)
このように暗くなる傾向があります。
実際のところビット深度が多いほど量子化誤差を無視して良い状況が増えるので、処理速度重視でこの方式をあえて使う場面もあるでしょう。
こういう処理をされる可能性を頭に入れておくと、出所の分からない画像を解析する時に役に立つと思います。
また、量子化とは違うのですが、8, 16 しか対応してない画像フォーマットで 12ビットを格納したい時に、16ビットの上位12ビットを使う決まりにした場合、この方式で計算する事になります。PNG の sBIT チャンクまさにそれです。
- 参考) ImageMagick で PNG の形式を変換 #sBIT
デジタルからアナログへ (D/A 変換)
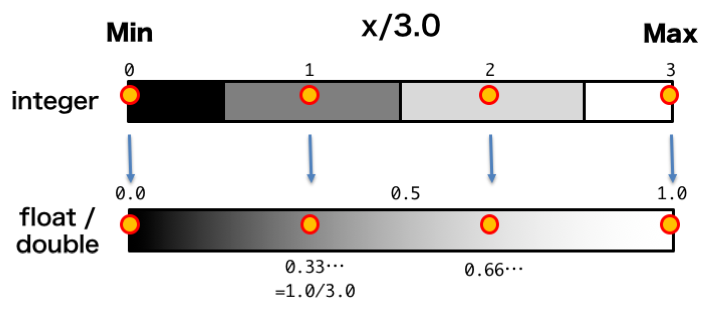
デジタルの値からアナログ相当の 0.0〜1.0 に変換するのは定数でただ割れば良い。
とも言い切れません。。
定数で割るだけ方式
まずは素直な方法。そのままスケールを変えるだけです。
これはこれで正しいのですが、量子化誤差で消えた情報はそのまま忘れて良いのか気になりますよね。
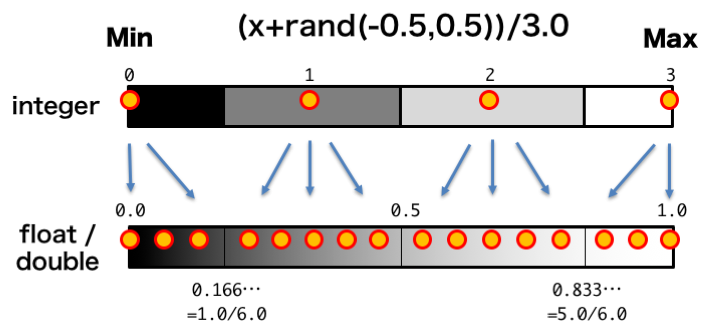
ランダムを入れる方式
[要出典]
もともと、デジタル値は、アナログ量の一定範囲を代表した値です。そこで、いっその事ランダムで戻して元々の範囲を全部使えるようにしよう。という方法もあります。
最後に
ビット深度間の変換は後編にて。
- RGB ビット深度のうんちく (後編) 〜 整数型同士の変換