Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@youce

ドブル (Dobble / Spot it!) 自作 (5): 3枚に1つのシンボルが共通するデッキ

Last updated at Posted at 2024-09-23

はじめに

ボードゲーム ドブル (Dobble / Spot it!) を Python 実装した dobble-maker の解説です。

本記事では、 任意の 3 枚のカードに必ず 1 つのシンボルが共通するデッキの構築 について説明します。

作りたいもの

タイトルの通り「3 枚に 1 つのシンボルが共通するドブル」です。

通常版、および前回版はいずれも「2 枚のカード」を選ぶところは変わらなかったので、変わった遊び方ができそうです。

ブロックデザインで考える ⇒ 失敗

まずは失敗作からです。

t=3, λ=1 の Steiner システム で解いてみる

前回記事でブロックデザインについて学んだので、 $t = 3$ 、 $\lambda = 1$ のブロックデザインを構築すれば良いのかな？と思って調べました。

まず、 $t = 3$ なので、BIBD ではありません（BIBD は $t = 2$ 、$\lambda = 1$ ）。一方で、 $\lambda = 1$ で $t >= 2$ のブロックデザインは、 Steiner system と名前がついており、メジャーなデザインのようです。BIBD を包含するデザインですね。

Steiner システムも t-デザインの一種なので、前回記事の

$$
bk = vr
$$

$$
\lambda \times {}_vC_t = b \times {} _kC_t
$$

を満たします。ここに $\lambda = 1$ を入れると、以下の関係が得られます。

$$
b = \frac{v(v-1)...(v-t+1)}{k(k-1)...(k-t+1)}
$$

$$
r = \frac{(v-1)...(v-t+1)}{(k-1)...(k-t+1)}
$$

$\lambda = 1$ は決まっているので、 $t, k, v$ を与えると $b, r$ が得られます。ここから、Steiner システムは $S(t, k, v)$ デザインと表記されます。 $t \neq 2$ の Steiner システムで対称である制約（ $b=v$ ）が付けられるのかは、未調査です。

Stiner システムの解を得るのは簡単ではないようですが、 Steiner Quadruple Systems1 という特定のパラメータであれば SageMath で求められそうだったので、1 つ解を出してみます（以下は Claude による実装です）。

以下を SageMathCell で実行します。

Steiner(t=3, k=4, v=8)
from sage.combinat.designs.steiner_quadruple_systems import steiner_quadruple_system

# S(3,4,8) Steiner四項系の生成
S_348 = steiner_quadruple_system(8)

print("S(3,4,8) Steinerシステム (Steiner四項系):")
print(S_348)

print("\nブロック (4点集合) の一覧:")
for block in S_348:
    print(block)

print(f"\n点の数: {S_348.num_points()}")
print(f"ブロックの数: {S_348.num_blocks()}")

以下が出力結果です。

Steiner(t=3, k=4, v=8)の解
S(3,4,8) Steinerシステム (Steiner四項系):
Incidence structure with 8 points and 14 blocks

ブロック (4点集合) の一覧:
[0, 1, 2, 3]
[0, 1, 4, 5]
[0, 1, 6, 7]
[0, 2, 4, 6]
[0, 2, 5, 7]
[0, 3, 4, 7]
[0, 3, 5, 6]
[1, 2, 4, 7]
[1, 2, 5, 6]
[1, 3, 4, 6]
[1, 3, 5, 7]
[2, 3, 4, 5]
[2, 3, 6, 7]
[4, 5, 6, 7]

点の数: 8
ブロックの数: 14

結果を確認してみる

先ほどの出力結果は、いつものように、各行がカードで、数値がシンボル ID です。

試しに最初の 3 枚を選択してみます。1 つのシンボルだけが共通していると嬉しいのですが……そうはなっていません。

S(3, 4, 8) の最初の 3 枚
[0, 1, 2, 3]
[0, 1, 4, 5]
[0, 1, 6, 7]

$\lbrace 0, 1 \rbrace$ が共通してしまっています。

ここで思い出すのが、ブロックデザインの $t$ と $\lambda$ の定義です（前回記事参照）。

  • 任意の $t$ 個の要素のセットについて、これらを含むブロックの数（＝ $t$ 個の要素セットの出現回数）は全て等しく $\lambda$ である

改めて先の出力結果を確認します。例えば、任意の $t = 3$ 個の要素のセット $\lbrace 0, 1, 2 \rbrace$ が出現するのは $[0, 1, 2, 3]$ だけで 1 回です。適当に $\lbrace 1, 4, 6 \rbrace$ を選んでも、 $[1, 3, 4, 6]$ の 1 回です。ブロックデザインにおける定義はきちんと満たしているので、何らかのバグ、というわけでもなさそうです。

つまりブロックデザインの $t$ と $\lambda$ は、ドブルのルールと直接対応しない、ということになります。少なくとも $t = 3$ 、 $\lambda = 1$ の Steiner システムでは、本記事の目的は達成できないことがわかりました。

誤り訂正符号の導入

残念ながらブロックデザインでは解けなかったので、別の解法が必要です。

そこで今回は、こちらのスレッドを参考に、誤り訂正符号で解きます。正直、誤り訂正符号がほとんど理解できていないので、直接使わない内容は説明を省略しますが、ご容赦ください。

誤り訂正符号の概要

誤り訂正符号とは、あるベクトルを生成行列 $\boldsymbol{G}$ で変換したあと、エラーでいずれかの値が変化してしまった場合でも、検査行列 $\boldsymbol{H}$ を使うとエラー位置を特定できる、という理論です。

【誤り訂正符号の用語の説明】読まなくてもドブルの話はできるので、飛ばしても大丈夫です。

以下のベクトル・行列演算は、全て任意の有限体（ガロア体）上で計算されます。誤り訂正符号は情報工学でよく使われるため 0 と 1 のみを扱う $GF(2)$ で説明されることが多いですが、 $GF(3)$ 、 $GF(2^2)$ 、 $GF(5)$ など任意の有限体で扱えます。

エンコーディング（符号化）

  • 元データとなる入力ベクトル（メッセージベクトル、情報ベクトル $\boldsymbol{m}$ 、サイズは $k \times 1$ ）を生成行列 $\boldsymbol{G}$ （サイズは $k \times n$ 、 $k < n$ ）で変換して、新たなベクトル（コードワード、符号語 $\boldsymbol{c} = \boldsymbol{G}^T \boldsymbol{m}$ 、サイズは $n \times 1$ ）を生成
  • この処理をエンコーディング（符号化）と呼ぶ
    • コードワード $\boldsymbol{c}$ はメッセージベクトル $\boldsymbol{m}$ に対して $(n-k)$ 次元の冗長性が付与されたことになる

エラー検出

  • コードワード $\boldsymbol{c}$ は地点 A から地点 B に送信され、この際、通信エラーでベクトルのどこかの値が変化してしまったとする。 B で受け取ったベクトルを受信ベクトル $\boldsymbol{r}$ （サイズは $\boldsymbol{c}$ と同じ $n \times 1$ ）とする。
  • 受信ベクトル $r$ に対して検査行列 $\boldsymbol{H}$ （サイズは $(n-k) \times n$ ） を掛けたベクトル（シンドローム $\boldsymbol{s} = \boldsymbol{H} \boldsymbol{r}$ 、 サイズは $(n-k) \times 1$ ）を得る
  • エラーがなければシンドローム $\boldsymbol{s} = \boldsymbol{0}$ となる
    • これは $\boldsymbol{G}$ 、 $\boldsymbol{H}$ が $\boldsymbol{G} \boldsymbol{H}^T =\boldsymbol{0}$ を満たすように設計されているため

エラー訂正

  • エラーが検出されたら、受信ベクトル $\boldsymbol{r}$ のエラーを訂正する
  • 本記事では使わないので、詳細は省略します

デコーディング（復号化）

  • エラー訂正後のベクトルに生成行列 $\boldsymbol{G}$ の逆行列を掛けて（あるいはそれに相当する専用アルゴリズムによって）元のメッセージベクトルを算出する
  • 本記事では使わないので、詳細は省略します

検査行列 H の特性

本記事で大事なのは、検査行列 $\boldsymbol{H}$ です。検査行列 $\boldsymbol{H}$ には、次の特徴があります。

  • 生成行列 $\boldsymbol{G}$ 及び検査行列 $\boldsymbol{H}$ の性能を表す指標として、最小距離 $d$ がある
  • 最小距離 $d$ で設計された $\boldsymbol{H}$ の任意の $(d-1)$ 本の列ベクトルは、線形独立である
  • $\boldsymbol{H}$ の $(d-1)$ 本の列ベクトルが張る部分空間について、直交補空間の次元は 1 である

検査行列 H を使ったデッキ構築

ここから、検査行列 $\boldsymbol{H}$ を使ったドブルデッキの構築手順の解説です。ポイントは、検査行列の特性である「任意の $(d-1)$ 本の列ベクトルは線形独立」になることです。

  • 検査行列から任意に $(d-1)$ 本の列ベクトルを取得し、そのインデックスを「カード ID」と解釈する
  • $(d-1)$ 本の列ベクトルが張る部分空間の直交補空間は 1 次元であり、その基底ベクトルが 1 本得られる
    • これらは所定の有限体上で計算されることに注意
  • 上記の直交補空間の基底ベクトルをシンボルと解釈する。すなわち「$(d-1)$ 本の列ベクトルの組に現れる 1 本の列ベクトル」を、「$(d-1)$枚のカードの組に現れる 1 個の共通シンボル」と解釈する
  • 上記の $(d-1)$ 本の選択を $_n C _{d-1}$ 回繰り返して、各カードが持つシンボルを記憶する

それでは、以下で各処理の詳細を説明します。ここでは、本記事の目的である「 $\tau = 3$ 枚のカードに 1 個のシンボルが共通する」デッキを構築していきます。

条件を満たす検査行列 H を生成

条件の確認

誤り訂正符号のパラメータは、 $[n, k, d]_q$ で表現されます。今回、「 $\tau = 3$ 枚のカードに 1 個のシンボルが共通する」デッキを構築するために、$[n, k=n-d, d = \tau + 1]_q = [n, n-4, 4]_q$ で構成される誤り訂正符号の検査行列を利用します2。

$n$は任意の自然数、$q$は任意の有限体の位数（つまり素数の累乗）です。

CodeTables.de で検索

任意のパラメータに対応する誤り訂正符号の生成行列 $\boldsymbol{G}$ と検査行列 $\boldsymbol{H}$ は、 CodeTables.de の Linear Codes のコンテンツから検索することができます。

上記のサイトは $n$ 、 $k$ 、 $q$ から登録されている誤り訂正符号のパラメータを検索する構成です。ただし今回は $d=4$ だけ決まっていて他は何でも良いので、 $q$ だけ指定して一覧を表示してみます。

Complete tables with ... over GF(q) の下のボタンから GF(2) を押してみます。

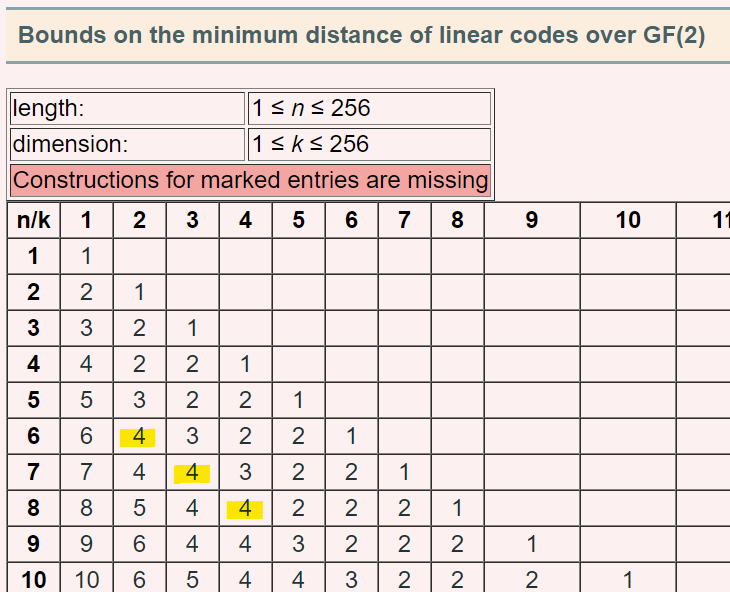
すると、行に $n$ 、 列に $k$ 、セルの値が $d$ のテーブルが表示されます。今探しているのは $n$ は任意、 $k = n-4$ 、 $d = 4$ なので、それを満たすいずれかのセルをクリックします。

例えば $[n, k, d] = [6, 2, 4]$ のセルをクリックしてみるとこちらが表示されます。

これ、作り方が全く分からないと思うのですが、実は MAGMA という数値計算ソフトを使って生成する手順が書いてあります。

MAGMA で実装

MAGMA は Magma Calculator で実行できます。MAGMA 用のスクリプトを書かないといけないのですが、ChatGPT や Claude に訊きつつ、関数はよく間違えるので MAGMA の document で検索しながら実装します。

以下が $[6, 2, 4]_{q=2}$ の生成行列 $\boldsymbol{G}$ と検査行列 $\boldsymbol{H}$ を生成する MAGMA スクリプトとその実行結果です。

[6,4,2] over GF(2)
// Cordaro-Wagner code of length 6 を生成 (Cordaro-Wagner codeのfieldは2固定)
C := CordaroWagnerCode(6);

// 生成行列, 検査行列を生成
G := GeneratorMatrix(C);
H := ParityCheckMatrix(C);

print "Generator Matrix:", G;
print "Parity-Check Matrix:", H;
実行結果
Generator Matrix:
[1 1 0 0 1 1]
[0 0 1 1 1 1]
Parity-Check Matrix:
[1 0 0 1 0 1]
[0 1 0 1 0 1]
[0 0 1 1 0 0]
[0 0 0 0 1 1]

パラメータ毎に MAGMA スクリプトは作り直す必要がありますが、使う関数は CodeTables.de にそのまま書かれているので、容易に実装できるかと思います。

これで検査行列 $\boldsymbol{H}$ が作れるようになりました。

検査行列 H から τ 本の列ベクトルを選択

先ほどの例で $[n, k, d]_q = [n, k=n-d, d = \tau + 1]_q = [6, 2, 4]_2$ の検査行列 $\boldsymbol{H}$ が得られました。以降の説明のため、$\boldsymbol{H}$の各列ベクトルを$\boldsymbol{h}_i$としておきます。

\boldsymbol{H} = \begin{pmatrix}
1 & 0 & 0 & 1 & 0 & 1 \\
0 & 1 & 0 & 1 & 0 & 1 \\
0 & 0 & 1 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 1 \\
\end{pmatrix}
= \begin{pmatrix}\boldsymbol{h}_1 & \boldsymbol{h}_2 & \boldsymbol{h}_3 & \boldsymbol{h}_4 & \boldsymbol{h}_5 & \boldsymbol{h}_6 \end{pmatrix}

さて、先に説明した検査行列の特性によれば、この中の $(d-1) = \tau$ 本の列ベクトルは、必ず線形独立になります。そこで、ここでは $\lbrace \boldsymbol{h}_1,\boldsymbol{h}_3,\boldsymbol{h}_6 \rbrace$ を選ぶとします。

\boldsymbol{h}_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix},
\boldsymbol{h}_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix},
\boldsymbol{h}_6 = \begin{pmatrix} 1 \\ 1 \\ 0 \\ 1 \end{pmatrix}

直交補空間の基底ベクトルを算出

先ほど選んだ $\tau=3$ 本の列ベクトルは、線形独立の関係にあります。つまり 3 次元部分空間の基底ベクトルとなります。そして列ベクトルの次元は $(n-k)=4$ 次元ですから、3 次元部分空間の直交補空間の次元は $4-3=1$ 次元となります。

そこで、この直交補空間の基底ベクトルを求めます。以下がその Python 実装です。

直交補空間の算出
import galois
import numpy as np

gf = galois.GF(2)
H = gf([
    [1, 0, 0, 1, 0, 1],
    [0, 1, 0, 1, 0, 1],
    [0, 0, 1, 1, 0, 0],
    [0, 0, 0, 0, 1, 1],
])  # 有限体上で検査行列を定義

h_selected = H[:, [0, 2, 5]]  # Hから列ベクトルを3本選択
vecs_orth = selected.left_null_space()  # 列ベクトルが張る部分空間の補空間を算出
assert len(vecs_orth) == 1

vec_orth = vecs_orth[0]

print(vec_orth)

以上により、直交補空間の基底ベクトルが得られました3。

列ベクトルをカード、補空間の基底ベクトルを共通シンボルとみなして記憶

続いて、先ほど選んだ $\tau$ 本の列ベクトルをそれぞれカードとみなし、上記の基底ベクトルを共通シンボルとみなして、関係を記憶します。

まず、選択済みの $\tau$ 本の列ベクトルのインデックスを取得します。ここでは $\lbrace 1, 3, 6 \rbrace$ です。

次に、直交補空間の基底ベクトル $\boldsymbol{v}_ {orth}$ をシンボル ID 化します。具体的には、 $\boldsymbol{v}_ {orth}$ を $(n-k)$ 桁の $q$ 進数と見なして変換します。例えばここまでに得られた $\boldsymbol{v}_ {orth} = \begin{pmatrix} 0 & 1 & 0 & 1 \end{pmatrix}^T$ ですから、これを $(0101)_{q=2} = 5$ とします。

最後に、列ベクトルのインデックスと直交補空間の基底ベクトルを変換したシンボル ID を紐づけます。すなわち「カード 1、カード 3、カード 6 が、シンボル 5 を有する」として記憶します。

全組み合わせを記憶してデッキを出力

上記の列ベクトルの選択を、全 ${} _n C _{\tau}$ パターンで繰り返します。

回数 選択列 $\boldsymbol{v}_{orth}^T$ カード 1 2 3 4 5 6
1 1, 3, 6 (0 1 0 1) 5 5 5
2 1, 2, 3 (0 0 0 1) 1, 5 1 1, 5 5
3 1, 2, 4 (0 0 0 1) 1, 5 1 1, 5 1 5
4 1, 2, 5 (0 0 1 0) 1, 2, 5 1, 2 1, 5 1 2 5
... ... ... ... ... ... ... ... ...

構築されたデッキの特性

上記の手順で「3 枚に 1 つのシンボルが共通するデッキ」を構築することができました。

カードあたりのシンボル数や、総カード枚数を変更したい場合、 CodeTables.de から条件を満たす検査行列を検索し、その都度 MAGMA で実装していく必要があります。

また、ここで構築したデッキは、これまで構築してきたデッキと違って、バランスが整っていません。

  • 各シンボルの出現回数は均一ではない
  • カードあたりのシンボル数は均一ではない
    • おおむね揃いますが、±1 ～ 2 程度は差が生じます
  • 検査行列のパラメータから出現するシンボル数が予想できない
    • $\boldsymbol{v}_{orth}$の次元と有限体の位数から最大数は予想できますが、実際にそれらがすべて出現するかは未確認です

などです。ですがゲームとして遊ぶ分にはこれらはそこまでの欠点ではなく、2 枚に 1 つの共通シンボルとは違って難易度が非常に高いので、その点では満足できる構成になりました。

最後に

今回の作り方では、誤り訂正符号における $d = \tau + 1$ の値を変えた検査行列を作ってあげれば $τ$ 枚に 1 つの共通シンボルを持つデッキは様々なバリエーションで作れそうです（必要なシンボル数が膨大になってしまいそうではありますが……）。

参考

  • Dobble Algorithm for three or more matches.
    • 今回はこちらの Mike Earnest 氏の回答を実装したものになります
  • CodeTables.de
    • 誤り訂正符号における生成行列の算出方法をまとめた膨大なデータベースです
    • MAGMA の存在を全く知らなかったので、ここの理解は非常に苦労しました

  1. $S(3,4,v)$ デザイン、かつ $v$ を 6 で割った余りが 2 または 4 である（ $v \equiv 2 \ or \ 4 \ (mod \ 6)$ ）ことが条件のデザインで、 $SQS(v)$ と表記される、そうです。 ↩

  2. ここでは $d=n-k$ でありコードワード $\boldsymbol{c}$ の冗長性 $(n-k)$ と最小距離 $d$ が一致していますが、一般に冗長性と最小距離が必ず一致する、ということではないようです。 ↩

  3. 補空間は一次元であり有限体では正負がないため、正規化（モニック化）すれば基底ベクトルは一意に定まります。そのため vec_orth はモニック化するべき（でないとこのあとの処理でシンボル数が過剰に増えてしまう）です。ただ、明示的にしなくても既に left_null_space() でされていたので、ここでは割愛しました。 ↩

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?