しっかり学ぶシェーダプログラミング【グーローシェーダ編】

はじめに

こんにちは、個人ゲーム開発で忙しい@yoship1639です。
しばらく時間が空いてしまい申し訳ございません。

前回、シェーダをさわる前に編で、簡単にシェーダの説明と書く前に持つべき知識の説明をしました。
ご覧になってない方は軽く目を通していただけたら幸いです。

今回は、シェーダの最も基本ともいえるグーローシェーダについて説明、0から実装していきたいと思います。

##目次

1. しっかり学ぶシェーダプログラミング【シェーダをさわる前に編】
2. しっかり学ぶシェーダプログラミング【グーローシェーダ編】<-本記事

グーローシェーダの概要

グーローシェーディング（英: Gouraud shading）は、物体の表面での光と色の変化をシミュレートするコンピュータグラフィックスの手法の1つ。アンリ・グーロー (Henri Gouraud) が考案し1971年に公表した。実際には、粗いポリゴン表面に滑らかな照明効果を施すのに使われ、各ピクセルの計算にそれほど時間がかからない。
※wikipediaから引用

グーローシェーダは、モデルの陰影を比較的軽量にシミュレートする時に使われる、昔から存在する基本的なシェーダです。
モデルの色付けをする基本中の基本のシェーダであると覚えておいてください。

最近のシェーダは基本的にピクセルシェーダ(GLSLは本来フラグメントシェーダと呼びますが、今回はピクセルシェーダで統一します)でライティング処理を行うのですが、このシェーダは頂点シェーダでライティング処理を行うことで、ライティングによる負荷を低減しています。

グーローシェーダはゲームで言うと大体、初代プレイステーションや、ニンテンドー64の時代に使われているシェーダです。
この時代は、自分で自由にシェーダが書けなくて、グーローやフォンが強制されています。
しかし、フォンはグーローよりも高負荷なため、基本はグーローを使っていたと思われます。

FF7の画像を見てみると、ポリゴンモデル3体以外はただのスプライト(絵)です。
スプライトやビルボードの表示はとても軽いので3Dの代わりに利用されることが多いです。
ただの１枚絵で周囲の雰囲気を良く表現できるならその方が良いから、スプライトで表現しているんですね。

軽量化のため、この頃のゲームはマテリアルのDiffuseとディレクショナルライト1つのみで構成されていることが多いです。

それでは、実際にグーローシェーダのアルゴリズムを見てみたいと思います。

基本的なグーローシェーダを実装する

グーローシェーダのアルゴリズムは以下の通りです。

###頂点シェーダ

1. MVP行列とM逆転置行列とモデルの頂点データと法線データとマテリアルデータ、ディレクショナルライトのデータを受け取る
2. 頂点のMVP変換を行う
3. 法線のM変換を行う
4. 法線とディレクショナルライトの角度を求める(内積)
5. マテリアルのdiffuseと内積を掛け、色を算出する
6. 色をピクセルシェーダに渡す

###ピクセルシェーダ

1. 色データを頂点シェーダから受け取る
2. 頂色をそのまま出力する

色の計算を頂点シェーダが行っています。

GLSLコードに表すとこうなります。(glslのバージョンは4.2を使います)
・頂点シェーダ

gouraud.vert

#version 420

uniform mat4 MVP; // mvp行列
uniform mat4 MIT; // m逆転置行列 (Model Inverse Transposeの略)
uniform vec4 diffuse = vec4(1.0); // マテリアルのdiffuseカラー
uniform vec3 wLightDir; // ワールド座標のディレクショナルライトの向き

layout (location = 0) in vec3 position; // 頂点データ
layout (location = 1) in vec3 normal; // 法線データ

layout (location = 0) out vec4 Color; // ピクセルシェーダに渡す色

void main()
{
    gl_Position = MVP * vec4(position, 1.0); // 頂点のmvp変換
    vec3 n = normalize(mat3(MIT) * normal); // 法線のm変換
    float nl = clamp(dot(n, normalize(-wLightDir)), 0.0, 1.0); // 法線とライトの内積を算出
    vec3 c = diffuse.rgb * nl; // 最終色を算出
    c = clamp(c, 0.0, 1.0); // 0.0 ~ 1.0に色を収める
    Color = vec4(c, diffuse.a);
}

・ピクセルシェーダ

gouraud.flag

#version 420

layout (location = 0) in vec4 color;

layout( location = 0 ) out vec4 FragColor;
 
void main()
{
    FragColor = color;
}

これが、グーローシェーダの基本の処理手順です。
ひとつづつ解説します。

頂点シェーダ

1. MVP行列とM逆転置行列とモデルの頂点データと法線データとマテリアルデータ、ディレクショナルライトのデータを受け取る

uniform mat4 MVP; // mvp行列
uniform mat4 MIT; // m逆転置行列 (Model Inverse Transposeの略)
uniform vec4 diffuse = vec4(1.0); // マテリアルのdiffuseカラー
uniform vec3 wLightDir; // ワールド座標のディレクショナルライトの向き

layout (location = 0) in vec3 position; // 頂点データ
layout (location = 1) in vec3 normal; // 法線データ

まず、頂点シェーダではシェーダに必要なデータを受け取ります。
(厳密には、CPUからGPUへ予めデータをVRAMへ移し、シェーダプログラムを実行する時にVRAMから必要なデータを参照しシェーダが走ります。)
MVP行列、M逆転置行列、モデルの頂点データ、法線データ、マテリアルデータ、ディレクショナルライトはすべてグーローシェーダに必要なデータなので受け取ります。それ以外のデータは現時点では使わないのでいりません。
個々の用語の解説はしないので、各自調べていただければ幸いです。
ディレクショナルライトはワールド座標のライトを受け取っておきます。(他に、ビュー座標のライトもありますが今回はワールド座標を使います)

2. 頂点のMVP変換を行う

gl_Position = MVP * vec4(position, 1.0); // 頂点のmvp変換

最初に行う処理は、頂点データのMVP変換です。
MVP変換を行うと、ローカル座標の頂点が、ローカル->ワールド->ビュー->プロジェクションと一気に変換されます。
なぜ行うかというと、ピクセルシェーダにMVP変換を施した頂点データを渡さなくちゃピクセルシェーダが動かないからです。
この処理は、グーローシェーダに限らずあらゆるモデルシェーダで行われる処理なので、定型として覚えておきましょう。

3. 法線のM変換を行う

vec3 n = normalize(mat3(MIT) * normal); // 法線のm変換

次に、法線データのM変換を行います。つまりローカル法線->ワールド法線に変換します。
ワールド法線に変換する理由は、ディレクショナルライトと同じ座標系で計算をしたいからです。
そのため、ディレクショナルライトはワールド座標として受け取っておきます。

コードを見るといろいろ気になる点があります。
まず、mat3(MIT)です。これはMITは4x4行列なのですが、掛け合わせたいnormalは3要素しかないので次元が合いません。そのため、3x3に変換させ、次元を合わせています。

一番の疑問は、なぜM行列ではなくMIT行列を使うのかです。
これには理由があって、法線は方向であり位置ではありません。
そして、方向の座標系を変換させるには逆転置行列を使わなくてはいけないのです。
細かい理由は調べていただければ出てきます。実際にM行列で計算すると、法線がおかしなことになります。

最後にnormalizeを施して正規化させます。
正規化とは、ベクトルの長さを1にすることです。
方向を表すベクトルは基本的にnormalizeを適宜施し正規化された状態にしてやる必要があります。
そうしないと、計算結果がどんどんずれてしまうからです。

4. 法線とディレクショナルライトの角度を求める(内積)

float nl = clamp(dot(n, normalize(-wLightDir)), 0.0, 1.0); // 法線とライトの内積を算出

次に、先ほど求めた法線とディレクショナルライトの角度を求めます。実際に求めるのはΘではなく内積です。
なぜ内積を使うのかというと、実際の計算に使うのに都合が良く更に高速だからです。

*dot(n, normalize(-wLightDir))*は、法線と正規化させたディレクショナルライトの向きの内積を取る処理です。
wLightDirがマイナスなのは法線と逆向きの状態を直すためです。
dotの結果は、向きが近ければ近いほど1.0に近づき、向きが反対に近いほど-1.0に近づきます。
正規化されたベクトル同士の内積は必ず-1.0 ~ 1.0の間に収束されます。
1.0に近いと明るく、0.0に近いと暗くなります。

求めた内積はclampを施し、0.0 ~ 1.0にクリップします。
マイナス部分は光の量を逆に奪ってしまうので、マイナスにならない様にします。

5. マテリアルのdiffuseと内積を掛け、色を算出する

vec3 c = diffuse.rgb * nl; // 最終色を算出

次に、diffuseと先ほど求めた内積を掛け合わせ、出力したい色を求めます。
これで、ディレクショナルライトの向きに近いほど明るく、反対であるほど暗い色なります。

6. 色をピクセルシェーダに渡す

layout (location = 0) out vec4 Color; // ピクセルシェーダに渡す色

void main()
{
    ...
    c = clamp(c, 0.0, 1.0); // 0.0 ~ 1.0に色を収める
    Color = vec4(c, diffuse.a);
}

最後に、色を出力します。ピクセルシェーダに渡すという意味です。
色を出力する前に0.0 ~ 1.0の間に色を収めています。
もし、この範囲を外れることになった場合、シェーダの色の出力がおかしくなってしまうからです。
アルファ成分に関しては、diffuseのアルファ成分をそのまま使います。
もし、先ほどの処理の結果をアルファにも適用してしまうと、当然、透明になってしまいます。

頂点データも色も出力できたので、ピクセルシェーダに移ります。

ピクセルシェーダ

1. 色データを頂点シェーダから受け取る

layout (location = 0) in vec4 color;

頂点シェーダから渡されたデータを受け取ります。
説明は不要ですね。

2. 頂色をそのまま出力する

layout( location = 0 ) out vec4 FragColor;
 
void main()
{
    FragColor = color;
}

頂点シェーダの色をそのままピクセルシェーダの出力色にします。
ピクセルシェーダでやることはグーローシェーダでは特にありません。

基本のグーローシェーダの見た目

球

アリシア・ソリッド

基本的なグーローシェーダは実装できましたが、スペキュラハイライトとテクスチャが付いてません。
なので、テクスチャとスペキュラを追加したいと思います。

#テクスチャ+スペキュラ付きのグーローシェーダを実装する

テクスチャとスペキュラを追加した頂点シェーダはこうなります。追加項目にコメントを割り振っています。

gouraud.vert

#version 420

uniform mat4 M; // M行列
uniform mat4 MVP;
uniform mat4 MIT;
uniform vec4 diffuse = vec4(1.0);
uniform vec4 specular = vec4(1.0); // specularカラー
uniform float shininess = 10.0; // スペキュラ係数
uniform vec3 wLightDir;
uniform vec3 wCameraPos; // ワールド座標のカメラの位置

// スペキュラを取得
// IN: surfToEye 頂点から視点への向き
// IN: normal 法線
// IN: surfToLight 頂点からライトへの向き
// IN: shininess スペキュラ係数
// OUT: スペキュラ
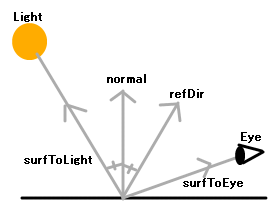
float calcSpecular(vec3 surfToEye, vec3 normal, vec3 surfToLight, float shininess)
{
	vec3 refDir = normalize(reflect(-surfToLight, normal));
	float factor = dot(surfToEye, refDir);
	return pow(max(factor, 0), shininess);
}


layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
layout (location = 2) in vec2 uv; // UVデータ

layout (location = 0) out vec4 Color;
layout (location = 1) out vec2 UV;

void main()
{
    gl_Position = MVP * vec4(position, 1.0);
    vec3 n = normalize(mat3(MIT) * normal);
    float nl = clamp(dot(n, normalize(-wLightDir)), 0.0, 1.0);
    vec3 c = diffuse.rgb * nl;

    // スペキュラ処理
    vec4 wPos = M * vec4(position, 1.0); // ワールド座標の頂点位置を算出
    vec3 surfToEye = normalize(wCameraPos - wPos); // 頂点から視点の向きを算出
    vec3 surfToLight = normalize(-wLightDir); // 頂点からライトの向きを算出
    float spec = calcSpecular(surfToEye, n, surfToLight, shininess); // スペキュラ計算
    c.rgb += vec3(spec); // スペキュラを適用

    c = clamp(c, 0.0, 1.0);
    Color = vec4(c, diffuse.a);
    UV = uv; // UVはそのままピクセルシェーダに渡す
}

まず、スペキュラ処理をする頂点シェーダから見ていきます。

頂点シェーダ

入力データの追加

uniform mat4 M; // M行列
uniform vec4 specular = vec4(1.0); // specularカラー
uniform float shininess = 10.0; // スペキュラ係数
uniform vec3 wCameraPos; // ワールド座標のカメラの位置

layout (location = 2) in vec2 uv; // UVデータ

新たに、M行列、スペキュラ、スペキュラ係数、カメラ位置を定義し、入力データにUVが増えました。
M行列、スペキュラ、スペキュラ係数、カメラ位置はスペキュラ計算に必要で、UVはテクスチャに必要です。

スペキュラ関数の定義

// スペキュラを取得
// IN: surfToEye 頂点から視点への向き
// IN: normal 法線
// IN: surfToLight 頂点からライトへの向き
// IN: shininess スペキュラ係数
// OUT: スペキュラ
float calcSpecular(vec3 surfToEye, vec3 normal, vec3 surfToLight, float shininess)
{
	vec3 refDir = normalize(reflect(-surfToLight, normal));
	float factor = dot(surfToEye, refDir);
	return pow(max(factor, 0), shininess);
}

新たに、スペキュラを計算するために関数を定義しました。

vec3 refDir = normalize(reflect(-surfToLight, normal));

まず、ライトベクトル(-surfToLight)と法線ベクトル(normal)から反射ベクトル(refDir)を求めます。

float factor = dot(surfToEye, refDir);

次に、反射ベクトル(refDir)と視点ベクトル(surfToEye)からスペキュラハイライトの値を求めます。

return pow(max(factor, 0), shininess);

最後に、スペキュラの強さを指数で変えます。
shininessが小さければ小さいほど、スペキュラは大きくなります。

この処理は普遍的に使えるので、関数にしています。

スペキュラ処理

vec4 wPos = M * vec4(position, 1.0); // ワールド座標の頂点位置を算出
vec3 surfToEye = normalize(wCameraPos - wPos); // 頂点から視点の向きを算出
vec3 surfToLight = normalize(-wLightDir); // 頂点からライトの向きを算出
float spec = calcSpecular(surfToEye, n, surfToLight, shininess); // スペキュラ計算
c.rgb += vec3(spec); // スペキュラを適用

これらは、先ほどの関数を利用するための下準備となっています。
気を付ける点は、*vec4 wPos = M * vec4(position, 1.0);*ですね。
これは、他のライトやカメラと同じ座標系にするためにローカル頂点データをワールド座標に直しています。
最後にスペキュラを色に加算しています。乗算ではだめです。おかしなことになります。

また、頂点からライトの向きは*normalize(-wLightDir)*で問題ありません。
なぜなら、normalize(wPos - wLightPos)だった場合、wLightPosは無限遠なので、結局-wLightDirに落ち着くからです。

頂点シェーダでスペキュラの適用が出来たので、次はピクセルシェーダに移ります。

ピクセルシェーダ

gouraud.flag

#version 420

layout (binding = 0) uniform sampler2D diffuseMap; // diffuseマップ

layout (location = 0) in vec4 color;
layout (location = 1) in vec2 uv; // UVデータ

layout( location = 0 ) out vec4 FragColor;
 
void main()
{
    vec4 diff = texture(diffuseMap, uv); // テクスチャを参照
    FragColor = color * diff; // 頂点シェーダから渡った色にテクスチャの色を掛け出力
}

特に目立った処理もなく、コメントで説明しているので、詳細な解説は割愛します。

テクスチャ+スペキュラ付きのグーローシェーダの見た目

アリシア・ソリッド (shininess = 4.0)

アリシア・ソリッド (shininess = 10.0)

shininessが大きいほどスペキュラが小さくなっているのが分かります。

しかし、あまり見た目は良くありません。
これは法線とライトベクトルの内積の値で光の強さを決めてしまっているからです。(ランバートといいます)
これをハーフランバートと呼ばれる計算方法に変えます。

float nl = clamp(dot(n, normalize(-wLightDir)), 0.0, 1.0);
nl = nl * 0.5 + 0.5;

これだけでOKです。これで、0.0 ~ 1.0 の光の強さが 0.5 ~ 1.0 に圧縮されます。
これでレンダリングすると、

かわいいアリシアちゃんになりました。

グーローシェーダコード全文

頂点シェーダ

gouraud.vert

#version 420

uniform mat4 M;
uniform mat4 MVP;
uniform mat4 MIT;
uniform vec4 diffuse = vec4(1.0);
uniform vec4 specular = vec4(1.0);
uniform float shininess = 10.0;
uniform vec3 wLightDir;
uniform vec3 wCameraPos;

// スペキュラを取得
// IN: surfToEye 頂点から視点への向き
// IN: normal 法線
// IN: surfToLight 頂点からライトへの向き
// IN: shininess スペキュラ係数
// OUT: スペキュラ
float calcSpecular(vec3 surfToEye, vec3 normal, vec3 surfToLight, float shininess)
{
	vec3 refDir = normalize(reflect(-surfToLight, normal));
	float factor = dot(surfToEye, refDir);
	return pow(max(factor, 0), shininess);
}


layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
layout (location = 2) in vec2 uv;

layout (location = 0) out vec4 Color;
layout (location = 1) out vec2 UV;

void main()
{
    gl_Position = MVP * vec4(position, 1.0);
    vec3 n = normalize(mat3(MIT) * normal);
    float nl = clamp(dot(n, normalize(-wLightDir)), 0.0, 1.0);
    nl = nl * 0.5 + 0.5;
    vec3 c = diffuse.rgb * nl;

    // スペキュラ処理
    vec4 wPos = M * vec4(position, 1.0);
    vec3 surfToEye = normalize(wCameraPos - wPos);
    vec3 surfToLight = normalize(-wLightDir);
    float spec = calcSpecular(surfToEye, n, surfToLight, shininess);
    c.rgb += vec3(spec);

    c = clamp(c, 0.0, 1.0);
    Color = vec4(c, diffuse.a);
    UV = uv;
}

ピクセルシェーダ

gouraud.flag

#version 420

layout (binding = 0) uniform sampler2D diffuseMap; // diffuseマップ

layout (location = 0) in vec4 color;
layout (location = 1) in vec2 uv; // UVデータ

layout( location = 0 ) out vec4 FragColor;
 
void main()
{
    vec4 diff = texture(diffuseMap, uv); // テクスチャを参照
    FragColor = color * diff; // 頂点シェーダから渡った色にテクスチャの色を掛け出力
}

まとめ

シェーダの基本中の基本のグーローシェーダを実際に書いて実装してみました。
これができないと、フォンシェーダや法線マップ、物理ベースシェーダなど出来ないと思うので、しっかりおさえていただければ幸いです。

みんなもシェーダ頑張ろう！