表面符号の論理ビット操作

Posted at 2025-12-02

これはトポロジカル符号の実装実験の記事です。

前回は [5,1,3] 平面符号のエンコードとシンドローム測定を行いました。
今回はエンコードした論理ビットに対して、ゲート操作を行います。

Z, X ゲート

論理 Z ゲート：$q_0, q_1$ に Z ゲートを作用させる。
論理 X ゲート：$q_0, q_3$ に X ゲートを作用させる。

これらは実験するまでもなく、符号語を見れば明らかでしょう。

H ゲート

H ゲートはすべてのデータビットに対して H ゲートを作用させます。変数 sc は前回のものを使用します。

q = QuantumRegister(9)
c = ClassicalRegister(5)
circ = QuantumCircuit(q, c)

circ.append(sc.copy(), q)

for i in range(5):
    circ.h(i)

circ.measure(q[:5], c)

result = backend_sim.run(transpile(circ.decompose()), shots=n_shots).result()
counts = result.get_counts(0)
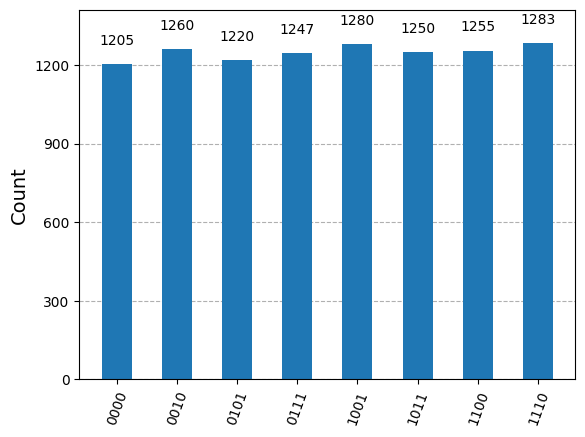
plot_histogram(counts)

結果は
$$
\ket{\psi} = \frac{1}{2\sqrt{2}} (\ket{00000} + \ket{11000} + \ket{10110} + \ket{01110} + \ket{10101} + \ket{01101} + \ket{00011} + \ket{11011})
$$
になっています。これは新たな符号語
$$
\ket{0_L}' = \frac{1}{2} (\ket{00000} + \ket{10110} + \ket{11011} + \ket{01101})
$$
$$
\ket{1_L}' = \frac{1}{2} (\ket{00011} + \ket{10101} + \ket{11000} + \ket{01110})
$$
を定義して表記すれば、
$$
\ket{\psi} = \frac{1}{\sqrt{2}} (\ket{0_L}' + \ket{1_L}') = H\ket{0_L}'
$$
になるから、論理 H ゲートが実現できたことになります。
厄介なのは、単に H ゲートを作用させたいだけにもかかわらず、符号語が変わってしまったことです。

今回の場合は、この新しい符号をよく見ると図のように、
元の符号の Z スタビライザーと X スタビライザーを交換したものになっています。
（H ゲートは X 基底と Z 基底を変換する演算だから当たり前ですが…）
$q_0 \rightarrow q_1, q_1 \rightarrow q_4, q_4 \rightarrow q_3, q_3 \rightarrow q_0$ と置き換えたものと見ることもできるので、簡単に元の符号語に戻すことができます。

CNOT ゲート

論理ビットを 2 個用意して、対応するすべてのデータビットについて CNOT ゲート操作を行うことで論理 CNOT 操作ができます。

実験では $\ket{0_L}$ に論理 H ゲートを作用させて、$\frac{1}{\sqrt{2}} (\ket{0_L}' + \ket{1_L}')$ としてから量子ビットの順序を入れ替えて
$\frac{1}{\sqrt{2}} (\ket{0_L} + \ket{1_L})$ とした状態をコントロールビットとします。

2 個の論理ビットを使用するので、全体で 18 量子ビットの回路になります。
18 量子ビット程度であれば普通の PC でシミュレートできると思っていましたが、
古典ビットを 10 個用意して観測しようとするとメモリ不足エラーが発生してしまいました。

古典ビット数を 4 個にすれば動作するので、4 ビットの観測で頑張ってみました。

q = QuantumRegister(18)
c = ClassicalRegister(4)
circ = QuantumCircuit(q, c)

circ.append(sc.copy(), q[0:9])
circ.append(sc.copy(), q[9:])

# １個めの論理ビットに論理 H を作用
for i in range(5):
    circ.h(i)

# 論理 CNOT
circ.cx(0, 10)
circ.cx(1, 13)
circ.cx(2, 11)
circ.cx(3, 9)
circ.cx(4, 12)

circ.measure(q[9:13], c)

result = backend_sim.run(transpile(circ.decompose()), shots=n_shots).result()
counts = result.get_counts(0)
plot_histogram(counts)

ターゲットビットのうち 4 個を観測しました。
この結果から観測結果が $\frac{1}{\sqrt{2}} (\ket{0_L} + \ket{1_L})$ になっていることが推測できると思います。

しかし、この実装では 2 個の論理ビットについて各データビットが結合している必要があります。
特に、超伝導方式の量子コンピュータでは隣り合った量子ビット同士しか結合していないため、実機での実装が難しくなります。そこで、格子手術 (Lattice Surgery) という操作が考え出されました。これについては次回に実験を行います。

T ゲート

誤り耐性のある T ゲート演算を行うためには、Nielsen and Chuang 本[1]の 10.6.2 節で論じられているように、量子テレポーテーションを使った操作を行います。

ここでは簡単のため以下の手順でエンコードします。（[2]参照）

エンコードしたい状態を用意する。（$q_0$ のビットを反転してから T ゲートを作用）
縦一直線に並んだ量子ビット (ここでは $q_0$ と $q_3$) で bell 状態を作る。
通常と同じ手順でエンコードする。

T ゲート操作でノイズが発生してしまえば、エンコード時の CNOT ゲートによって、ノイズが論理ビット全体に伝播してしまうために、この実装には誤り耐性がありません。

circ = QuantumCircuit(9)

# q0 を観測したい状態で初期化し、q3 と bell 状態を作る
circ.x(0)
circ.t(0)
circ.cx(0, 3)

circ.cx(2, 6)
circ.cx(0, 6)
circ.cx(3, 6)

circ.cx(2, 7)
circ.cx(1, 7)
circ.cx(4, 7)

circ.h(5)
circ.cx(5, 0)
circ.cx(5, 1)
circ.cx(5, 2)
circ.h(5)

circ.h(8)
circ.cx(8, 2)
circ.cx(8, 3)
circ.cx(8, 4)
circ.h(8)

circ.reset(5)
circ.reset(6)
circ.reset(7)
circ.reset(8)

circ.save_statevector()

result = backend_sim.run(transpile(circ)).result()

sv = np.array(result.get_statevector())
states = sv.nonzero()[0]

print(sv[states])
for b in states:
    print(format(b, "09b"))

[-2.16489014e-17-2.16489014e-17j -2.16489014e-17-2.16489014e-17j 3.53553391e-01+3.53553391e-01j 3.53553391e-01+3.53553391e-01j 3.53553391e-01+3.53553391e-01j 3.53553391e-01+3.53553391e-01j -2.16489014e-17-2.16489014e-17j -2.16489014e-17-2.16489014e-17j]
000000000
000000111
000001001
000001110
000010010
000010101
000011011
000011100

位相を確認するために、ステートベクトルを参照して整理すると
$$
(0.354 + 0.354 i) (\ket{10010} + \ket{01001} + \ket{01110} + \ket{10101})
= e^{\frac{\pi}{4} i} \ket{1_L}
$$
になり、確かに T ゲートで位相シフトした状態をエンコードできています。

表面符号の論理ビット操作

Z, X ゲート

H ゲート

CNOT ゲート

T ゲート

関連文献