[初心者]文章間の類似度を測る!

概要

ハッカソンで文章間の類似度を基に内容検索が出来るメモ帳を開発しました。
そもそもどうやって文章間の類似度を測定するのか、類似度が分かると何が嬉しいのかなど、自分が分かる範囲で書いていきます。初学者なので、間違っている箇所などあると思いますが、その際は 優しく 教えてください。

類似度が分かると何が嬉しいのか

まずは、文章間の類似度が分かると何がうれしいのか、私の考えを書いておきます。

１，直感的な検索ができる
よくある単語一致検索は、入力した単語が含まれていないと結果を得ることができません。しかし、時間がたつと内容は覚えていても、どの単語を使って検索したらいいのかが思い出せないことがあります。類似度を用いることで、入力した単語やフレーズに似た意味を持つものを基に検索ができるため、表現が異なっていても関連する情報を効率よく検索できます。例えば、ユーザーが「天気がいい」と検索した場合でも、「晴れ」「青空」など、言い回しが異なるが意味が似ている結果を得られるため、検索が直感的に行えるようになります。

２，クラスタリング
文章間の類似度を得ることによって、文章を内容で自動的にクラスタリングすることが出来ます。例えば、フィードバックを得る際に貰った意見を内容でまとめて効率的に振り替えるなどの活用も考えられます。

等々、これら以外にも多くの利用方法が考えられます。

文章間の類似度の測り方

A「今日は天気がいい。」
B「雲一つない綺麗な青空だ。」
この2つの文章は言い方こそ違いますが、意味はとても似ています。この 「文章が似ている」 という感覚は人間なら多く人が持っているものですが、実はコンピュータでも同じようなことが可能です。では、0,1しかないコンピュータがどのようにして「文章が似ている」ことを判断するのでしょうか。
もちろんコンピュータは人間のように感情を持っているわけではないので、全てを数値化して計算をしています。文章間の類似度を測定する基本的な考え方は、 文章を何らかの形で数値化し、その数値間の距離や近さを計算する ことにあります。例えるなら、地図上で二つの地点間の距離を測るのと同じイメージです。
まずは、文章間の類似度を測る大まかな流れを説明します。

① 文章をベクトルに変換する
② ベクトル同士の類似度を測定する

以上です。次に、それぞれでどのような操作が行われているのかについて確認して行きます。

文章をベクトルに変換する

ここに関しては筆者自身があまり詳しくなく、なんか意味を考慮して上手くベクトルに変換してくれているらしい 程度の理解しかありません。
自然言語処理に関しては、以下の記事が大変分かりやすく、かつ全体像を把握できる内容となっています。
https://qiita.com/AxrossRecipe_SB/items/fd1e6e893e3f3fb50d2c

ここでは、私が現在知っている内容（ほぼ無いに等しいですが）を簡単にまとめておきます。

Sentence Embeddingは、単語レベルの情報を集約するだけでなく、文章が持つ文脈やニュアンスといった、より深い意味合いを捉えることを目指します。これにより、表現が異なる文章であっても、意味が近ければ ベクトル空間上で近い位置に配置 されるようになります。

近年では、Sentence Embeddingを利用した様々な手法が提案されており、ここでは名前だけ紹介しておきます。
1, Doc2Vec
2, USE
3, SBERT (Sentence Transformers)

特に、最後のSBERTに関連するBERTについては、下記記事が大変分かりやすくまとめられています。事前学習方法からファインチューニング、実験結果までかなり丁寧に書かれている良記事です。
https://qiita.com/omiita/items/72998858efc19a368e50#132-bert%E3%81%AE%E4%BA%8B%E5%89%8D%E5%AD%A6%E7%BF%92

ベクトル化と埋め込み(embedding)は意味が違います！

• ベクトル化
  単語の出現頻度などを数値化するだけで、意味的なつながりまでは表現できない
• 埋め込み
  文章全体の意味を保持したまま、ベクトルに変換する

詳しくは、以下の記事を参照してください。
https://blog.since2020.jp/ai/what-is-embedding/

② ベクトル同士の類似度を測定する

さて、無事に？文章の意味まで考慮したベクトルが得られたところでベクトル同士の類似度を測っていきます。文章間の類似度を測る手法も複数あるのですが、今回は 「コサイン類似度」と「ユークリッド距離」 の2つについて説明していきます。

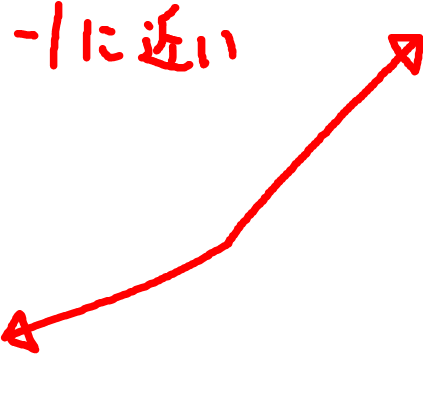
１，コサイン類似度

コサイン類似度は、2つのベクトル間の方向の一致度を調べるものです。意味が似ているベクトルは同じような方向を指すので、同じような内容なら1に、意味が離れるほど-1 に近くなります。また、以下の式において$\mathbf{A}$ $\cdot$ $\mathbf{B}$ は内積、$||\mathbf{A}||$ と $||\mathbf{B}||$ は各ベクトルのノルム（大きさ）を表しています。

\text{Cosine Similarity} = \frac{\mathbf{A} \cdot \mathbf{B}}{||\mathbf{A}|| \times ||\mathbf{B}||}

２，ユークリッド距離

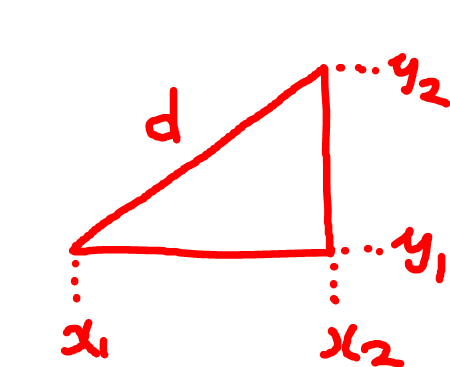
ユークリッド距離とは、2つのベクトル間の距離を求めるものです。
n次元空間において、2つのベクトル A = (a₁, a₂, ..., aₙ) と B = (b₁, b₂, ..., bₙ) のユークリッド距離 d は、以下の式で表せます​

d = √[(a₁ - b₁)² + (a₂ - b₂)² + ... + (aₙ - bₙ)²]​

中学校の時に習った三平方の定理を思い出してもらえるとやっていることが分かるかと思います。ここで扱っているベクトルは複数次元を持ちますので、三平方のn次元版です。

最後に

SentenceTransformerにも様々なモデルがあり、私が試した中ではstsb-xlm-r-multilingualが一番良い結果を出していました。これは、768次元で意味をベクトル空間上にマッピングし、しかも、多言語に対応しています。そのため、日本語と英語間の意味的な文章の類似度を測定することもできるため大変面白いです。
各モデルの詳細な実験については、下記記事をご覧ください。
https://zenn.dev/welmo/articles/a79b8b45573383

以下にGoogle Colabのリンクを載せておきます。簡単に文章間の類似度を測定することが出来ますので、興味のあるかたは是非試してみてください。
https://colab.research.google.com/drive/1sMKhvPMAEPdKrSzAMRNGnIF2bkLnUCdc?usp=sharing