問.
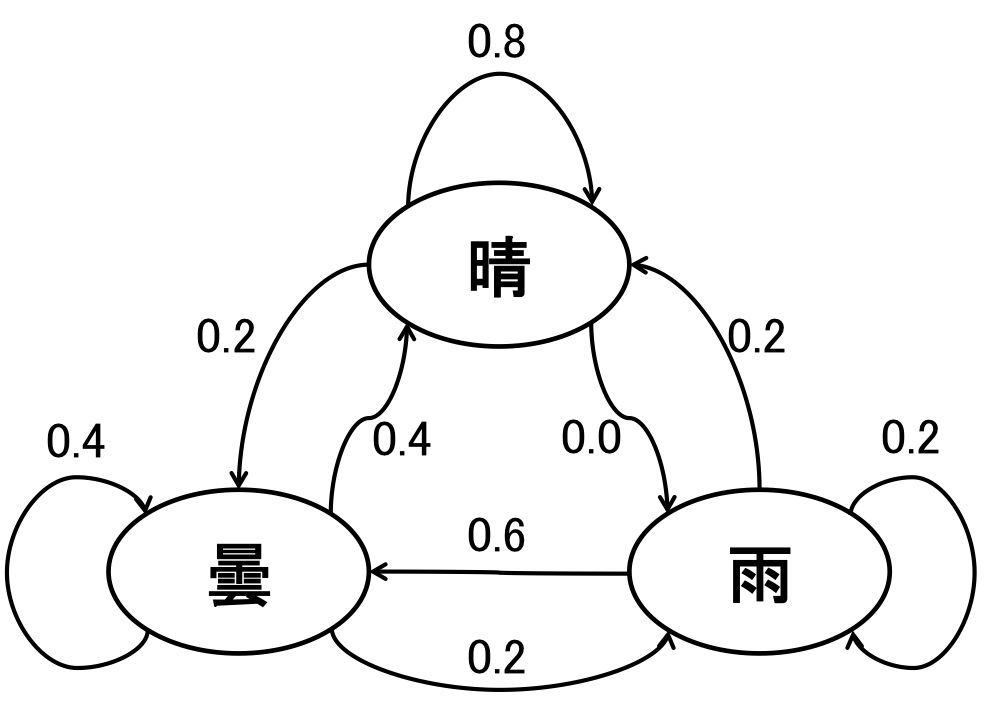
毎日の天気が以下の表に示すマルコフ連鎖となっている地域がある.
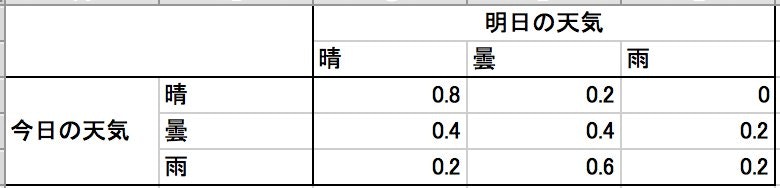
a) 一日目が晴だったとき,二日目は曇,三日目は曇,四日目が雨と遷移する確率
b) 上の表に従って「天気」を生成するシミュレータを書け
c) 作成したシミュレータを用いて,ある日が晴,曇,雨となる確率を求めよ(定常状態確率)
d) c)で求めた確率を方程式によって導け
e) 定常分布のエントロピーを求めよ
f) ベイズ則を用いて,今日の天気から明日の天気の確率を求めた表を作成せよ
e) 上記の状態遷移確率は夏にしか適用できず,他の季節は別の状態遷移確率が必要な場合,確率過程のマルコフ性を破ることになるだろうか?
答.
以下,事象$S$をそれぞれ次のように文字で表す.
$S_{TdySny}$ : 今日が晴
$S_{TdyCdy}$ : 今日が曇
$S_{TdyRny}$ : 今日が雨
$S_{TrwSny}$ : 明日が晴
$S_{TrwCdy}$ : 明日が曇
$S_{TrwRny}$ : 明日が雨
$S_{YdySny}$ : 昨日が晴
$S_{YdyCdy}$ : 昨日が曇
$S_{YdyRny}$ : 昨日が雨
また,$p(S)$は,事象$S$が起こる確率を表す.
$p(S_0, S_1)$は,事象$S_0$と事象$S_1$が起こる確率(同次確率)であり,$p(S_1|S_0)$は,事象$S_0$のときに事象$S_1$が起こる確率(事後確率)である.
a)一日目が晴だったとき,二日目は曇,三日目は曇,四日目が雨と遷移する確率
これは単純に同次確率.
今日が晴だったとき,明日が曇になる確率 x 今日が曇だったとき,明日が曇になる確率 x 今日が曇だったとき,明日が雨になる確率.それぞれの確率を表から拾う.
\begin{align}
p&(S_{TrwCdy}|S_{TdySny}) \cdot p(S_{TrwCdy}|S_{TdyCdy}) \cdot p(S_{TrwRny}|S_{TdyCdy}) \\
&= 0.2 \cdot 0.4 \cdot 0.2\\
&= \frac{2}{125} = 0.016
\end{align}
b) 上の表に従って「天気」を生成するシミュレータを書け
# !/usr/local/bin/python
import random
import collections
(
Sunny,
Cloudy,
Rainy,
) = range(0, 3)
Weather = ["Sunny", "Cloudy", "Rainy"]
def genWeather(today):
tomorrow = 0
rnd = random.random()
if today == Sunny:
if rnd < 0.8:
tomorrow = Sunny
else:
tomorrow = Cloudy
elif today == Cloudy:
if rnd < 0.4:
tomorrow = Sunny
elif rnd < 0.8:
tomorrow = Cloudy
else:
tomorrow = Rainy
else: # today == Rainy
if rnd < 0.2:
tomorrow = Sunny
elif rnd < 0.8:
tomorrow = Cloudy
else:
tomorrow = Rainy
return tomorrow
if __name__ == '__main__':
aryWeather = []
today = Sunny
for i in range(0, 100000):
tomorrow = genWeather(today)
aryWeather.append(tomorrow)
today = tomorrow
cnt = collections.Counter(aryWeather)
for k, v in cnt.items():
print Weather[k], v, v/100000.
c) 作成したシミュレータを用いて,ある日が晴,曇,雨となる確率を求めよ(定常状態確率)
b)で作成したシミュレータの出力例
Sunny 644205 0.644205
Cloudy 284507 0.284507
Rainy 71288 0.071288
よって,晴の確率$64.4[%]$,曇の確率$28.5[%]$,雨の確率$7.1[%]$.
d) c)で求めた確率を方程式によって導け
マルコフ連鎖の定常分布を求める問題.
求めたい定常分布(時間が経過しても確率過程の分布が変化しない場合)を$\boldsymbol{\alpha} = (\alpha_{S_{Sny}}, \alpha_{S_{Cdy}}, \alpha_{S_{Rny}})$とするとき,逆説的に以下の連立方程式が成り立つ.
\left\{
\begin{array}{l}
\begin{align}
\alpha_{S_{Sny}} &= 0.8 \alpha_{S_{Sny}} + 0.4 \alpha_{S_{Cdy}} + 0.2 \alpha_{S_{Rny}}\\
\alpha_{S_{Cdy}} &= 0.2 \alpha_{S_{Sny}} + 0.4 \alpha_{S_{Cdy}} + 0.6 \alpha_{S_{Rny}}\\
\alpha_{S_{Rny}} &= 0.0 \alpha_{S_{Sny}} + 0.2 \alpha_{S_{Cdy}} + 0.2 \alpha_{S_{Rny}}\\
1 &= \alpha_{S_{Sny}} + \alpha_{S_{Cdy}} + \alpha_{S_{Rny}}
\end{align}
\end{array}
\right.
この連立方程式を解くと,$\alpha_{S_{Sny}} = \frac{9}{14}$,$\alpha_{S_{Cdy}} = \frac{2}{7}$,$\alpha_{S_{Rny}} = \frac{1}{14}$を得る.
よって,それぞれの天気の定常状態確率は$p(S_{Sny}) = \frac{9}{14} \fallingdotseq 64.3[%]$,$p(S_{Cdy}) = \frac{2}{7} \fallingdotseq 28.6[%]$,$p(S_{Rny}) = \frac{1}{14} \fallingdotseq 7.14[%]$である.
参考:東京農工大学 情報工学科 堀田研究室 情報理論 第4回 確率過程
e) 定常分布のエントロピーを求めよ
$n$個の互いに排反で生起確率$p(S_i)$の総和が1の事象系(完全事象系)のエントロピーは,以下の式で計算できる.
$$H = -\sum_{k=1}^{n} p_k \log_2 p_k$$
晴,曇,雨の3事象なので,
$$H = -(p(S_{Sny}) \log_2 p(S_{Sny}) + p(S_{Cdy}) \log_2 p(S_{Cdy}) + p(S_{Rny}) \log_2 p(S_{Rny}))$$
d)で求めた定常状態確率を代入して,
$$H = -(\frac{9}{14} \log_2 \frac{9}{14} + \frac{2}{7} \log_2 \frac{2}{7} + \frac{1}{14} \log_2 \frac{1}{14}) \fallingdotseq 1.2[bit]$$
参考:東京農工大学 情報工学科 堀田研究室 情報理論 第5回 情報量とエントロピー
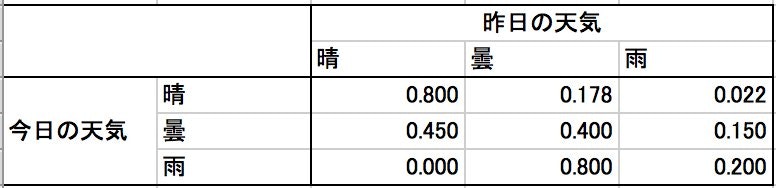
f) ベイズ則を用いて,今日の天気から明日の天気の確率を求めた表を作成せよ
まずは,今日が晴だった場合に昨日が晴であった確率を求める.
$$p(YdySny|TdySny) = \frac{p(TdySny|YdySny) \cdot p(YdySny)}{p(TdySny)}$$
ベイズの定理より,上式が成り立つ.昨日の確率には定常状態確率を代入する.
\begin{align}
p(YdySny|TdySny) &= \frac{p(TdySny|YdySny) \cdot p(YdySny)}{p(TdySny)}\\
&= \frac{p(TdySny|YdySny) \cdot p(Sny)}{p(TdySny|YdySny)p(Sny) + p(TdySny|YdyCdy)p(Cdy) + p(TdySny|YdyRny)p(Rny)}\\
&= \frac{\frac{8}{10} \cdot \frac{9}{14}}{\frac{8}{10} \cdot \frac{9}{14} + \frac{4}{10} \cdot \frac{2}{7} + \frac{2}{10} \cdot \frac{1}{14}} \\
&= \frac{4}{5} = 0.800
\end{align}
次に,今日が晴だった場合に昨日が曇であった確率を求める.今日が晴である確率$p(TdySny)$は上で計算したものを利用する.
\begin{align}
p(YdyCdy|TdySny) &= \frac{p(TdySny|YdyCdy) \cdot p(YdyCdy)}{p(TdySny)}\\
&= \frac{p(TdySny|YdyCdy) \cdot p(Cdy)}{p(TdySny)}\\
&= \frac{\frac{4}{10} \cdot \frac{4}{14}}{\frac{90}{140}} \\
&= \frac{8}{45} \fallingdotseq 0.178
\end{align}
次に,今日が晴だった場合に昨日が雨であった確率を求める.これまでと同様に,今日が晴である確率$p(TdySny)$は上で計算したものを利用する.
\begin{align}
p(YdyRny|TdySny) &= \frac{p(TdySny|YdyRny) \cdot p(YdyRny)}{p(TdySny)}\\
&= \frac{p(TdySny|YdyRny) \cdot p(Rny)}{p(TdySny)}\\
&= \frac{\frac{2}{10} \cdot \frac{1}{14}}{\frac{90}{140}} \\
&= \frac{1}{45} \fallingdotseq 0.0222
\end{align}
以下,同様に今日が曇だった場合と雨だった場合の昨日の天気の確率をそれぞれ求める.
\begin{align}
p(YdySny|TdyCdy) &= \frac{p(TdyCdy|YdySny) \cdot p(YdySny)}{p(TdyCdy)}\\
&= \frac{p(TdyCdy|YdySny) \cdot p(Sny)}{p(TdyCdy|YdySny)p(Sny) + p(TdyCdy|YdyCdy)p(Cdy) + p(TdyCdy|YdyRny)p(Rny)}\\
&= \frac{\frac{2}{10} \cdot \frac{9}{14}}{\frac{2}{10} \cdot \frac{9}{14} + \frac{4}{10} \cdot \frac{2}{7} + \frac{6}{10} \cdot \frac{1}{14}} \\
&= \frac{9}{20} = 0.450
\end{align}
\begin{align}
p(YdyCdy|TdyCdy) &= \frac{p(TdyCdy|YdyCdy) \cdot p(YdyCdy)}{p(TdyCdy)}\\
&= \frac{p(TdyCdy|YdyCdy) \cdot p(Cdy)}{p(TdyCdy)}\\
&= \frac{2}{5} = 0.400
\end{align}
\begin{align}
p(YdyRny|TdyCdy) &= \frac{p(TdyCdy|YdyRny) \cdot p(YdyRny)}{p(TdyCdy)}\\
&= \frac{p(TdyCdy|YdyRny) \cdot p(Rny)}{p(TdyCdy)}\\
&= \frac{3}{20} = 0.150
\end{align}
\begin{align}
p(YdySny|TdyRny) &= \frac{p(TdyRny|YdySny) \cdot p(YdySny)}{p(TdyRny)}\\
&= \frac{p(TdyRny|YdySny) \cdot p(Sny)}{p(TdyRny|YdySny)p(Sny) + p(TdyRny|YdyCdy)p(Cdy) + p(TdyRny|YdyRny)p(Rny)}\\
&= \frac{\frac{0}{10} \cdot \frac{9}{14}}{\frac{0}{10} \cdot \frac{9}{14} + \frac{2}{10} \cdot \frac{2}{7} + \frac{2}{10} \cdot \frac{1}{14}} \\
&= \frac{0}{10} = 0.000
\end{align}
\begin{align}
p(YdyCdy|TdyRny) &= \frac{p(TdyRny|YdyCdy) \cdot p(YdyCdy)}{p(TdyRny)}\\
&= \frac{p(TdyRny|YdyCdy) \cdot p(Cdy)}{p(TdyRny)}\\
&= \frac{4}{5} = 0.800
\end{align}
\begin{align}
p(YdyRny|TdyRny) &= \frac{p(TdyRny|YdyRny) \cdot p(YdyRny)}{p(TdyRny)}\\
&= \frac{p(TdyRny|YdyRny) \cdot p(Rny)}{p(TdyRny)}\\
&= \frac{1}{5} = 0.200
\end{align}
e) 上記の状態遷移確率は夏にしか適用できず,他の季節は別の状態遷移確率が必要な場合,確率過程のマルコフ性を破ることになるだろうか?
確率過程がマルコフ性を持つとは,「ある時刻$t$における事象の生起する確率が_直前の事象のみ_に依存する」であるから,他の季節に別の状態遷移確率となったとしても,その状態遷移が昨日の天気に依存している限り,この気象がマルコフ性を持っていると言える.(だよね?)