前回、株式の時系列データを分析する話で、後半にちょっとだけ機械学習の話をしました。今日は機械学習ライブラリ scikit-learn に触れます。
scikit-learn といえば以前にも簡単なクラスタリングの例をあげたり、サポートベクトルマシンやクラスタリングで問題を解く、 TF-IDF を計算する、回帰モデルの可視化、 DBSCAN によるクラスタリングといったことをしてきましたが、あらためてライブラリの機能を整理します。
機械学習と言うと難しい数学を駆使するイメージがつきまといますが、完成度の高いライブラリを使えば利用者が機械学習の手法そのものを実装しなくても利用することはできます。もちろん手法の内容に対する理解は必要ですが、せっかく scikit-learn という事実上デファクトとも言えるライブラリが存在するのですから、これを使うところから入門していくのが良いかと思います。
以前にもこの話は書きましたけれども Python を利用する最大のメリットは、このように統計や機械学習など科学計算やデータ分析に関するライブラリがきわめて充実していることが挙げられます。数値計算全般に関しても NumPy と SciPy という非常に優れたライブラリがあり、データフレームの扱いについても pandas が、可視化についても matplotlib があります。同じことを他の言語 (Ruby や Scala など) でやろうとすると相当に苦労するというかほぼ不可能ですので選択肢としてはまずないでしょう。統計用の言語としては他に R がありますが、 Python のほうが一般的な言語でもあるためより言語としての完成度が高く、 R のほうが既存の資産が充実しているという特徴があるかと思います。
機械学習の基本的な手順
まずは手順を整理しましょう。
- データの入手
- データ前処理 (加工、整形、尺度の変換などにより素性を生成する)
- 手法の選択
- パラメーターの選択
- モデルの学習
- モデルの評価
- チューニング (3. から 6. を繰り返す)
基本的な手順は上記の通りとなります。
手法の選択
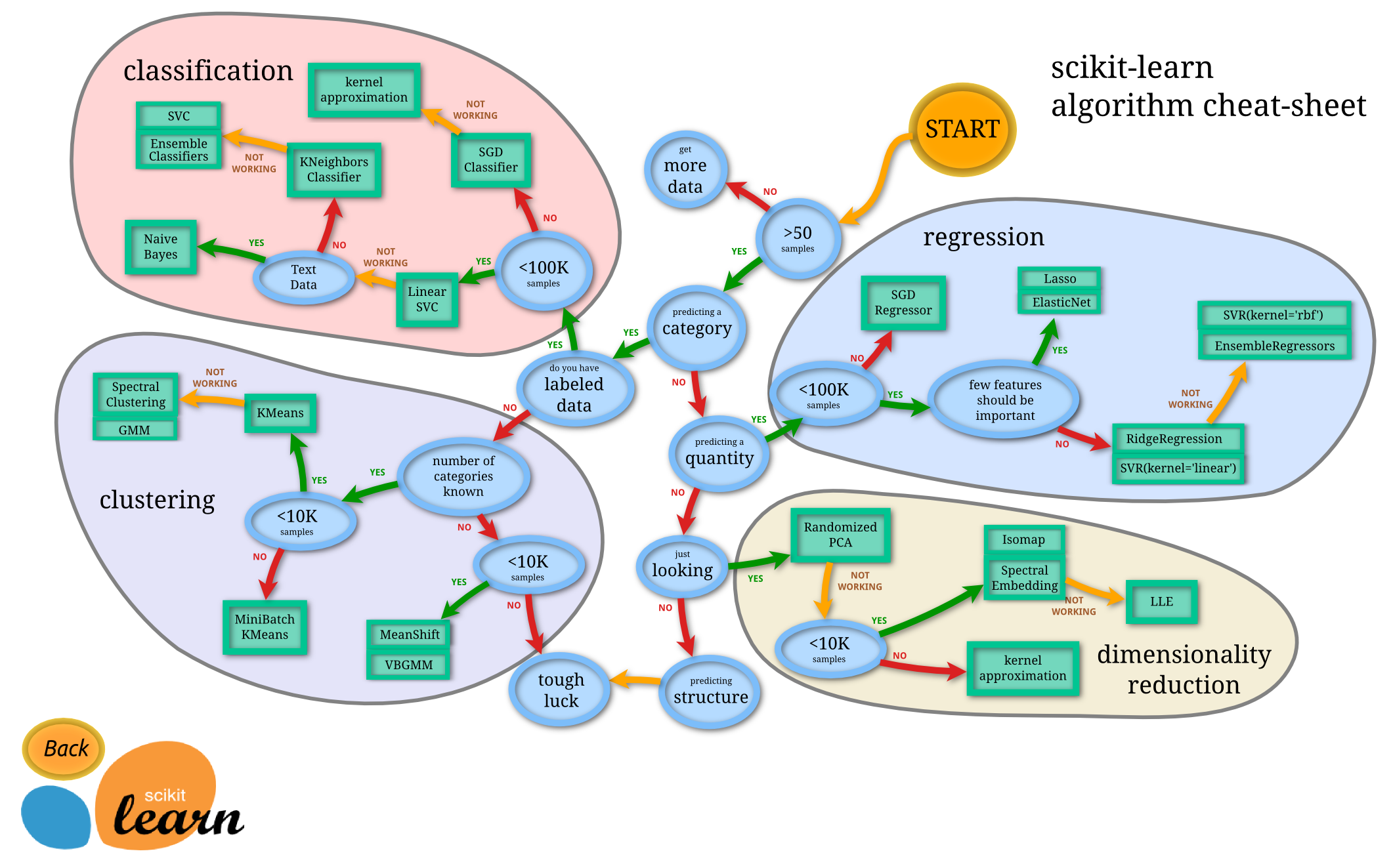
scikit-learn で出来ることはチートシートを見るのが一番です。
オリジナルは本家にあります。
Choosing the right estimator
http://scikit-learn.org/stable/tutorial/machine_learning_map/
ここから各手法の説明に飛べますので重宝します。
できることを整理すると次の通りです。
- 分類 (Classification) - ラベルとデータを学習し、データに対してのラベルを予測する。
- 回帰 (Regression) - 実数値をデータで学習して、実数値を予測する。
- クラスタリング (Clustering) - データの似ているもの同士をまとめて、データの構造を発見する。
- 次元削減 (Dimensionality reduction) - データの次元を削減して、要因を発見 (主成分分析など) したり、他の手法の入力に使う (次元の呪い回避)。
ではひとつひとつ特長を追っていきましょう。
分類 (Classification)
SVM (サポートベクトルマシン、線形サポートベクトルマシン)
汎化性能が高く、カーネル関数を選択できるのでさまざまなデータに対応できます。
K 近傍法
単純なわりに高い精度を誇ります。
ランダムフォレスト
過学習を考慮しなくてよい、並列計算しやすいといった特長があります。
回帰 (Regression)
回帰
普通の線形回帰です。
ラッソ回帰
少ない変数でモデルを作るが、使わない変数があることを仮定しています。
リッジ回帰
多重共線性の影響を受けにくく、ラッソ回帰より変数選択力が弱いという特長があります。
SVR
カーネルで非線形性を取りこむことができます。
クラスタリング
K 平均法 (KMeans)
クラスタの数を k 個とあらかじめ指定する代表的なクラスタリング手法です。単純で高速に動作します。
混合ガウス分布 (GMM)
クラスタの所属確率を求めることができます。正規分布を仮定します。
平均変位法 (MeanShift)
カーネル密度推定を用いたロバストでノンパラメトリックな手法です。設定するカーネル幅 (半径 h ) によって自動的にクラスタの数が決まります。入力点群すべてに対して最急降下法の原理を用いて半径 h の円を考え中心点を計算するのでコストが高くなりがちです。
画像のセグメンテーション、エッジ保存の画像の平滑化といった場面にも応用される手法です。
カーネル幅 h を無限大にしたミーンシフトクラスタ解析が k 平均法であると解釈することもできます。
次元削減 (Dimensional Reduction)
主成分分析 (PCA)
疎行列も扱え速いという特長があります。正規分布を仮定します。
非負値行列因子分解 (NMF)
非負行列のみ使えますが、より特徴を抽出しやすいこともあります。
その他に線形判別 (LDA) や Deep Learning なども使えます。
BLAS と LAPACK
scikit-learn が依存するライブラリです。これは scikit-learn だけでなく SciPy だとか C や Fortran などをはじめとする他の言語のプログラムなどさまざまな数値計算ソフトが BLAS と LAPACK に依存しています。 GNU/Linux ディストリビューションにパッケージとして用意されていることがほとんどです。さまざまな言語から利用することができ歴史もありますので、計算機で線形代数演算をおこなうものとしては事実上の標準です。
- BLAS - 線形代数ライブラリの標準仕様です。
- LAPACK - BLAS を基礎として高度な線形代数を解きます。
LAPACK は、具体的には連立一次方程式、最小二乗法、固有値問題、特異値問題、行列 (LU) 分解、コレスキー分解、 QR 分解、特異値分解、 Schur 分解、一般化 Schur 分解、条件数の推定ルーチン、逆行列計算、またさまざまなサブルーチン群を提供します。
BLAS の実装にはさまざまなものがありますが代表的なものは以下の通りです。
- Intel MKL - MATLAB などで使われる。有償だがとても速い。
- OpenBLAS - BSD ライセンスで無償で使える。
それほど速度を気にしないのであればとりあえず OpenBLAS を使うことが多いのではないかと思います。
パラメータの選択
良いパラメータを効率よくおこなう方法が交差検定 (クロスバリデーション) やグリッドサーチと呼ばれる方法です。これらを駆使してモデルの学習と評価を繰り返していくわけですが、このあたりはまた後で触れます。
まとめ
今回は機械学習ライブラリ scikit-learn に実装されている手法という観点から、代表的な機械学習の手法についてまとめました。 scikit-learn は非常に充実した品質の高いライブラリですので、まずはここを押さえておくと理解が進むかと思います。