CodeIQ の問題を解く
一年以上前の問題ですが CodeIQ に掲載された機械学習の問題をひとつ解いてみます。
「機械学習基礎」簡単な問題を解いて理解しよう!前篇
http://next.rikunabi.com/tech/docs/ct_s03600.jsp?p=002315
これの第一問にチャレンジです。
線形分離問題
問題
週末に海賊船で催されたPRML読書会に参加したN君は、船内に山のように積まれた金銀財宝に目を奪われました。 近くにあった宝箱の1つを開けてみると、きらきらと輝くコインが何枚も入っていました。
手に取ってみるとどれもずっしりと重みがあります。金貨に違いありません。
好きなだけ持って帰ってよいと言われ、勉強会帰りに何枚か鞄に詰め込んで帰ることにしました。
家に帰ってから少し冷静になったN君は「気前よく配っていたけれど、この金貨は本物なのだろうか」と疑い始めました。
鞄には20枚の金貨が入っていましたが、友人のアルキメデスに計測してもらったところ、20枚とも体積も重さも異なりました。
ネットで検索してみたところ、金貨の体積と重さと真贋のデータを得られました。
このデータを参考に、貰ってきた金貨の真贋を見分けてください。
元記事にある通り、綺麗に線形分離できそうなデータです。
いつも通り scikit-learn を使って解きます。
データの読み込み
import numpy as np
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt
auth = np.genfromtxt('CodeIQ_auth.txt', delimiter=' ')
# 教師データ
train_X = np.array([[x[0], x[1]] for x in auth])
# 教師データのラベル
labels = [int(x[2]) for x in auth]
# テストデータ
test_X = np.genfromtxt('CodeIQ_mycoins.txt', delimiter=' ')
データ可視化
まずはデータをプロッティングしてみます。
fig = plt.figure()
ax1 = fig.add_subplot(2,1,1)
ax2 = fig.add_subplot(2,1,2)
# 教師データから正解を抽出
correct = np.array([[x[0], x[1]] for x in auth if x[2] == 1]).T
# 同じくニセモノを抽出
wrong = np.array([[x[0], x[1]] for x in auth if x[2] == 0]).T
# これらを散布図にプロッティングする
ax1.scatter(correct[0], correct[1], color='g')
ax1.scatter(wrong[0], wrong[1], color='r')
ax2.scatter(train_X.T[0], train_X.T[1], color='b')
ax2.scatter(test_X.T[0], test_X.T[1], color='r')
plt.legend(loc='best')
plt.show()
plt.savefig("image.png")
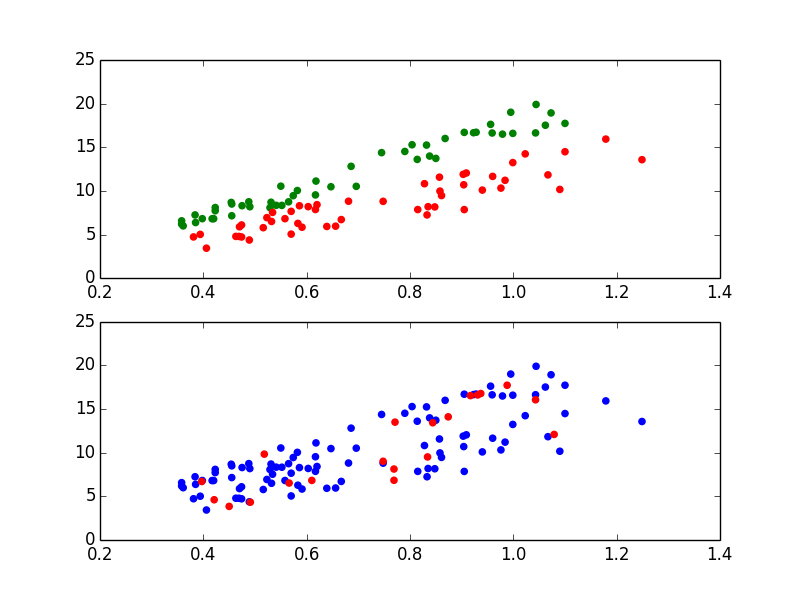
上図の緑が正解、赤がニセモノの金貨です。元記事のプロット通りですね。
下図は真贋データ (青) に対する、手に入れた金貨 (赤) の分布となります。
解法
線形分離問題なので LinearSVC を使います。
clf = LinearSVC(C=1)
# 訓練
clf.fit(train_X, labels)
# 分類
results = clf.predict(test_X)
for result, feature in zip(results, test_X):
print(result, feature)
結果
1 [ 0.988 17.734]
0 [ 0.769 6.842]
0 [ 0.491 4.334]
1 [ 0.937 16.785]
1 [ 0.844 13.435]
0 [ 0.834 9.518]
1 [ 0.931 16.62 ]
1 [ 0.397 6.705]
1 [ 0.917 16.544]
0 [ 0.45 3.852]
0 [ 0.421 4.612]
1 [ 0.518 9.838]
1 [ 0.874 14.113]
0 [ 0.566 6.529]
0 [ 0.769 8.132]
1 [ 1.043 16.066]
0 [ 0.748 9.021]
0 [ 0.61 6.828]
0 [ 1.079 12.097]
1 [ 0.771 13.505]
左側の 0 1 が解答になります。というわけで、例と同じ解答を得られるに至りました。