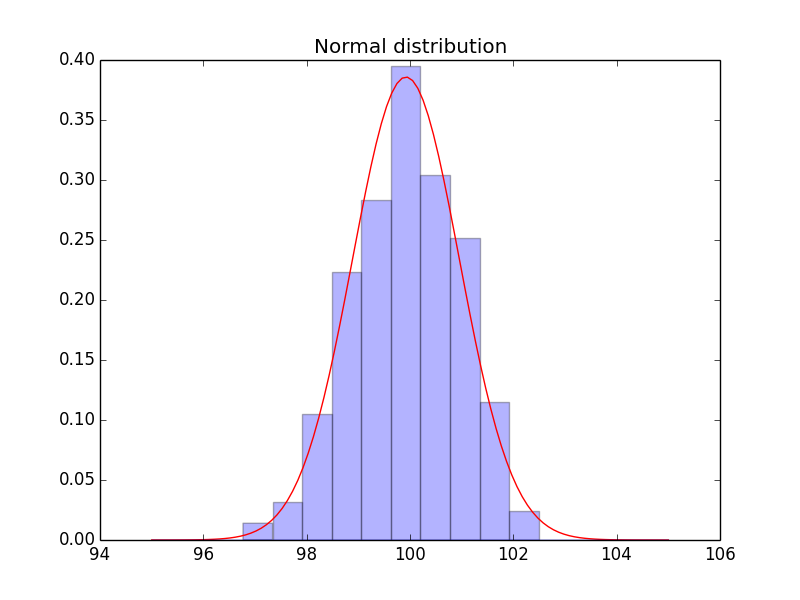
正規分布とそのフィッティング
すでに何度か登場している線形回帰ではデータの分布にフィットする線の理論式を最小二乗法にて求めました。線形回帰など今までに登場したさまざまな分析の多くで正規分布が仮定されます。
フィッティングに欠かせない手法とも言える最小二乗法は、プロットされたデータを理論式にフィッティングさせることによって理論式中に含まれる定数がいくらであるか、そこからさまざまな情報を得ることができます。たとえば各点にフィットする直線の傾きを求めたいとき、正規分布を仮定する分布の統計量を求めたいときなど色々な場面で使われます。
正規分布 (normal distribution) はまたの名を ガウス分布 (Gaussian distribution) と言い、平均値の付近にピークが集積するデータの分布を表した連続変数に関する確率分布であることは過去の記事でも説明しました。正規分布に対する近似曲線(フィッティングカーブ)の関数を求めることをガウシアンフィッティングと言います。例によって SciPy の強力な数学関数を駆使することでガウシアンフィッティングは容易に実現できます。
正規分布に近似したサンプルを得る
まずは正規分布に近似したサンプルを求めます。次のように 100 を平均とした 500 件のデータを生成します。
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
import pylab as plb
# 正規分布に近似したサンプルを得る
# 平均は 100 、標準偏差を 1 、サンプル数を 500 とする
sample = norm.rvs(loc=100,scale=1,size=500)
print (sample) # =>
#[ 101.02975418 99.95689958 100.8338816 99.32725219 101.50090014
# 99.29039034 101.64895275 100.45222206 100.22525394 98.8036744
# 100.73576941 99.32705948 100.52278215 102.38383015 98.28409264
# 99.22632512 100.84625978 99.69653993 100.9957202 97.97846995
# 99.49731157 100.89595798 101.3705089 101.15367469 100.26415751
# 99.14143516 100.21385338 99.69883406 99.68494407 100.70380005
# 100.73544699 100.3434308 99.50291518 99.61483734 100.92201666
# 100.98639356 100.36362462 98.39298021 98.39137284 101.54821395
# 100.2748115 100.78672853 99.79335862 98.8123562 100.57942641
# 100.03497218 99.98368219 100.45979578 99.32342998 98.08908529
# ...
フィッティングと可視化
フィッティングは 1 つのメソッドですみます。
param = norm.fit(sample)
print (param)
# => (99.92158820017579, 1.0339291481971331)
パラメータが求まりましたのであとはこれをプロットすれば OK です。
x = np.linspace(95,105,100)
pdf_fitted = norm.pdf(x,loc=param[0], scale=param[1])
pdf = norm.pdf(x)
plt.figure
plt.title('Normal distribution')
plt.plot(x, pdf_fitted, 'r-', x,pdf, 'b-')
plt.hist(sample, normed=1, alpha=.3)
plt.show()
plt.savefig("image.png")
うまくいきました。
最小二乗法を使って工学上などの問題を解析した例などは枚挙に暇がありません。また、正規分布を仮定したモデルでその前提がゆらぐとデータ分析工程が台無しになりますので、確率分布や検定についてよく理解しておくことが大切です。