昨日の続きで統計学の実践的な手法を追っていきます。今日はロジスティック回帰についてです。
参考文献
書籍をお持ちの方は最強である p189 実践編 p221 あたりを参照してください。 (後者のほうが詳しいです)
またロジスティック回帰の説明としては
概要については
ロジスティック回帰の考え方・使い方 - TokyoR #33
http://www.slideshare.net/horihorio/tokyo-r33-logi
説明については
ロジスティック回帰と変数選択 (三重大学・奥村先生)
http://oku.edu.mie-u.ac.jp/~okumura/stat/140921.html
また実務における例としては
回帰分析とその応用③ ~ロジスティック回帰分析
http://www.gixo.jp/blog/2492
マーケターのためのデータマイニング・ヒッチハイクガイド
第10回:ロジスティック回帰分析
http://jpn.teradata.jp/library/ma/ins_1310a.html
あたりが詳しくわかりやすいと思います。
ロジスティック回帰の使いどころ
ロジスティック回帰は true か false という二値論理に関するアウトカムを分析するための回帰分析であると言われています。 (前回の表を参照)
統計の分野では一般的な方法ですが、機械学習の分野でも PRML 4 章線形識別モデル 4.3.2 ロジスティック回帰 (p204)として登場します。こちらでは名前は回帰ですが、実際は分類のためのモデルであると強調されています。クラス C1 の事後確率が特徴ベクトル Φ の線形関数のロジスティックシグモイド関数として書けることを利用したモデルです。
以前に挙げた線形回帰と比較すると、ごく単純な線形回帰である単回帰分析では直線に回帰するのに対し、あてはめのイメージが対数オッズにもとづいた曲線となるところに特徴があります。
業務上扱いたいアウトカムは「この人は一度でも来店したことがあるかどうか」「この会員は解約するのかどうか」というふうに 0 か 1 かで表現できる論理だったりすることが多いです。
たとえば前回も登場したケースコントロール調査のような例で、似たような条件なのに病気になった人とならなかった人の間でどのような違いがあるのか、このようなことをより深く調べていこうといったときに、重回帰分析以上のあてはまりを見せることがあります。
実践してみる
単純な例では奥村先生のページのロジスティック回帰の例がわかりやすいです。
y = 入試の合否 x1 = 内申点 x2 = 模試の偏差値としたときに
| 入試の合否(y) | 内申点(x1) | 偏差値(x2) |
|---|---|---|
| 0 | 3.6 | 60.1 |
| 1 | 4.1 | 52.0 |
| 0 | 3.7 | 62.5 |
| 0 | 4.9 | 60.6 |
| 1 | 4.4 | 54.1 |
| 0 | 3.6 | 63.6 |
| 1 | 4.9 | 68.0 |
| 0 | 4.8 | 38.2 |
| 1 | 4.1 | 59.5 |
| 0 | 4.3 | 47.3 |
これをロジスティック回帰すると
# データを読み込む
data1 <- read.csv("data1.csv", header=TRUE)
# ロジスティック回帰
mylogit = glm(y ~ x1 + x2, data=data1,
family=binomial(link="logit"))
# サマリーを見る
summary(mylogit)
# =>
# Call:
# glm(formula = y ~ x1 + x2, family = binomial(link ="logit"), data = data1)
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -1.4754 -0.8584 -0.8007 1.1905 1.5719
# Coefficients:
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -9.44589 9.12237 -1.035 0.300
# x1 1.27158 1.49423 0.851 0.395
# x2 0.06424 0.08739 0.735 0.462
# (Dispersion parameter for binomial family taken to be 1)
# Null deviance: 13.460 on 9 degrees of freedom
# Residual deviance: 12.345 on 7 degrees of freedom
# AIC: 18.345
# Number of Fisher Scoring iterations: 4
# フィットされた値を見る
fitted(mylogit)
# =>
# 1 2 3 4 5 6 7 8 9 10
# 0.2675020 0.2907201 0.3260736 0.6632579 0.4072105 0.3137831 0.7600997 0.2914609 0.3988916 0.2810008
つまりは以下の式で予測される、またフィットされた値もわかるというわけです。
logit(\pi) = -9.44589 + 1.27158x_{1} + 0.06424x_{2}
※ ただし有意ではありません
可視化する
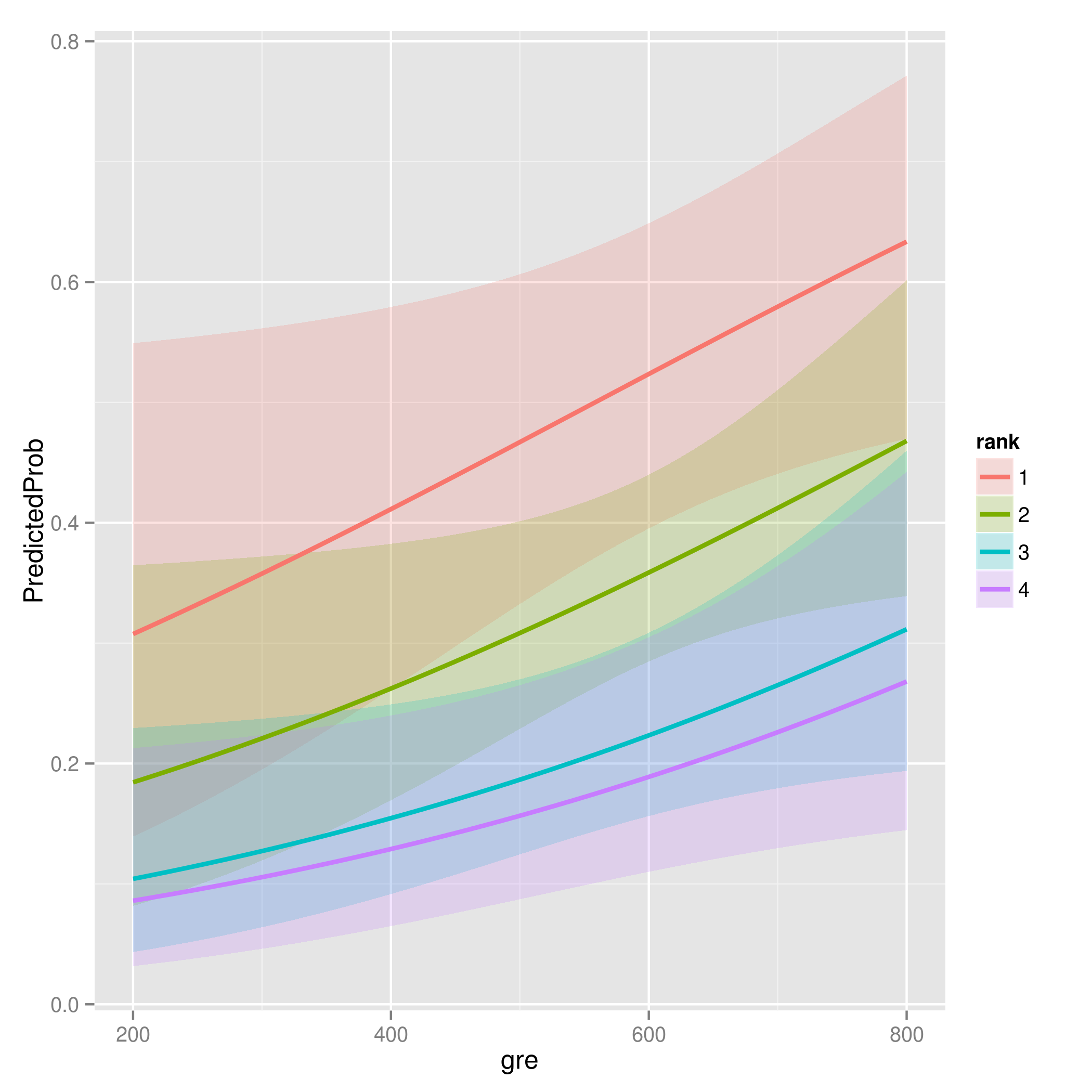
カリフォルニア大学ロサンゼルス校のページに掲載されているこちらの例に沿って R で可視化した例を紹介します。ここでは仮のデータに対してロジスティック回帰をする説明が掲載されています。
# データ読み込み
mydata <- read.csv("binary.csv")
mydata$rank <- factor(mydata$rank)
# ロジスティック回帰
mylogit <- glm(admit ~ gre + gpa + rank, data = mydata, family = "binomial")
# サマリーを見る
summary(mylogit)
# =>
# Call:
# glm(formula = admit ~ gre + gpa + rank, family = "binomial", data = mydata)
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -1.6268 -0.8662 -0.6388 1.1490 2.0790
# Coefficients:
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -3.989979 1.139951 -3.500 0.000465 ***
# gre 0.002264 0.001094 2.070 0.038465 *
# gpa 0.804038 0.331819 2.423 0.015388 *
# rank2 -0.675443 0.316490 -2.134 0.032829 *
# rank3 -1.340204 0.345306 -3.881 0.000104 ***
# rank4 -1.551464 0.417832 -3.713 0.000205 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# (Dispersion parameter for binomial family taken to be 1)
# Null deviance: 499.98 on 399 degrees of freedom
# Residual deviance: 458.52 on 394 degrees of freedom
# AIC: 470.52
# Number of Fisher Scoring iterations: 4
newdata1 <- with(mydata, data.frame(gre = mean(gre), gpa = mean(gpa), rank = factor(1:4)))
newdata1$rankP <- predict(mylogit, newdata = newdata1, type = "response")
newdata2 <- with(mydata, data.frame(gre = rep(seq(from = 200, to = 800, length.out = 100),
4), gpa = mean(gpa), rank = factor(rep(1:4, each = 100))))
newdata3 <- cbind(newdata2, predict(mylogit, newdata = newdata2, type = "link",
se = TRUE))
newdata3 <- within(newdata3, {
PredictedProb <- plogis(fit)
LL <- plogis(fit - (1.96 * se.fit))
UL <- plogis(fit + (1.96 * se.fit))
})
# グラフィックライブラリを使う
library("ggplot2")
ggplot(newdata3, aes(x = gre, y = PredictedProb)) + geom_ribbon(aes(ymin = LL,
ymax = UL, fill = rank), alpha = 0.2) + geom_line(aes(colour = rank),
size = 1)
# 結果を画像ファイルに落とす
ggsave("image.png")
まとめ
ひとまず今回はロジスティック回帰の概要と R で分析する例を紹介しました。ロジスティック回帰の話は次回に続きます。