PyTorch の社内勉強会の題材にしたいと思い立ち、畳み込みニューラルネットワーク(Convolutional Neural Network, CNN)を用いた自己対戦型強化学習の三目並べ AI を実装したので公開します。見通しの良いシンプルな実装を目指しました。結局、それなりのコード量になってしまいましたが。
動作環境
Google Colaboratory の CPUランタイムにて動作を確認しました。
概略
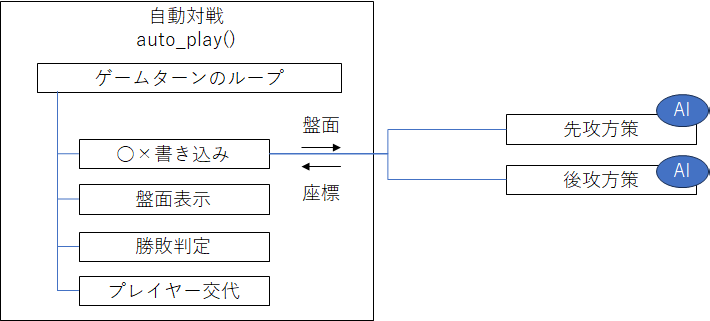
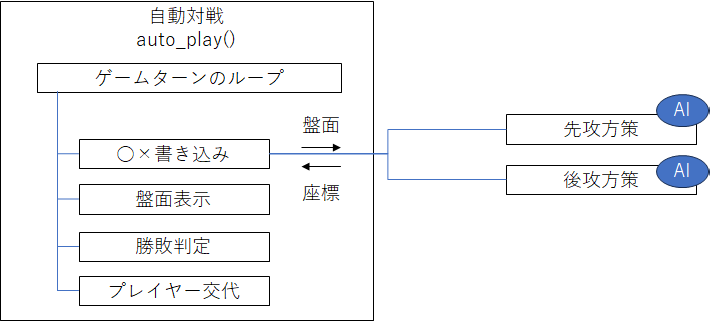
おおまかな処理フローは次図の通りです。盤面情報を受け取った先攻方策と後攻方策は、○×を書き込む場所を返します。この先攻方策と後攻方策に AI を実装し自己対戦させます。
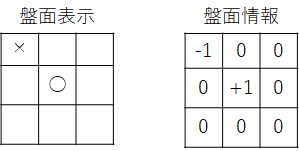
盤面情報は、空白マスをゼロ、先攻 ○ を+1、後攻 × を-1とした形状 (H,W)=(3,3) の二次元配列とします。
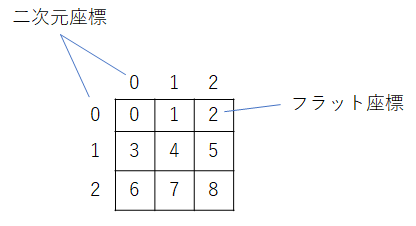
盤面座標は、場合により二次元座標と1次元に展開したフラット座標を使い分けます。
三目並べの実装
三目並べの土台となる機能は次の通りです。
- 盤面表示 plot()
- 勝敗判定 next_move()
- 自動対戦 auto_play()
- 方策乱択 policy_random()
- 自動対戦繰り返し repeat_play()
import time
import functools
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.nn.functional as F
DEVICE = 'cpu'
盤面表示 plot()
盤面表示は、盤面情報を Pandas の DataFrame 形式に変換し Notebook の組み込み関数 display関数にて表示、更新します。
def plot(board, handle=None, sleep_secs=0.8):
"""盤面表示"""
board = board.detach().cpu()
s_booard = np.zeros(board.shape, dtype='U') # 表示用の盤面作成
s_booard[board == +1] = '○' # 先攻(+1)の記号設定
s_booard[board == -1] = '×' # 後攻(-1)の記号設定
df = pd.DataFrame(s_booard.squeeze())
if handle is None:
handle = display(df, display_id=True) # 盤面初期表示
else:
handle.update(df) # 盤面更新
time.sleep(sleep_secs)
return handle
勝敗判定 next_move()
勝敗判定は、ゲームの勝敗を判定します。
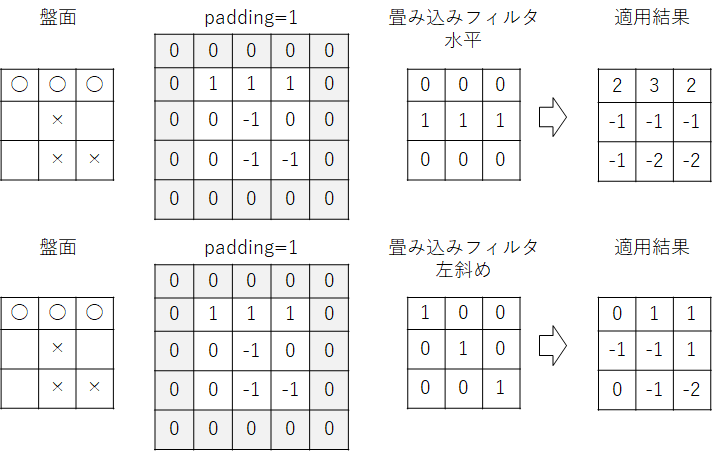
2次元畳み込み処理を用いて三目並びを検出するので、そのために必要な4つのフィルタ(水平、垂直、右斜め、左斜め)を準備します。
# 三目並びを検出するフィルタ. shape is (4,1,3,3)
FILTERS = torch.tensor([
# 水平
[[[0,0,0],
[1,1,1],
[0,0,0]]],
# 垂直
[[[0,1,0],
[0,1,0],
[0,1,0]]],
# 左斜め
[[[1,0,0],
[0,1,0],
[0,0,1]]],
# 右斜め
[[[0,0,1],
[0,1,0],
[1,0,0]]],
], dtype=torch.float32, device=DEVICE)
盤面情報とプレーヤー、次手のフラット座標を受け取り、次手の勝敗を判定します。
def next_move(board, player, nv, out=None):
"""次手 nv の勝敗を判定
Args
board : 現在の盤面. shape is (1,1,3,3)
player : +1 または -1
nv : 次手のフラット座標
out : 次手を格納する盤面. shape is (1,1,3,3)
Return
state : 勝者 +1 or -1. 引き分けまたは未定なら 0
"""
assert board.numel() == 9
assert player in (-1, +1)
assert nv in range(board.numel())
if board.flatten()[nv] != 0: # 空きマスでない場所に打つと相手の勝ち
return -player
out = board.detach().clone() if out is None else out
out.flatten()[nv] = player # 次手を入力
n_match = F.conv2d(out.view(1,1,3,3), FILTERS, stride=1, padding=1) # 並びの目数カウント
mask = n_match.abs() == 3 # 三目並びが成立している場所
state = n_match[mask].sign().sum().clamp(-1,1) # 勝者
return state.detach()
ここで F.conv2d() は PyTorch の二次元畳み込み処理です。畳み込みの結果 n_match は、形状が (N,F,H,W)=(1,4,3,3) の四次元配列となります。N はサンプル数、F はフィルタ数、H は高さ、W は幅です。
畳み込み処理を実行するとフィルタの数(F=4)だけ結果が作成されます。三目並びが成立しているマスの値は +3 または -3 となり、符号がプラスなら勝者は先攻、マイナスなら勝者は後攻です。
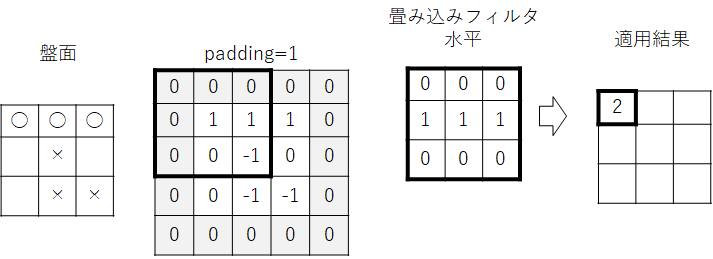
畳み込み処理の例
F.conv2d() の引数に padding=1 を指定しているのでまず盤面情報の周囲にゼロがパディングされます。その上で左上にフィルタを適用し要素と要素の積の総和を求めます。次図は、水平方向のフィルタを適用する場合の例です。
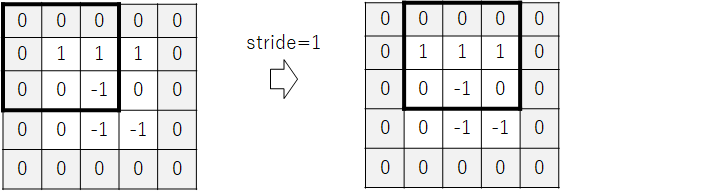
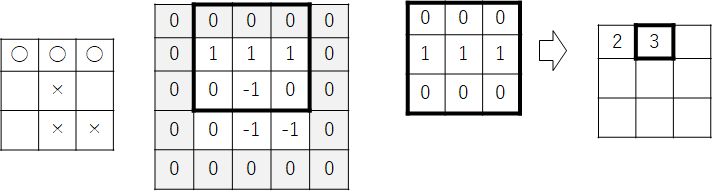
F.conv2d() の引数に stride=1 を指定しているのでフィルタの位置を1マス移動します。
同様に要素と要素の積の総和を求めます。次図の例では先攻の三目並びが成立しているので結果は3となります。
このようにフィルタの位置を移動しながら同様の処理を繰り返し、盤面の全てのマスについてフィルタの適用結果を求めます。次図上段は、水平方向のフィルタの適用結果、次図下段は、左斜め方向のフィルタの適用結果です。
自動対戦 auto_play()
自動対戦は、ゲームが終了するまでターンを繰り返します。関数の引数で外から方策 policies を与えられるようにします。
方策 policies は、先攻の方策が policies[0]、後攻の方策が policies[1] です。単一の方策が指定される場合があるため np.broadcast_to() で要素数が 2 の配列へブロードキャストします。
def auto_play(board, policies, display_handle=None):
"""自動対戦"""
policies = np.broadcast_to(policies, 2) # 先攻と後攻の方策
board[:] = 0 # 盤面リセット
if display_handle:
plot(board, display_handle) # 盤面表示
player = torch.tensor(1).float()
for turn in range(board.numel()): # ゲームターンのループ
bin = int(player == -1) # (-1,+1) to (1,0)
nv = policies[bin](board, player) # 次手を選択
state = next_move(board, player, nv, out=board) # 次手を打つ
if display_handle:
plot(board, display_handle) # 盤面表示を更新
if state != 0: # 勝敗が決したら終了
break
player = -player # プレーヤー交代
return state
方策乱択 policy_random()
方策乱択は、次手を打つ場所をランダムに決定します。
def policy_random(board, player):
"""方策乱択"""
blanks, = torch.where(board.flatten() == 0) # 空きマスを取得
nv = torch.randint(len(blanks), (1,)) # 空きマスから次手を乱択
return blanks[nv] # 盤面座標
以上のコードの動作を確認します。先攻と後攻の方策を「方策乱択」とし三目並べゲームを実行します。実行するとリアルタイムに盤面表示を更新する様子を確認できます。
def run():
"""自動対戦の動作確認"""
handle = display(None, display_id=True)
board = torch.zeros((3,3), dtype=torch.float32, device=DEVICE)
state = auto_play(board, policy_random, display_handle=handle)
msg = {-1: '×の勝ち', 0: '引き分け', 1: '○の勝ち'}
return msg[int(state)]
run()
自動対戦繰り返し repeat_play()
自動対戦繰り返しは、指定された回数の対戦を繰り返しその戦績を記録します。
def repeat_play(board, policy, N=100):
"""対戦をN回繰り返す
Return
counts : [後攻の勝ち数, 引分数, 先攻の勝ち数]
"""
states = [int(auto_play(board, policy)) for i in range(N)]
u, c = np.unique(states, return_counts=True)
assert set(u).issubset({-1, 0, 1})
counts = np.zeros(3, 'i')
counts[u+1] = c
return counts
自動対戦繰り返しの動作を確認します。
def run(N=100):
board = torch.zeros((3,3), dtype=torch.float32, device=DEVICE)
counts = repeat_play(board, policy_random, N=N)
with np.printoptions(precision=2, floatmode='fixed'):
print('[後攻 引分 先攻]')
print(counts / counts.sum(), '=', counts, '/', counts.sum())
run(N=1000)
実行結果
[後攻 引分 先攻]
[0.29 0.14 0.57] = [286 144 570] / 1000
1000回対戦すると先攻の勝率は 57%、後攻の勝率は 29% となりました。先攻が有利なようです。
三目並べの土台となる機能は以上です。
AI の実装
次は AI を実装します。
- 方策AI policy_ai()
- 方策AI学習 policy_train()
- 訓練
方策 AI policy_ai()
方策AIは、学習済みの AI を用いて次手を推論します。
def estimate(net, board, player):
"""AI推論"""
board = player * board # アクティブプレーヤを+1に強制
board = board.view(1, 1, *board.size()) # 形状を (N,C,H,W)=(1,1,3,3) に変更
return net(board).flatten() # 推論
def policy_ai(board, player, net=None):
"""AI方策"""
net.eval()
with torch.no_grad():
blanks, = torch.where(board.flatten() == 0) # 空きマスを取得
Q = estimate(net, board, player) # 次手の行動価値推定
action = blanks[Q[blanks].argmax()] # 価値最大の行動を選択
return action
ここで estimate() は 畳み込みニューラルネットワーク(以後、CNN)を実行し推論結果を返します。CNN への入力の形状は (N,C,H,W)=(1,1,3,3) です。N はサンプル、C はチャネル、H は高さ、W は幅。盤面情報は先攻が+1、後攻が-1 なので手番を +1 に強制します。
CNN の推論結果 $Q$ は、盤面9マスそれぞれについての行動価値です。行動価値を簡単にいうとそのマスを選択したときゲームに勝つ度合いです。上記のコードは、空きマスの中で行動価値 $Q$ が最大の手、つまりもっとも勝てそうなマスを選択しています。
なお、空きマス以外には打ってはいけないという禁則も含めて AI に学習させることもできますが、今回はコードで規制します。
方策 AI学習 policy_train()
三目並べで何らかの手を打ち最終的に勝ったとします。その場合、打った手が勝つ度合いを少し高くします。逆に負けた場合は、勝つ度合いを少し低くします。それを繰り返すと最終的に勝てる度合いが高い手と低い手が分かるようになります。
そのためには、ゲームが終了するまで分からない勝敗を、前の手に遡って学習させる必要がありそこがこの学習の難しい所です。
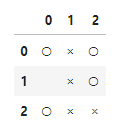
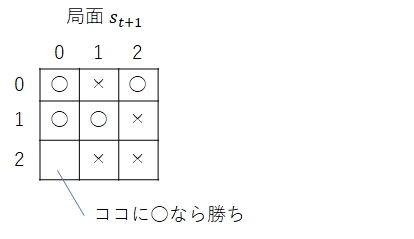
次図の局面 $s_{t+1}$ においてマス(2,0)に ○ を打つと ○ の勝ちが確定します。
このマス(2,0)を選択したときに得られる報酬 $r_{t+1}$ を勝ち点 $+1$ とします。なお、もし引分もしくはゲーム続行なら $0$、負けなら $-1$ とします。
r_{t+1} =
\begin{cases}
+1, & \mbox{if win} \\
0, & \mbox{if draw or unknown} \\
-1, & \mbox{if lose}
\end{cases}
局面 $s_{t+1}$ で選択した手を $a_{t+1}$ と表しその行動価値を $Q(s_{t+1}, a_{t+1})$ とすると AI の学習は、AI が推論する行動価値 $Q(s_{t+1}, a_{t+1})$ を報酬 $r_{t+1}$ に近づけるように学習します。
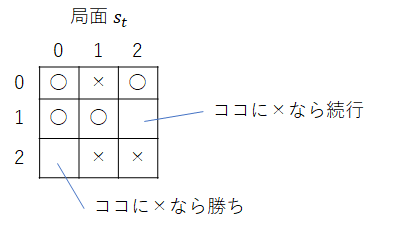
次に1つ前の局面 $s_{t}$ を考えます(次図)。マス(2,0)に × を打つと × の勝ちが確定し、マス(1,2)に × を打つと勝敗未定でゲーム続行です。
先ほどと同様にマス(2,0)を選択したとき得られる報酬を勝ち点 $+1$ とします。他方マス(1,2)を選択した場合、勝敗未定のため報酬は未定です。その場合は、局面 $s_{t}$ の行動価値 $Q(s_{t}, a_{t})$ を次局面 $s_{t+1}$ の行動価値 $Q(s_{t+1}, a_{t+1})$ に近づけるように AI を学習します。
以上からゲーム終了なら報酬 $r_t$ を、ゲーム続行なら次局面の行動価値 $Q(s_{t+1}, a_{t+1})$ を行動価値のターゲット値とします。行動価値のターゲット値 $Q'$ を次式のように定義します。
$$
Q'(s_t,a_t) = r_t - \gamma \max_{a_{t+1}}Q(s_{t+1}, a_{t+1})
$$
ここで $\gamma$(ガンマ)は伝搬の度合いを調整するハイパーパラメータです。
次局面 $s_{t+1}$ において対戦相手は取り得る手から最善手を選択するという仮定のもと次局面の行動価値の最大値をとります。また、対戦相手の最善手は自身にとっての最悪手という意味で符号を反転します。
def policy_train(board, player, net=None, optimizer=None, epsilon=0.5, gamma=1., report=None):
"""AIの学習"""
######################
# 行動価値の推定値
######################
net.train()
optimizer.zero_grad()
Q = estimate(net, board, player) # 行動価値推定
blanks, = torch.where(board.flatten() == 0) # 空きマスを取得
if torch.rand((1,)) < epsilon:
i = torch.randint(len(blanks), (1,)) # 空きマスから次手を乱択
action = blanks[i.item()]
else:
action = blanks[Q[blanks].argmax()] # 空きマスから価値最大の手を選択
Q_action = Q[action] # 次手 action の価値
######################
# 行動価値のターゲット値
######################
net.eval()
with torch.no_grad():
post = board.detach().clone()
state = next_move(board, player, action, out=post) # 次手の勝敗判定
blanks_next, = torch.where(post.flatten() == 0) # 次手の空きマスを取得
reward, Q_next = 0, 0
if state == player: # player の勝ち
reward = 1
elif state == -player: # player の負け
reward = -1
elif len(blanks_next) == 0: # 引き分け
reward = 0
else: # 勝敗未定
Q = estimate(net, post, -player) # 次々手の行動価値推定
Q_next = Q[blanks_next].max() # 相手にとって価値最大の行動を選択
Q_target = reward - gamma * Q_next
Q_target = torch.as_tensor(Q_target, dtype=torch.float32, device=Q_action.device)
######################
# パラメータ更新
######################
net.train()
loss = F.mse_loss(Q_action, Q_target)
loss.backward()
optimizer.step()
if report is not None:
report['loss'] += loss.item()
return action
訓練
では、自己対戦で AI を学習させてみましょう!ネットワークは CNN を用います。が、実質ニューラルネットワークです。ストライドがゼロなので。なお、学習中の進捗が分かるように方策乱択と対戦させます。
def run(n_episode=10000, interval=500, lr=0.01, N=100):
# ニューラルネットワーク
dim = 128
cnn = nn.Sequential(
nn.Conv2d(1, dim, kernel_size=3, padding=0, bias=False),
nn.Flatten(),
nn.Linear(dim, dim, bias=True),
nn.ReLU(True),
nn.Linear(dim, dim, bias=True),
nn.ReLU(True),
nn.Linear(dim, 3*3, bias=True),
nn.Tanh(),
).to(DEVICE)
# 評価時の方策
ai_vs_random = (
functools.partial(policy_ai, net=cnn),
policy_random,
)
random_vs_ai = (
policy_random,
functools.partial(policy_ai, net=cnn),
)
# 学習時の方策
op = torch.optim.SGD(cnn.parameters(), lr=lr)
rp = {'loss': 0.}
policy = functools.partial(policy_train, net=cnn, optimizer=op, report=rp)
print('# [後攻 引分 先攻]')
n_train = np.array([0,0,0])
board = torch.zeros((3,3), dtype=torch.float32, device=DEVICE)
start_tm = time.time()
for i in range(n_episode):
winner = int(auto_play(board, policy))
n_train[winner+1] += 1
if i==0 or (i+1) % interval == 0 or i+1 == n_episode:
n_1st = repeat_play(board, ai_vs_random, N=N)
n_2nd = repeat_play(board, random_vs_ai, N=N)
loss = rp['loss']
current_tm = time.time()
with np.printoptions(formatter={'float': '{:02.0f}'.format}):
print('[{}/{}] loss:{:.3f} %Train:{} %1st:{} %2nd:{} {:.3f}s'.format(
i+1, n_episode, loss,
100 * n_train / n_train.sum(),
100 * n_1st / n_1st.sum(),
100 * n_2nd / n_2nd.sum(),
current_tm - start_tm,
))
n_train[:] = 0
rp['loss'] = 0
start_tm = current_tm
return cnn
cnn = run(n_episode=10000, interval=500, lr=0.01, N=100)
実行結果
# [後攻 引分 先攻]
[1/10000] loss:0.989 %Train:[00 00 100] %1st:[40 20 40] %2nd:[21 20 59] 0.415s
[500/10000] loss:434.160 %Train:[31 04 64] %1st:[04 02 94] %2nd:[71 00 29] 4.090s
[1000/10000] loss:341.158 %Train:[27 05 68] %1st:[03 00 97] %2nd:[91 01 08] 3.918s
[1500/10000] loss:308.984 %Train:[27 06 67] %1st:[02 01 97] %2nd:[87 02 11] 3.838s
[2000/10000] loss:308.549 %Train:[31 06 63] %1st:[01 03 96] %2nd:[86 02 12] 3.990s
[2500/10000] loss:313.283 %Train:[30 06 65] %1st:[00 01 99] %2nd:[86 08 06] 3.996s
[3000/10000] loss:281.720 %Train:[28 09 63] %1st:[00 03 97] %2nd:[88 05 07] 3.974s
[3500/10000] loss:253.936 %Train:[24 09 67] %1st:[00 02 98] %2nd:[90 06 04] 3.986s
[4000/10000] loss:239.513 %Train:[28 11 61] %1st:[00 05 95] %2nd:[92 05 03] 4.048s
[4500/10000] loss:193.607 %Train:[26 15 59] %1st:[00 02 98] %2nd:[85 08 07] 4.031s
[5000/10000] loss:185.917 %Train:[26 10 64] %1st:[00 02 98] %2nd:[92 06 02] 4.004s
[5500/10000] loss:191.072 %Train:[22 15 63] %1st:[00 00 100] %2nd:[91 09 00] 4.117s
[6000/10000] loss:177.086 %Train:[23 15 62] %1st:[00 00 100] %2nd:[92 07 01] 4.115s
[6500/10000] loss:183.107 %Train:[21 21 59] %1st:[00 01 99] %2nd:[88 11 01] 4.199s
[7000/10000] loss:161.996 %Train:[23 21 56] %1st:[00 01 99] %2nd:[85 15 00] 4.209s
[7500/10000] loss:171.084 %Train:[20 24 56] %1st:[00 03 97] %2nd:[87 09 04] 4.316s
[8000/10000] loss:153.576 %Train:[24 20 56] %1st:[00 00 100] %2nd:[81 16 03] 4.202s
[8500/10000] loss:143.402 %Train:[21 26 53] %1st:[00 00 100] %2nd:[88 11 01] 4.362s
[9000/10000] loss:142.132 %Train:[24 23 53] %1st:[00 00 100] %2nd:[89 10 01] 4.314s
[9500/10000] loss:132.149 %Train:[24 23 53] %1st:[00 00 100] %2nd:[94 06 00] 4.319s
[10000/10000] loss:129.110 %Train:[21 25 53] %1st:[00 01 99] %2nd:[91 08 01] 4.333s
ここで %1st は、先攻をAI、後攻を乱択とした対戦を100回行った場合の勝率です。[後攻の勝率、引分、先攻の勝率]です。%2nd は先攻が乱択、後攻がAIです。後攻AIの学習の進み具合が今一つです。
学習後に今度はAIと乱択を1000回対戦させてみます。
先攻AI、後攻乱択の場合
def run(net):
"""先攻AI"""
policy = (
functools.partial(policy_ai, net=net),
policy_random,
)
board = torch.zeros((3,3), dtype=torch.float32, device=DEVICE)
n_test = repeat_play(board, policy, N=1000)
with np.printoptions(precision=3, floatmode='fixed'):
print('[後攻 引分 先攻AI]')
print(n_test / n_test.sum(), '=', n_test, '/', n_test.sum())
run(cnn)
実行結果
[後攻 引分 先攻AI]
[0.000 0.021 0.979] = [ 0 21 979] / 1000
先攻乱択、後攻AIの場合
def run(net):
"""後攻AI"""
policy = (
policy_random,
functools.partial(policy_ai, net=net),
)
board = torch.zeros((3,3), dtype=torch.float32, device=DEVICE)
n_test = repeat_play(board, policy, N=1000)
with np.printoptions(precision=3, floatmode='fixed'):
print('[後攻AI 引分 先攻]')
print(n_test / n_test.sum(), '=', n_test, '/', n_test.sum())
run(cnn)
実行結果
[後攻AI 引分 先攻]
[0.881 0.113 0.006] = [881 113 6] / 1000
やはり後攻AIとした場合の戦績が伸び悩んでいますが、時間切れのため今回はここまでとします。最後に先の説明で用いた局面 $s_t$ と $s_{t+1}$ の行動価値を期待通り推定できているか確認します。
行動価値の推定結果
局面 $s_t$
def run(net):
"""行動価値の動作確認"""
board = torch.tensor([
[1,-1,1],
[1,1,0,],
[0,-1,-1],
], dtype=torch.float32, device=DEVICE)
Q = estimate(net, board, -1).detach().cpu()
df = pd.DataFrame(Q.view(3,3))
with pd.option_context('display.float_format', '{:.2f}'.format):
display(df)
run(cnn)
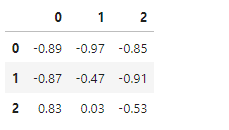
勝ちが確定するマス(2,0)の行動価値は 0.83 と高く、次局面で負けが確定しているマス(1,2)の行動価値は -0.91 と低くなっています。期待通りに学習できているようです。
局面 $s_t$
def run(net):
"""行動価値の動作確認"""
board = torch.tensor([
[1,-1,1],
[1,1,-1,],
[0,-1,-1],
], dtype=torch.float32, device=DEVICE)
Q = estimate(net, board, +1).detach().cpu()
df = pd.DataFrame(Q.view(3,3))
with pd.option_context('display.float_format', '{:.2f}'.format):
display(df)
run(cnn)
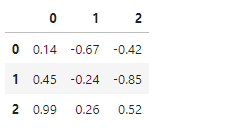
勝ちが確定するマス(2,0)の行動価値は 0.99 と高くなっています。こちらも期待通りです。
以上です。
ここまでお読みいただき、ありがとうございました。