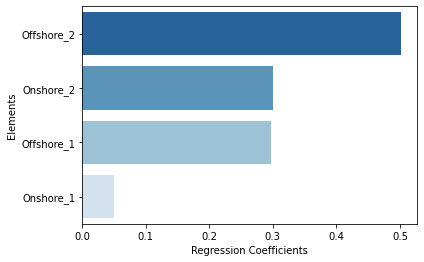やりたいこと
- 設備投資を行う際の建設コストのリスクを、モンテカルロ法を用いて定量化する
- 建設コストを構成する各要素の確率分布と相関関係を設定し、乱数組を生成する
設備投資を行う際、全体費用の大きな割合を占める建設コストは、天候・物価・人件費などの様々な要因によって大きく変動するという不確実性を有しています。
ここでは、建設コストを各要素に分解し、その確率分布と相関関係を設定したうえで、モンテカルロ法により建設コストの変動リスクを定量的に評価することを試みます。
モデル
簡単のため、建設工事は二つの洋上工事(Offshore_1,Offshore_2)および二つの陸上工事(Onshore_1,Onshore_2)によって構成されるものとし、建設コストはこれら個別のコストの合計と定義します。各工事コストのP10・最頻値・P90は以下の通り設定します。
| P10 | mode | P90 | |
|---|---|---|---|
| Offshore_1 | 100 | 250 | 400 |
| Offshore_2 | 300 | 350 | 800 |
| Onshore_1 | 900 | 925 | 950 |
| Onshore_2 | 300 | 550 | 600 |
また、各工事コストの相関関係は以下の通りとします。
(洋上工事同士・陸上工事同士はそれぞれ強い相関[0.9]があり、洋上⇔陸上間では弱い相関[0.5]があることをイメージしてモデル化しています)
| Offshore_1 | Offshore_2 | Onshore_1 | Onshore_2 | |
|---|---|---|---|---|
| Offshore_1 | 1.0 | 0.9 | 0.5 | 0.5 |
| Offshore_2 | 0.9 | 1.0 | 0.5 | 0.5 |
| Onshore_1 | 0.5 | 0.5 | 1.0 | 0.9 |
| Onshore_2 | 0.5 | 0.5 | 0.9 | 1.0 |
乱数生成
各要素の確率分布は三角分布に従うものとして、設定した入力条件を満足する乱数を生成します。
三角分布のクラスtriangular_fitはこちらのコードを使用しています。
また、乱数の生成方法について詳しくはこちらを参照してください。
import numpy as np
from triangular_dist import triangular_fit
from scipy.stats import norm,spearmanr,triang
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
# 試行回数
n = 50000
# 各要素の名前
name = ["Offshore_1","Offshore_2","Onshore_1","Onshore_2"]
# P10,最頻値、P90のリスト
elements = np.array([[100,250,400],
[300,350,800],
[900,925,950],
[300,550,600]])
# 各要素の相関関係
cor_coef = np.array([[1.0,0.9,0.5,0.5],
[0.9,1.0,0.5,0.5],
[0.5,0.5,1.0,0.9],
[0.5,0.5,0.9,1.0]])
# 三角分布の準備
tri_dists = []
for ele in elements:
#与えられたP10,mode,P90にフィットする三角形分布を生成
tri_dists.append(triangular_fit(ele[0],ele[1],ele[2]))
# 相関のある多変量正規分布の乱数z_listを生成
mu = np.zeros(elements.shape[0])
sigma = cor_coef
z_list = np.random.multivariate_normal(mu,sigma,n)
# 正規累積分布関数から、一様分布の乱数u_listを生成
u_list= norm.cdf(z_list)
# 逆関数法を用いてu_listから任意の分布を持つ乱数を生成
a_list = []
for i in range(u_list.shape[1]):
#三角分布に従う乱数を生成
a_list.append(tri_dists[i].ppf(u_list[:,i]))
a_list = np.transpose(a_list)
# DataFrameを生成
df = pd.DataFrame(a_list,columns=name)
# 生成した乱数のリストを出力
df
Offshore_1 Offshore_2 Onshore_1 Onshore_2 0 271.674899 423.619032 922.862146 436.283326 1 178.707851 354.904091 882.976324 217.474613 2 128.821805 403.111938 915.485525 448.719875 3 351.455486 734.054223 920.970889 521.520472 4 442.248604 903.573617 948.630335 551.485066 ... ... ... ... ... 49995 147.568593 395.741033 899.264791 331.173835 49996 382.085926 649.281076 912.453528 315.281751 49997 340.035343 627.800319 926.774642 458.619111 49998 187.235699 463.307672 917.633978 490.614796 49999 131.474132 387.047341 922.874209 449.360773 50000 rows × 4 columns
生成した乱数の可視化
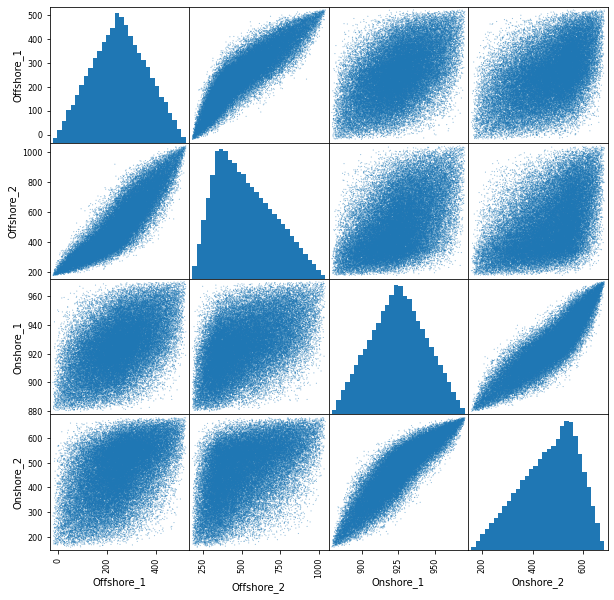
生成した乱数の散布図行列を出力してみます。
# 生成した乱数の散布図行列を出力 pd.plotting.scatter_matrix(df,figsize=(10, 10),hist_kwds={"bins":30},s=5) plt.show()対角成分は各変数のヒストグラム、それ以外は散布図を示しています。
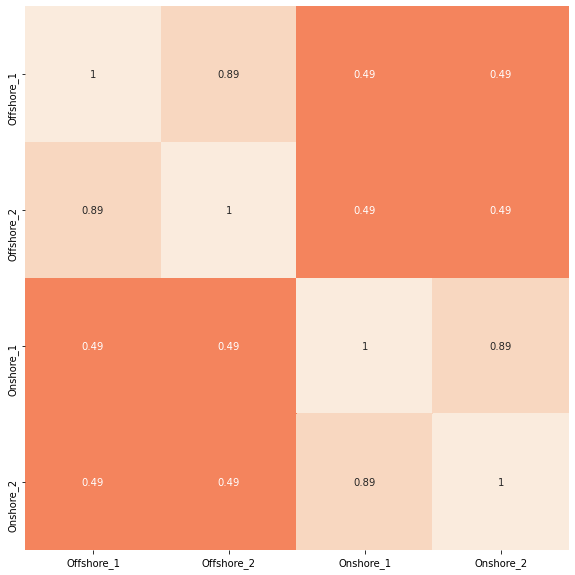
設定した入力条件を満足してそうですね。念のため相関係数も確認してみます。
# スピアマンの順位相関係数を算定、ヒートマップで出力 plt.figure(figsize=(10, 10)) sns.heatmap(df.corr(method='spearman'),vmax=1, vmin=-1,square=True, annot=True, cbar=False) plt.show()概ね入力条件で設定した相関関係の通りですね。
建設コストの算定
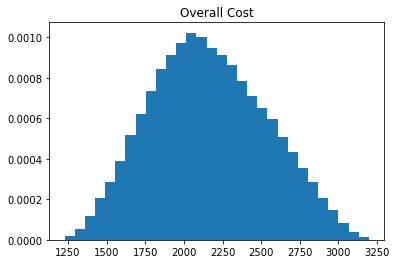
得られた乱数列の各行を足し合わせて、合計の建設コストを算定します。
# データフレームの各行の合計値を計算 sum_column = df.sum(axis=1) # 合計値のパーセンタイル値を計算 percentile = [10,25,50,75,90] df_percentile = pd.DataFrame(np.percentile(sum_column,percentile), index=["P10","P25","P50","P75","P90"], columns=["Overall Cost"]).T # ヒストグラムを出力 plt.hist(sum_column, bins=30, density=1) plt.title("Overall Cost") plt.show() # 合計値のパーセンタイル値を出力 df_percentile
P10 P25 P50 P75 P90 Overall Cost 1679.657667 1885.347016 2140.773801 2429.011128 2676.415322 これで合計の建設コストの分布を得る事ができました。
あとはリスク許容度に応じて、適切なパーセンタイル値を選択すればよさそうです。重回帰分析
得られた建設コストに対して、個別の要素がどの程度影響を及ぼしているのかを評価するため、
重回帰分析を行い標準偏回帰係数を比較します。重回帰分析にはscikit-learnを使用します。from sklearn import linear_model from scipy.stats import zscore # 重回帰分析モデルを作成 clf = linear_model.LinearRegression() # データフレームの各列を標準化 df_normalized=zscore(df, ddof=1) sum_normalized = zscore(sum_column, ddof=1) # 説明変数に標準化した各行のデータを使用 X = df_normalized # 目的変数に標準化した各行の合計値を使用 Y = sum_normalized # モデルにフィッティング clf.fit(X,Y) # 偏回帰係数を計算 df_reg_coef = pd.DataFrame({"Elements":df.columns, "Regression Coefficients":np.abs(clf.coef_)}).sort_values(by='Regression Coefficients', ascending=False) # 降順でグラフに描画 sns.barplot(x="Regression Coefficients",y="Elements",data=df_reg_coef,palette="Blues_r") plt.show() # 偏回帰係数を出力 df_reg_coef
Elements Regression Coefficients 1 Offshore_2 0.501799 3 Onshore_2 0.301040 0 Offshore_1 0.296749 2 Onshore_1 0.049565 今回のケースでは、全体の建設コストは、
- P10~P90の変動幅が最も大きいOffshore_2の影響を大きく受けている
- 一方で、絶対値は大きいものの変動幅が小さいOnshore_1の影響は相対的に小さい
ということが見て取れます。
最後に
今回のケースでは、建設コストは各要素の単純足し合わせとしましたが、例えば**[単価][数量]**といった要素を設定し、
[建設コスト]=[単価]×[数量]
とすれば、単価と数量の変動を考慮することも可能ですし、それらを組み合わせることで柔軟にモデルを構築可能です。
参考にしたサイト