やりたいこと
- 多変量正規分布に従う乱数を利用して、任意の確率分布に従う乱数を生成する
それぞれ任意の確率分布に従う乱数組が、相関関係を持つようにしたい場合の乱数の生成方法を紹介します。
SciPyを利用すれば、相関関係を持つ多変量正規分布に従う乱数を簡単に生成できるので、その乱数を利用して任意の確率分布に従うよう拡張します。
コード
import numpy as np
from scipy.stats import norm,spearmanr, expon
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
# 相関係数
cor_coef= 0.9
# 生成する乱数の数
n = 50000
# 相関のある多変量正規分布の乱数z_listを生成
mu = [0,0]
sigma = [[1,cor_coef],
[cor_coef,1]]
z_list = np.random.multivariate_normal(mu,sigma,n)
# 正規累積分布関数から、一様分布の乱数u_listを生成
u_list= norm.cdf(z_list)
# 逆関数法を用いてu_listから任意の分布を持つ乱数を生成
# ここでは1つは正規分布、もう一つは指数分布とする
a_list = [norm.ppf(u_list[:,0]),expon.ppf(u_list[:,1])]
a_list = np.transpose(a_list)
# DataFrameを作成
df = pd.DataFrame(a_list,columns=["x_normal","y_exponential"])
# スピアマンの順位相関係数を算定
r, p = spearmanr(df)
# ヒートマップ表示の散布図を出力
graph = sns.jointplot(x="x_normal",y="y_exponential",data=df, kind="hex")
phantom, = graph.ax_joint.plot([], [], linestyle="", alpha=0)
graph.ax_joint.legend([phantom],['spearman_r={:f}, p={:f}'.format(r,p)])
# DataFrameを出力
df
ここでは例として、一方は正規分布、もう一方は指数分布に従う乱数を生成します。
a_list = [norm.ppf(u_list[:,0]),expon.ppf(u_list[:,1])]
の部分を任意のPPF(Percent Point Function:累積分布関数の逆関数)に置き換えれば、任意の確率分布を表現できます。
出力
| x_normal | y_exponential | |
|---|---|---|
| 0 | -0.080616 | 0.916227 |
| 1 | -0.787544 | 0.461712 |
| 2 | -1.194595 | 0.190730 |
| 3 | 0.846426 | 1.149436 |
| 4 | 0.562191 | 1.813668 |
| ... | ... | ... |
| 49995 | 1.233940 | 2.735067 |
| 49996 | 0.003383 | 0.752736 |
| 49997 | 2.918661 | 3.950655 |
| 49998 | -0.123436 | 0.466713 |
| 49999 | 0.670042 | 1.349561 |
50000 rows × 2 columns
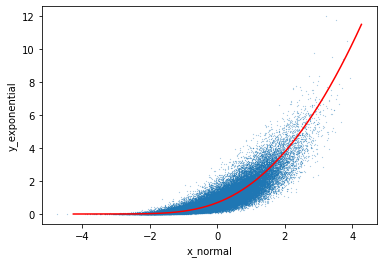
X軸は正規分布、Y軸は指数分布に従っていることが確認できます。相関係数も概ね設定した通りですね。
ここではスピアマンの順位相関係数を示しました。
二変数間の相関関係は非線形になるので、線形関係を評価するピアソンの相関係数で評価すると、期待しているよりも小さい値になる点には注意が必要です。
cor_coef→1のとき、散布図は下図の赤線に収束していきます。
x = np.arange(0,1,0.000001)
fig, ax = plt.subplots()
# 散布図
ax.scatter(df["x_normal"],df["y_exponential"],s=0.02)
# 累積分布がXのときの正規分布の値、指数分布の値を繋げた線
ax.plot(norm.ppf(x),expon.ppf(x),color='r')
ax.set_xlabel("x_normal")
ax.set_ylabel("y_exponential")
plt.show()
追記
ここでは2変数の場合について記載しましたが、多変数に拡張した応用例もありますので、よければ参照ください。
https://qiita.com/yasuyuki-s/items/0ec94fc879b9f0876cc2