はじめに
『すごいHaskellたのしく学ぼう(以下テキスト)』の14章8節に、カスタムモナドのサンプルとして「確率モナド」が載っている。今回は、この確率モナドを Scala の圏論ライブラリ Cats を用いて書いてみる。
また、テキストには「できたばかりのモナドが、きちんとモナド則を満たしているか試すことも、とても重要です。」との記述もある。これも大事なので、Discipline を使って確認してみる。
使用ライブラリ
compilerPlugin("org.spire-math" %% "kind-projector" % "0.9.8"),
"org.typelevel" %% "cats-core" % "1.6.0",
"org.typelevel" %% "cats-laws" % "1.6.0",
"org.scalacheck" %% "scalacheck" % "1.14.0",
"org.scalactic" %% "scalactic" % "3.0.5",
"org.scalatest" %% "scalatest" % "3.0.5" % "test",
データ型
テキストと同じように、型A の事象の離散確率分布を Prob[A] 型で表す。また、確率は Rational 型で表し、型A の例としてコインの裏表を表す Coin 型を定義する。以下、順に説明する。(ソース)
Prob
以下が Prob クラスで、型A の事象の離散確分布を、確率変数とその確率を組にした Event[A] のリストで表している。1
case class Prob[+A](es: List[Event[A]]) {
def map[B](f: A => B): Prob[B] = Prob(es.map { case (a, r) => f(a) -> r })
def flatMap[B](f: A => Prob[B]): Prob[B] = flatten(map(f))
}
object Prob {
type Event[+A] = (A, Rational)
def flatten[A](ppa: Prob[Prob[A]]): Prob[A] = Prob( for {
(pa, r1) <- ppa.es
(a, r2) <- pa.es
} yield a -> r1 * r2)
}
関数 flatten では、重なった Prob の外側の確率を内側の確率にかけてフラットにしている。これと map メソッドを合成すると flatMap になるが、後のカスタムモナド実装でこれを利用する。
Rational
確率を表す分数(有理数)のデータ型として、テキストでは Haskell のData.RatioのRationalを使っているが、ここでは自前でRationalを簡単に実装した。
case class Rational(n: Int, d: Int) {
def *(r: Rational) = Rational.apply(n * r.n, d * r.d)
}
object Rational {
def apply(n: Int, d: Int): Rational =
(n, d) foldMap (_ / gcd(n, d), new Rational(_, _))
private def gcd(a: Int, b: Int): Int = if (b == 0) a else gcd(b, a % b)
}
既約にできるものは、コンパニオンのapplyの時点で約分している(Rational(9, 15)→ Rational(3, 5)など)。ちなみに、refined を使えば分母を非ゼロとする制約を型レベルで表現することができるが、ここでは簡単のため省略した。
※ apply で使っている、(Int, Int) の foldMap については、記事の最後の方で補足した。
Coin
確率変数はなんでも良いが、テキストにならって裏・表を値に持つコイン型を採用し、sealed traitとcase object 用いた Sum Type で定義した。
sealed trait Coin
case object Heads extends Coin
case object Tails extends Coin
Haskellだとdata Coin = Heads | Tails deriving (Show, Eq)で済むが、Scalaの場合少し冗長になる。
モナドインスタンス
以下が「確率モナド」のインスタンス。(ソース)
object ProbInstances {
implicit def probMonad: Monad[Prob] = new Monad[Prob] {
def flatMap[A, B](pa: Prob[A])(f: A => Prob[B]): Prob[B] = pa flatMap f
def tailRecM[A, B](a: A)(f: A => Prob[Either[A, B]]): Prob[B] = {
val buf = List.newBuilder[(B, Rational)]
@tailrec def go(pes: List[(Prob[Either[A, B]], Rational)]): Unit = pes match {
case (Prob(e :: es), r0) :: tail => e match {
case (Right(b), r) => buf += (b -> r * r0) ; go(Prob(es) -> r0 :: tail)
case (Left(a2), r) => go(f(a2) -> r :: Prob(es) -> r :: tail)
}
case (Prob(Nil), _) :: tail => go(tail)
case Nil => ()
}
go(pure(f(a)).es)
Prob(buf.result)
}
override def pure[A](a: A): Prob[A] = Prob(List(a -> Rational(1, 1)))
}
}
ふつうモナドといえば $\eta: 1_C\rightarrow T$2 と$\mu: T^2\rightarrow T$3 に対応する関数だけ実装すれば良い気がするが、 Cats の Monad ではさらにtailRecMも実装する必要があり少しややこしい4。tailRecM 実装の中身の解説は割愛するが、cats-laws で tailRecM 周りのルールセットも提供されているので、後述の Discipline テストで確認できる。
REPLで動作確認
ここまでくると REPLから動かせる(コメントは後で追記したもの)。
scala> val coin = Prob(List((Heads, Rational(1, 2)), (Tails, Rational(1, 2))))
scala> val loadedCoin = Prob(List((Heads, Rational(1, 10)), (Tails, Rational(9, 10))))
scala> val result = for {
a <- coin // 公平なコイン
b <- coin // 公平なコイン
c <- loadedCoin // 1:9 に偏ったコイン
} yield List(a, b, c).forall(_ == Tails)
scala> result.es.foreach(println)
(false,Rational(1,40))
(false,Rational(9,40))
(false,Rational(1,40))
(false,Rational(9,40))
(false,Rational(1,40))
(false,Rational(9,40))
(false,Rational(1,40))
(true,Rational(9,40)) // 3つのコインが全て Tail になる確率は 9/40
本に載ってるghci上の動作と同じように動く。
テストコード
ベースとなるテストツールは ScalaTest を使った。以下のようなテストクラスで実行できる。(ソース)
class ProbMonadSpec extends FunSuite with Discipline {
implicit def defaultEq[A]: Eq[A] = (x, y) => x == y
implicit def genRational: Gen[Rational] = for {
n <- Gen.choose(-3, 3)
d <- Gen.choose(-3, 3).retryUntil(_ != 0)
} yield Rational.apply(n, d)
implicit def arbRational: Arbitrary[Rational] = Arbitrary(genRational)
implicit def genProb[A](implicit arb: Arbitrary[List[Event[A]]]): Gen[Prob[A]] =
arb.arbitrary.map(Prob(_))
implicit def arbProb[A](implicit arb: Arbitrary[A]): Arbitrary[Prob[A]] = Arbitrary(genProb[A])
implicit def genCoin: Gen[Coin] = Gen.oneOf[Coin](Heads, Tails)
implicit def cogenCoin: Cogen[Coin] = Cogen { _ match {
case Heads => 1L
case Tails => 0L
}}
implicit def arbCoin: Arbitrary[Coin] = Arbitrary(genCoin)
checkAll("Monad[Prob[Coin]]", MonadTests[Prob].monad[Coin, Coin, Coin])
}
最後のcheckAllでMonadTests#monadで定義されたルールが検証される。前提となる implicit は以下のとおり。
-
defaultEq: 期待値と実際値を比較するためのEq -
genRational/arbRational: 確率Rationalを表す分数の生成 -
genProb/arbProb: 確率分布Probを表す分数の生成 -
genCoin/cogenCoin/arbCoin: コインの生成
##実行結果
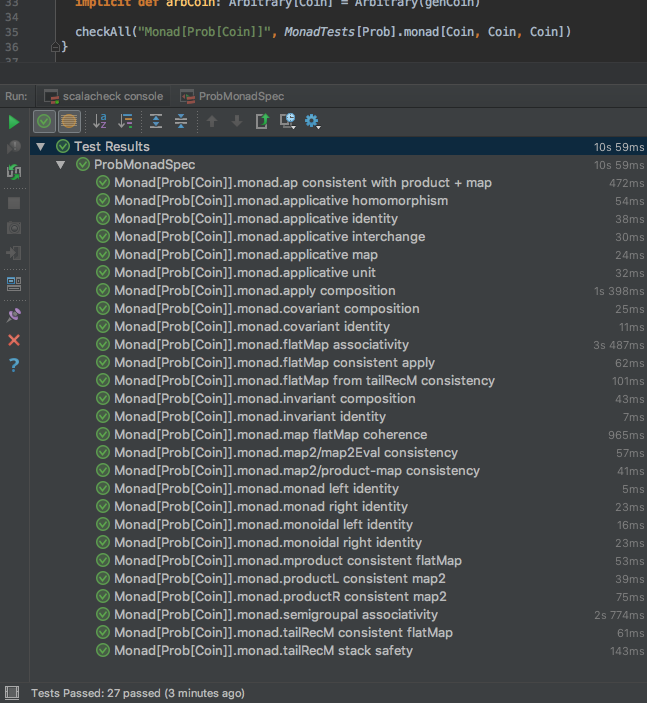
以下、IntelliJ からの実行のスクリーンショット。
27個もあるが、テキストに記載の3箇条のモナド則は、monad left identity、monad right identity、flatMap associativityあたりが対応。
上ですこし触れたとおりtailRecM の実装はけっこう難しいが、例えばスタックセーフになってなければ tailRecM stack safety でエラーになったり、あるいは内部の計算に矛盾があると tailRecM consistent flatMap や flatMap from tailRecM consistency でこけたり、ちゃんとテスト失敗するのでかえって安心感がある。
よく見ると11秒もかかっているが、テストケースのサイズを小さくできるかもしれない。ちなみにCoin型でなくIntなどでも正しく動く。
##所感
- cats-laws で提供されるルールセットの discipline テストは、暗黙に要求されている各種インスタンスが多いので、慣れるまではコンパイルを通すことからしてやや難しい。またコンパイルできてもテストコードが悪いのかテスト対象コードが悪いのかすぐには分かりにくく、はじめは苦労するかもしれない。
- ただし、一旦コンパイルが通って思い通りのテスト結果が得られるようになると、かなり安心感がある。
tailRecMの実装などはこれがないと逆に難しかった。
補足
同じ型の要素からなるタプル (A, A) に関数 f:A=>R を適用する、以下のような拡張メソッドを利用している(抽象度も高く一般的に使えるが、ここでは便宜上 object Rational に置いた)。
implicit class PairOps[A](val t: (A, A)) extends AnyVal {
def map[R](f: A => R): (R, R) = (f(t._1), f(t._2))
def foldMap[R, B](f: A => R, g: (R, R) => B): B = g.tupled(t map f)
}
REPLでの挙動。
scala> (1, 2) map (_ + 10)
res0: (Int, Int) = (11,12)
scala> (1, 2) foldMap[Int, Int] (_ * 10, _ + _)
res2: Int = 30
map で分かるように、同じ型の組は関手になるし、さらに表現可能関手にもなる。