Cats の表現可能関手
圏論の表現可能関手が Scala の関数型プログラミングライブラリ Cats にもあるので調べてみた。
はじめに
前の投稿では、ふだんあまり使わないけど何か興味を惹かれる、Cats の型クラスについて調べてみた。今回も同じような趣旨で、表現可能関手 という圏論の概念の Cats 実装、Representable を調べてみたい。
自分の圏論レベルは、最近やっと米田の補題を自力で証明できるようなって、「随伴は至るところに見られる」というあたりを勉強中のまだ入門段階あたり。ただし、プログラマー的にキャッチーなトピックについては、純粋な圏論の学習とは別に以前からつまみ食いしていて、モナドの可換図を書いたり、モノイドの圏の絵を書いて説明する程度なら何となくできる感じ。
使っている教科書は、『ベーシック圏論』 で、Awodey 本1 でもやや難しく感じる自分でも読めるレベルのもの。モナドは載ってないけど、そのぶん基本概念の説明が親切で、構成もわかりやすくて読みやすい。以下、表現可能関手の定義なども、このテキストから引用する。
また教科書で知ったことではないが、Cats の実装では Representable からの Monad や Bimonad の導出も提供されていて、これも面白いので紹介したい。
表現可能関手の概要
『ベーシック圏論』では、普遍性 への3つのアプローチとして、「圏の間の関係」についての随伴、「圏の内部で起こること」についての極限、「集合値関手の性質」についての表現可能性を、構成の柱としている。とくに表現可能関手は3つめの「集合値関手の性質」にまつわるトピックで、米田埋め込みや米田の補題につながる入り口にもなっている。
表現可能関手というくらいだから、まず表現というなんらかの概念があって、ある種の関手にはそれが可能になることが字面からも想像できるが、以下それぞれテキストをひも解いて個別に見てみる。
表現可能であるとは?
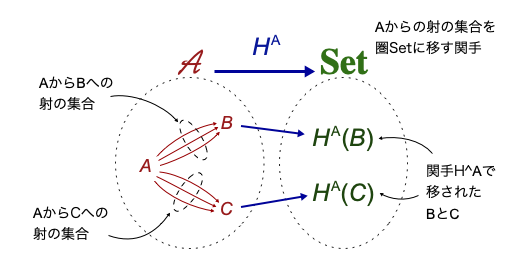
テキストには「関手 $X: \mathscr{A} \rightarrow \mathbf{Set}$ が表現可能(representable)であるとは、ある $A ∈ \mathscr{A}$ について、$X ≅ H^A$ となることをいう。」とされている。ここで $\mathbf{Set}$ とは、対象が集合で射が集合間の写像であるような圏、また $\mathscr{A}$ は 2つの対象の間の射の集まりが集合になるような圏(ざっくり普通の圏)になる。
$H^A$ は、値域が $\mathbf{Set}$ となる集合値関手の一種で、$\mathscr{A}$ のある要素を、同じく$\mathscr{A}$ の要素 $A$ からそこに向かう射の集合2( $\mathbf{Set}$ の要素)に移すものになる。($H^A$ の他に $\mathbf{Hom}(A, -)$ のような記法もある。)
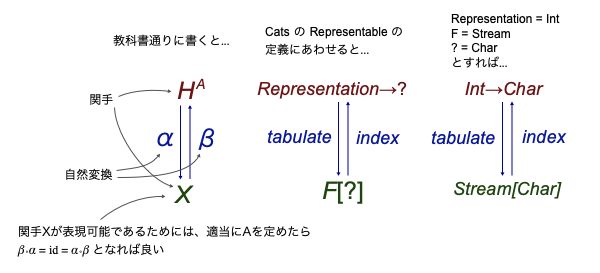
この $H^A$ が関手 $X$ と同型、つまり $X ≅ H^A$ であるとは、自然変換 $\alpha: H^A \rightarrow X$ と $\beta: X \rightarrow H^A$ があって、$\beta \circ \alpha = id_{H^A}$ かつ $\alpha \circ \beta = id_{X}$ になることを言う。
ちなみに表現「可能」というからには、表現が不可能な関手もあるが、それは後述する。
表現とは?
これもテキストから引用すると、「$X$ の表現(representation)とは、対象 $A ∈ \mathscr{A}$ と $X ≅ H^A$ の選択である。」とされている。つまり Scala プログラミング的に言い換えると、型 $A$ に何を選んで、2つの関数 $X \rightarrow H^A$ と $H^A\rightarrow X$ をどう実装するかが、Functor $X$ の表現ということになる。
ここから先は Scala + Cats で考えてみる。
Catsでは
Cats の Representable を簡素化して引用すると以下のようになっている。
trait Representable[F[_]]:
def F: Functor[F]
type Representation
def index[T](f: F[T]): Representation => T
def tabulate[T](f: Representation => T): F[T]
これを上の圏論的な表現可能関手の定義と対応させると以下のようになる。
| 圏論 | Cats の Representation |
|---|---|
| $A$ | Representation |
| $H^A$ |
Representation からなにかへの関数 |
| $X$ | F: Functor[F] |
| $\alpha: H^A \rightarrow X$ | tabulate[T]: (Representation=>T) => F[T] |
| $\beta: X \rightarrow H^A$ | index[T]: F[T] => (Representation=>T) |
ここで index をよく見るとわかるように、F[T] からなんらかの型 T の値が得られない場合には、結果とする関数が作れない。つまり、つねに必ずT値が得られる Functor[F] でないと index が定義できず、「表現可能」になりえないということになる。Scala + Cats 的には、こうした表現不可能な関手の中には、例えば Option や List などのような値が空のケースをもつデータ型があって、これらについては Representation インスタンスが作れない。
逆に表現可能なものには、例えば Tuple2[A, A]、NonEmptyList、無限長の LazyList などが含まれる。まとめて図示すると下のようになる。
これを踏まえて、LazyList と Tuple3[A, A, A] を例にとって実装してみる。
実装例
LazyList
まず上で例示した 無限長の LazyList を表現してみる。
given Representable.Aux[LazyList, Int] = new Representable[LazyList]:
type Representation = Int
def F: Functor[LazyList] = summon
def tabulate[A](f: Int => A): LazyList[A] = LazyList.from(0) map f
def index[A](f: LazyList[A]): Int => A = f.apply
Representation は Int3 とした。こうすると、自然変換 index は、与えられた LazyList から、位置→要素のマッピングを返すように、逆に tabulate は、位置→要素のマッピングから LazyList を返すように実装できる。これが LazyList の表現となる。
ざっと Scala Worksheet で動かした結果。
val index = LazyList.continually("abc".to(LazyList)).flatten.index
(5 until 10) map (n => s"$n:${ index(n) }") // Vector(5:c, 6:a, 7:b, 8:c, 9:a)
val tabulate = ((n: Int) => ('x' + (n % 3)).toChar).tabulate
tabulate.take(5).toList // List(x, y, z, x, y)
ちゃんと表現可能関手になっているか、Discipline で確認してみる。
class LazyListSuite extends DisciplineSuite:
val genNonNegative : Gen[Int] = Gen.chooseNum(0, 4)
val genChar : Gen[Char] = Gen.oneOf('a', 'b', 'c')
val genCharLazyList: Gen[LazyList[Char]] = Gen.listOfN(5, genChar).map(_.to(LazyList))
given Arbitrary[Int] = Arbitrary(genNonNegative)
given Arbitrary[LazyList[Char]] = Arbitrary(genCharLazyList)
given Eq[LazyList[Char]] = _.take(5) == _.take(5)
checkAll("Representablity of LazyList", RepresentableTests[LazyList, Int].representable[Char])
理論的には無限長の LazyList なのだけど、それだと比較もできないので、サンプルデータとしては文字 a、b、c のいずれかを要素として持つ最大長5までの LazyList とした。実行すると下記のように成功する。
representable_functor.LazyListSuite:
+ Representablity of LazyList: representable.index andThen tabulate = id 0.031s
+ Representablity of LazyList: representable.tabulate andThen index = id 0.01s
[info] Passed: Total 2, Failed 0, Errors 0, Passed 2
教科書的な記述に戻ると、$\beta \circ \alpha = id_{H^A}$ かつ $\alpha \circ \beta = id_{X}$ が確かめられたことになる。
Tuple3
Cats では (A, A) の Representable インスタンスも提供されているが、ここではちょっと変えて、Triple[A]=(A, A, A) で試してみる。
「表現」を実装する前に、まず関手として扱えるように準備しておく。
type Triple[A] = (A, A, A)
given Functor[Triple] with
def map[A, B](fa: Triple[A])(f: A => B): Triple[B] = (f(fa._1), f(fa._2), f(fa._3))
Cats の関手(A, A) の表現では Boolean を採用していたが、Triple の例では、負、ゼロ、正の整数に対応付けてみたい。
given Representable.Aux[Triple, Int] = new Representable[Triple]:
type Representation = Int
def F = Functor[Triple]
def index[A](f: Triple[A]): Int => A = n =>
if n < 0 then f._1
else if n > 0 then f._3
else f._2
def tabulate[A](f: Int => A): Triple[A] = F.map(-1, 0, 1)(f)
Scala Worksheet から実行すると以下のようになる。
type Sign = "minus" | "zero" | "plus"
val triple: Triple[Sign] = ("minus", "zero", "plus")
(-10 to 10 by 5) map triple.index
// res2 = Vector(minus, minus, zero, plus, plus)
val g = (n: Int) => if n < 0 then '-' else if n > 0 then '+' else '0'
g.tabulate[Triple]
// res3: Triple[Char] = (-,0,+)
g.tabulate[Triple].index.apply(10)
// res4: Char = +
これも Discipline で以下のようにテストしてみる。表現となる Int は -2 〜 2 の整数とし、tabulate に与える関数は、3種類用意して、ランダムに選ばれるようにした。
class TripleSpec extends DisciplineSuite:
given Apply[Gen] with
def ap[A, B](ff: Gen[A => B])(fa: Gen[A]): Gen[B] = ff flatMap fa.map
def map[A, B](fa: Gen[A])(f: A => B): Gen[B] = fa map f
given Arbitrary[Triple[Int]] = Arbitrary {
val smallInt = Gen.chooseNum(-2, 2)
(smallInt, smallInt, smallInt).mapN((_, _, _))
}
given Arbitrary[Int => Char] = Arbitrary {
Gen.oneOf((' ', ' ', ' '), ('a', 'b', 'c'), ('-', '0', '+')) map { case (x, y, z) =>
(n: Int) => if n < 0 then x else if n > 0 then y else z
}
}
checkAll("Representablity of Triple", RepresentableTests[Triple, Int].representable[Char])
LazyList と同様に自然同型の条件が満たされ、テストが成功する。
Monad と Bimonad
『ベーシック圏論』からの話題ではないが、Cats のソースに Representable から Monad と Bimonad を得る実装があった。ちょっと面白いので紹介する。
Monad
疑似コードで書くと下のようになる。Representable の index と tabulate から、Monad の pure と flatMap を導いている。
pure: A → FA =
a → tabulate(_ → a)
flatMap: FA → (A → FB) → FB =
fa → f → tabulate(r → index(f(index(fa)(r)))(r))
先に実装した Triple で試してみると、下記のようになる。
val monad = Representable.monad[Triple]
monad.pure('x')
// res7: Triple[Char] = (x,x,x)
monad.flatMap(('x', 'y', 'z'))(a => (s"1$a", s"2$a", s"3$a"))
// res8: Triple[String] = (1x,2y,3z)
Representable から Monad が得られた。ちょっと不思議で面白い。
Bimonad
Bimonad も同様に index と tabulate を組み合わせて、coflatMap と extract を導いている。ただし表現 Representation がモノイドであることが要求される。
coflatMap: FA → (FA→B) → FB =
fa → f → tabulate(r1 → f(tabulate(r2 → index(fa)(combine(r1, r2)))))
extract: FA → A =
fa → index(fa)(empty)
実行すると下記のようになる。
val monAdd = new Monoid[Int]:
def empty: Int = 0
def combine(x: Int, y: Int): Int = x + y
val monMul = new Monoid[Int]:
def empty: Int = 1
def combine(x: Int, y: Int): Int = x * y
val bmAdd = Representable.bimonad[Triple, Int](repr, monAdd)
val bmMul = Representable.bimonad[Triple, Int](repr, monMul)
bmAdd.extract(('x', 'y', 'z'))
bmMul.extract(('x', 'y', 'z'))
bmAdd.coflatMap(('x', 'y', 'z'))(t => s"$t") // ((x,x,y),(x,y,z),(y,z,z))
bmMul.coflatMap(('x', 'y', 'z'))(t => s"$t") // ((z,y,x),(y,y,y),(x,y,z))
coflatMap が特に興味深い。モノイドによって異なる結果になる。
バージョン -> Scala 3.1.3, cats: 2.8.x, scalaCheck: 1.16.x あたり (その他)
所感とメモ
- 「Haskell の数学的背景を知るのに良い方法は、Haskell 自体をよく勉強すること」とはよく聞くけど、Scala の Cats でやってみても意外な発見があったりして面白い。
- 圏論の本を読んでると、圏論的概念の例として、他の数学分野から持ってきた素材が使われることが多いけど、プログラマの場合は、圏論から影響を受けた言語やライブラリなどで具体的に確かめられる材料がわりと豊富で助かる。
- サンプルコードを Scala 3 ベースで書き直した (2022-07-26)