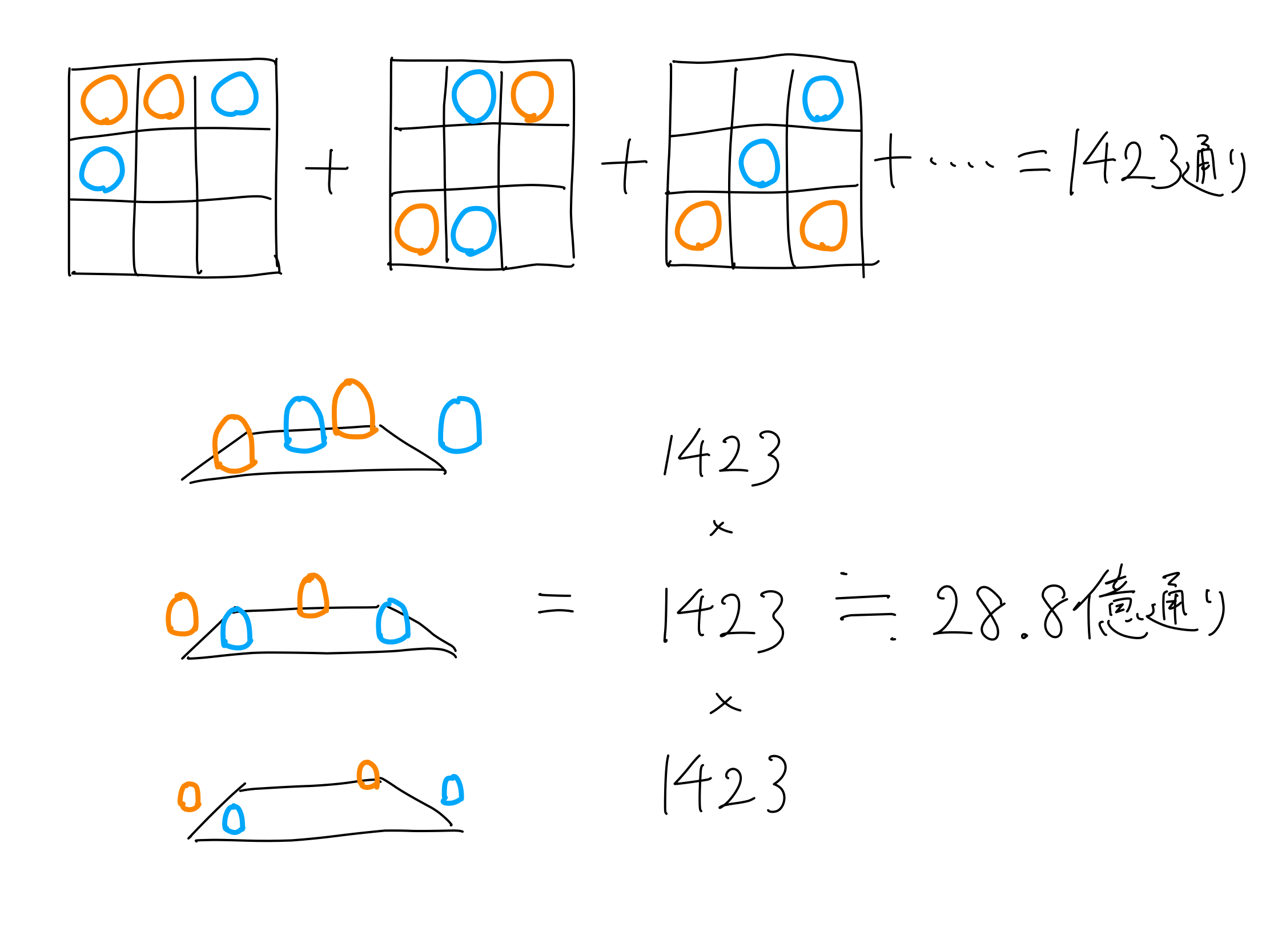はじめに
前回の記事で○×ゲームの必勝を判定するプログラムを作りました → 【Python】ミニマックス法を用いて○×ゲームの必勝を判定する
本記事ではゴブレットゴブラーズの完全解析を行うとともに、解析プログラムを作成する手順について公開する。更に今回の解析で発見した興味深い性質を掲載するので、ゴブレットゴブラーズを理解するのに役立てて欲しい。
ゴブレットゴブラーズとは
○×ゲームに少し複雑さを取り入れ、ゲーム性を高めたボードゲームである。→本家サイト
株式会社QuizKnockが紹介している動画がこちら → 進化した〇×ゲームが奥深すぎる【東大ボドゲ】
ルールについて簡潔な解説をする。詳しくは上記動画や制作元リンクを参照
一対一で対戦するボードゲームであり、二人はそれぞれ大中小3種類の駒が2つずつ(計6つ)の駒が与えられる。3x3のマス目のあるボードに交互に駒を置いていき、縦横斜めいずれかの一列が揃った方のプレイヤーが勝利となる。
また場に置いている駒より大きい駒であれば被せて置くことができ、既に場に置いてある駒を動かして異なるマスに再び置くこともできる。被せられている駒は動かせず、勝利条件に使うこともできない。
またルールには載っていないが便宜上、一回の対戦で同じ局面が二度出現した場合に千日手=引き分けとするという決まりを追加している。
概要
実行環境はPython3.8 Google ColabのJupyterNotebook(メモリ25.46GB)上で行った。
当初は前回の記事で使用したミニマックス法によって探索を行っていたがうまく行かず、調べたところ後退解析による解法が一般的らしかったのでこちらをメインのアルゴリズムとして採用した。
また持ち駒や千日手の概念があるという共通点から、どうぶつしょうぎの必勝解析を大いに参考にし実装を行った。
考察の手順
1.盤面数の考察
①一種類のコマしかない場合(ここでは自分の大の駒2つ+相手の大の駒2つのみの場合)について考える。
このとき自分の駒の置き方は、盤面上にある自分の駒の数を自然数$k$と置くと、${}_9C_k$と表せる。
更に盤面上にある相手の駒の数を自然数$l$と置くと、相手の駒を含めた置き方は
$${{}_9C_k} _{9-k}C_l = \frac{9!}{k!l!(9-k-l)!}$$
と表せる。このとき$k$, $l$は $0\leqq{k, l}\leqq2$ の範囲で値をとるので、場合の数は全部で
$$\sum_{k=0}^2\sum_{l=0}^2\frac{9!}{k!l!(9-k-l)!}$$
となり、これを計算すると$1423$となる。よって、一種類の駒のみの場合1,423通りの置き方があることがわかった。
②1の結果を用いて全てのコマがある場合について考える。
少し考えてみると、ある種類のコマの配置は違う種類の駒の配置に依存しないことがわかる。
例えば小さい駒と大きい駒が同じマスに配置されるとき、小さい駒に大きい駒が被せてあると考えることができるため、重複の問題が発生しない。よって異なる種類の駒はそれぞれ独立していると考えることができる。
したがって盤面の総数は$1423^3$=2,881,473,967通りと考えることができる。
また、本来であればこれに先手後手の情報が加わるため盤面の総数*2が全状態数となるが、後手の局面というのは敵味方の駒を全て入れ替えた先手の局面として扱うことができるため、考慮する必要がない。(これは前回の記事では気づけなかった反省点である)
ここで求めたものは局面の番号付けに使う。局面数だけの長さの配列を作り、局面に一対一で対応する番号に評価値を格納していく。これにより各局面での勝敗を記録していく。
※注意すべき点としてこれはあくまで場合の数の最大に過ぎず、実際には対称な局面や到達し得ない局面が含まれているため、探索が必要な局面数は計算結果より少なくなると考えられる。
しかしこれらを除いた局面数を求めるにはより高度な数学的考察が必要となり、更に28億程度であれば配列を作成するためのメモリを十分確保することができたため、これ以上は工夫せず$1423^3$通りとして考察をすすめる。
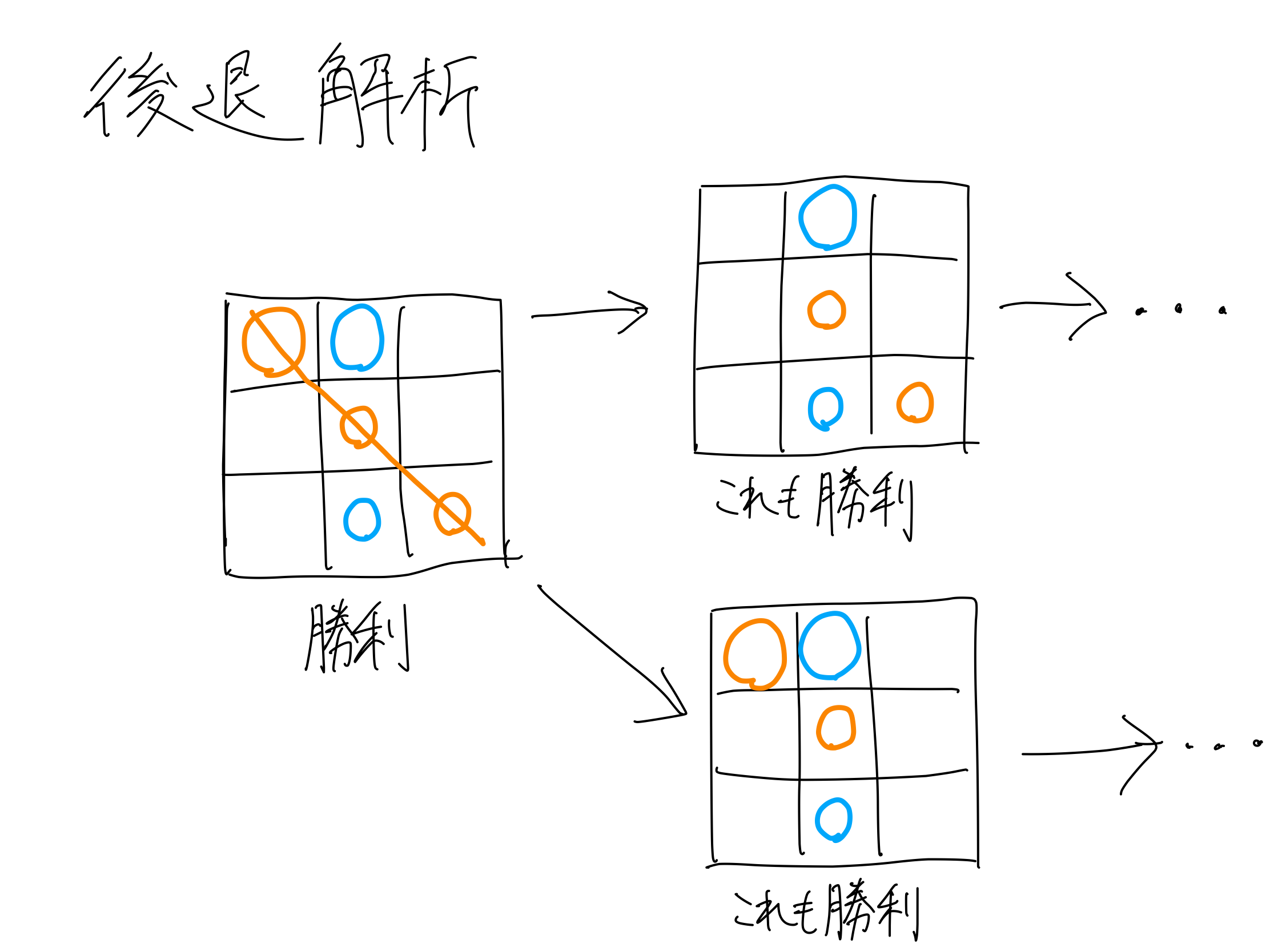
2.後退解析を用いて局面の勝ち負けを確定していく
こちらの論文を参考にして実装を行った。
*( 1 )勝負のついた局面の集合から開始する.
( 2 )勝負のついた局面の1手前の局面を求める.
•(手番のプレイヤーの)負け局面から1手前の局面は(手番のプレイヤーの)勝ち局面
•勝ち局面から1手前の局面の勝敗が未確定の時は,そこから可能な手がすべて勝ち局面に移行する時は,負け局面とする.
( 3 )操作を繰り返して,勝ち局面の集合も負け局面の集合がそれ以上増えなくなったら終了する.
こちらの文献を参考にさせて頂きながら、以下のような手順で後退解析を行った。
-
まず勝負のついた局面の集合は、先ほど求めた$1423^3$全ての局面について終了局面かどうかの判定を行うことで求める。また勝敗が確定した局面に対称な局面があれば同時に確定させ、探索回数を減らす。
この条件で計算した結果、終了局面は644,016,624通りと求められた。 -
次に1で求めた終了局面の集合からBFS(幅優先探索)を行うことにより、1手前の局面を求めていく。
ここでの注意点として、他の駒に隠れている駒は動かせないということと、持ち上げた瞬間に相手の駒が一列揃ってしまうような駒は持ち上げた瞬間負け=動かせないということに気をつける。 -
操作を繰り返して,勝ち局面の集合も負け局面の集合がそれ以上増えなくなったら終了する。
解析結果
終了局面の探索に約6.8時間、すべての局面の勝敗を求めるのに約1日を費やした結果、先手必勝であることがわかった。初手局面から両者が最善手を指し続けた場合、13手で先手が勝利する。
3. 解析結果の検討
各局面の終了局面までの局面数
それぞれの局面を開始局面として、先手後手が最善手を指し続けた場合に終了局面までかかる手数を求めた。結果、このような内訳となった。
なお、この局面の中には初手局面から到達できないものも含まれている。また明らかに終了局面を過ぎているような局面は「到達不可能」として除外してある。
| 終了局面までの手数 | 総局面数 |
|---|---|
| 0(終了局面) | 644,016,624 |
| 1 | 1,228,663,244 |
| 2 | 121,570,146 |
| 3 | 59,679,998 |
| 4 | 31,619,662 |
| 5 | 18,065,938 |
| 6 | 10,012,296 |
| 7 | 6,323,572 |
| 8 | 3,359,624 |
| 9 | 2,174,189 |
| 10 | 1,030,263 |
| 11 | 630,495 |
| 12 | 298,247 |
| 13(初手局面含む) | 178,654 |
| 14 | 86,783 |
| 15 | 50,854 |
| 16 | 30,888 |
| 17 | 15,672 |
| 18 | 10,412 |
| 19 | 6,396 |
| 20 | 4,220 |
| 21 | 2,004 |
| 22 | 1,852 |
| 23 | 1,244 |
| 24 | 688 |
| 25 | 328 |
| 26(最大) | 76 |
| 到達不可能 | 752,732,880 |
| 合計 | 2,880,567,249 |
※千日手の局面を含まない
また勝ち負けでの分類はこの通りとなる。
| 勝ち局面 | 1,315,792,588 |
| 負け局面 | 812,041,781 |
| 千日手局面 | 906,718 |
| 合計 | 2,128,741,087 |
※到達不可能な局面の数を含まない
最序盤考察
まずは初手の解析を行う。初手として取りうる手と終局までの手数を一覧にして出力した結果が以下である。駒の表現は▫=小、□=中、◇=大の駒としてそれぞれ表現している。(count = 終局までの手数)
wins=18, draws=0, loses=9
wins:
count = 12
--- ▫-- ---
--- --- ---
--- --- ---
count = 12
◇-- --- ---
--- --- ---
--- --- ---
count = 12
--- --- ---
--- ◇-- ---
--- --- ---
count = 14
▫-- --- ---
--- --- ---
--- --- ---
count = 14
--- --- ---
--- ▫-- ---
--- --- ---
count = 14
--- ◇-- ---
--- --- ---
--- --- ---
loses:
count = 13
□-- --- ---
--- --- ---
--- --- ---
count = 11
--- --- ---
--- □-- ---
--- --- ---
count = 11
--- □-- ---
--- --- ---
--- --- ---
(対称な局面は除外してある)
解析結果によると、初手は場所に拘らず小さな駒か大きな駒を置けば先手必勝となり、逆に中くらいの駒だとどこに置いても後手必勝になってしまうという興味深い結果が得られた。
さらに最短手順にするには小さな駒を辺に置くか、大きな駒を真ん中または端に置く事が必要だとわかった。
補足
もう少し踏み込んで解析したいところではあるが、実際に商品として販売されているゲームなので配慮が必要かと思い、必勝手順をそのまま載せるのではなくやや限定的な情報のみに留めた。
また内部的な話として、当初ミニマックス法を使用して解析しようとして1週間ほど浪費してしまったため、最初に適切な情報を念入りに調べておくという必要性を学んだ。